Cím:	Az elfeledett közép
Szerző(k):	Hargitai Sára ,  Unyi Tamás
Füzet:	2020/október, 386 - 394. oldal	PDF  |  MathML
Témakör(ök):	Matematika, Szakmai cikkek, Nevezetes egyenlőtlenségek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Bevezetés ,,Kezdetben vala a számtani, a mértani és a harmonikus közép$\text{...}$'' Némi módosítással idéztünk egy tanulmányból, amely a matematikai középértékekkel foglalkozik [13]. Valóban, ezeket a közepeket ‐ az ókori görög matematika arányelméletének keretein belül, arányokkal kifejezve ‐ már Püthagorasz is ismerte, sőt a történeti források szerint babilóniai tanulmányútja során tett szert erre a tudásra. Matematikai vonatkozású régészeti leletek is arra utalnak, hogy ezeket a közepeket már a babilóniai tudósok is használták, Krisztus előtt csaknem kétezer évvel [9]. Püthagorasz egyik későbbi követője, Arkhütasz olyan megfogalmazást adott ezekre a közepekre, amelyből kiindulva további középértékekhez vezető eljárást dolgoztak ki a pitagoreusok. Az így kapott közepeket ezért pitagoraszi vagy ,,görög'' közepeknek nevezzük [2], [4], [7], [9], [10], [16], [21], [22]. Ezek közé tartozik a kontraharmonikus közép is, amely azonban ‐ egyszerűsége ellenére ‐ mára sajnos méltatlanul elfeledetté és mellőzötté vált, legalábbis középiskolai szinten. Tanulmányunkban a kontraharmonikus közép tulajdonságaival, összefüggéseivel, előfordulásával foglalkozunk, néhány saját eredménnyel is gazdagítva a témát. A dolgozatban szereplő állítások nagy részét ‐ terjedelmi okok miatt ‐ nem bizonyítjuk; a bizonyítások feladatát F-fel jelölve gyakorlásként az Olvasóra bízzuk.   A legismertebb közepek és a kontraharmonikus közép Mit is értünk két pozitív valós szám középértéke alatt? Azt az értéket, amely a két szám közé esik. Pontosabban: matematikai középnek nevezünk egy, a pozitív valós számpárok halmazán értelmezett kétváltozós, folytonos függvényt, melynek bármely helyettesítési értéke az adott számpár tagjai közé esik (megengedve a valamelyik taggal való esetleges egyenlőséget is). A középérték fogalma sok esetben könnyen kiterjeszthető több számra is, továbbá súlyozásra is van lehetőség. A középiskolában tárgyalt legismertebb közepeket az alábbi táblázatban tüntettük fel.1   ${\displaystyle \begin{array}{|ccc|}\hline \hfill {\displaystyle \text{<span style="font-weight: bold;">Közép neve</span>}}\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">Képlet</span>}}\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">Jelölés</span> }}\hfill \\ \hfill {\displaystyle \text{számtani (aritmetikai)}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mstyle displaystyle="true"><mrow><mfrac><mrow><mi>a</mi><mo stretchy="false">+</mo><mi>b</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></mstyle></math> <math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mspace backround="\#000" height="18pt" depth="10pt"></mspace></mphantom></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math> }}\hfill \\ \hfill {\displaystyle \text{mértani (geometriai)}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mroot><mrow><mi>a</mi><mo>⋅</mo><mi>b</mi></mrow><mrow></mrow></mroot></mrow></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mspace backround="\#000" height="12pt" depth="4pt"></mspace></mphantom></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>G</mi></math> }}\hfill \\ \hfill {\displaystyle \text{harmonikus}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mstyle displaystyle="true"><mrow><mfrac><mrow><mn>2</mn></mrow><mrow><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mi>a</mi></mrow></mfrac></mrow><mo stretchy="false">+</mo><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mi>b</mi></mrow></mfrac></mrow></mrow></mfrac></mrow></mstyle><mo stretchy="false">=</mo><mstyle displaystyle="true"><mrow><mfrac><mrow><mn>2</mn><mi>a</mi><mi>b</mi></mrow><mrow><mi>a</mi><mo stretchy="false">+</mo><mi>b</mi></mrow></mfrac></mrow></mstyle></math> <math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mspace backround="\#000" height="18pt" depth="16pt"></mspace></mphantom></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>H</mi></math> }}\hfill \\ \hfill {\displaystyle \text{négyzetes (kvadratikus)<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow></mrow><mrow><mi>*</mi></mrow></msup></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mroot><mrow><mstyle displaystyle="true"><mrow><mfrac><mrow><mrow><msup><mrow><mi>a</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo stretchy="false">+</mo><mrow><msup><mrow><mi>b</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></mstyle></mrow><mrow></mrow></mroot></mrow></math> <math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mspace backround="\#000" height="20pt" depth="10pt"></mspace></mphantom></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Q</mi></math> }}\hfill \\ \hline\end{array}}$   Fordítsuk figyelmünket most arra a bizonyos elfeledett középre. Két pozitív valós szám ($a$ és $b)$ kontraharmonikus közepe: $\begin{array}{c}{\displaystyle C\left(a\mathrm{,}b\right)=\frac{a^2+b^2}{a+b}\mathrm{.}}\end{array}$ Ez valójában egy $a$-val, illetve $b$-vel súlyozott számtani közép (,,önsúlyozott'' közép) [12], de úgy is tekinthetjük, hogy $a^2$ és $b^2$ számtani közepének, illetve $a$ és $b$ számtani közepének a hányadosa. A definícióból könnyen levezethető a kontraharmonikus közép néhány alapvető tulajdonsága. (F) $a)$ $C\left(a\mathrm{,}b\right)$ jogosult a középérték névre, mivel minden $a\le b$ esetén: $\begin{array}{c}{\displaystyle a\le C\left(a\mathrm{,}b\right)\le b\mathrm{.}}\end{array}$ $b)$ $C\left(a\mathrm{,}b\right)$ szigorú (vagy diagonális) közép, ami azt jelenti, hogy az előbbi egyenlőtlenségek szigorúakká válnak, ha $a$ különbözik $b$-től, de ha $a$ és $b$ megegyezik, akkor $C\left(a\mathrm{,}b\right)$ is egyenlő ezekkel. $c)$ $C\left(a\mathrm{,}b\right)$ szimmetrikus közép, azaz a képletében $a$ és $b$ szerepe felcserélhető: $\begin{array}{c}{\displaystyle C\left(a\mathrm{,}b\right)=C\left(b\mathrm{,}a\right)\mathrm{.}}\end{array}$ $d)$ $C\left(a\mathrm{,}b\right)$ homogén közép, ami alatt azt értjük, hogy tetszőleges pozitív valós $\lambda$ esetén: $\begin{array}{c}{\displaystyle C\left(\lambda a\mathrm{,}\lambda b\right)=\lambda \cdot C\left(a\mathrm{,}b\right)\mathrm{.}}\end{array}$ A homogenitás jelentősége többek között abban áll, hogy a két szám közös tényezője ,,kiemelhető'' a közép elé. A következőkben egy olyan módszert mutatunk be, amely hatékonyan alkalmazható a közepek tulajdonságainak, illetve kapcsolatainak a vizsgálatára, ennek ellenére ritkán találkozunk ezzel a szakirodalomban [5], [11]. Felhasználva a kontraharmonikus közép homogenitását, végezzük el az alábbi átalakítást: $\begin{array}{c}{\displaystyle C\left(a\mathrm{,}b\right)=b\cdot C\left(\frac{a}{b}\mathrm{,1}\right)=b\cdot C\left(x\mathrm{,1}\right)\mathrm{,}\text{ahol}x=\frac{a}{b};x>0.}\end{array}$ Ennek alapján $b$ lerögzítésével a kontraharmonikus középhez hozzárendelhetünk egy egyváltozós függvényt, amit karakterisztikus függvénynek nevezünk. Tehát: $\begin{array}{c}{\displaystyle f_C\left(x\right)=C\left(x\mathrm{,1}\right)=\frac{x^2+1}{x+1}\mathrm{.}}\end{array}$ A karakterisztikus függvény segítségével úgy igazolhatjuk a középérték-tulajdonságot, hogy belátjuk: ${\displaystyle \begin{array}{cccccc}\hfill {\displaystyle x}& {\displaystyle \le f_C\left(x\right)\le \mathrm{1,}}\hfill & {\displaystyle \text{ha }a}\hfill & \hfill {\displaystyle \le b\mathrm{,}}& {\displaystyle \text{azaz ha }0}\hfill & {\displaystyle <x\le \mathrm{1,}}\hfill \\ \hfill {\displaystyle 1}& {\displaystyle \le f_C\left(x\right)\le x\mathrm{,}}\hfill & {\displaystyle \text{ha }a}\hfill & \hfill {\displaystyle \ge b\mathrm{,}}& {\displaystyle \text{azaz ha }x}\hfill & {\displaystyle \ge 1.}\hfill \end{array}}$ Ez azt jelenti, hogy $f_C\left(x\right)$ grafikonjának az $y=1$ és az $y=x$ egyenletű egyenesek által határolt tartományban kell húzódnia. Amint az az 1. ábrán látható (és természetesen számításokkal is egyszerűen alátámasztható), $f_C\left(x\right)$ grafikonja valóban a ,,megengedett'' tartományban van. 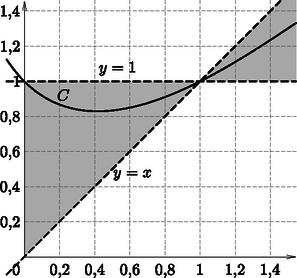    1. ábra   A grafikonon az is megfigyelhető, hogy a kontraharmonikus közép karakterisztikus függvénye a $\left]0;1\right]$ intervallumban nem monoton, hanem szélsőértéke, mégpedig minimuma van. A többféleképpen is elvégezhető pontos elemzés szerint a minimum helye: $x=\sqrt[]{2}-1$. (F) A karakterisztikus függvény nem kölcsönösen egyértelmű voltából a kontraharmonikus közép különleges tulajdonsága következik: ha rögzítjük egy számpár nagyobbik tagját, akkor a kisebbik tag két különböző értéke esetén is ugyanazt a kontraharmonikus közepet kaphatjuk. Pl.: $C\left(\mathrm{2,6}\right)=C\left(\mathrm{3,6}\right)=5$. A jól ismert közepek karakterisztikus függvényét hasonlóképpen határozhatjuk meg (2. ábra). (F) 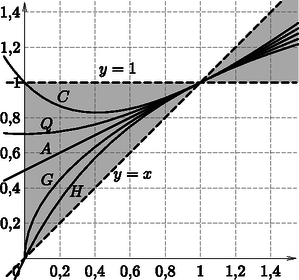    2. ábra   A grafikonok tanúsága és az elemzés szerint a számtani, mértani, harmonikus és négyzetes közép karakterisztikus függvénye szigorúan monoton növő, tehát ezeknél a közepeknél nem tapasztalható az a ,,kettősség'', amelyet a kontraharmonikus középnél láttunk. Az ilyen középértékeket izotonnak nevezzük [2]. A kontraharmonikus középnek a többi középétől eltérő tulajdonsága tehát az, hogy nem izoton, hiszen a karakterisztikus függvénye nem monoton. Az ábráról ugyanakkor a közepek sorrendje is leolvasható, és így adódik a nevezetes egyenlőtlenség-láncolat, amelybe most már a kontraharmonikus közép is beilleszthető: $\begin{array}{c}{\displaystyle H\le G\le A\le Q\le C\mathrm{,}}\end{array}$ ahol az egyenlőségek akkor és csak akkor teljesülnek, ha $a=b$. (F)   A derékszögű érintőtrapéz A következőkben bemutatjuk a kontraharmonikus közép egy geometriai előfordulását, miközben rávilágítunk más közepekkel való összefüggéseire és a pitagoraszi számhármasokkal való kapcsolatára. Mindezt egy tétel kimondásának és bizonyításának keretén belül tesszük.   Tétel. I. Ha $a$ és $b$ különböző pozitív egész számok, és $C\left(a\mathrm{,}b\right)$ (vagyis a kontraharmonikus közepük) is egész, akkor $C\left(a\mathrm{,}b\right)$ előáll egy pitagoraszi számhármas legnagyobb tagjaként. II. Ha $\left(x\mathrm{,}y\mathrm{,}z\right)$ pitagoraszi számhármas, akkor létezik két különböző pozitív egész szám, melyeknek kontraharmonikus közepe éppen a számhármas legnagyobb tagja (azaz $z$, amely szintén egész).   Bizonyítás. Tekintsünk egy derékszögű érintőtrapézt (3. ábra), melynek alapjai $a$, illetve $b$ hosszúak ($a<b)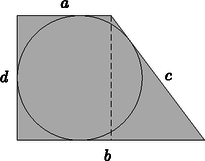$.     3. ábra   Hogy $a$ és $b$ ismeretében kifejezhessük a szárak hosszát ($c$-t és $d$-t), írjuk fel az érintőnégyszögek tételét és a Pitagorasz-tételt: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle c+d}& {\displaystyle =a+b\mathrm{,}}\hfill \\ \hfill {\displaystyle d^2+{\left(b-a\right)}^2}& {\displaystyle =c^2\mathrm{.}}\hfill \end{array}}$ Az egyenletrendszer megoldásával az alábbi eredményre jutunk: $\begin{array}{c}{\displaystyle c=\frac{a^2+b^2}{a+b}\mathrm{,}d=\frac{2ab}{a+b}}\end{array}$ A merőleges szár hosszára tehát az alapok hosszának a harmonikus közepét, a másik szár hosszára pedig a kontraharmonikus közepét kapjuk. Ezen a ponton tegyünk egy kis kitérőt. Azonnal láthatjuk, hogy két különböző számnak a kontraharmonikus közepe nagyobb, mint a harmonikus közepe, amit algebrai úton is igazolhatunk. Írjuk fel újra az érintőnégyszögek tételét, most már a kapott eredményekkel. $\begin{array}{c}{\displaystyle H+C=a+b\mathrm{.}}\end{array}$ 2-vel való osztás után kapjuk a számtani közép definíciója alapján: $\begin{array}{c}{\displaystyle A\left(H\mathrm{,}C\right)=A\left(a\mathrm{,}b\right)\mathrm{.}}\end{array}$ Vagyis mindegy, hogy két szám harmonikus és kontraharmonikus közepének vesszük a számtani közepét, vagy magának az eredeti két számnak a számtani közepét. Erre azt mondjuk, hogy a számtani közép invariáns a harmonikus és a kontraharmonikus középre nézve. Szokás úgy is fogalmazni, hogy a harmonikus és a kontraharmonikus közép egymásnak a komplementere a számtani középre vonatkozóan [20]. Középiskolai szóhasználattal: két tetszőleges pozitív valós szám harmonikus, számtani és kontraharmonikus közepe egy számtani sorozat egymást követő tagjai. Az ábra tehát magában rejt egy közepek közötti, invariancia jellegű összefüggést, amely egyúttal magyarázatot ad a kontraharmonikus elnevezésre is. Térjünk vissza a tétel bizonyítására. Tegyük fel, hogy $a$ és $b$ egész számok, és a kontraharmonikus közepük is egész. Válasszunk le a derékszögű érintőtrapézból egy derékszögű háromszöget. Ennek oldalhosszai: $b-a$, $d$, $c$. Ezek azonban a feltételek miatt mind egész számok (hiszen $c=C\left(a\mathrm{,}b\right)$, illetve $d=a+b-c$ az érintőnégyszögek tételéből). Tehát kaptunk egy pitagoraszi számhármast, melynek legnagyobb tagja éppen $C\left(a\mathrm{,}b\right)$. Ezzel bebizonyítottuk a tétel I. részét. Induljunk ki most egy $\left(x\mathrm{,}y\mathrm{,}z\right)$ pitagoraszi számhármasból, azaz három olyan pozitív egész számból, melyek egy derékszögű háromszög oldalhosszai. Egészítsük ki ezt a háromszöget derékszögű érintőtrapézzá (4. ábra). (A szerkesztés nem bonyolult: az egyik hegyesszögű csúcsból kiinduló szögfelezőnek, illetve a csúccsal szemközti befogó és az átfogó felezőpontját összekötő középvonalnak a metszéspontjaként kapjuk a szerkesztendő trapézba írható kör középpontját; a kör megrajzolása után pedig már könnyű megszerkeszteni a trapézt.)     4. ábra   A kapott derékszögű érintőtrapéz hosszabbik száráról tudjuk, hogy annak hossza egyrészt az alapok hosszának ($a$-nak és $b$-nek) a kontraharmonikus közepe, másrészt egész szám, hiszen a pitagoraszi számhármas legnagyobb tagja (a derékszögű háromszög átfogójának a hossza). Már csak azt kell belátni, hogy az alapok hossza is egész szám. Az ábra alapján írjunk fel két összefüggést $a$ és $b$ között: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a+b}& {\displaystyle =x+z\mathrm{,}}\hfill \\ \hfill {\displaystyle b-a}& {\displaystyle =y\mathrm{.}}\hfill \end{array}}$ Ebből kapjuk: $\begin{array}{c}{\displaystyle a=\frac{x-y+z}{2}\mathrm{,}b=\frac{x+y+z}{2}\mathrm{.}}\end{array}$ $i)$ Foglalkozzunk először egy ún. primitív pitagoraszi számhármassal, amelyben a tagoknak nincs 1-nél nagyobb közös osztója. Ismeretes, hogy ebben az esetben a tagok a következő módon fejezhetők ki az $m$ és $n$ pozitív egész számokkal [17]: $\begin{array}{c}{\displaystyle x=2mn\mathrm{,}y=m^2-n^2\mathrm{,}z=m^2+n^2}\end{array}$ ($m>n$, továbbá $m$ és $n$ relatív prímek és különböző paritásúak; $x$ jelöli a számhármas egyetlen páros tagját.) Behelyettesítés és rendezés után adódik: $\begin{array}{c}{\displaystyle a=n\cdot \left(m+n\right)\mathrm{,}b=m\cdot \left(m+n\right)\mathrm{.}}\end{array}$ Tehát az alapok hossza valóban egész szám. $ii)$ Ha a pitagoraszi számhármas nem primitív, akkor a tagok legnagyobb közös osztója nagyobb 1-nél. Jelöljük ezt az egész számot $k$-val. Ha mindhárom tagot $k$-val osztjuk, akkor primitív pitagoraszi számhármashoz jutunk, így az előzőek szerint egész számokat kapunk az alapok hosszára. Ezeket $k$-val megszorozva adódnak az eredeti számhármashoz tartozó alaphosszúságok, amelyek természetesen szintén egész számok. Ez teszi teljessé a tétel II. részének a bizonyítását. A tétel kimondása Pahikkala nevéhez fűződik, aki az iménti, geometriai hátterű bizonyítás helyett tisztán algebrai módszert alkalmazott [18]. Megjegyzés. A szerkesztésből kitűnik, hogy a derékszögű háromszöget a másik befogójának az irányában is kiegészíthetjük derékszögű érintőtrapézzá (5. ábra). 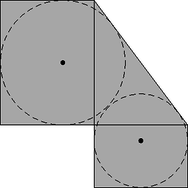    5. ábra   Ez annak felel meg, hogy az alapok hosszának a képletében $x$ és $y$ szerepe felcserélődik: $\begin{array}{c}{\displaystyle a\text{'}=\frac{y-x+z}{2}\mathrm{,}b\text{'}=\frac{x+y+z}{2}\mathrm{.}}\end{array}$ Mint látható, a hosszabbik alap hosszára ugyanazt az értéket kapjuk, a rövidebbik alapéra azonban nem: $\begin{array}{c}{\displaystyle a\text{'}=z-a\mathrm{,}b\text{'}=b\mathrm{.}}\end{array}$ Eközben a trapéz hosszabbik szára ‐ azaz a kiindulási derékszögű háromszög átfogója ‐ nem változik. Mindez összhangban van a kontraharmonikus közép nem izoton voltával, azaz azzal a korábban megállapított ténnyel, hogy ha rögzítjük egy számpár nagyobbik tagját, akkor a kisebbik tag két különböző értéke esetén is ugyanaz a kontraharmonikus közép adódik [18]: $\begin{array}{c}{\displaystyle C\left(a\mathrm{,}b\right)=C\left(a\text{'}\mathrm{,}b\right)\mathrm{,}a+a\text{'}=C\mathrm{.}}\end{array}$   A kontraharmonikus közép előfordulásai $a)$ Bizonyára sokan tudják, hogy a trapéz alapjaival párhuzamos szakaszok (az ún. húrok) némelyikének a hossza mögött a legismertebb közepek rejtőznek [4], [6], [20]. Kevésbé közismert azonban, hogy a kontraharmonikus közép is fellelhető a trapézban. Például ha találunk egy olyan pontot a trapézon belül, amelyet egy-egy alap végpontjaival összekötve a kapott háromszögek területe megegyezik, akkor az ezen a ponton áthaladó húr hossza az alapok hosszának a kontraharmonikus közepével lesz egyenlő (6. ábra) [23]. (Könnyen belátható, hogy a szóban forgó húr összes pontja rendelkezik az elsőként megtalált pontéhoz hasonló tulajdonsággal.) (F) 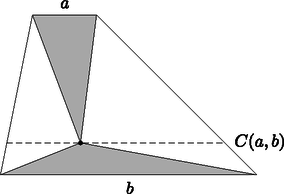    6. ábra   $b)$ Keressük meg egy érintőtrapéznak azt a húrját, amely két egyenlő kerületű kisebb trapézra bontja az eredeti trapézt (azaz amely megfelezi az eredeti trapéz kerületét). Ennek a húrnak a hossza egyenlő az alapok hosszának a kontraharmonikus közepével. (F) $c)$ A derékszögű háromszög átfogójához, illetve az egyik befogóhoz írt kör sugarának kontraharmonikus közepére éppen az átfogó hosszát kapjuk. Az a tény, hogy az állításban bármelyik befogó szerepelhet, a kontraharmonikus közép nem izoton voltára utal. (Az átfogóhoz, illetve az egyik befogóhoz írt kör sugarának harmonikus közepe pedig az adott befogó hosszával egyenlő.) (F) $d)$ Tekintsünk egy egyenes csonka kúpot, amelyről tudjuk, hogy az alaplap és a fedőlap területének az összege egyenlő a palást területével. Ekkor az alkotó hossza megegyezik az alaplap és a fedőlap sugarának a kontraharmonikus közepével. (A csonka kúp magassága pedig a sugarak harmonikus közepével egyenlő.) (F) $e)$ Tekintsük a $g:{\text{R}}^{+}\to {\text{R}}^{+}$, $g\left(x\right)=1/x$ függvényt (7. ábra). 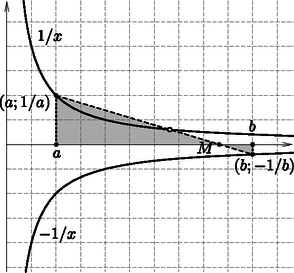    7. ábra   Tükrözzük a függvény grafikonját az $x$-tengelyre, és jelöljünk ki a tengelyen egy tetszőleges $a$-t és $b$-t $\left(a<b\right)$. Kössük össze az $\left(a;1/a\right)$ és a $\left(b;-1/b\right)$ pontokat (Moskovitz‐Mays-féle eljárás [14], [15]). Az összekötő egyenes egy $a$ és $b$ közötti $M$ pontban metszi az $x$-tengelyt. $M$ meghatározásához vegyük észre, hogy az ábrán látható derékszögű háromszögek hasonlók, és írjuk fel az egymásnak megfeleltethető befogóhosszak arányának egyenlőségét: $\begin{array}{c}{\displaystyle \frac{M-a}{b-M}=\frac{\frac{1}{a}}{\frac{1}{b}}=\frac{b}{a}\mathrm{.}}\end{array}$ Rendezés után kapjuk: $\begin{array}{c}{\displaystyle M\left(a\mathrm{,}b\right)=\frac{a^2+b^2}{a+b}\mathrm{.}}\end{array}$ Vagyis ezzel az eljárással $a$ és $b$ kontraharmonikus közepéhez jutottunk. Megfigyelhetjük, hogy a két szélső pontot összekötő egyenes még egy helyen metszi a függvény grafikonját. Ez azt jelenti, hogy a nagyobbik szám ($b$) rögzítésével a kisebbik szám ($a$) két különböző értéke mellett is ugyanazt a kontraharmonikus közepet kapjuk, ami ismét a kontraharmonikus közép nem izoton voltát jelzi. $f)$ Számadatok átlagáról legtöbbször a számtani közép jut az eszünkbe, pedig az átlag meghatározása erősen függ attól, hogy mit tartunk szem előtt az adathalmaz és az azt ,,képviselő'' átlagérték viszonyában. A számtani közepet akkor kapjuk átlagul, ha arra törekszünk, hogy az adatoknak az átlagtól való négyzetes eltérése összességében a lehető legkisebb legyen (ekkor a szórás is minimális). $\begin{array}{c}{\displaystyle \sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2=\text{min.}\iff \overline{x}=A\left(x_1\mathrm{,}\text{...}\mathrm{,}{x}_n\right)\mathrm{.}}\end{array}$ Ha azonban azt akarjuk, hogy az adatoknak az átlagtól való relatív (tehát az átlaghoz viszonyított) négyzetes eltérése legyen összességében minimális, akkor a kontraharmonikus közép adódik átlagnak [1]. $\begin{array}{c}{\displaystyle \sum _{i=1}^n{\left(\frac{x_i-\overline{x}}{\overline{x}}\right)}^2=\text{min.}\iff \overline{x}=C\left(x_1\mathrm{,}\text{...}\mathrm{,}{x}_n\right)\mathrm{.}}\end{array}$ $g)$ Érdekes, hogy a kontraharmonikus közép (és nemcsak az) még a zenében is felbukkan. Két hang magasságbeli különbségét a hangközzel jellemezzük, ez pedig a két hang frekvenciájának aránya. Tekintsünk egy alaphangot (pl. C), ennek oktávját (C'), továbbá a következő hangközöket: kvart (F), kvint (G), nagy szext (A). Ha az alaphang frekvenciáját egységnyinek vesszük, akkor az oktáv frekvenciája 2, a kvarté $4/3$, a kvinté $3/2$, a nagy szexté pedig $5/3$ egység, legalábbis az ún. természetes (vagy diatonikus) dúr skálán [3]. Látható, hogy az alaphang és az oktáv frekvenciájának számtani közepe a kvint frekvenciájával, harmonikus közepe pedig a kvart frekvenciájával egyezik meg, amint az már a pitagoreusok számára is ismert volt (persze nem a frekvenciákkal megfogalmazva, hanem a rezgésbe hozott, és így a megfelelő hangot kibocsátó húr hosszának a felhasználásával) [8], [9], [19], [22]. Ha azonban a kontraharmonikus közép is szerepel az eszköztárunkban, észrevehetjük, hogy a nagy szext frekvenciája éppen ennek a középnek felel meg.   Kitekintés A cikkbeli táblázatban szereplő, legismertebb közepek valójában egy nagyobb családnak, az ún. hatványközepek családjának a tagjai [2], [4], [20]. A kontraharmonikus közép nem tartozik ebbe a családba. Az viszont mind a hatványközepekről, mind a kontraharmonikus középről elmondható, hogy a számtani középre vezethetők vissza. Jogosan vetődhet fel a kérdés a kontraharmonikus közép tényleges hovatartozását illetően. A választ jelen tanulmányunk folytatása foglalja majd magába.   Felhasznált és ajánlott szakirodalom [1] Beckenbach, E. F.: A class of mean value functions. The American Mathematical Monthly, 57. No. 1. (1950), 1‐6. [2] Borwein, J. M. & Borwein, P. B.: Pi and the AGM. A study in analytic number theory and computational complexity. John Wiley, New York, 1987. [3] Budó Ágoston: Kísérleti fizika I. Tankönyvkiadó, Budapest, 1972. [4] Bullen, P. S.: Handbook of means and their inequalities. Springer Science + Business Media, Dordrecht, 2003. [5] Chen, H.: Means generated by an integral. Mathematics Magazine, 78. No. 5. (2005), 397‐399. [6] Eves, H.: Means appearing in geometric figures. Mathematics Magazine, 76. No. 4. (2003), 292‐294. [7] Faradj, M. K.: Which mean do you mean? An exposition on means. http://digitalcommons.lsu.edu/gradschool_theses (Letöltés ideje: 2017. 11. 15.). [8] Hámori Miklós: Arányok és talányok. Typotex Kft., Budapest, 1994. [9] Hischer, H.: Viertausend Jahre Mittelwertbildung. mathematica didactica, 25. No. 2. (2002), 3‐51. [10] Kovács Veronika & Petz Dénes: Számtani közép, mértani közép, meg ilyenek. Középiskolai Matematikai és Fizikai Lapok, 56. No. 3. (2006), 130‐136. [11] Lambert, A. & Herget, W.: Mächtig viel Mittelmaß in Mittelwert-Familien. Der Mathematikunterricht, 50. No. 5. (2004), 55‐66. [12] Lann, A. & Falk, R.: Ein etwas vernachlässigter Mittelwert. Stochastik in der Schule, 27. No. 1. (2007), 2‐4. [13] Leach, E. B. & Sholander, M. C.: Extended mean values. The American Mathematical Monthly, 85. No. 2. (1978), 84‐90. [14] Mays, M. E.: Functions which parametrize means. The American Mathematical Monthly, 90. No. 10. (1983), 677‐683. [15] Moskovitz, D.: An alignment chart for various means. The American Mathematical Monthly, 40. No. 10. (1933), 592‐596. [16] ifj. Orbán György: A püthagoraszi középarányosok jelentős tulajdonságai és szerepük az építészetben. XV. Műszaki Tudományos Ülésszak, Kolozsvár, 2014, 161‐172. [17] Ore, O.: Bevezetés a számelmélet világába. Gondolat, Budapest, 1977. [18] Pahikkala, J.: On contraharmonic mean and Pythagorean triples. Elemente der Mathematik, 65. No. 2. (2010), 62‐67. [19] Sain Márton: Nincs királyi út! Gondolat, Budapest, 1986. [20] Szikszai József: A hatványközepek. Tankönyvkiadó, Budapest, 1987. [21] Toader, Gh. & Toader, S.: Greek means and the arithmetic-geometric mean. RGMIA Monographs, Victoria University, 2005. [22] Wassell, S. R.: Rediscovering a family of means. The Mathematical Intelligencer, 24. No. 2. (2002), 58‐65. [23] Witkowski, A.: Gini and Stolarsky means in geometric problems. Conference on Inequalities and Applications, Hajdúszoboszló, 2010.   ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{<span style="font-weight: bold;">Hargitai Sára, Unyi Tamás</span><br> Gödöllői Református Líceum}}\hfill \end{array}}$ 1A négyzetes közép valójában nem tartozik a pitagoraszi közepek családjába, csak az ismertsége miatt szerepel a táblázatban.