|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A 2020. évi Kunfalvi Rezső Olimpiai Válogatóverseny
elméleti feladatainak megoldása F1. A golyó csak úgy érkezhet a gödör sarkába, ha előtte a gödör függőleges oldalain páratlan számszor visszapattan. Minden visszaverődésnél a kis test sebességének vízszintes komponense előjelet vált, függőleges komponense pedig változatlan marad. A pattogó golyó pályáját a függőleges falakra való tükrözéssel ,,ki lehet hajtogatni'', és így töréspontok nélküli parabolát kapunk. Nyilvánvaló, hogy közelebbi pontba kisebb kezdősebességgel eljuttatható a golyó, tehát az optimális (kihajtogatott) pálya esetén a golyó csak egyszer pattan meg. Most már csak az a kérdés, hogy az eldobás helyétől távolabbi falon hol legyen a pattanási pont.
 1. ábra 1. ábra
Paraméterezzük a feladatot! Legyen m a gödör távolabbi falának távolsága az ponttól, m a gödör szélessége, m a gödör mélysége. Ezeken kívül használni fogjuk még az m távolságot is. Jelölje és a gödör ponthoz közelebbi, illetve távolabbi felső sarkát, pedig a pontnak a gödör távolabbi falára vonatkozó tükörképét (1. ábra). A kihajtogatott pálya tehát egy olyan parabola, amely átmegy az és pontokon.
Az és pontokat összekötő lehetséges parabolák közül csak azokat választhatjuk, amelyek ,,beesnek'' a gödörbe, azaz a talaj szintjét a szakaszon metszik. Szemléletesen látható, hogy ezek közül a pályák közül a legmagasabb, parabolához tartozik a legkisebb kezdősebesség, míg a leglaposabb, parabolához a legnagyobb kezdősebesség. (Itt figyelembe vettük azt a tényt is, hogy a feladat adatai alapján lapos, -nál jóval kisebb szögben induló hajításokról van szó.)
*
Megjegyzés. Az intuíciónkat számolással is igazolhatjuk. Ha a hajítás kezdősebessége , az indítás hajlásszöge , akkor az és pontok közötti vízszintes () és függőleges () elmozdulásokra a következőket írhatjuk fel: amiből a mozgás idejének kiküszöbölése után az alábbi kifejezést kapjuk -re: | | () |
Ahhoz, hogy kiderüljön, hogyan változik nagysága az szög kis megváltoztatásakor, vizsgáljuk meg a tört nevezőjének szög szerinti deriváltját: | |
A távolságadatok behelyettesítésével könnyen ellenőrizhető, hogy ez a derivált és annál kisebb szögekre biztosan pozitív, azaz ,,lapos'' hajítási szögek esetén a pont eltalálásához szükséges sebesség annál kisebb, minél nagyobb az szög értéke. A gödörbe beleeső golyó lehetséges pályái közül az 1. ábrán látható ponton átmenő parabolához tartozik a legkisebb szög, míg értéke a ponton átmenő pálya esetén a legnagyobb. Tehát az optimális pálya a gödör távolabbi függőleges falát a legfelső, pontban találja el, majd egy pattanás után a kis test a pontba érkezik.
*
A kinematikai egyenletekből kiindulva felírhatjuk az optimális pálya szakaszán a golyó vízszintes elmozdulását az szög és a kezdősebesség segítségével: A megjegyzésben szereplő egyenletből beírva ide -et megkapjuk a hajítási szöget: | |
Ezt az eredményt visszaírva a egyenletbe a következő kifejezéshez jutunk: | |
Az adatokat behelyettesítve végül megkapjuk a sebesség számszerű értékét:
F2. Mivel a szupravezető belsejébe a mágneses tér nem hatolhat be, az indukcióvonalak folytonosságából következően a mágneses indukcióvektornak mindenhol érintőirányúnak kell lennie a cső külső és belső felülete mentén. A feladatunk az, hogy a határfeltételt kielégítő (felületi) árameloszlást megtaláljuk.
Az ilyen, ún. peremérték-problémákat középiskolás szinten a tükrözés módszerével szoktuk megoldani. Ennek lényege, hogy egy zárt tartomány peremén elhelyezkedő áram- vagy töltéseloszlás hatását a tartományon kívül található, megfelelően megválasztott erősségű és helyzetű ,,tüköráramokkal'' vagy ,,tükörtöltésekkel'' helyettesítjük. Ez az eljárás csak néhány speciális geometriájú felület (pl. síkok, gömb vagy henger) esetén működik, de most éppen ilyennel van dolgunk. Próbáljuk hát a szupravezető cső falában folyó áramok hatását egy, a csövön kívül elhelyezkedő, képzeletbeli, áramjárta egyenes vezetővel leírni!
Könnyen látható, hogy a ,,tüköráram'' a cső belsejében lévő vezetékben folyó valódi árammal ellentétes irányú, ellenkező esetben a mágneses indukcióvektor sugárirányú komponense nem tűnhetne el a cső fala mentén. A szimmetria miatt a tüköráram a cső tengelye és a valódi áramvezető által meghatározott síkban helyezkedik el. Jelöljük (általánosan) a valódi vezetőnek, illetve a tüköráramnak a cső tengelyétől mért távolságát rendre -vel és -szel (az ennek megfelelő vektorok pedig legyenek és ). A tüköráram egyelőre ismeretlen erősségét jelöljük -vel ().
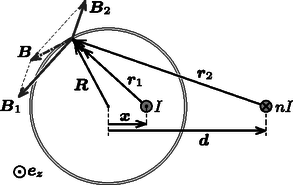 2. ábra 2. ábra
Vizsgáljuk a szupravezető cső szimmetriatengelyre merőleges síkmetszetét, és írjuk fel belül a mágneses indukcióvektort az ábra jelöléseivel a cső tengelyéhez képest vektorral jellemezhető pontban ()! A valódi áramvezető és a tüköráram által keltett indukciójárulékok vektoros alakban: | |
ahol és a vezetékektől a vizsgált pontba mutató vektorok, pedig a valódi vezetékben folyó árammal azonos irányú egységvektor. Azt szeretnénk elérni, hogy az eredő indukcióvektor (ami és vektori összege) érintőirányú legyen, amit matematikailag így fejezhetünk ki: Ebbe behelyettesítve és korábbi kifejezését, majd egyszerűsítés után: | |
A vegyes szorzatra vonatkozó azonosságot felhasználva: | |
A szögletes zárójelben álló mindkét tag párhuzamos az vektorral, ezért a skaláris szorzat csak úgy lehet zérus, ha a zárójeles mennyiség eltűnik. Fejezzük ki az és vektorokat -szel és -vel! Ezzel a következő feltételt kapjuk: | |
A zárójeleket felbontva, majd felhasználásával: Az vektor minden értékére ez csak úgy lehetséges, ha a szögletes zárójelben álló vektor nullvektor. Mivel és egyirányú vektorok, ezért ennek feltétele: Szorozzunk be a nevezőkkel, és fejtsük ki az abszolútérték-négyzeteket: | |
Átrendezve: | |
Az egyenlet bal oldala nem függ az vektor irányától, míg a jobb oldal igen. Ez az egyenlőség csak úgy állhat fenn tetszőleges iránya esetén, ha , azaz az egyenlet mindkét oldala nulla. Ez azt jelenti, hogy a ,,tükörvezetékben'' folyó áram ugyanakkora nagyságú, de ellentétes irányú, mint a valódi vezetőben folyó áram.
Az helyettesítéssel rövid számolás után végül a következő eredményt kapjuk a tükörvezeték helyzetére: azaz esetén .
A cső belsejében a mágneses mezőt a valódi és a ,,tükörvezeték'' által keltett terek szuperpozíciójaként számolhatjuk. Az egyenes áramjárta vezetékre hosszegységenként ható Lorentz-erő kiszámításakor tehát a tükörvezeték által a valódi vezeték helyén keltett mágneses teret kell figyelembe vennünk: | |
Az erő taszító jellegű, a vezeték ,,igyekezne'' a szupravezető cső közepén elhelyezkedni.
A feladat síkbelisége miatt a cső belső és külső falán egyaránt tengelyirányú áram folyik. A belső felületen folyó áram vonalmenti sűrűségét az Ampre-féle gerjesztési törvénnyel határozhatjuk meg. Ehhez tekintsük az pont környékén a 3. ábrán látható, téglalap alakú zárt hurkot! 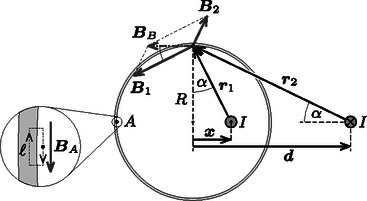 3. ábra 3. ábra
Ha a téglalap fallal párhuzamos oldala hosszúságú, akkor a gerjesztési törvény: hiszen a szupravezető anyagban a mágneses indukció értéke nulla. Ebből a vonalmenti áramsűrűség: és hasonló összefüggés igaz a cső belső falának bármely pontjára. Az pontbeli indukcióvektor nagysága szuperpozícióval könnyen számolható a tüköráram segítségével: | |
Az pont közelében tehát a cső belső falán a vonalmenti áramsűrűség:
A pontbeli indukcióvektor kiszámítása egy fokkal nehezebb, mert itt és nem párhuzamos irányú vektorok. A 3. ábrán látható szög segítségével az eredő indukcióvektor nagysága: | |
Felhasználva, hogy , : A megjelenő szögfüggvényeket a 3. ábra segítségével kifejezhetjük: Ebből végül a pontbeli indukció: valamint a vonalmenti áramsűrűség:
A cső belső felületén folyó árameloszlás önmagában elegendő ahhoz, hogy az indukcióvonalak behatolását a szupravezetőbe megakadályozza. Ennek az áramnak a teljes erőssége éppen , amint az könnyen belátható, ha az Ampre-törvényt a cső falában futó körre alkalmazzuk. Ennek az áramnak (a cső véges mérete miatt) valahol vissza is kell folynia, az pedig csak a cső külső felületén lehetséges. A külső felületen folyó áram eloszlásának olyannak kell lennie, hogy a cső falában az indukció továbbra is zérus maradjon. Ez úgy lehetséges, hogy a külső felületen az árameloszlás egyenletes, vonalmenti áramsűrűsége .
F3. A hatásfok definíciója alapján kifejezhetjük a belső Carnot-gép által felvett és leadott és hőteljesítményt az hatásfokkal és a gép által leadott mechanikai teljesítménnyel: | |
Fourier hővezetési törvénye a meleg és a hideg oldalon így írható: | |
A hőáramokra kapott korábbi formulák, illetve a hővezetési egyenletek felhasználásával kifejezhetjük a belső és hőmérsékletet a külső és hőmérséklettel, a hatásfokkal, valamint a leadott mechanikai teljesítménnyel:
A belső Carnot-gép hatásfokát a hőtartályok és hőmérsékletének ismeretében felírhatjuk, és így összefüggést kapunk és között: | |
ahonnan kifejezhető a keresett függvény: | |
Ahogy növeljük a gépből kivett mechanikai teljesítményt, nő a és hőáram is. Ha azonban ezek a hőáramok túl nagyok, akkor naggyá válik a külső és belső hőmérsékletek közötti illetve különbség, és a két belső hőmérséklet közel kerül egymáshoz, ami az hatásfok, illetve a teljesítmény csökkenéséhez vezet. Ez alapján látható, hogy van egy optimális hatásfok, ami mellett a leadott mechanikai teljesítmény maximális. A függvény maximumánál a derivált zérus, tehát | |
ahonnan a keresett maximumhely:
Érdekes, hogy az eredmény független a hővezetési tényezőktől, és ,,csupán'' a négyzetgyökjelben tér el a Carnot-gép hatásfokától.
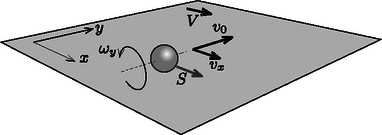
F4. Vezessünk be egy koordináta-rendszert, melynek tengelye a futószalag sebességével azonos irányú, tengelye pedig a labda kezdősebességének irányába mutat (4. ábra). Amikor a labda megérkezik a futószalagra, tömegközéppontjának irányú sebességkomponense zérus, irányú sebessége pedig a kezdeti érték: A labda kezdetben csak az iránnyal párhuzamos tengely körül forog, a szögsebesség-vektor komponense tehát nulla:
A futószalagra érve a labdára az állandó nagyságú csúszási súrlódási erő kezd hatni a futószalag sebességével megegyező irányban. A további mozgás során a súrlódási erő iránya mindig a labda legalsó pontjának a futószalaghoz viszonyított (relatív) sebességével ellentétes lesz.
 4. ábra 4. ábra
Látszik, hogy a súrlódási erő csak a sebesség komponensét és a szögsebességvektor komponensét változtatja meg, a tömegközéppont irányú sebességkomponensére és az tengellyel párhuzamos tengely körüli forgómozgásra nincs hatással. Ebből következik, hogy a labda legalsó pontjának futószalaghoz viszonyított relatív sebessége mindvégig irányú marad. Azaz a labdára ható csúszási súrlódási erőnek nem csak a nagysága, de az iránya is állandó!
A labda szalagra érkezésének időpillanatától számítva meghatározható, hogyan függ a tömegközéppont sebessége, valamint az szögsebesség az időtől: A labda ,,oldalazó'' csúszása közben és egyenletesen növekszik mindaddig, amíg elő nem áll a labda tiszta gördülése. Tiszta gördülésről akkor beszélhetünk, ha a labda futószalaggal érintkező pontjának nyugvó koordináta-rendszerben mért sebessége megegyezik a szalag sebességével. Matematikailag megfogalmazva: ahol a tiszta gördülés beálltának időpillanatát jelöli. A fenti egyenletből, valamint a szöggyorsulásra és a gyorsulásra kapott korábbi eredményekből kifejezhető: A feladat kitűzésében szerepel, hogy a súrlódási együttható (és emiatt is) igen nagy, így rövid időtartam. Vagyis a tiszta gördülés sokkal hamarabb beáll, mint amennyi idő alatt a labda átér a futószalag túlsó oldalára. A tiszta gördülés kialakulásától kezdve a labda tömegközéppontjának irányú komponense állandó lesz, értéke: A labda tehát az asztalhoz képest sebességgel egyenletesen mozog irányban, így mire átér a szalag túloldalára, utat tesz meg a szalaggal párhuzamosan, tehát ekkora mértékben tolódik el a pályája.
F5. Számozzuk meg a fémgömbhéjak főbb felületeit a 5. ábra bal oldala szerint! A feladatbeli elrendezés elektrosztatikus szempontból modellezhető az 5. ábra jobb oldalán látható rendszerrel. A töltések rendre az 1-4. felületeken levő töltéseknek feleltethetőek meg.
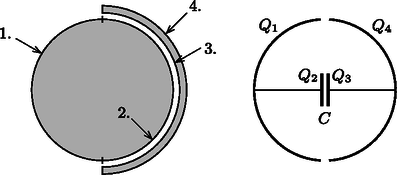 5. ábra 5. ábra
Tudjuk továbbá, hogy a feladatban szereplő félgömbhéjra összesen töltést juttattunk, tehát fennáll: A fémgömb össztöltése viszont nulla, amelyet a egyenlet fejez ki. A fenti egyenletrendszert megoldva a következő töltésértékeket kapjuk:
Az eddigi eredmények alapján kiszámíthatjuk az 5. ábra bal oldalán látható felületek töltéssűrűségét. A feladatkitűzésben szereplő fémgömb 1. és 2. felületeinek töltéssűrűsége: | |
Míg a félgömbhéj külső és belső felületének együttes töltéssűrűsége:
Ahhoz, hogy meghatározzuk, mekkora erővel hat egymásra a gömb és a félgömbhéj, meg kellene határoznunk, mekkora teret hozna létre a gömbfelületen levő töltéselrendeződés, ha a félgömbhéj nem lenne ott. Ebben az térben helyekedik el ugyanis a félgömbhéj, amelyre a térrel arányos nagyságú Coulomb-erő hat.
Az tér meghatározása érdekében vizsgáljuk meg a térerősséget félgömbhéj anyagának belsejében, vagyis a 3. és a 4. felület között! Ismert, hogy fémek belsejében az elektromos térerősség zérus, ez igaz a 3. és 4. felület közötti térrészben is. Itt a térerősséget három összetevő határozza meg az alábbi egyenlet szerint: ahol a fémgömb által keltett, egyelőre ismeretlen térerősség, a 3. felület által keltett tér, amely a 3. és 4. felületek közt sugárirányban kifelé mutat, továbbá a 4. felület járuléka, amely sugárirányban befelé mutat, így negatív előjellel kell figyelembe venni.
A fenti egyenletből a kérdéses térerősség kifejezhető: ahol felhasználtuk azt a Gauss-törvényből következő tényt, hogy az és térerősségek a 3. és 4. felület töltéssűrűségeivel arányosak. Mivel azonban , így . A polarizált fémgömb tehát nem hoz létre elektromos teret a félgömbhéj helyén, így a két test között nem lép fel erő!
F6. Gondolatban osszuk fel a bolygó légkörét koncentrikus, vékony gömbhéjakra! Vizsgáljuk a fénysugarat, ahogy beesési szög alatt belép az sugarú, vastagságú gömbhéjba (6. ábra).
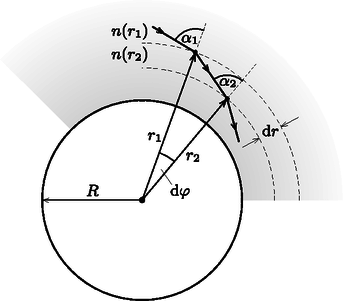 6. ábra 6. ábra
A gömbhéj külső felületén a törésmutató -ről -re változik, így a törési szög a Snellius-Descartes‐törvénnyel számolható: A szög kifejezhető azzal az beesési szöggel is, amely alatt a fénysugár az sugarú gömbhélyhoz ér: ahol a sugár 6. ábrán látható kis szögelfordulása. A fenti két egyenlet, valamint a két szög összegének szinuszára vonatkozó azonosság felhasználásával a következőt kapjuk: | |
Az ábráról leolvasható még az geometriai összefüggés. Ennek segítségével megkapjuk a ,,gömbi Snellius-Descartes‐törvényt'': | |
Megjegyzés: Ez az egyenlet abból a tényből is levezethető, hogy közeghatáron a fény hullámszámvektorának felülettel párhuzamos komponense nem változik meg, így a fény (bolygó középpontjára vonatkoztatott) ,,impulzusnyomatéka'' állandó.
A feladatban , azaz a fény beesési szöge állandó marad a közeghatárokon. Ez azt jelenti, hogy a fénysugár pályájának érintője állandó, szöget zár be a sugárral; a fény trajektóriája tehát logaritmikus spirál.
A fény terjedési sebessége a bolygó középpontjától távolságra: így a sebesség radiális komponense . A felszín eléréséhez szükséges időt tehát a következő integrál adja meg: | |
Az integrálást elvégezve végül a következő eredményt kapjuk: | |
ahol az utolsó lépésben feltételeztük, hogy .
Írjuk fel a szög változási ütemét: amely állandó. A feladat szövege szerint a rádiuszvektor szöggel fordul el a felszín eléréséig (itt egész szám), a felszín eléréséig szükséges időt korábban meghatároztuk, így: A -re kapott korábbi eredményt felhasználva kifejezhető:
Megjegyzés. Természetesen akkor is az indítási pont alatt éri el a lézersugár a bolygó felszínét, ha sugárirányban indítjuk (). Formálisan megkapjuk ezt a megoldást is az helyettesítéssel.
Sarkadi Tamás, Szász Krisztián, Tasnádi Tamás,
Vankó Péter és Vigh Máté |
A feladatok szövege a KöMaL múlt havi számában olvasható. |
 PDF | MathML
PDF | MathML 




