Cím: IMO felkészülés a koronavírus árnyékában, 2020
Szerző(k):  Dobos Sándor 
Füzet: 2020/szeptember, 322 - 325. oldal  PDF  |  MathML 
Témakör(ök): Egyéb írások, Matematika, Nemzetközi Matematikai Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az idei Nemzetközi Matematikai Diákolimpia (IMO) tervezett helyszíne Szentpétervár volt. Ez a beszámoló ennek a különleges évnek a felkészülési krónikája. Először a szakkörök és válogatók történetét mutatjuk be, majd a nyáron sorra került CMC versenyt.
Még március első napjaiban sem lehetett tudni, mi vár ránk. A Rényi Intézet nagytermében március 10-én, kedden a szokásos módon lezajlott a Surányi János emlékverseny, amely a második olimpiai válogatóverseny. A versenyen 44 diák adott be dolgozatot. Ugyanezen a héten, március 13-án, pénteken volt az utolsó központi olimpiai szakkör Budapesten. A viharos gyorsasággal változó járványhelyzet miatt erre  már kevesen jöttek el. Ezen a hétvégén indult az országos veszélyhelyzet és a digitális oktatás. A szakköröket át kellett alakítani, március 27-én az előre meghirdetett olimpiai szakkör időpontjában volt az első zoom-os online olimpiai szakkör. Erre emailben meghívást kapott minden, a Surányi versenyen részt vett diák. A válogatóverseny feladatait beszéltük meg, minden feladat megoldását a javítója mutatta be, kitérve különböző megoldásokra. Szó esett arról is, mire lehetett részpontszámokat kapni. A feladatok felelősei sorban: Dobos Sándor, Kovács Benedek és Borbényi Márton. A megoldások ismeretében lehetett a dolgozatokkal, azok javításával kapcsolatban kérdéseket feltenni, észrevételeket tenni. Amint ezek tisztázódtak, Benedek tájékoztató honlapján1 megjelentette az eredményeket, majd a visszalépések után kialakult az utolsó, kétnapos válogató névsora. Ezt az utóbbi években a Mategye Alapítvány segítségével ‐ melyet ez úton is köszönünk ‐ Kecskeméten rendeztük. A karantén miatt az április végi kecskeméti verseny elmaradt. Helyette együtt izgultunk a lányokért, akik az online EGMO-n remekül szerepeltek.
Az év végére még három online zoom-os olimpiai szakkör maradt (április 24., május 8. és május 22.). Ezeken korábbi évek válogatóversenyeit dolgoztuk fel. A megoldások ismertetésében közreműködött Lenger Dániel, Williams Kada, Baran Zsuzsa. A zoom-os szakkörökön rendszeresen részt vett Kós Géza, aki tanulságos megjegyzésekkel, útmutatásokkal, tanácsokkal segítette a diákokat. Az egyik feladat megoldása kapcsán bemutatta a számelméletben fontos LTE lemmát, és annak alkalmazásához külön gyakorló feladatsort küldött. Minden közreműködőnek nagy köszönet jár! Az online munkaforma lehetőséget teremtett arra is, hogy a csapat korábbi vezetője, Pelikán József és utóda, Frenkel Péter is otthonából ,,jelen lehessen'' a szakkörön.
Aki még nem járt olimpiai szakkörön, annak nehéz elmagyarázni, miért van ennek a szakkörnek különleges hangulata, varázsa. Ahogy belép az ember a terembe, együtt látja az ország különböző részeiről összegyűlve mindazokat, akik az adott évjáratokon a matematikával komolyabban foglalkoznak. Például az idei évben a szakkör törzshelye volt a Szegedről, Győrből, Debrecenből, Kecskemétről és persze Budapest különböző iskoláiból jövő diákoknak. Az online szakkörökön ugyanezek a diákok hosszas utazás nélkül részt vehettek, otthonukból kapcsolódhattak a munkába. Ennek kétségtelenül vannak előnyei is, de mégis hiányzott a személyes találkozás.
A korlátozások enyhítése után június 4-5 ‐én rendeztük meg az utolsó versenyt, ennek javításában a csapatok vezetői mellett segített Borbényi Márton, Csahók Tímea, Imolay András, Kovács Benedek, Lenger Dániel. A versenyen szerzett pontok az említett honlapon követhetők, a kialakult csapatok:
IMO: Beke Csongor, Gyimesi Péter (mindketten a Békásmegyeri Veres Péter Gimnáziumból), Kocsis Anett, Nagy Nándor, Tóth Balázs (ők hárman a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnáziumból), Weisz Máté a Szegedi Radnóti Miklós Kísérleti Gimnáziumból;
MEMO: Fleiner Zsigmond, Füredi Erik, Hámori Janka, Kovács Tamás, Várkonyi Zsombor, Szabó Kornél (Hámori Janka a Szegedi Radnóti Miklós Kísérleti Gimnáziumból, a többiek a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnáziumból).
Idén a MEMO és az IMO is online verseny lesz, a csapatoknak sok sikert kívánunk!
Az utóbbi években Dombóváron volt júniusban olimpiai edzőtábor, ezt idén le kellett mondani. Az IMO sorsa is lassan kezdett körvonalazódni, szeptemberre került át. Júniusban keresték meg a szervezők Frenkel Péter csapatvezetőt azzal, hogy az IMO szokásos idejében egy online világversenyt szerveznek, melynek neve Cyberspace Mathematical Competition, azaz CMC. Az országokat legfeljebb hatfős csapat képviselheti legalább egy lány taggal, vagy legfeljebb nyolcfős csapat legalább két lány taggal. Az IMO csapatból négyen tudták magukat szabaddá tenni a verseny idejére, hozzájuk csatlakozott a MEMO csapat azon négy tagja, akik a válogatókon a legtöbb pontot gyűjtötték. Az utóbbi évek komoly EGMO-s felkészítésének is köszönhető, hogy Anett és Janka révén nyolcfős csapatunk lehetett. A Bolyai Társulat segített a szervezésben. A dombóvári Európa Hotelben írhattuk a versenyt, a nyári melegben is kellemes alagsori konferenciatermekben. A feladatokat csatolva találjuk. A versenyt az MAA (Mathematical Association of America) szervezte az AoPS internetes oldal támogatásával.
Felvetődik a kérdés: hogyan lehet a javítást egységesen végezni? Nos, minden dolgozatot szkennelve elküldtünk; ezeket egy honlapon keresztül minden regisztrált javító megnézhette. Éltem is ezzel a lehetőséggel, és több ország diákjainak dolgozatába belenéztem. A kiküldött pontozási útmutató alapján a csapatvezetők javasoltak egy pontszámot, majd ezt a koordinátorok vagy jóváhagyták, vagy megindult egy egyeztetés. Nálunk a legtöbb javasolt pontszámot azonnal jóváhagyták, néhány esetben kértek segítséget a fordításhoz, egy-két esetben a pontozást kellett finomítani. Minden diák dolgozatainál feladatonként nyomon lehetett követni, hogyan is zajlott az értékelő levélváltás. Ebből kiderült, a koordinátorok komoly munkát végeztek. Kós Géza is közreműködött a versenyen, dolgozott a problémakiválasztó bizottságban. A verseny második feladata az ő javaslata volt, ennek koordinátori csapatában is dolgozott. A versenyről készült tájékoztató kiadványban2 megtalálható az összes szervező és közreműködő.
Az IMO-tól egy kicsit eltért ez a verseny, hiszen mindkét napon 5 órán át lehetett dolgozni és mindkét napon 4 feladatot tűztek ki. A szervezők szándéka szerint ezek egyre nehezedtek, az első könnyebb, a többi IMO szintű volt. Végül 75 ország 555 versenyzője mérte össze tudását. A magyar csapat az országok sorrendjében 14. lett. Kocsis Anett és Weisz Máté arany-, Gyimesi Péter, Hámori Janka és Tóth Balázs ezüst-, Fleiner Zsigmond és Várkonyi Zsombor bronzérmet szereztek, Kovács Tamás dicséretet kapott. A háromnapos dombóvári program a feladatok javításával és a megoldások megbeszélésével zárult. Egy ilyen verseny nyilvánvalóan közel sem teremti meg a szokásos IMO atmoszféráját, másrészről viszont örülhetünk, hogy a járványhelyzet ellenére nemzetközi megmérettetésben vehettünk részt, jó, biztonságos körülmények között, minimális utazással, szervezéssel. A verseny honlapján3 megnézhetjük a videós ,,záróünnepséget'' és a részletes eredménylistát is.
Vajon mit hoz a jövő? Az utazós világversenyek helyett ilyenekre számítsunk? Egyelőre ezt még nem lehet tudni, mindenesetre most készülhetünk és várhatjuk augusztus végén a MEMO-t es a szeptemberi online IMO-t.

 

Írta Dobos Sándor Mátrafüreden, a MaMuT táborban, augusztus 5-én

 
A CMC verseny feladatai
 


 
Első nap
 

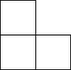
1. feladat. Tekintsünk egy n×n egységnégyzetből álló táblát. A tábla főátlója abból az n egységnégyzetből áll, amelyek a bal felső sarkot a jobb alsóval összekötő átló mentén vannak. Van korlátlan számú ilyen csempénk:
 
 

A csempéket elforgathatjuk. Úgy szeretnénk csempéket elhelyezni a táblán, hogy mind- egyik csempe pontosan három egységnégyzetet fedjen le, a csempék ne fedjék át egymást, a főátló egységnégyzetei közül semelyik se legyen lefedve, és minden más egységnégyzet pontosan egyszer legyen lefedve. Mely n≥2 számokra lehetséges ez?
 
2. feladat. Legyen f(x)=3x2+1. Bizonyítandó, hogy bármely adott pozitív egész n esetén az 
f(1)⋅f(2)⋅...⋅f(n)
szorzatnak legfeljebb n különböző prímosztója van.
 
3. feladat. Legyen ABC olyan háromszög, amelyre AB>BC, és legyen D a BC szakasznak egy változó belső pontja. Legyen E az a pont az ABC háromszög körülírt körén, a BC-nek A-val ellentétes oldalán, amelyre BAE∢=DAC∢. Legyen I az ABD háromszög beírt körének középpontja, és legyen J az ACE háromszög beírt körének középpontja. Bizonyítandó, hogy az IJ egyenes átmegy egy rögzített ponton, amely független D-től.
 
4. feladat. Legyen n páratlan pozitív egész. Egy n×n mezőből álló sakktábla bizonyos mezőit zöldre színezzük. Az derül ki, hogy a sakkjáték-beli király bármely zöld mezőről bármely másik zöld mezőre el tud jutni lépések véges sorozatával úgy, hogy eközben csak zöld mezőkön halad át. Bizonyítandó, hogy ezt legfeljebb n2-12 lépésben mindig meg tudja tenni. (A király egy lépésben egy mezőről akkor és csak akkor léphet át egy másikra, ha a két mezőnek van közös csúcsa vagy oldala.)
 
Második nap
 

5. feladat. Egy táblára 2020 darab pozitív egész szám van felírva. Zuming minden percben letöröl két számot és helyettük az összegüket, különbségüket, szorzatukat vagy hányadosukat írja fel. Ha például Zuming a 6 és 3 számokat törli le, akkor a {6+3,6-3,3-6,6⋅3,6:3,3:6}={9,3,-3,18,2,12} halmaz egy elemével helyettesíti őket. 2019 perc után Zuming a -2020 számot írja fel egyetlenként a táblára. Mutassuk meg, hogy ugyanezen szabályokkal, ugyanabból a 2020 darab egész számból indulva az is lehetséges lett volna, hogy Zuming egyetlen számként a 2020-szal fejezze be az eljárást.
 
6. feladat. Határozzuk meg mindazon n≥3 egészeket, amelyekre a következő állítás igaz: Ha a P konvex n-szögnek n-1 oldala egyenlő hosszúságú és n-1 szöge egyenlő nagyságú, akkor P szabályos sokszög. (Egy sokszög szabályos, ha minden oldala egyenlő hosszúságú és minden szöge egyenlő nagyságú.)
 
7. feladat. Egy n×n méretű tábla n2 mezejének mindegyikét feketére vagy fehérre színezzük. Jelölje ai a fehér mezők számát az i-edik sorban, és jelölje bi a fekete mezők számát az i-edik oszlopban.
 
Határozzuk meg ∑i=1naibi maximális értékét a tábla összes kiszínezésére nézve.
 
8. feladat. Legyen a1,a2,... pozitív valós számok végtelen sorozata úgy, hogy minden pozitív egész n esetén
a1+a2+...+ann=a12+a22+...+an12n+1.
Bizonyítandó, hogy az a1,a2,... sorozat konstans.
1http://benoke98.f.fazekas.hu/olimpia/

2https://data.artofproblemsolving.com/images/contests/CMC_brochure.pdf

3https://artofproblemsolving.com/contests/cmc