Kezdőlap


Cím:	Olimpiai előkészítő feladatok (3.)
Füzet:	1977/december, 219 - 220. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ebben a rovatban havonként tíz‐tíz olyan érdekes ‐ könnyebb vagy nehezebb ‐ feladatot mondunk el, amelyek előkészítőül szolgálnak a Matematikai Diákolimpiára. A feladatok megoldásait nem kérjük beküldeni, a megoldásokat sem fogjuk ismertetni. Az érdeklődők a feladatokkal kapcsolatos kérdéseikkel forduljanak a szerkesztőséghez. Leveleikre írásban válaszolunk.
1. Adott a síkban 6 pont: $P_{1}, P_{2}, P_{3}, Q_{1}, Q_{2}, Q_{3}$ úgy, hogy a $\vec{P_{i} P_{k}}$ párhuzamos és egyirányú a $\vec{Q_{k} Q_{i}}$ -ral ( $i = 1, 2, 3$ ). Bizonyítsuk be, hogy ekkor a $P_{1} Q_{1}$ , $P_{2} Q_{2}$ , $P_{3} Q_{3}$ egyeneseknek van közös pontja.

2. Az

A B C

háromszög mindegyik oldala fölé, kefelé szerkesszünk négyzetet, majd a háromszög csúcsainál adódó két-két szakaszt egészítsük ki paralelogrammává. A paralelogrammák új csúcsai legyenek rendre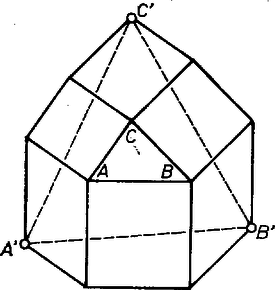

A', B'

és

C'

Igazoljuk, hogy

a)

A B C

háromszög és az

A' B' C'

háromszögek súlypontja egybeesik;

b)

A' B' C'

oldalai áthaladnak egy-egy négyzet középpontján;

c)

A A'

merőleges a

B C

oldalra.

3. Legyen

A B C

szabályos háromszög, továbbá legyenek

A A_{1} A_{2}, B B_{1} B_{2}, C C_{1} C_{2}

egyező körüljárású szabályos háromszögek. Az

A_{2} B_{1}, B_{2} C_{1}, C_{2} A_{1}

szakaszok felezőpontjai

X, Y, Z

. Mutassuk meg, hogy

X Y Z

is szabályos háromszög.

4. Legyenek

A, B, C, D

és

E

egy sík pontjai. Jelöljük

T_{X Y Z}

-vel az

X Y Z

háromszög előjeles területét (azaz ha

X

Y

Z

ebben a sorrendben pozitív körüljárású, a háromszög területe pozitív, az ellenkező esetben negatív.) Bizonyítsuk be, hogy

\begin{matrix} T_{E A B} \cdot T_{B C D} + T_{E A D} \cdot T_{E B C} = T_{E A C} \cdot T_{E B D} . \end{matrix}

5. Az

a,  b,  c,  d

egy síkben levő vektorok összege

0

. Mutassuk meg, hogy

\begin{matrix} | a | + | b | + | c | + | d | \geq | a+d | + | b+d | + | c+d | . \end{matrix}

6. Adott a síkben

n

egységvektor úgy, hogy összegük

0

. Bizonyítsuk be, hogy minden

1 \leq k \leq n

-re kiválasztható közülük

k

darab úgy, hogy ezek eredőjének hossza legfeljebb 3.

7. Adott néhány vektor a síkban, melyek hosszainak összege pontosan 4. Bizonyítandó, hogy kiválasztható közülük néhány, melyek eredőjének hossza legalább 1.

a .)

Egy tetraéder súlyvonalai egenlő hosszúak. Igazoljuk, hogy ekkor a szemközti élek is egyenlő hosszúak.

b)

Egy tetraéder súlyvonalai merőlegesek a szmeközti lapra. Igazoljuk, hogy a tetraéder szabályos.

a)

Két páros oldalszámú konvex sokszög oldalfelező pontjai egybeesnek. Bizonyítsuk be, hogy területük egyenlő.

b)

Egy konvex

n

-szög területe

T

, az oldalfelező pontok által meghatározott

n

-szög területe

F

. Az oldalakat

p / q

aránybn osztjuk (

p + q = 1

), az osztópontok kal meghatározott

n

-szög területe

S

. Bizonyítsuk be, hogy

\begin{matrix} S = {(p + q)}^{2} T + 4 p q F . \end{matrix}

10. Egy háromszög köré írt kör középpontjából a csúcsokba mutató vektorok

a,  b,  c

, továbbá

λ_{1} a + λ_{2} b + λ_{3} c = 0

. Fejezzük ki a

λ

-k arányát a háromszög szögeivel.

Ajánlott irodalom: Reiman István: Geometriai feladatok megoldása a komplex számsíkon; Reiman István: Vektorok a geometriában; (Középisk. Szakköri Füzet, Tankönyvkiadó, 1971 Bp.); Lukács Ottó: Koordináta-geometria vektorokkal a síkban és a térben; Skljarszkij-Csencov-Jaglom: Válogatott feladatok és tételek az elemi geometria köréből, Geometria II. (Planimetria) (Tankönyvkiadó 1972 Bp.)