Kezdőlap


Cím:	OKTOTÓ
Szerző(k):	Tusnády Gábor
Füzet:	1977/november, 106 - 110. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Oktotó

(Rovatvezető: Tusnády Gábor)

Az alábbi feladatokat bárki megoldhatja foglalkozásra és életkorra való tekintet nélkül. Tulajdonképpen nem is kell a feladatokat megoldani a szó hagyományos értelmében, elég megtippelni az eredményt. A tippeket a mellékelt szelvényen, vagy hozzá hasonló táblázatban lehet beküldeni.

Számtotó

1. Melyik az a legkisebb,

3

-mal osztható pozitív egész szám, amelyik

2

-vel,

4

-gyel,

8

-cal,

13

-mal és

19

-cel osztva egyet ad maradékul?
2. Egy

6

egység oldalú, négyzet alakú földdarabon

4

testvér osztozott az ábra szerint. Hány egységnyi földet kapott az, akinek a legtöbb jutott közülük?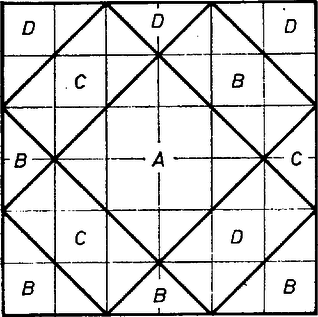

3. Melyik az szám, amelyik négyzetgyökének, negyedik gyökének, nyolcadik gyökének és

13

-adik gyökének az összege

19

?
4. Mennyi az ábrán látható test térfogata, ha csúcsai egy egységsugarú gömbön vannak? (A testet

12

szabályos ötszög és

20

szabályos háromszög határolja.)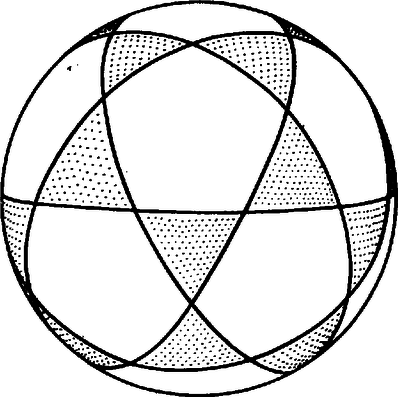

5. Hány százalékuk prímszám az ezernél nem nagyobb pozitív egészeknek?
6. Milyen messze van egy

10

egység sugarú, homogén anyagból készült, félkör alakú lemez súlypontja a kör középpontjától?
7. Feldobunk három kockát, amelyek mindegyike egytől hatig van megszámozva. Igaz-e a következő állítás? "Annak valószínűsége, hogy a dobott számok összege

9

, vagy annál kisebb lesz, legalább annyi, mint annak a valószínűsége, hogy

9

-nél nagyobb lesz." (Ha úgy gondolja, hogy igaz, írjon

9

-et. Ha nem, melyik a legkisebb szám, amelyikre igaz?)
8. Maximálisan hány kapcsolat létesíthető egy hírközlő csatornán a következő feltételek mellett?
a) A csatornán öt különböző hang használható.
b) Minden jel fizikailag azt jelenti, hogy az egyik hang után egy másik, tőle különböző hangot adunk.
c) Minden kapcsolathoz két különböző jel kell, de ezekhez csak három-féle hangot lehet felhasználni.
d) A különböző kapcsolatok jelei különbözőek.

Beküldhető 1977. december 20-ig. Címünk: KÖMAL/OKTOTÓ
1443 Budapest, Postafiók 129.

\begin{matrix} 1977. november SZÁMTOTÓ  Sorszám: 3/1 \\ SZÁM & KÓD & TIPP \\ 1. & Legkisebb szám \\ 2. & Átdarabolás \\ 3. & \sqrt[]{x} + \sqrt[4]{x} + \sqrt[8]{x} + \sqrt[13]{x} = 19 \\ 4. & Dodeka‐ikozaéder térfogata \\ 5. & Ezernél kisebb prímek száma osztva tízzel \\ 6. & Félkör súlypontja \\ 7. & Három dobókocka \\ 8. & Kódolás \\ KVADRATIKUS ELTÉRÉS \end{matrix}

Betűtotó
1. Melyik a legnagyobb az alábbi négy szám közül?
A) Az első száz egész szám reciprokának az összege.
B) Az első száz egész szám mértani közepe.
C)

100 \sqrt[100]{100} - 100

.
D) Az

a_{0} = 5

a_{n + 1} = a_{n} + 1 / a_{n}

feltételekkel meghatározott sorozat második tagja.
2. Melyik testvérnek jutott a számtotó 2. példájában a legtöbb föld?
3. Nevezzük a racionális számok valamely részhalmazát generátornak, ha az nem tartalmazza az összes racionális számot, de bármelyik racionális szám előállítható mint két, ebben a részhalmazban levő szám összege. Melyik igaz az alábbi állítások közül?
A) Nincs generátor.
B) Van generátor, sőt az is igaz, hogy egy generátorból tetszőleges véges sok elemet elhagyva, ismét generátort kapunk.
C) Van olyan generátor, amelynek bármelyik elemét hagyjuk is el, az megszűnik generátor lenni.
D) Sem A), sem B), sem C) nem igaz.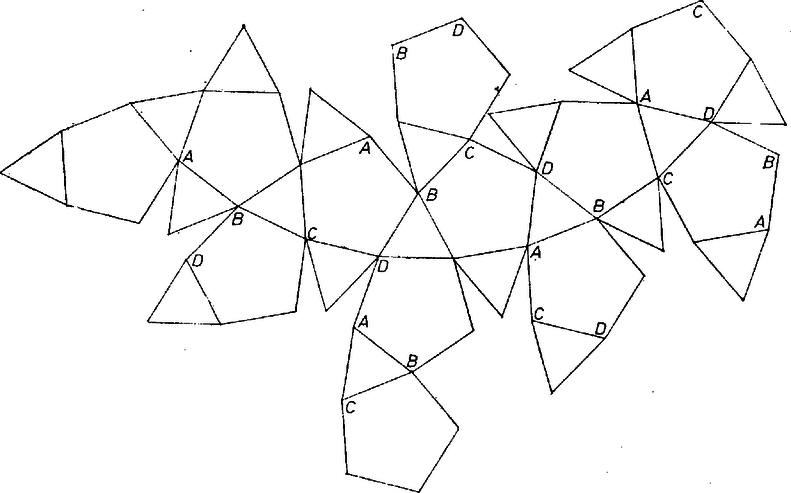

4. Az ábrán látható hálózatból egy konvex test burkolata hajtható össze. A test csúcsai közül többféleképpen is összeszedhető egy oktaéder hat csúcsa. Az ábrán négy oktaédert is megjelöltünk, közülük azonban csak egy jó. Melyik az ?
5. Melyik nem igaz az alábbi állítások közül (

n > 1

)?
A) Bárhogy vesszük ki

n

elem összes permutációi közül ezek felét, ezeket egymás után alkalmazva minden permutációt megkapunk.
B)

n

elem összes permutációi közül ki lehet választani

n (n - 1)

darabot úgy, hogy ezeket egymás után alkalmazva ‐ valamilyen sorrendben ‐ minden permutációt megkapjunk.
C)

n

elem összes permutációi közül

n - 1

darabot is ki lehet választani úgy, hogy rendelkezzenek a B)-beli tulajdonsággal.
D)

n

elem összes permutációi közül kettőt is kiválaszthatunk úgy, hogy a B)-beli tulajdonságuk meglegyen.
6. Vegyük a tetraéder, kocka, oktaéder, dodekaéder és ikozaéder élfelező pontjainak konvex burkát. Melyiké azonos közülük az ikozaéderével?
A) A tetraéderé ; B) a kockáé ; C) az oktaéderé ; D) a dodekaéderé.
7. Melyik megoldatlan az alábbi problémák közül?
A) Igaz-e, hogy ha egy társaságban ugyanannyi fiú van, mint lány, és a fiúk minden részhalmazára igaz, hogy legalább annyian vannak azok a lányok, akik közülük legalább egyet ismernek, mint az illető fiúk, akkor lehet a társaság tagjait párba állítani úgy, hogy minden párba ismerősök kerüljenek? (Az ismeretség kölcsönös.)
B) Jelöljük az

x

-nél kisebb prímek számát

π (x)

-szel. Konvergens-e a

(π (n) lg n) / n

sorozat, és ha igen, ismeretes-e a határértéke?
C) Találhatók-e tetszőleges, a (

0

π

) intervallumban négyzet-integrálható

f (x)

függvényhez olyan

{a_{1}, a_{2}, ...}

{b_{1}, b_{2}, ...}

végtelen sorozatok, hogy az

\begin{matrix} f_{n} (x) = \sum_{j = 1}^{n} (a_{j} cos j x + b_{j} sin j x) \end{matrix}

sorozatnak majdnem minden

0 ≦ x ≦ π

mellett

f (x)

legyen a határértéke? (Egy függvény négyzet-integrálható, ha négyzete integrálható. Egy valós számokra vonatkozó állítás majdnem minden valós számra igaz, ha tetszőleges

ε > 0

-hoz találhatók olyan

{u_{i}, < v_{i}, i = 1, 2, ...}

számok, hogy

\sum_{i = 1}^{\infty} (v_{i} - u_{i}) < ε

, és minden olyan szám, amelyikre az állítás nem igaz, valamelyik

(u_{i}, v_{i})

intervallumban van.)
D) Átdarabolható-e az egységsugarú kör egy

\sqrt[]{π}

oldalú négyzetté? (Azaz felbontható-e a zárt körlemez véges sok diszjunkt halmaz egyesítésévé úgy, hogy azokból alkalmas síkbeli elmozgatások után összerakható legyen a négyzet. A halmazokról semmit nem követelünk meg.)
8. Jelöljük

p (k)

-val az 1977-ben a lottón a

k

-adik játékhéten kihúzott számok között a prímek számát, és legyen

P

p (47)

p (48)

p (49)

p (50)

p (51)

számok minimuma. Melyik lesz igaz az alábbi állítások közül?
A)

P ≦ 1

; B)

P = 2

; C)

P = 3

; D)

P ≧ 4

.

Beküldhető 1977. december 20-ig. Címünk: KÖMAL/OKTOTÓ
1443 Budapest, Postafiók 129.

\begin{matrix} \begin{matrix} A BEKÜLDŐ ADATAI \\ Neve:..... \\ Címe:..... \\ Foglalkozása:..... \\ Iskolája:..... \\ ..... \end{matrix} & \begin{matrix} 1977. november  Sorszám: 3/1 \\ SZÁM & KÓD & TIPP \\ 1. & Melyik a legnagyobb? \\ 2. & Átdarabolás \\ 3. & Generátorok \\ 4. & Oktaéderek \\ 5. & Permutációk \\ 6. & Ikozaéder \\ 7. & Melyik megoldatlan? \\ 8. & Lottó prímei \\ A TALÁLATOK SZÁMA \end{matrix} \end{matrix}

A januári oktotó eredményei

A számtotó nyertese: Baksai Róbert (Győr, Révai M. Gimn.), kvadratikus eltérése

65 \cdot 10^{- 20}

. Jó eredményt értek el a következők: Rosanits György (Budapest,

10^{- 16}

), Molnár Balázs (Budapest,

10^{- 15}

), Seress Ákos (Budapest,

10^{- 15}

), Lévai Pál (Budapest,

10^{- 13}

), Tóth Csaba (Nagylózs,

10 - 4

). A többiek kvadratikus eltérése:

1

4

17

19

;

28

225

331

830

1600

\begin{matrix} SZÁM & SZÁMTOTÓ & BETŰTOTÓ \\ 1. & Legnagyobb gyök & 0,960 948 596 5 & Érme & x \\ 2. & 100 (\sqrt[3]{1977} - \sqrt[3]{1976}) & 0,211 648 017 4 & Totó & 1 \\ 3. & sin y = (π / 2 - cos y) (π / 2 + y) & 0,334 899 402 5 & Kártya & 1 \\ 4. & Dodeka‐ikoza csillag & 28,624 573 523 9 & Kocka & 1 \\ 5. & Összeg maximumak & 3,651 483 716 7 & Lottós & 2 \\ 6. & Tört maximuma & 4 & Lottóösszeg & 2 \\ 7. & Kecskemét adója & 15 & Kockaösszeg & 2 \\ 8. & Arthur király lovagjai & 1,5 & Tiszta fej & 1 \end{matrix}

A betűtotó nyertese: Peták Kálmán (Szolnok), találatainak száma: 8. Ugyancsak nyolc találatot értek el a következők: Baksai Róbert (Győr), Kerényi István (Budapest), Lévai Pál (Budapest), Molnár Balázs (Budapest) és Seress Ákos (Budapest). Hét találatot hatan, hatot öten, ötöt egy, négyet ketten értek el.
Baksai Róbert és Peták Katalin 100-100 Ft-os könyvutalványt nyertek. Nyereményüket postán küldjük el.