Cím: Az Iskolarádió matematika szakköre
Füzet: 1977/április, 169 - 174. oldal  PDF  |  MathML 

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

AZ ISKOLARÁDIÓ MATEMATIKA SZAKKÖRE

 

A legközelebbi adásunk 1977. május 23án (hétfőn) a 3. műsorban hangzik el 15.30‐16.00 óráig. Címe: A nagy számok törvénye és következményei.
Ezzel az adással egy négy részes sorozat zárul. Az előző adások címe (és időpontja, valamint KÖMAL-beli helye) a következő volt: Válasszuk a valószínűbbet (II. 28.‐54. kötet 1. szám, 26‐29. old.), Fogadjunk (III. 28.‐54. kötet 2. szám, 75‐77. old.). Mikor igazságos egy játék? (IV. 25.‐54. kötet 3. szám, 121‐124. old.)
 


Markov és Csebisev egyenlőtlensége

 

A számok tetszőleges összességét számcsoportnak neveztük. A ξ számcsoport várható értékét E(ξ)-vel, szórását D(ξ)-vel jelöltük, G(ξ∈H) jelölte ξH-hoz tartozó elemeinek a számát, G(ξ) pedig ξ összes elemének a számát.
Tétel. Legyen ξ tetszőleges számcsoport, csak annyit tegyünk fel, hogy ξ elemei nem negatívak, és legyen A tetszőleges pozitív szám, akkor
G(ξ≧A)≦1AG(ξ)E(ξ).

Bizonyítás. Jelöljük η-val azt a számcsoportot, amelyet ξ-ből úgy kapunk, hogy elhagyjuk az elemek közül az A-nál kisebbeket, és jelöljük e két számcsoport elemeinek az összegét S(ξ)-vel, S(η)-val. Mivel feltevésünk szerint ξ elemei nem negatívak, nem negatív a ξ-ből η-ba át nem került számok összege is, tehát
S(ξ)≦S(η).
Ez utóbbi viszont legalább AG(η), hiszen η-ban nincs A-nál kisebb elem. Mivel G(η)=G(ξ≥A), ez azt jelenti, hogy
S(ξ)≧AG(ξ≧A).
Ebből viszont E(ξ)=S(ξ)/G(ξ) miatt már következik a bizonyítandó, Markovtól származó egyenlőtlenség.
 

Tétel. Legyen ξ tetszőleges számcsoport, és legyen ε tetszőleges pozitív szám, akkor
G(|ξ-E(ξ)|≧ε)≦1ε2G(ξ)D2(ξ).

Bizonyítás. Alkalmazzuk Markov egyenlőtlenségét az
η=(ξ-E(ξ))2
számcsoportra. Ennek az elemeit úgy kapjuk meg ξ elemeiből, hogy mindegyikből levonunk E(ξ)-t, és a különbségeket rendre négyzetre emeljük. Az η számcsoportnak nyilván ugyanannyi eleme van, mint ξ-nek, és η várható értéke nem más, mint ξ szórásnégyzete:
G(η)=G(ξ),E(η)=D2(ξ).
Így Markov egyenlőtlenségéből következik, hogy
G(|ξ-E(ξ)|≧ε)=G(η≧ε2)≧1ε2G(η)E(η)=1ε2G(ξ)D2(ξ),
ami épp a bizonyítandó, Csebisevtől származó egyenlőtlenség.
 

A nagy számok törvénye és következményei
 

Tétel. Legyenek a ξ1, ξ2, ..., ξn, ... számcsoportok azonosak, és legyen ε tetszőleges pozitív szám, akkor van olyan N, hogy minden n>N mellett
G(|1n∑i=1nξi-E(ξ1)|≧ε)<εG(1n∑i=1nξi).

Bizonyítás. Jelöljük az 1n∑i=1nξi számcsoportot ηn-nel. Ezt tehát úgy kapjuk meg, hogy összeadjuk a ξ1, ξ2, ..., ξn számcsoportokat, és a kapott számcsoport minden elemét elosztjuk n-nel. Előző adásunkban beláttuk, hogy számcsoportok összegének várható értéke és szórásnégyzete a tagok várható értékének, illetve szórásnégyzetének összege. Emiatt
E(ξ1+ξ2+...+ξn=nE(ξ1),D2(ξ1+ξ2+...+ξn)=nD2(ξ1).


Ha egy számcsoport elemeit elosztjuk n-nel, az új számcsoport várható értéke is, szórása is az eredeti n-ed része lesz, tehát
E(ηn)=E(ξ1),D2(ηn)=1nD2(ξ1).
Így Csebisev egyenlőtlensége szerint
G(|ηn-E(ξ1)|≧ε)≦1ε2G(ηn)D2(ηn),
ez pedig kisebb lesz εG(ηn)-nél, ha
n>1ε3D2(ξ1),
tehát N=1ε3D2(ξ1) mellett teljesül a tételben szereplő egyenlőtlenség.
Ha például a ξ1={0,1,2,3,4,5} számcsoportból indulunk ki, az
sn=ξ1+ξ2+...+ξn
számcsoport elemeit (ahol ξi azonos ξ1-gyel) úgy is megkaphatjuk, hogy meghatározzuk a
pn(x)=(1+x+x2+x3+x4+x5)n
polinom együtthatóit. Könnyen látható ugyanis, hagy sn-ben a j szám pontosan annyiszor fordul elő, mint amennyi pn-ben xj együtthatója. A mellékelt 1. táblázatban megadjuk néhány n és j mellett a megfelelő együtthatókat. Hatványozás közben azt tapasztaljuk, hogy adott n esetén a nagyobb együtthatók egy bizonyos x hatvány körül helyezkednek el, és ez a ,,sűrűsödési hely'' egyenletes sebességgel halad előre ahogy n nő. Így van ez, akármilyen más,
p1(x)=∑i=0kaixi,
egészegyütthatós polinomból indulunk is ki, és a sűrűsödési hely vándorlási sebessége csak annak a ξ1 számcsoportnak a várható értékétől függ, amelyben az i szám ai-szer fordul elő, hiszen tételünk szerint az n-edik hatvány sűrűsödési helye éppen nE(ξ1).
Joggal vetődik fel ezek után a kérdés, mi köze mindennek a véletlen számokhoz? Hát az, hogy ha egy kocka lapjaira a 0, 1, 2, 3, 4, 5 számokat írjuk, és a kockát sokszor feldobjuk, akkor a dobott számok átlaga egyre közelebb lesz ξ={0,1,2,3,4,5} számcsoport várható értékéhez, 2,5-hez. Vagy ha n dobásban megszámoljuk a dobott számok között mondjuk a párosak számát, és a kapott számot elosztjuk n-nel, a hányados (a páros számok ,,relatív gyakorisága'') tart a G(ξ páros)/G(ξ) hányadoshoz. Szokás ennek alapján tetszőleges ξ számcsoport és a valós számok tetszőleges H részhalmaza mellett a G(ξ∈H)/(G(ξ)) hányadost a ξ∈H esemény valószínűségének nevezni, és ezt a hányadost P(ξ∈H)-val jelölni:
P(ξ∈H)=G(ξ∈H)G(ξ).
Könnyen látható, hogy tételünk azt jelenti, hogy a ξ számcsoport által generált véletlen szám elég hosszú ξn realizációjában a G(ξn∈H)/G(ξn) relatív gyakoriság közel lesz a P(ξ∈H) valószínűséghez.
Örülnénk azonban, ha az érzékeny fülű olvasó hitetlenkedve fogadná mindezt. Hiszen tételünk csak számcsoportokról szól, és nem véletlen számokról. Mi tudjuk, hogyan kell véletlen számokat összeadni. Kérdés, hogy a véletlen számok tudják-e ezt. Nem tudjuk, hogy a számcsoportok általunk adott definíciója megfelel-e a véletlen számok összegezési szabályának. Igen is, meg nem is.
Igyekeztünk a definíciónkat úgy kialakítani, hogy közben állandóan a véletlen számokra gondoltunk. Egy dologról azonban nem szabad megfeledkeznünk: mi hallgatólagosan mindig feltettük, hogy a véletlen számot valamilyen szerkezet, berendezés, eljárás állítja elő, ez az apparátus akárhány számot elő tud állítani, és az egyes számok nem befolyásolják egymást. A valószínűségszámításban ezt úgy mondják, hogy az egyes számok függetlenek és egyforma eloszlásúak. Végül is azt kaptuk tehát, hogy annak, hogy a tételünk véletlen számokra is igaz legyen, épp az a feltétele, hogy a véletlen számok úgy viselkedjenek, mint a számcsoportok.
 

A centrális határeloszlástétel

 

Tétel. Legyenek a ξ1, ξ2, ..., ξn, ... számcsoportok azonosak, és jelöljük az
ηn=∑i=1nξi-nE(ξ1)nD(ξ1)
számcsoport eloszlásfüggvényét Fn(x)-szel. Akkor az {Fn(x),n=1,2,...} sorozat tetszőleges x mellett konvergál, és a határértéke az eredeti ξ1 számcsoport eloszlásától független Φ(x) szám.
Ez a tétel Gausstól származik, a Φ(x) eloszlásfüggvényt Gauss vagy normális eloszlásnak nevezik.
Tulajdonképpen nem volna lehetetlen ezt a tételt ismereteink alapján bebizonyítani, erre itt lényegében csak hely (és idő) hiány miatt nem kerül sor. A ξ1=0,1,2,3,4,5 számcsoport mellett az F14(x) függvény néhány értékét a megfelelő Φ(x) számokkal a mellékelt 1. táblázatban mutatjuk be. Javasoljuk az olvasónak, hogy tetszőlegesen választott ξ1 számcsoportból kiindulva állítsa elő az Fn(x) eloszlásfüggvényeket, tapasztalni fogja tételünk helyességét. Mi a mellékelt ábrán a ξ1={0,1,2} számcsoport esetében a szemléletesség kedvéért magának a (ξ1+ξ2+...+ξn) összegnek mutatjuk be az eloszlásfüggvényét néhány n-r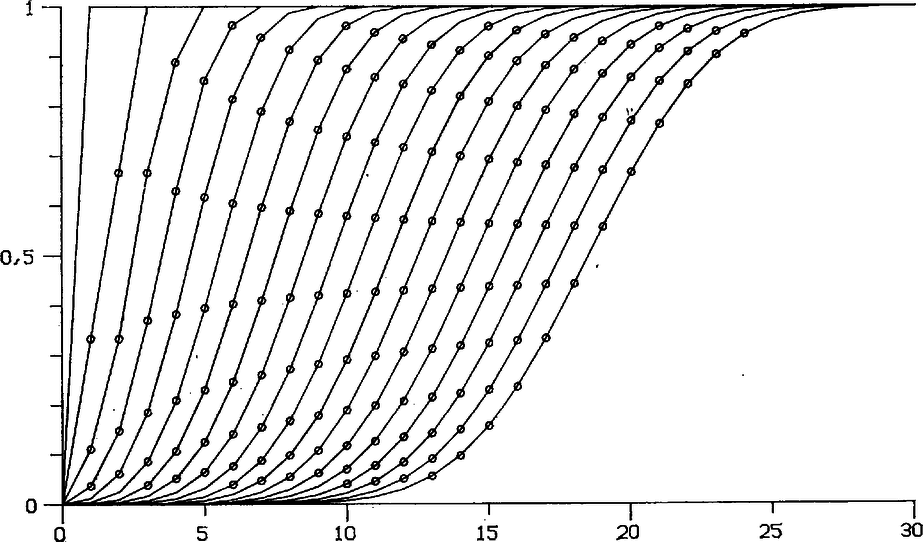e.
 


 


A kitűzött feladatok megoldása

 

1. feladat. A mesterségesen előidézett intelligencia romlásának a sebessége egyenes arányban van a növekedés mennyiségével.
2. feladat. A nyolctalálatos szelvény: x, 1, 1, 1, 2, 2, 2, 1. (A mellékelt 2. táblázatban megadjuk a szóban forgó változók néhány értékének a valószínűségét.)
3. feladat. A regresszió egyenes egyenlete: y=0,5x+80,5. (Általában y=b(x-x¯)+y¯ ahol b=∑i=1n(yi-y¯)(xi-x¯)/∑i=1n(xi-x¯)2).
4. feladat. A mellékelt 3. táblázatban megadjuk a szóban forgó változók eloszlásfüggvényét.
5‐6. feladat. Megoldásukat később közöljük.
 

 1. táblázat
(1+x+x2+x3+x4+x5) hatványai és a normális eloszlás


j123 4714xjF14(xj)Φ(xj)0111111  11234714  21361028105  314102084560  41515352102 380  51621564628 568  65258091727 118  74271041 66777 324  83271252 807202 020  92251404 417489 580  101211466 5381 110 746  11151409 1422 376 192-3,6770,00010,0001  121012512 1174 820 543-3,5210,00010,0002  13610415 2679 316 594-3,3650,00020,0004  1438018 32717 218 995-3,2080,00050,0007  1515620 99330 529 240-3,0510,00080,0011  163522 96752 063 571-2,8950,00150,0019  172024 01785 593 522-2,7380,00260,0031  181024 017135 917 523-2,5820,00430,0049  19422 967208 814 424-2,4260,00700,0076  20120 993310 829 610-2,2690,01100,0116  2118 327448 854 900-2,1130,01670,0173  2215 267629 486 676-1,9560,02470,0253  2312 117858 182 052-1,8000,03570,0359  249 1421 138 276 503-1,6430,05020,0502  256 5381 469 971 230-1,4870,06900,0685  264 4171 849 435 329-1,3300,09260,0918  272 8072 268 186 480-1,1740,12150,1201  281 6672 712 905 781-1,0170,15610,1546  299173 165 803 382-0,8610,19650,1947  304263 605 583 723-0,7040,24250,2408  312104 008 970 980-0,5480,29370,2919  32844 352 660 949-0,3910,34920,3479  33284 615 482 690-0,2350,40810,4071  3474 780 499 451-0,0780,46910,4689  3514 836 766 584-0,0780,53090,5311

 

 2. táblázat
A januári betűtotó változóinak az eloszlása (a lottóösszeg lehetséges értékeit 10-zel osztottuk, a megfelelő valószínűségeket 10-zel szoroztuk)


SzámÉrmeTotóKártyaKockaLottóLottó-Kocka-Tisztaősszegősszegfej00,0000,0030,0130,194---0,000  10,0000,0240,0800,3490,056--0,010  20,0000,0780,2060,2790,0530,000-0,203  30,0010,1560,2860,1300,0510,000-0,309  40,0050,2140,2390,0390,0480,000-0,228  50,0150,2140,1250,0080,0460,0000,0000,128  60,0370,1600,0420,0010,0440,0010,0010,064  70,0740,0920,0090,0000,0420,0010,0020,031  80,1200,0400,0010,0000,0400,0020,0050,015  90,1600,0130,0000,0000,0380,0040,0090,007  100,1760,0030,000-0,0360,0060,0160,003  110,1600,0010,000-0,0340,0090,0260,001  120,1200,0000,000-0,0320,0120,0390,001  130,0740,0000,000-0,0310,0170,0540,000  140,0370,000--0,0290,0230,0690,000  150,015---0,0280,0290,0840,000  160,005---0,0260,0360,0950,000  170,001---0,0250,0430,1000,000  180,000---0,0230,0500,1000,000  190,000---0,0220,0560,0950,000  200,000---0,0210,0610,0840,000  21----0,0200,0650,069-  22----0,0190,0680,054-  23----0,0170,0680,039-

 

 3. táblázat
Kilenc kockán dobott piros lapok számának az eloszlása, ha egy kockán k piros lap van


Legfeljebbk=0k=1k=2k=3k=4k=5k=601,0000,1940,0260,0020,0000,0000,000  11,0000,5430,1430,0200,0010,0000,000  21,0000,8220,3770,0900,0080,0000,000  31,0000,9520,6500,2540,0420,0010,000  41,0000,9910,8550,5000,1450,0090,000  51,0000,9990,9580,7460,3500,0480,000  61,0001,0000,9920,9100,6230,1780,000  71,0001,0000,9990,9800,8570,4570,000  81,0001,0001,0000,9980,9740,8060,000  91,0001,0001,0001,0001,0001,0001,000

 


Sorozatunk készítői

Sorozatunk négy iskolában készült a következő tanulók és tanárok részvételével.
Berzsenyi D. Gimnázium. Tanulók: Cseh Tibor, Horváth Zoltán, Iring Zoltán, Karsai Ferenc, Klebercz Attila, Kormos Mária, Korom Melinda, Kővári Klára, Radácsy Katalin, Szathmári György. Tanárok: Simon Judit és Nemetz Tibor
Dózsa Gy. Gimnázium. Tanulók: Bodrog Beáta, Bubcsó Gábor, Galambos Sándor, Gróf Jolán, Karikás Ágnes, Kövesdi Kinga, Zeibig Károly. Tanárok: Tusnády Gáborné és Tusnády Gábor.
Móricz Zs. Gimnázium. Tanulók: Bach Judit, Bacsó Piroska, Bajnok Béla, Butyka Beáta, Fazekas Eszter, Győrbiró Bea, Karády Zoltán, Kiss Péter, Klimó Gábor, Kovács István, Molnár Géza, Papp László, Péter Katalin, Solt Gábor, Schindele Miklós, Szentiványi Árpád, Tóth Zoltán, Varga László, Venczel György, Zimonyi Ferenc, Zsáry Anikó. Tanár: Némethy Katalin.
Radnóti M. Gimnázium. Tanulók: Ábrahám Erzsébet, Balázs Péter, Balogh Ágnes, Farkas Miklós, Galánfi Klára, Gál Róbert, Ganczer Sándor, Greschik Gyula, Hankó Zsuzsa, Héder Barna, Kapus András, Koncz Károly, Konrád Zoltán, Prazsák Gabriella, Papp János, Ungár Katalin, Váli Ruth, Varga Zsolt, Zimányi Krisztina. Tanárok: Gábos Adél, Bognár Jánosné.