Cím:	Számítástechnikai rovat (6.)
Füzet:	1977/április, 163 - 168. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 6.   A legutóbb kitűzött feladatok és azok megoldása:   1. feladat. Készítsünk FUNCTION szubrutint, amely tetszőlegesen megadott koordinátájú két pont közötti távolság értékét számítja ki.   Megoldás. Mivel a távolságot a $\sqrt[]{{\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2}$ képlettel számítjuk, tulajdonképpen utasításfüggvénnyel is megoldható lenne a feladat. FUNCTION szubrutinnal a programrész az alábbi:   ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{FUNCTION TAAV X1,X2,Y1,Y2}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{TAAV=SQRT<math xmlns="http://www.w3.org/1998/Math/MathML"></math>((X1‐X2)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo><mo>*</mo></math>2+(Y1‐Y2)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo><mo>*</mo></math>2<math xmlns="http://www.w3.org/1998/Math/MathML"></math>)}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{RETURN}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{END}}\hfill \end{array}}$   2. feladat. Készítsünk még egy FUNCTION szubrutint, amely legfeljebb 30 számadat átlagát számítja ki (az adatokat egy 30 elemű tömb, az adatok számát egy egész típusú azonosító tartalmazza). Megoldás. Az átadásra kerülő adatokat egy tömbazonosító tartalmazza, ezért ez a feladat utasításfüggvénnyel már nem oldható meg. Az adatok pontos számát előre nem tudjuk, emiatt azt az N számot is meg kell adnunk, amely a tömbben levő átlagolandó adatok számosságát jelenti. A feladat értelmében természetesen a $0<N\leqq 30$ feltételnek kell teljesülnie. N-re a szubrutinban vizsgálatot tartunk és ha az a korlátokon kívülre esik, akkor az átlagértéknek számítás nélkül zérus értéket adunk, és ezt szövegben is kinyomtatjuk. Az átlag számításánál az N-nel való osztáshoz a FLOAT standard utasításfüggvényt használjuk, hogy az egész típusú számból valós típusú legyen. Pl. ha $N=5$, akkor az X=FLOAT(N) hatására $\text{X}=5\mathrm{,}0$ értékű lesz.   A szubrutin egy lehetséges formája az alábbi:   ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{FUNCTION AATL(ADAT,N)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{DIMENSION ADAT(30)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{AATL=O.}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{IF(N)1,1,0}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{IF(N‐30)0,0,4}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{I=1}}\hfill \\ \hfill {\displaystyle \text{ 3}}& \hfill {\displaystyle }\hfill & {\displaystyle \text{AATL=AATL+ADAT(I)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{IF(N‐I)2,2,0}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{I=I+1}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{GO TO 3}}\hfill \\ \hfill {\displaystyle \text{ 2}}& \hfill {\displaystyle }\hfill & {\displaystyle \text{AATL=AATL/FLOAT(N)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{RETURN}}\hfill \\ \hfill {\displaystyle \text{ 4}}& \hfill {\displaystyle }\hfill & {\displaystyle \text{WRITE(3,6)}}\hfill \\ \hfill {\displaystyle \text{ 6}}& \hfill {\displaystyle }\hfill & {\displaystyle \text{FORMAT(//10X,18HN EERTEEKE TUL NAGY)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{RETURN}}\hfill \\ \hfill {\displaystyle \text{ 1}}& \hfill {\displaystyle }\hfill & {\displaystyle \text{WRITE(3,5)}}\hfill \\ \hfill {\displaystyle \text{ 5}}& \hfill {\displaystyle }\hfill & {\displaystyle \text{FORMAT(//10X,23HNINCS MIBOEL AATLAGOLNI)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{RETURN}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{END}}\hfill \end{array}}$   3. feladat. Készítsünk programot, melyben öt koordinátáival adott pont összes lehetséges távolságát és ezek átlagait számítjuk ki a fenti két szubrutin segítségével.   Kinyomtatandók feliratozva az adott öt pont koordinátái, ugyancsak feliratozva a pontok közötti lehetséges távolságok és végül újabb felirat mellett a távolságok átlaga.   Megoldás. Nagyon fontos megjegyzések:   ‐ ha a szubrutin a hívóprogramtól tömböt vesz át, akkor az átadandó tömbnek a hívóprogramrészben is deklaráltnak kell lennie; ‐ a hívóprogramban deklarált tömb mérete nem lehet kisebb, mint a szubrutin által átvett tömbé.   Jelen esetben pl. csak tíz adat átlagát kívánjuk számítani (mivel öt pontnak tíz távolsága lehetséges), a MASTER programrészben mégis 30 elemű vektort kell deklarálnunk, mivel a szubrutin ilyen méretű tömböt ,,vár el''. A távolságokat négy csoportban számítjuk: először a $P_1$ pont távolságát vesszük a másik négy ponttól, azután a $P_2$-ét a többi, nála nagyobb indexű három ponttól, majd a $P_2$ pont távolságát $P_4$ és $P_5$-től, végül a $P_4$ távolságát $P_5$-től.   A távolságokat a D(I) tömbbe helyezzük el éspedig 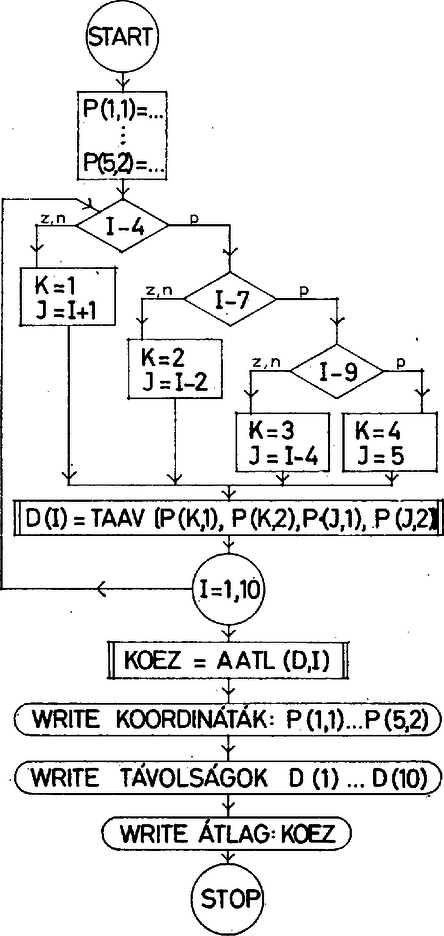  ${\displaystyle \begin{array}{cc}{\displaystyle 1\leqq 1\leqq 4}\hfill & {\displaystyle \text{esetén az első csoport}\mathrm{,}}\hfill \\ {\displaystyle 5\leqq 1\leqq 7}\hfill & {\displaystyle \text{esetén a második csoport}\mathrm{,}}\hfill \\ {\displaystyle 8\leqq 1\leqq 9}\hfill & {\displaystyle \text{esetén a harmadik csoport és}}\hfill \\ {\displaystyle \phantom{8\leqq }1\leqq 10}\hfill & {\displaystyle \text{esetén a negyedik csoport}}\hfill \end{array}}$ távolságait.     A programban a csoport számozását a K azonosító jelenti. A $P_1$, $P_2$ stb. pontok koordinátáit programunkban egyszerű értékadással határozzuk meg és egy 5-ször 2-es méretű tömbbe töltjük be. J a második pont koordinátáihoz tartozó index. A program blokkdiagramja az 1. ábrán, és egy lehetséges megírása az alábbiakban látható.   ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{MASTER PKIL1}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{REAL KOEZ}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{DIMENSION P(5,2),D(30)}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{P(1,1)=5.1}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{P(1,2)=3.7}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{P(2,1)=-1.2}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{P(2,2)=6.3}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{P(3,1)=-7.5}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{P(3,2)=3.4}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{P(4,1)=-4.6}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{P(4,2)=-4.4}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{P(5,1)2.1}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{P(5,2)=-3.9}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{DO 1 I=1,10}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{IF(I‐4)0,0,2}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{K=1}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{J=I+1}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{GO TO 1}}\hfill \\ \hfill {\displaystyle \text{ 2}}\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{IF(I‐7)0,0,3}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{K=2}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{J=I‐2}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{GO TO 1}}\hfill \\ \hfill {\displaystyle \text{ 3}}\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{IF(I-9)0,0,4}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{K=3}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{J=I‐4}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{GO TO 1}}\hfill \\ \hfill {\displaystyle \text{ 4}}\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{K=4}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{J=5}}\hfill \\ \hfill {\displaystyle \text{ 1}}\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{D(I)=TAAV<math xmlns="http://www.w3.org/1998/Math/MathML"></math>(P(K,1),P(K,2),P(J,1),P(J,2)<math xmlns="http://www.w3.org/1998/Math/MathML"></math>)}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{KOEZ=AATL(D,I)}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{WRITE(3,5)}}\hfill \\ \hfill {\displaystyle \text{ 5}}\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{FORMAT(1H1////20X,14HKOORDINAATAAK:/)}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{WRiTE(3,6)(<math xmlns="http://www.w3.org/1998/Math/MathML"></math>(I,P(1,1),I,P(I,2)<math xmlns="http://www.w3.org/1998/Math/MathML"></math>),I=1,5)}}\hfill \\ \hfill {\displaystyle \text{ 6}}\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{FORMAT<math xmlns="http://www.w3.org/1998/Math/MathML"></math>(5(22X,1HX,I1,1H=,F6.3,3X,1HY,I1,1H=,F6.6,/)<math xmlns="http://www.w3.org/1998/Math/MathML"></math>)}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{WRITE(3,7)}}\hfill \\ \hfill {\displaystyle \text{ 7}}\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{FORMAT(///20X,13HTAAVOLSAAGOK:)}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{WRITE(3,8)<math xmlns="http://www.w3.org/1998/Math/MathML"></math>((I,D(I)<math xmlns="http://www.w3.org/1998/Math/MathML"></math>),I=1,10)}}\hfill \\ \hfill {\displaystyle \text{ 8}}\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{FORMAT(10<math xmlns="http://www.w3.org/1998/Math/MathML"></math>(/22X,2HD(,12,3H)=,F10.3)<math xmlns="http://www.w3.org/1998/Math/MathML"></math>)}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{WRITE(3,9)KOEZ}}\hfill \\ \hfill {\displaystyle \text{ 9}}\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{FORMAT(///20X,21HTAAVOLSAAGOK AATLAGA:,F10.3)}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{STOP}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{END}}\hfill \end{array}}$   4.3 A SUBBROUTINE nevű szubrutin   A FUNCTION-hoz abban hasonlít, hogy ‐ az őt hívó programrésztől független programrész; ‐ egy azonosítója van, mely után zárójelben formális paraméterek állnak; ‐ ugyanúgy megkülönböztetünk benne logikai végződést, amelyből többet is tartalmazhat (RETURN) és fizikai végződést, melyből mindig pontosan egy van (END); ‐ a benne szereplő tömböket, illetőleg azonosítókat az előírt módon külön deklarálni kell.   Lényeges különbség a kétfajta szubrutin között, hogy ‐ a SUBROUTINE-t a hívóprogramban külön utasítás hívja be, melyről a legközelebbi rovatunkban lesz szó; ‐ a SUBROUTINE azonosítója nem vesz fel számértéket, a kiszámított eredményt, illetőleg eredményeket az aktuális paraméterek tartalmazzák.   Az alábbi programrész első sora egy szubrutin nyitó utasítása:   ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{SUBROUTINE TRIANG (PONT, OLD, TER)}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{DIMENSION PONT(3,2),OLD(3)}}\hfill \end{array}}$   A zárójelben álló azonosítókról nem látható, hogy azok tömb vagy szám azonosítói. A második sorban levő deklaráció nyújt erre információt. A zárójelben álló azonosítók közül nem mindegyiknek kell értéket adnunk a szubrutin hívása előtt. Elképzelhető például, hogy a PONT három soros két oszlopos mátrix, amely egy háromszög csúcspontjainak koordinátáit tartalmazza és aktuális paraméterként ezt adjuk át a szubrutinnak. Ezekből az kiszámítja az oldalak hosszát, amelyeket az OLD azonosítójú három komponensű vektorban helyez el, a TER azonosítónak pedig a terület mérőszámát adja. Ebben az esetben az OLD és a TER csak a szubrutin végrehajtása után rendelkezik a kívánt aktuális értékekkel. A hívóprogram ezeket fogja átvenni.   Példa. Készítsünk szubrutint, amely a háromszög csúcspontjainak koordinátáiból kiszámítja a magasságvonalak hosszát és a magasságpont koordinátáit. A háromszögben csak abban az esetben érdemes a számítást elvégezni, ha a három pont nem esik egy egyenesbe, azaz ha a   ${\displaystyle \begin{array}{|ccc|}\hline {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>x</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow></math>}}\hfill & {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>y</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow></math>}}\hfill & {\displaystyle \text{ 1}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow></math>}}\hfill & {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>y</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow></math>}}\hfill & {\displaystyle \text{ 1}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>x</mi></mrow><mrow><mn>3</mn></mrow></msub></mrow></math>}}\hfill & {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>y</mi></mrow><mrow><mn>3</mn></mrow></msub></mrow></math>}}\hfill & {\displaystyle \text{ 1}}\hfill \\ \hline\end{array}}$   determináns értéke nem zérus. (Scharnitzky: Mátrix számítás 76. old.) Ezt megvizsgáljuk, és ha zérus, akkor a kimenő adatokat nem számítjuk, hanem az N egész típusú azonosítónak 1 értéket adunk. Ellenkező esetben $N=0$ lesz, és a számítást elvégezzük. Bevezetjük az $\begin{array}{c}{\displaystyle x_i-x_j=u_j\text{és}{y}_i-y_j=v_j}\end{array}$ jelöléseket, ahol $i=1$, 2, 3 esetén $j=2$, 3, 1 értékeket veszi fel rendre. A magasságvonalak talppontjainak $Ti\left(\tilde{x}i\mathrm{,}\tilde{y}i\right)$ koordinátáit az alábbi képletek adják: ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\tilde{x}}_i=\frac{u_j\cdot v_j}{u_j^2+v_j^2}\left(\frac{v_j}{u_j}\cdot x_j+\frac{u_j}{v_j}\cdot x_i+v_i\right)}\hfill \\ \hfill {\displaystyle {\tilde{y}}_i=\frac{u_j\cdot v_j}{u_j^2+v_j^2}\left(\frac{u_j}{v_j}\cdot y_j+\frac{v_j}{u_j}\cdot y_i+u_i\right)}\hfill \end{array}}$ ahol $i=1$, 2, 3 értékek mellett $j=2$, 3, 1. Ezek a képletek azonban csakis akkor használhatók, ha $u_j\ne 0$ és $v_j\ne 0$. $u_j=0$ esetében ${\tilde{x}}_i=x_j$, ${\tilde{y}}_i=y_i$; $v_j=0$ esetében pedig ${\tilde{x}}_i=x_i$ és ${\tilde{y}}_i=y_j$. Ezek után a $P_i$ pontból húzott magasságvonal hossza ($i=1$, 2, 3): $\begin{array}{c}{\displaystyle D_i=\sqrt[]{{\left(x_i-{\tilde{x}}_i\right)}^2+{\left(y_i-{\tilde{y}}_i\right)}^2}\mathrm{.}}\end{array}$ Az $M\left(x\mathrm{,}y\right)$ magasságpont koordinátáit az alábbi képletek adják: ${\displaystyle \begin{array}{c}\hfill {\displaystyle x=\frac{u_j\cdot v_k\cdot x_i-u_k\cdot v_j\cdot x_j+v_i\cdot v_j\cdot v_k}{u_j\cdot v_k-u_k\cdot v_j}}\hfill \\ \hfill {\displaystyle y=\frac{u_k\cdot v_j\cdot y_i-u_j\cdot v_k\cdot y_j+u_i\cdot u_j\cdot u_k}{u_k\cdot v_j-u_j\cdot v_k}}\hfill \end{array}}$ ahol az indexek $i=1$, 2, 3 mellett $j=2$, 3, 1 és $k=3$, 1, 2 értékeket vehetik fel rendre. Természetesen elegendő $i$, $j$ és $k$ egyféle számhármasával számolnunk. Szubrutinunk a hívóprogramtól a CS azonosítójú háromsoros, kétoszlopos tömböt veszi át. Ez soronként tartalmazza a háromszög csúcspontjainak $x$ és $y$ koordinátáit. A hívóprogramban gondoskodunk arról, hogy az egymás alatti sorokban a koordináták a háromszög csúcspontjainak bal irányú körüljárása szerint következzenek. A többi azonosító értéke (VON, MP, N) a hívás pillanatában érdektelen, mivel a SUBROUTINE MAGAS fog értéket adni nekik. Mivel a MP tömb automatikusan egész típusú lenne, azért azt külön REAL-lal deklaráltuk. Szubrutinunkban további, az aktuális paraméterek közt nem szereplő tömbökre is szükség van, melyeket ugyancsak deklaráltunk. A tömbök értelme: VON a magasságvonalak hosszát, MP a magasságpont koordinátáit tartalmazza. U és V a korábbi számításban már bevezetett $u$ és $v$ változóknak felelnek meg, XH és YH a talppontok koordinátáit jelölik. A zérusra való vizsgálat ebben a programunkban is zérus bizonyos környezetébe eső számokra történő vizsgálatot jelent. A szubrutin egy lehetséges megírása az alábbi:   ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{SUBROUTINE MAGAS(CS,VON,MP,N)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{DIMENSION CS(3,2), VON(3), U(3), V(3), XH(3), YH(3)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{REAL MP(2)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{DET=CS(1,1)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>Cs(2,2)+CS(1,2)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>CS(3,1)+CS(2,1)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>CS(3,2)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{DET=DET‐CS(3,1)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>CS(2,2)‐CS(3,2)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>CS(1,1)‐CS(2,1)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>CS(1,2)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{IF(ABS<math xmlns="http://www.w3.org/1998/Math/MathML"></math>(DET‐10.<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo><mo>*</mo></math>(-6)<math xmlns="http://www.w3.org/1998/Math/MathML"></math>)0,0,1}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{N=1}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{RETURN}}\hfill \\ \hfill {\displaystyle \text{ 1}}& \hfill {\displaystyle }\hfill & {\displaystyle \text{N=0}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{DO 2 I=1,3}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{IF(I‐3)0,3,3}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{U(I)=CS(I,1)‐CS(I+1,1)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{V(I)=CS(I,2)‐CS(I+1,2)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{GO TO 2}}\hfill \\ \hfill {\displaystyle \text{ 3}}& \hfill {\displaystyle }\hfill & {\displaystyle \text{U(I)=CS(I,1)‐CS(I‐2,1)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{V(I)=CS(I,2)‐CS(I‐2,2)}}\hfill \\ \hfill {\displaystyle \text{ 2}}& \hfill {\displaystyle }\hfill & {\displaystyle \text{CONTINUE}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{DO 4 1=1,3}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{IF(I‐2)0,8,9}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{J=2}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{GO TO 7}}\hfill \\ \hfill {\displaystyle \text{ 8}}& \hfill {\displaystyle }\hfill & {\displaystyle \text{J=3}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{GO TO 7}}\hfill \\ \hfill {\displaystyle \text{ 9}}& \hfill {\displaystyle }\hfill & {\displaystyle \text{J=1}}\hfill \\ \hfill {\displaystyle \text{ 7}}& \hfill {\displaystyle }\hfill & {\displaystyle \text{IF<math xmlns="http://www.w3.org/1998/Math/MathML"></math>(ABS U(J)<math xmlns="http://www.w3.org/1998/Math/MathML"></math>)‐0.001)11,11,0}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{IF(ABS<math xmlns="http://www.w3.org/1998/Math/MathML"></math>(V(J)<math xmlns="http://www.w3.org/1998/Math/MathML"></math>)‐0.001)10,10,0}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{Z=U(J)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>V(J)/(U(J)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo><mo>*</mo></math>2+V(J)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo><mo>*</mo></math>2)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{XH(I)=Z<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math><math xmlns="http://www.w3.org/1998/Math/MathML"></math>(V(J)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>CS(J,1)/U(J)+U(J)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>CS(I,1)/V(J)+V(I)<math xmlns="http://www.w3.org/1998/Math/MathML"></math>)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{YH(I)Z<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math><math xmlns="http://www.w3.org/1998/Math/MathML"></math>(U(J)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>CS(J,2)/V(J)+V(J)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>CS(I,2)/U(J)+U(I)<math xmlns="http://www.w3.org/1998/Math/MathML"></math>)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{GO TO 4}}\hfill \\ \hfill {\displaystyle \text{ 11}}& \hfill {\displaystyle }\hfill & {\displaystyle \text{XH(I)=CS(J,1)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{YH(I)=CS(I,2)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{GO TO 4}}\hfill \\ \hfill {\displaystyle \text{ 10}}& \hfill {\displaystyle }\hfill & {\displaystyle \text{XH(I)=CS(I,1)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{YH(I)=CS(J,2)}}\hfill \\ \hfill {\displaystyle \text{ 4}}& \hfill {\displaystyle }\hfill & {\displaystyle \text{VON(I)=SQRT(<math xmlns="http://www.w3.org/1998/Math/MathML"></math>(CS(1,1)‐XH(I)<math xmlns="http://www.w3.org/1998/Math/MathML"></math>)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo><mo>*</mo></math>2+<math xmlns="http://www.w3.org/1998/Math/MathML"></math>(CS(1,2)‐YH(I)<math xmlns="http://www.w3.org/1998/Math/MathML"></math>)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo><mo>*</mo></math>2)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{MP(1)=U(2)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>V(3)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>CS(1,1)‐U(3)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>V(2)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>CS(2,1)+V(1)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>V(2)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>V(3)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{MP(1)=MP(1)/<math xmlns="http://www.w3.org/1998/Math/MathML"></math>(U(2)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>V(3)‐U(3)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>V(2)<math xmlns="http://www.w3.org/1998/Math/MathML"></math>)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{MP(2)=U(3)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>V(2)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>CS(1,2)‐U(2)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>V(3)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>CS(2,2)+U(1)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>U(2)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>U(3)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{MP(2)=MP(2)/<math xmlns="http://www.w3.org/1998/Math/MathML"></math>(U(3)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>V(2)‐U(2)<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>*</mo></math>V(3)<math xmlns="http://www.w3.org/1998/Math/MathML"></math>)}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{RETURN}}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle \text{END}}\hfill \end{array}}$   Feladat   Szubrutin készítendő, amely tetszőleges konvex négyszög csúcspontjainak koordinátáiból kiszámítja annak területét és kerületét. A bal körüljárás szerint következő csúcspontok koordinátáit egy mátrix egymás alatti sorai tartalmazzák. A szubrutin megfelelő értelmű szöveg nyomtatásával jelezze, ha a négy pont vagy közülük bármelyik három egy egyenesbe esik. Ilyen esetekben a területet, kerületet ne számolja.