Kezdőlap


Cím:	Számítástechnikai rovat (3)
Füzet:	1976/december, 216 - 221. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az októberi számban a következő feladatot tűztük ki.
Feladat. Készítsünk programot, amely kinyomtat egy sakktáblát úgy, hogy azon a fekete négyzeteket X betűkkel töltjük ki. Egy négyzet egy sorban hat karakterpozícióból álljon, és egymás alatt négy ilyen sor legyen. A 6-szor 4 karakter alkot egy négyzetet. A sakktábla a papírlap közepére kerüljön.
A feladatnak egy lehetséges megoldása az alábbi. A sakktábla a kikötés értelmében soronként 48 karakterből áll és 32 ilyen sor kerül egymás alá. Tudjuk, hogy soronként 128 karakter nyomtatható és egy lapon 72 sor fér el. Hogy a lap közepére kerüljön a tábla, ezért a 21. sorban kezdjük el a nyomtatást és a sorban az első karakterek a 41. pozícióra kerülnek. Ezek alapján a program

\begin{matrix} MASTER SAKK \\ WRITE (3,10) \\ WRITE (3,11) \\ 10 & FORMAT (1H1,20(/)) \\ 11 & FORMAT (4(4(40X,4(12HXXXXXX▿ ▿ ▿ ▿ ▿ ▿)/), \\ 4(40X,4(12H▿ ▿ ▿ ▿ ▿ ▿)/) XXXXXX)/))) \\ STOP \\ END \end{matrix}

(A második FORMAT utasítás a programlapon egy sorba írandó, itt csak helyszűke miatt törtük meg két sorba.)
A feladat látszólag bonyolult nyomtatási képét egy igen egyszerű programmal valósítottuk meg. Ha valaki DO utasítást is használt, attól a program még lehet hibátlan, de a végrehajtás ideje így hosszabb.
A rövid programírásra az adott lehetőséget, hogy a nyomtatandó karaktereket eleve meg tudtuk adni, azok nem képezték számítás tárgyát. Ezzel lezártuk a részünkre szükséges specifikációk tárgyalását.

3.4. Belső ciklus a WRITE-ban

Tekintsük a következő feladatot:

Kiszámíttatjuk és kinyomtatjuk a

2 x^{3} + 3 y^{3} - 4 x^{2} y - 5 x y^{2} + 6 x^{2} - 7 y^{2} +

+ 8 x y - 9 x + 10 y + 11

kétváltozós harmadfokú polinom helyettesítési értékeit két tizedesjegy pontossággal a

\begin{matrix} - 3 \leq x \leq + 3 \end{matrix}

és

\begin{matrix} - 6 \leq y \leq + 6 \end{matrix}

értékhatárok között, miközben a lépésközök:

\begin{matrix} Δ x = 0, 2 és Δ y = 1. \end{matrix}

A két változó értékének változtatása mellett a helyettesítési értékek egy számtáblázatban, ún. mátrixban helyezhetők el. A feladat szerint

x

összesen 31,

y

összesen 13 értéket kap. A táblázatban tehát 13-szor 31 adat lesz. Nyilván célszerű a táblázatot a papírra úgy nyomtatni, hogy az oszlopok száma legyen 13 és a soroké 31. Ha 13 szám van egy sorban, akkor egy adat legfeljebb 9 karakterpozíción helyezkedhet el. Az áttekinthetőség érdekében két szám között legalább egy karakterpozíciót kell üresen hagyni, emiatt egy adat legfeljebb 8 pozíción helyezkedhet el. Figyelembe véve az előjel, a tizedespont és a két tizedes jegy helyét, az egész rész legfeljebb négy értékes jegyet tartalmazhat. Kérdéses, hogy a számítandó értékek elférnek-e egy ilyen mezőben. Ezt természetesen előre nem tudhatjuk, és ilyen esetekre a programozónak megfelelő becsléseket kell tudnia tenni. Mi azonban a bonyolultság csökkentése érdekében most előre közöljük, hogy jelen esetben ez nem okoz gondot. A kívánt nyomtatási kép tehát kialakítható.

A programot két részből állítjuk össze. Az első részben betöltjük a Z(I, J) mátrixba (kétdimenziós tömbbe) az adatokat. A program másik részében kinyomtatjuk a mátrixot. A számítási és a nyomtatási részt általában célszerű különálló programrészekben megírni, mert ezzel a gép kihasználása gazdaságosabb, a program végrehajtásának ellenőrzése könnyebb.

A blokkdiagramot az 1. ábrán láthatjuk. Ezen, a DO ciklusokat nagy, köralakú blokkok jelképezik.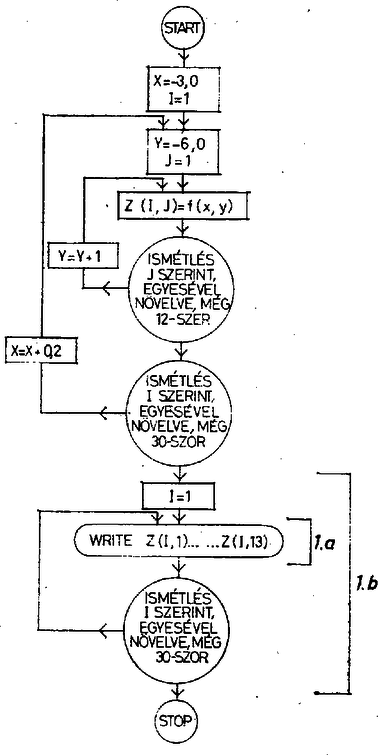

Tartalmukat az 1. ábrán részletesen szöveggel Írtuk ki, de a továbbiakban már csak a DO utasítás megfelelő részét írjuk majd bele, pl. J=1,13 stb. Az ábrán a Z(I, J) mátrix értékadásánál a feladatban adott polinomot röviden

f (x, y)

-nal jelöltük.

A blokkdiagram alapján a program pl. ilyen lehet:

\begin{matrix} MASTER PKET \\ DIMENSION Z(31,13) \\ X=-3.0 \\ DO 1 I=1,31 \\ Y=-6.0 \\ DO 2 J=1,13 \\ Z(I,J)=X*(X*(2*X-4*Y+6)-9)+Y*(Y*(3*Y-5*X-7)+8*X+10)+11 \\ 2 & Y=Y+1 \\ 1 & X=X+0.2 \\ DO 3 I=1,31 \\ 3 & WRITE (3,9) Z (I,1), Z(I,2), Z(I,3), Z(I,4), Z(I,5) Z(I,6) \\ Z(I,7), Z(I,8), Z(I,9), Z(I,10), Z(I,11),  Z(I,12), Z(I,13) \\ 9 & FORMAT (9X, 13F9.2) \\ STOP \\ END \end{matrix}

A WRITE utasítás után álló hosszú lista kényelmetlen a sok írás miatt, és egy programsorban el sem fér (mi is két sorba törtük meg a helyszűke miatt). Ezért bemutatunk egy újabb lehetőséget, a WRITE utasításba épített ciklust. Ennek formája a következő:

\begin{matrix} 3 & WRITE (3,9)(Z(I,J), J=1,13) \end{matrix}

Az így felírt utasítás hatására az egy sorba eső elemek kerülnek kinyomtatásra oly módon, hogy I értéke állandó marad, J értéke 1-től 13-ig növekszik. I értéke természetesen a DO ciklus minden egyes menetében emelkedik. Ennek bemutatására szolgálhat az 1. ábra. Megjegyezzük azonban, hogy az 1.a és 1.b ábrákon látható WRITE blokk nem használatos, csak itt rajzoltuk meg a könnyebb elképzelhetőség érdekében.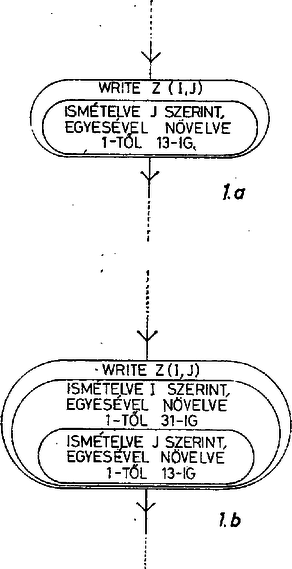

Gyakorlatban a nyomtatási blokkba csak a WRITE Z (I, j) beírása történik, és a programblokkban nem tüntetjük fel a nyomtatás technikai megszervezését.
Van azonban arra is mód, hogy az egész mátrix nyomtatását egy utasítással hajtsuk végre. Ha programunkat módosítjuk és az 1-es címkéjű utasítástól kezdve az alábbi módon írjuk:

\begin{matrix} 1 & X=X+0.2 \\ 3 & WRITE (3,9) ((Z(I,J), J=1,13), 1=1,31) \\ 9 & FORMAT (31(9X,13F9.2/)) \\ STOP \\ END \end{matrix}

akkor a WRITE-ba építhető ciklusokat ebben a feladatban teljes mértékben kihasználtuk. A FORMAT belső zárójelében foglaltak szerint történik egy‐egy sor nyomtatása, itt azonban már elő kell írni a sorváltást is. Ennek a szemléltetésére szolgálhat az 1.b ábrán bemutatott blokk.

Feladat:

Vizsgáljuk meg, hogy miként változik az előző példában adott polinom teljes értéktáblázata, ha valamennyi együtthatójának értékét egyidejűleg azok 150

%

-ára növeljük.
Kinyomtatandó az eredeti polinom értéktáblázata, a megnövelt együtthatójú polinom értéktáblázata, valamint a megnövelt együtthatójú polinom értéktáblázatának és az eredeti polinom értéktáblázatának különbsége.

Ehhez magyarázatul a következőt fűzzük:

Az eredeti feladat egy olyan eredménymátrixot szolgáltatott, melynek 31 sora és 13 oszlopa volt. Jelöljük most ezt a táblázatot így:

\begin{matrix} [\begin{matrix} a_{1,1} & a_{1,2} & ... ... ... ... ... & a_{1,12} & a_{1,13} \\ a_{2,1} & a_{2,2} & ... ... ... ... ... & a_{3,12} & a_{2,13} \\ ⋮ & ⋮ \\ a_{30,1} & a_{30,2} & ... ... ... ... ... & a_{30,12} & a_{30,13} \\ a_{31,1} & a_{31,2} & ... ... ... ... ... & a_{31,12} & a_{31,13} \end{matrix}] = {[a_{i, j}]}_{31 \times 13} \end{matrix}

Általános szokás, hogy az első index a sort, a második az oszlopot jelöli. A mátrixokat nagy szögletes zárójelbe szoktuk írni. A mátrix mellett jobb oldalt annak egy egyszerűsített jelölése látható, melyben

i

és

j

futóindexek, ahol

\begin{matrix} 1 \leq i \leq 31 és 1 \leq j \leq 3. \end{matrix}

A kitűzött feladatban (az együtthatók növelése miatt) új eredményeket is kapunk. Jelöljük most ezek mátrixát így:

\begin{matrix} {[b_{i, j}]}_{31 \times 13} . \end{matrix}

A feladat a "táblázatok különbségének'', azaz a különbségmátrixnak a kinyomtatását is előírja. Ezt a különbséget részletesen így írjuk fel:

\begin{matrix} [\begin{matrix} b_{1,1} & - a_{1,1} & ... ... ... ... ... & b_{1,13} & - a_{1,13} \\ b_{2,1} & - a_{2,1} & ... ... ... ... ... & b_{2,13} & a_{2,13} \\ ⋮ & ⋮ \\ b_{30,1} & - a_{30,1} & ... ... ... ... ... & b_{30,13} & - a_{30,13} \\ b_{31,1} & - a_{31,1} & ... ... ... ... ... & b_{31,13} & - a_{31,13} \end{matrix}] = {[b_{i, j} - a_{i, j}]}_{31 \times 13} \end{matrix}

A programhoz tartozó blokkdiagramot itt nem közöljük. A programban deklarálnunk kell három darab kétdimenziós és két darab egydimenziós tömböt. A Z tömb az eredeti polinom, a V tömb a növelt együtthatójú polinom értéktáblázatát és a W tömb a különbségmátrixot fogja tartalmazni. Az A tömb az eredeti együtthatókat, a B pedig a 150

%

-ra megnövelt együtthatókat tartalmazza. A program elején kihasználjuk, hogy az együtthatók abszolút értékei egyesével növekednek, amit az A tömb betöltésénél láthatunk. A polinomot tartalmazó értékadó utasítást a helyszűke miatt két sorra bontottuk fel.
Érdekessége a programnak, hogy ugyanaz a FORMAT utasítás három WRITE utasításhoz tartozik. A programban meglehetős kényelmetlen, hogy lényegében ugyanezt a polinomot tartalmazó két értékadó utasítást úgy kellett felírni, hogy mindegyikben kiírtuk az egész polinomot. Következő számunkban látni fogjuk, hogy ilyen esetekben hogy tudjuk egyszerűbbé tenni a programírást.
Ezek után a program az alábbi:

\begin{matrix} MASTER PHAR \\ DIMENSION Z(31,13), V(31,13), W(31,13), A(10), B(10) \\ R=2.0 \\ DO 4 K=1,10 \\ A(K)=R \\ B(K)=1.5*A(K) \\ 4 & R=R+1 \\ X=-3.0 \\ DO 1 I=1,31 \\ Y=-6.0 \\ DO 2 J=1,13 \\ Z(I,J)=X*(X*(A(1)*X-A(3)*Y+A(5))-A(8)) \\ Z(I,J)=Z(I,J)+Y*(Y*(A(2)*Y-A(4)*X-A(6))+A(7))*X+A(9)) \\ +A(10) \\ V(I,J)=X*(X*(B(1)*X-B(3)*Y+B(5))-B(8)) \\ V(I,J)=V(I,J)+Y*(Y*(B(2)*Y-B(4)*X-B(6))+B(7))*X+B(9)) \\ +B(10) \\ W(I,J)=V(I,J)-Z(I,J) \\ 2 & Y=Y+1 \\ 1 & X=X+0.2 \\ WRITE (3,3) \\ 3 & FORMAT(1H1//10X,25HEREDETI EERTEKTAABLAAZAT) \\ WRITE(3,9)((Z(I,J), J=1,13), I=1,13) \\ WRITE(3,5) \\ 5 & FORMAT(1H1//10X,32H150%-OSAN NOEVELT EGYUET- \\ HATOOVAL) \\ WRITE(3,9)((V(I,J), J=1,13), I=1,31) \\ WRITE(3,6) \\ 6 & FORMAT(1H1//10X,19HKUELOEBSEG MATRIX) \\ WRITE(3,9)((W(I,J), J=1,13), I=1,31) \\ 9 & FORMAT(//31 (9X,13F9.2/)) \\ STOP \\ END \end{matrix}

Feladat

1. A Számítástechnikai Rovat 1. sz. feladatát, melyben egy sorban kellett kinyomtatni a természetes számokat, ismételjük meg a következő kikötésekkel:

a) a számok 91-től növekedjenek egyesével,

b) a program WRITE utasításba épített ciklussal készüljön.

2. a) Készítsünk programot, amely a

\begin{matrix} 2 x^{3} - 4 y^{3} + 6 x^{2} - 8 x y + 10 y - 12 \end{matrix}

polinomnak három tizedesjegy pontossággal kinyomtatja a helyettesítési értéktáblázatát a

\begin{matrix} - 1 \leq x \leq + 1 és - 12 \leq y \leq + 12 \end{matrix}

határok között,

Δ x = 0, 2

és

Δ y = 0, 5

lépésközök mellett.
b) Bővítsük e feladatot úgy, hogy a fenti mátrixon kívül nyomtassa még annak a polinomnak a helyettesítési értéktáblázatát, melyet az adott polinomból úgy nyerünk, hogy valamennyi együttható értékét egyidejűleg 1-gyel csökkentjük.
Ezután nyomtassa még ki a program azt a mátrixot, mely százalékban kifejezve megmutatja, hogy a csökkentett együtthatóval képzett helyettesítési értékek az eredeti polinom helyettesítési értékeinek hány százalékai. Vegyük figyelembe, hogy az eredeti polinom helyettesítési értékei között 0 is lehet.
Ehhez az anyagrészhez tartozó utalás LV: 225. oldalon és 265. oldalon található.

A feladatokat a következő címre küldjék a megoldók:

MÜM Számítástechnika Intézet
Gergely János
1089 Budapest

Reguly Antal u. 57‐59.