| Cím: | A szófogadó legyek, avagy néhán szó a spirálisokról | |
| Szerző(k): | Csirmaz László | |
| Füzet: | 1976/december, 213 - 214. oldal |  PDF | MathML PDF | MathML |
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A szófogadó legyek, avagy néhány szó a spirálisokról Hat legyet egy szabályos hatszög csúcsaiba teszünk, és "meghagyjuk'' nekik, hogy egyforma, állandó sebességgel haladjanak a jobb oldali szomszédjuk felé. Mennyi idő múlva találkoznak? Hátsó borítónkon a legyek útjának egy részét rajzoltuk fel. 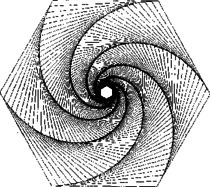 Látjuk, hogy a hatszög középpontját járják körbe, ahhoz egyre közelebb kerülnek és végül a középpontban találkoznak. A találkozásig kétszer akkora utat kell megtenniük, mint amekkora a hatszög egy oldala. Az útvonaluk úgynevezett logaritmikus spirális. Egy kutató az Északi‐sarkról elindul, és egyenesen halad Dél felé. Milyen útvonalon halad? Természetesen egyenesen; ám ez csak akkor igaz, ha a Földdel együtt forogva figyeljük a gyalogost. Ha viszont egy, az Északi‐sark fölött lebegő űrhajóból nézzük, és az űrhajó mozdulatlanul áll, azaz nem forog a Földdel együtt, akkor a pályát olyannak látjuk, amilyet az 1. ábra mutat. 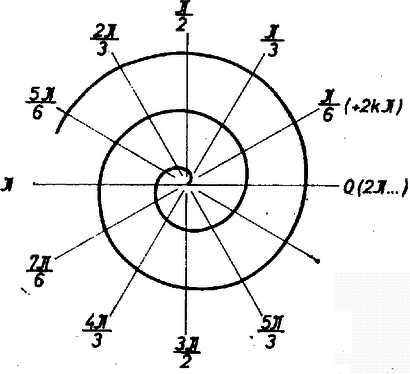 1. ábra Ugyanilyen pályán mozog az a kisegér, amelyik egy forgó korong közepétől annak a széléig szalad. Az útvonal neve archimédeszi spirális. Ezeknek a spirálisoknak természetesen egyenletük is van, mint ahogyan van egyenlete a körnek, egyenesnek, ellipszisnek is. A szokásos derékszögű koordináta‐rendszer nem a legalkalmasabb a spirálisok egyenletének felírására, ezért bevezetünk egy másik koordináta‐rendszert, az ún. polárkoordináta‐rendszert (poláris=sarki) a következőképpen: az irányított síkban egy kezdőpontú félegyenest választunk, amelynek irányát kezdőiránynak nevezzük. Egy pontot most is két adat határoz meg: az ponttól való távolsága (ezt általában -rel jelöljük) és az félegyenesnek a kezdőiránnyal bezárt irányított szöge (amit -vel jelölünk; 2. ábra). 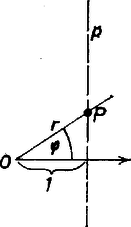 2. ábra Például az középpontú, egységsugarú kör egyenlete ebben a koordináta‐rendszerben ; egyenletű alakzat pedig egy "függőleges'' egyenes. A polárkoordináták bevezetésével a spirálisok egyenletei igen egyszerűen alakulnak. Az archimedeszi spirális egyenlete: , itt tetszőleges állandót jelöl. Az archimedeszi spirális a legegyszerűbb spirálisok egyike. A logaritmikus spirálisnak (a legyek útvonalának) egyenlete (, állandók, ) a természetes logaritmus alapszáma). A hátsó borítón található spirálisok egyenlete ‐ amennyiben a hatszög oldalát választjuk egységnyinek ‐ alakú lesz. Ez a spirális elnevezését is egyenlete után kapta. Érdekes tulajdonsága, hogy minden pontjában az érintő és a pontot az -val összekötő egyenes ugyanakkora szöget zár be; ez az egyetlen ilyen tulajdonságú síkgörbe. Másik érdekessége, hogy egy rögzített pontjából befelé haladva a görbe végtelen sokszor kerüli meg az pontot, de ívhossza véges! Mégpedig, ha a pont távolsága -tól , akkor az ívhossz: . Ha darab szófogadó legyet egy szabályos -szög csúcsaiba teszünk, majd elindítjuk őket, a találkozásukig utat kell megtenniük ( az -szög köré írható kör sugara), hiszen a legyek olyan logaritmikus spirálison mozognak, amelynek szöge . A hajósok vagy pilóták, ha nagy távolságot kell megtenniük, igyekeznek olyan útvonalat választani, hogy az út folyamán az iránytű végig ugyanazt az értéket mutassa. Ez azt jelenti (némi elhanyagolással), hogy a délköröket az útvonal állandó szög alatt metszi. És ha az útvonalat a 3. ábra szerinti térképre rajzolják, akkor az útvonal egy logaritmikus spirális egy ívét adja. 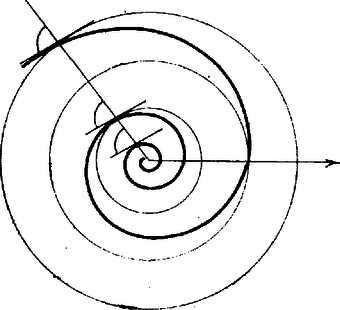 3. ábra (Ezt az útvonalat loxodrómának hívják.) |