Kezdőlap


Cím:	Megoldásvázlatok a 2020/4. szám emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Varga Péter (Budapest)
Füzet:	2020/május, 273 - 284. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. rész

a)

Oldjuk meg a

\sqrt[]{2 x + 6} = 9 - x

egyenletet a valós számok halmazán.
(5 pont)

b)

Oldjuk meg a

log_{0, 3} x \geq log_{0, 3} \frac{4}{9}

egyenlőtlenséget a valós számok halmazán.
(3 pont)

c)

Oldjuk meg a

sin^{2} 4 x + sin 4 x + cos^{2} 4 x = 2

egyenletet a

[0; π]

halmazon.
(4 pont)

Megoldás.

a)

A négyzetgyökfüggvény értelmezési tartománya miatt

x \geq - 3

, értékkészlete miatt

x \leq 9

, tehát

- 3 \leq x \leq 9

. Négyzetre emelve az egyenlet mindkét oldalát:

2 x + 6 = 81 - 18 x + x^{2}

. Az egyenletet rendezve:

x^{2} - 20 x + 75 = 0

, melynek gyökei:

x_{1} = 15

és

x_{2} = 5

.
A

[- 3; 9]

intervallumon ekvivalens átalakításokat végeztünk, így csak

x_{2} = 5

megoldása az egyenletnek.

b)

Az egyenlőtlenség értelmezési tartománya:

x > 0

. A 0,3-es alapú logaritmusfüggvény szigorú monoton csökkenése miatt:

x \leq \frac{4}{9}

, melyet az értelmezési tartománnyal összevetve a megoldáshalmaz:

] 0; \frac{4}{9}]

c)

Mivel minden

x \in R

esetén

sin^{2} 4 x + cos^{2} 4 x = 1

, ezért a megoldandó egyenlet:

sin 4 x = 1

, ahonnan

x = \frac{π}{8} + k \cdot \frac{π}{2}

k \in Z

. Ebből az egyenlet megoldásai a keresett halmazon:

x = \frac{π}{8}; \frac{5 π}{8}

. Ekvivalens átalakításokat végeztünk, ezért ebből következik, hogy a kapott gyökök jók.

2. Adott a derékszögű koordináta-rendszerben az

y + 2 x = x^{2}

egyenletű parabola.

a)

Írjuk fel a parabola

E (2; 0)

pontjában húzott érintő egyenletét. (3 pont)

b)

Számítsuk ki a parabola tengelypontjának koordinátáit és határozzuk meg a parabola paraméterét. (4 pont)
A koordináta-rendszerben a

(- 4; 0)

(4; 0)

(4; 8)

és

(- 4; 8)

csúcspontokkal megadott téglalapot a fenti parabola három részre vágja.

c)

Mekkora a középső rész területe? (6 pont)

Megoldás.

a)

E

-ben húzott érintő meredekségét a parabola deriváltfüggvényének az

x = 2

helyen felvett helyettesítési értéke adja meg.

f' (x) = 2 x - 2

, így az érintő meredeksége

f' (2) = 2

.
Az érintő egyenlete:

y = 2 x - 4

b)

Teljes négyzetté alakítással:

y = {(x - 1)}^{2} - 1

, ahonnan a parabola tengelypontja

T (1; - 1)

. A parabola paraméterére:

\frac{1}{2 p} = 1

, így

p = \frac{1}{2}

c)

A megadott parabola a téglalapot a

(0; 0)

(2; 0)

(4; 8)

és

(- 2; 8)

pontokban metszi. A

[- 2; 0]

intervallumon az

x

tengely és a parabolaív közötti terület nagysága:

\begin{matrix} \int_{- 2}^{0} (x^{2} - 2 x) d x = {[\frac{x^{3}}{3} - x^{2}]}_{- 2}^{0} = - (- \frac{8}{3} - 4) = \frac{20}{3} . \end{matrix}

A parabola tengelyes szimmetriája miatt a

[- 2; 0]

és a

[2; 4]

intervallumokon a parabola alatti terület megegyezik, így a középső táblarész területét megkapjuk, ha egy 48 egység területű téglalapból kivonjuk a

[- 2; 0]

és a

[2; 4]

intervallumhoz tartozó parabola alatti területet. Tehát a keresett terület:

\begin{matrix} T = 48 - 2 \cdot \frac{20}{3} = \frac{104}{3} . \end{matrix}

a)

Egy mértani sorozat

1011

-edik tagja megegyezik a sorozat nullától különböző hányadosával. Számítsuk ki a sorozat első

2019

tagjának a szorzatát. (6 pont)

b)

Jelölje

x

és

y

ebben a sorrendben egy mértani sorozat két egymást követő tagját. Tudjuk, hogy

x \neq 0

és az

(x; y)

számpár megoldása a

\begin{matrix} 100^{x} - 2 \cdot 10^{x} \cdot 10^{2 y} + 10^{4 y} \leq 0 \end{matrix}

egyenlőtlenségnek. Számítsuk ki a sorozat hányadosát. (6 pont)

Megoldás.

a)

I. megoldás. Jelölje a mértani sorozat hányadosát

q

(

q \neq 0

). Ekkor a feladat szövege alapján:

a_{1012} = q^{2}

a_{1013} = q^{3}

...

a_{2019} = q^{1009}

adódik.
Hasonlóan az indexek csökkentésével:

a_{1010} = 1

a_{1009} = \frac{1}{q}

a_{1008} = \frac{1}{q^{2}}

...

a_{1} = \frac{1}{q^{1009}}

.
Az előzőeket felhasználva a keresett szorzat:

\begin{matrix} a_{1} \cdot a_{2} \cdot ... \cdot a_{1009} \cdot a_{1010} \cdot a_{1011} \cdot ... \cdot a_{2018} \cdot a_{2019} = \\ = \frac{1}{q^{1009}} \cdot \frac{1}{q^{1008}} \cdot ... \cdot \frac{1}{q} \cdot 1 \cdot q \cdot ... \cdot q^{1008} \cdot q^{1009} = 1. \end{matrix}

II. megoldás. Jelölje a mértani sorozat első tagját

a_{1}

, hányadosát

q

(

q \neq 0

). Ekkor a sorozat tagjait felírva:

a_{2} = a_{1} \cdot q

a_{3} = a_{1} \cdot q^{2}

...

a_{2019} = a_{1} \cdot q^{2018}

. Az első 2019 tagot összeszorozva a szorzat értéke:

\begin{matrix} a_{1}^{2019} \cdot q^{1 + 2 + 3 + 4 + ... + 2018} = a_{1}^{2019} \cdot q^{2 037 171} . \end{matrix}

A feladat feltétele szerint:

a_{1} \cdot q^{1010} = q

, ahonnan (

q \neq 0

miatt)

a_{1} = \frac{1}{q^{1009}}

. A keresett szorzat:

\begin{matrix} {(\frac{1}{q^{1009}})}^{2019} \cdot q^{2 037 171} = \frac{1^{2019}}{q^{2 037 171}} \cdot q^{2 037 171} = 1. \end{matrix}

b)

Mivel

100^{x} = {(10^{x})}^{2}

és

10^{4 y} = {(10^{2 y})}^{2}

, így

100^{x} - 2 \cdot 10^{x} \cdot 10^{2 y} + 10^{4 y} = {(10^{x} - 10^{2 y})}^{2} \leq 0

{(10^{x} - 10^{2 y})}^{2} \leq 0

pontosan akkor teljesül, ha

10^{x} - 10^{2 y} = 0

, vagyis

10^{x} = 10^{2 y}

, azaz (a 10-es alapú exponenciális függvény szigorú monotonitása miatt)

x = 2 y

. (Mivel

x \neq 0

, ezért)

\frac{y}{x} = \frac{1}{2}

4. A VONALAZÓ nevű játékot két ember játszhatja.
A játék menete
Egy papírlapra a játékosok néhány pontot rajzolnak. A kezdő játékos húz egy vonalat valamelyik pontból egy másik pontig, és a vonalra egy újabb pontot rajzol. Így ebből az új pontból két vonal indul ki. A két játékos felváltva húzza a vonalakat a pontok között és a játékos a megrajzolt vonalra mindig egy új pontot rajzol a következő szabályok betartásával:

$1.$	Mindegyik vonal alakja tetszőleges lehet, de nem metszheti önmagát és nem metszhet egyetlen korábban megrajzolt vonalat sem.

$2.$	Az összekötő vonal két pontot köt össze és nem mehet át más korábban megrajzolt ponton.

$3.$	Két pontot csak egyetlen vonal köthet össze.

$4.$	Egyetlen pontból sem indulhat ki háromnál több vonal.

Az veszít, aki már nem tud húzni egy vonalat sem.

a)

A 4.1. ábrán

3

pont látható. Rajzoljuk bele az ábrába ‐ a fenti feltételek figyelembevételével ‐ annak a játéknak az egyes lépéseit, amelyben pontosan

4

új pont szerepel. A kezdő játékos vonala legyen folytonos, az ellenfélé pedig szaggatott. Az új pontokat üres karikával jelölje. (3 pont)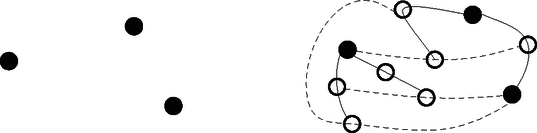

4.1. ábra 4.2. ábra

A 4.2. ábrán egy játszma lépéseit lehet nyomon követni. A kezdő játékos vonalait a folytonos, az ellenfél lépéseit pedig a szaggatott vonalak jelzik.

b)

Számozzuk be az üres karikával jelzett új pontokat a keletkezésük sorrendjében és döntsük el, melyik játékos nyerte a játszmát. (4 pont)
Levente Csabával már nagyon sokszor játszotta a VONALAZÓ nevű játékot. Annak a valószínűsége, hogy Levente

10

játékból legalább

8

-at megnyer kétszer akkora, mint annak, hogy pontosan

8

-at nyer meg. (Tételezzük fel, hogy Levente mindegyik játszmában ugyanakkora valószínűséggel nyer.)

c)

Mennyi annak a valószínűsége, hogy Levente megnyer egy játszmát? (7 pont)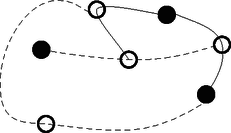

Megoldás.

a)

Egy lehetséges megoldás van a 4.3. ábrán.

4.3. ábra

b)

A 4.4. ábrán látható sorrend miatt a kezdő játékos nyerte a játszmát.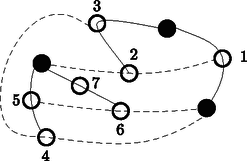

4.4. ábra

c)

Jelölje

p

annak a valószínűségét, hogy Levente megnyer egy játszmát. Ekkor annak a valószínűsége, hogy Csaba nyer

1 - p

.
Annak a valószínűsége, hogy Levente 10-ből pontosan 8-szor nyer:

\begin{matrix} (\binom{10}{8}) \cdot p^{8} \cdot {(1 - p)}^{2} . \end{matrix}

Annak a valószínűsége, hogy Levente 10-ből pontosan 9-szer nyer:

\begin{matrix} (\binom{10}{9}) \cdot p^{9} \cdot {(1 - p)}^{1} . \end{matrix}

Annak a valószínűsége, hogy Levente 10-ből pontosan 10-szer nyer:

\begin{matrix} (\binom{10}{10}) \cdot p^{10} \cdot {(1 - p)}^{0} . \end{matrix}

A feladat szerint:

\begin{matrix} (\binom{10}{8}) \cdot p^{8} \cdot {(1 - p)}^{2} + (\binom{10}{9}) \cdot p^{9} \cdot {(1 - p)}^{1} + (\binom{10}{10}) \cdot p^{10} \cdot {(1 - p)}^{0} = \\ = 2 \cdot (\binom{10}{8}) \cdot p^{8} \cdot {(1 - p)}^{2} . \end{matrix}

Az egyenlet mindkét oldalát elosztva

p^{8}

-nal, és kiszámolva a binomiális együtthatókat:

\begin{matrix} 45 \cdot {(1 - p)}^{2} + 10 p \cdot (1 - p) + p^{2} = 90 \cdot {(1 - p)}^{2} . \end{matrix}

Ebből:

54 p^{2} - 100 p + 45 = 0

, melynek gyökei

p_{1} \approx 1, 081

és

p_{2} \approx 0, 771

.
Mivel a valószínűség legfeljebb 1, így Levente kb. 0,771 valószínűséggel nyer meg egy játszmát.

II. rész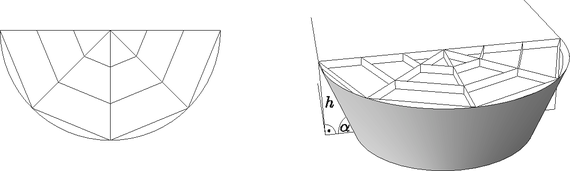

5. Egy zöldségárus a friss áruját a pulton félkörívben helyezi el. Az egyes tartományokat falécek határolják. A félkör az 5.1. ábrán látható módon négy egybevágó körcikkre van osztva. Az ábrán látható összes egyenes szakasz és a félkörív is falécből készült. A szomszédos sugarakat összekötő elválasztó lécek párhuzamosak és három egyenlő részre osztják a sugarakat. A félkör sugara 1,5 méter.

5.1. ábra 5.2. ábra

a)

Hány méter falécre van szükség a pult kialakításához? Válaszunkat egészre kerekítve adjuk meg. (8 pont)
Egy másik zöldségesnek megtetszett az ötlet és bódéjához egy félbevágott csonkakúp alakú bővítményt tervezett az ábra szerint, ahol

h

a bővítmény magasságát,

α

pedig a félbevágott csonkakúp bódéval érintkező alkotójának a bódé alsó, vízszintes élével bezárt szögét jelöli. A bővítmény méretei:

h = 100

cm,

α = 70^{\circ}

, a felső kör sugara pedig 1,5 m (5.2. ábra).

b)

Mennyi anyag szükséges a szürkével jelölt palástrész beborításához, ha az illesztések miatt plusz 4% anyaggal kell számolni? Válaszunkat tized négyzetméterre kerekítve adjuk meg. (8 pont)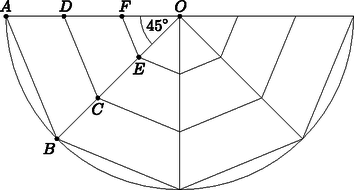

Megoldás.

a)

Az 5.3. ábrán látható félkörív hossza

1, 5 \cdot π \approx 4, 712

(m).

5.3. ábra

Mivel a körcikkek egybevágók, ezért az

A O B ∢ = 45^{\circ}

.
Az

A B

szakasz hosszát koszinusztétellel számolva:

\begin{matrix} A B^{2} = 1, 5^{2} + 1, 5^{2} - 2 \cdot 1, 5 \cdot 1, 5 \cdot cos 45^{\circ}, \end{matrix}

ahonnan

A B \approx 1, 148

(m). Az

O A B

és

O F E

, valamint az

O D C

és

O F E

háromszögek hasonlósága miatt a hasonlóság arányának felhasználásával

\begin{matrix} C D = \frac{2 \cdot A B}{3} \approx 0, 765 (m)   és E F = \frac{A B}{3} \approx 0, 383 (m). \end{matrix}

Mindegyik keresztlécből 4 db van, a sugárból pedig öt, így a keresett hosszúság:

\begin{matrix} 4, 712 + 5 \cdot 1, 5 + 4 \cdot (1, 148 + 0, 765 + 0, 383) = 21, 396 (m). \end{matrix}

Tehát 22 méter falécre van szükség.

b)

Az 5.4. ábra jelöléseit használva az

A T D

derékszögű háromszögben:

tg 70^{\circ} = \frac{100}{x}

, ahon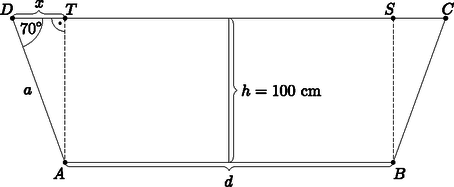nan

x \approx 36, 40

(cm), és

sin 70^{\circ} = \frac{100}{a}

, melyből

a \approx 106, 42

(cm).

5.4. ábra

Az előbbiek miatt

d = 300 - 2 x \approx 227, 20

(cm), így

r = \frac{d}{2} \approx 113, 60

(cm).
A félbevágott csonkakúp alakú palást felszíne:

\begin{matrix} A = \frac{(r + R) \cdot a \cdot π}{2} \approx 44 064, 5 ({cm}^{2}), \end{matrix}

így a szükséges anyagmennyiség: 4,6 m

^{2}

6. Egy

8 \times 8

-as sakktábla mezőire

1

-től

64

-ig beírtuk a természetes számokat a 6.1. ábra szerint. Ezután készítettünk egy olyan alakzatot, amely

5

darab, a sakktábla mezőivel egybevágó négyzetből áll (6.2. ábra). Az így elkészített alakzatot véletlenszerűen ráhelyezzük a sakktáblára úgy, hogy annak mind az öt négyzete lefedjen egy-egy mezőt a táblán.

6.1. ábra 6.2. ábra

a)

Mennyi annak a valószínűsége, hogy a lefedett számok összege osztható

3

-mal? (6 pont)
Egy másik alkalommal a sakktábla mezőire

64

pozitív egész számot írtunk. Közülük az egyik egyjegyű, a többi kétjegyű szám. Tudjuk, hogy a felírt számok mediánja és egyetlen módusza a

68

, ami kétszer szerepel a táblán. Tudjuk továbbá, hogy a számok átlaga

67, 5

, a terjedelmük pedig

93

b)

Mely számok szerepelnek a táblán? (10 pont)

Megoldás.

a)

I. megoldás. A ,,kereszt'' összesen

6 \cdot 6 = 36

-féleképpen helyezhető rá a sakktáblára (összes eset száma). Ha a bal felső sarokba rakjuk a keresztet, akkor a 2; 9; 10; 11 és 18 számokat fedi le, melyek összege 50, aminek a hármas maradéka 2.
Bárhová is rakjuk le a keresztet (a szabálynak megfelelően), ha eggyel jobbra csúsztatjuk az összeg mindig 5-tel, a hármas maradék pedig 2-vel nő. Ha a keresztet eggyel lefelé csúsztatjuk, akkor az összeg mindig 40-nel, a hármas maradék pedig 1-gyel nő. Az előbbiek miatt a maradékok alapján összesen 12 olyan elhelyezés van, amikor a lefedett számok összege osztható 3-mal (kedvező esetek száma).
Így a keresett valószínűség:

\frac{12}{36} = \frac{1}{3}

.
II. megoldás. A ,,kereszt'' alakzatot csak a belső négyzetekre tudjuk ráhelyezni. Ezt

6 \cdot 6 = 36

-féleképpen tudjuk megtenni (összes eset száma).
Ha a lefedett számok közül a középsőt

x

-szel jelöljük, akkor a tőle balra lévőt

x - 1

, jobbra lévőt

x + 1

, felette lévőt

x - 8

, alatta lévőt

x + 8

jelöli. Ezek összege

5 x

. Az összeg pontosan akkor osztható 3-mal, ha

x

osztható 3-mal. A

6 \times 6

-os belső négyzetben 12 db 3-mal osztható szám van (kedvező esetek száma).
Így a keresett valószínűség:

\frac{12}{36} = \frac{1}{3}

b)

Mivel 69; 70; 71;

...

; 99 összesen 31 darab szám, és a módusz valamint a medián is 68, a 64 számot sorbarendezve a két középső

x_{32} = x_{33} = 68

. A terjedelem miatt

x_{1} = 6

. A 64 szám átlaga 67,5, ezért a táblára írt számok összege 4320.
A második 32 szám összege

\frac{68 + 99}{2} \cdot 32 = 2672

. Így

\begin{matrix} s = 6 + x_{2} + x_{3} + ... + x_{31} + 68 = 4320 - 2672 = 1648, \end{matrix}

vagyis

x_{2} + x_{3} + ... + x_{31} = 1574

.
A legnagyobb összeg, ami az

x_{2}

;

x_{3}

;

...

;

x_{31}

helyén álló számokkal elérhető lenne:

38 + 39 + ... + 67 = 1575

. Ez csak 1-gyel több a valóságos összegnél, tehát valamelyik számot 1-gyel csökkenteni kell. Ez a szám csak a 38 lehet, különben két módusza lenne az táblára írt számoknak.
A keresett számok tehát: 6; 37; 39; 40;

...

; 67; 68; 68; 69; 70;

...

; 98; 99.

7. Adott a derékszögű koordináta-rendszerben az

A (11; - 2)

és a

B (2; 1)

pontokat összekötő szakasz, továbbá az

{(x + 4)}^{2} + {(y - 3)}^{2} = 20

egyenletű kör. Az

A B

szakaszt a koordináta-rendszer origója körül

+ 90^{\circ}

-kal elforgatjuk.

a)

Számítással igazoljuk, hogy a forgatással kapott szakasz egy pontban metszi a megadott kört. (4 pont)
Egy

r

és

R

sugarú kör kívülről érinti egymást. A körök középpontjain áthaladó egyenes ezeket a köröket az érintési ponton kívül az

A

és

B

pontokban metszi. Az egyik közös külső érintő érintési pontjai

E

és

F

b)

Igazoljuk, hogy az

A B E F

négyszög húrnégyszög. (6 pont)

c)

Számítsuk ki a közös külső érintőszakasz hosszát. (6 pont)

Megoldás.

a)

I. megoldás. Az

A

pont elforgatottjának koordinátái

A' (2; 11)

, a

B

ponté pedig

B' (- 1; 2)

. Mivel

36 + 64 = 100 > 20

, ezért

A'

a kör külső pontja. Mivel

9 + 1 = 10 < 20

, ezért

B'

a kör belső pontja.
Tehát az

A' B'

szakasz egy pontban metszi a megadott kört.
II. megoldás. Az

A

pont elforgatottjának koordinátái

A' (2; 11)

, a

B

ponté pedig

B' (- 1; 2)

, ezért az elforgatott pontokon átmenő egyenes egyenlete

y = 3 x + 5

. Az előbbi egyenes metszéspontjai a megadott körrel

P (0; 5)

és

Q (- 2; - 1)

.
A metszéspont akkor van az elforgatott szakaszon, ha a pontok koordinátáira teljesül, hogy

- 1 < x < 2

és

2 < y < 11

, ami csak a

P

pontra igaz, így az

A' B'

szakasz valóban egy pontban metszi a megadott kört.

b)

A B E F

négyszög akkor húrnégyszög, ha a szemközti szögeinek összege

180^{\circ}

. Az ábra jelöléseit használva legyen az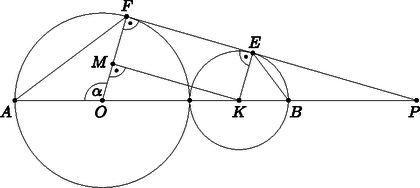

A O F ∢ = α

, ekkor

O A F ∢ = O F A ∢ = 90^{\circ} - \frac{α}{2}

Hasonló meggondolással megmutatható, hogy

K B E ∢ = B E K ∢ = \frac{α}{2}

, így az

A B E F

négyszög

A

B

E

és

F

csúcsánál lévő belső szögek rendre

90^{\circ} - \frac{α}{2}

\frac{α}{2}

90^{\circ} + \frac{α}{2}

és

180^{\circ} - \frac{α}{2}

. A szemközti szögek összege tehát

180^{\circ}

, így a négyszög valóban húrnégyszög.

c)

K

pontból párhuzamost húzva az

E F

közös érintővel a megrajzolt szakasz és

O F

metszéspontja legyen

M

. Ekkor az

O M K

derékszögű háromszögben

\begin{matrix} M K^{2} = E F^{2} = {(R + r)}^{2} - {(R - r)}^{2}, \end{matrix}

ahonnan

E F = 2 \sqrt[]{R r}

8. Egy szabadulószobának három bejárata van. Egy

6

fős társaság tagjai bármelyik ajtón, de csak kettesével léphetnek be. A belépés sorrendje nem számít.

a)

Hányféle módon juthatnak be a szobába a társaság tagjai? (4 pont)
A szabadulószoba egyik feladata így szólt: adott tíz látszólag egyforma lakat illetve tíz kulcs. Mindegyik lakatra igaz, hogy pontosan egy kulcs nyitja. A játékszabály szerint a játékosnak mind a

10

lakatot ki kell nyitnia. Nevezzük próbálkozásnak egy kulcs és egy lakat összeillesztését, akár nyitja a kulcs a lakatot, akár nem.

b)

Módszeresen dolgozva legfeljebb hány próbálkozás kell a feladat megoldásához? (3 pont)
Egy ,,túlélő'' műsorban az egyik feladat az volt, hogy a lehető leggyorsabban jussanak el a versenyzők a tengerparton lévő

A

pontból a tengeren lévő

B

pontba, mert akkor védettséget szereznek a következő megmérettetésre. Tudjuk, hogy a parton csak futhatnak, a tengerben csak úszhatnak, segédeszközöket (farönk,

evező stb.) nem használhatnak. Az ábra szerint a pálya méretei:

A Q = 4 km

B Q = 1 km

, valamint

A Q B ∢ = 90^{\circ}

. (A partvonalat az egyszerűség kedvéért tekintsük egyenesnek.) Az egyik versenyző 8 km/óra sebességgel képes futni a homokban és 2 km/óra sebességgel úszni a tengerben.

c)

Hány km futás után ugorjon a versenyző a tengerbe, ha a lehető legrövidebb időn belül szeretne eljutni

A

-ból

B

-be? (9 pont)

Megoldás.

a)

A 6 fős társaság tagjai közül a három pár

(\binom{6}{2}) \cdot (\binom{4}{2}) \cdot (\binom{2}{2}) (= 90)

-féleképpen választható ki úgy, hogy azok sorrendje is figyelembe van véve. Mivel egy adott 3 pár ebben éppen

3! (= 6)

-szor szerepel, így összesen

90 : 6 = 15

-féleképpen választható ki a 3 pár. Ezek bármelyike a 3 ajtón

3^{3} = 27

-féleképpen mehet be, tehát a keresett sorrendek száma

15 \cdot 27 = 405

b)

Az első lakat kulcsa legfeljebb 9 próbálkozással, a másodiké legfeljebb 8, a harmadiké legfeljebb 7, és így tovább, a kilencedik lakaté 1 próbálkozás után megtalálható. A tizediknél már nem kell próbálkozni, mert a megmaradt kulcs ahhoz tartozik. Tehát legfeljebb

\begin{matrix} 9 + 8 + 7 + 6 + ... + 2 + 1 = 45 \end{matrix}

próbálkozással megoldható a feladat.

c)

I. megoldás. Jelölje

U

azt a pontot, ahol a versenyzőnek a vízbe kell vetnie magát (8.1. ábra). Ekkor az

U Q = x

jelöléssel a

B U Q

derékszögű háromszögben a Pitagorasz-tétel alapján:

B U = \sqrt[]{x^{2} + 1}

. Az út megtételéhez szükséges idő:

\begin{matrix} t (x) = \frac{4 - x}{8} + \frac{\sqrt[]{x^{2} + 1}}{2}, ahol 0 \leq x \leq 4. \end{matrix}

t (x)

függvénynek ott lehet szélsőértéke, ahol

t' (x) = 0

\begin{matrix} t' (x) = - \frac{1}{8} + \frac{1}{2} \cdot \frac{1}{2} \cdot {(x^{2} + 1)}^{- \frac{1}{2}} \cdot 2 x, ebből \frac{x}{2 \sqrt[]{x^{2} + 1}} = \frac{1}{8}, \end{matrix}

ahonnan

60 x^{2} - 4 = 0

, melynek gyökei

x_{1} \approx 0, 258

és

x_{2} \approx - 0, 258

(m). (

x_{2} \approx - 0, 258

nem lehetséges,

x_{1} \approx 0, 258

megfelel.) Az

x_{1}

helyen a

t'

függvény negatívból pozitívba megy át, ezért itt

t

-nek minimuma van.
Tehát a versenyzőnek kb. 3,742 km-t kell futnia, mielőtt a tengerbe veti magát.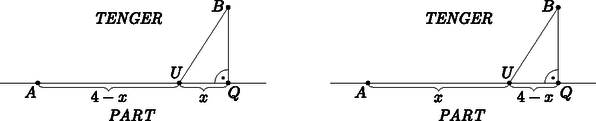

8.1. ábra 8.2. ábra

II. megoldás. Jelölje

U

azt a pontot, ahol a versenyzőnek a vízbe kell vetnie magát (8.2. ábra). Ekkor az

U Q = 4 - x

jelöléssel a

B U Q

derékszögű háromszögben a Pitagorasz-tétel alapján:

\begin{matrix} B U = \sqrt[]{x^{2} - 8 x + 17} . \end{matrix}

Az út megtételéhez szükséges idő:

\begin{matrix} t (x) = \frac{x}{8} + \frac{\sqrt[]{x^{2} - 8 x + 17}}{2}, ahol 0 \leq x \leq 4. \end{matrix}

t (x)

függvénynek ott lehet szélsőértéke, ahol

t' (x) = 0

\begin{matrix} t' (x) = \frac{1}{8} + \frac{1}{2} \cdot \frac{1}{2} \cdot {(x^{2} - 8 x + 17)}^{- \frac{1}{2}} \cdot (2 x - 8), ebből \\ \frac{\sqrt[]{x^{2} - 8 x + 17} + 4 x - 16}{8 \sqrt[]{x^{2} - 8 x + 17}} = 0, \end{matrix}

ahonnan

15 x^{2} - 120 x + 239 = 0

, melynek gyökei

x_{1} \approx 4, 258

és

x_{2} \approx 3, 742

(m). (

x_{1} \approx 4, 258

nem lehetséges,

x_{2} \approx 3, 742

megfelel.) Az

x_{2} \approx 3, 742

helyen a

t'

függvény negatívból pozitívba megy át, ezért itt

t

-nek minimuma van.
Tehát a versenyzőnek kb. 3,742 km-t kell futnia, mielőtt a tengerbe veti magát.

9. Egy öttagú család (apa, anya és a három gyerek) életkorának összege ebben az évben

100

év. Az anya

6

évvel fiatalabb a férjénél.

6

év múlva a középső gyerek kétszerannyi idős lesz, mint most. Amikor a legkisebb gyerek született, abban az évben (a kicsi megszületése előtt) a négytagú család átlagéletkora 22,5 év volt. Az anya az első gyermekét

22

éves korában szülte.

a)

Hány éves most az anyuka? (7 pont)
Vasárnap délután a családtagok egy új társasjátékot próbálnak ki. A társasjáték játéktábláján

100

mező kapcsolódik egymás után, melyeket a tervezők

1

-től

100

-ig megszámoztak. A táblán a második mezőtől kezdve minden

2.

mező zöld színű (a többi fehér), a harmadik mezőtől kezdve minden

3.

mezőn egy állat képe, a negyedik mezőtől kezdve minden

4.

mezőn egy fa képe, és az ötödik mezőtől kezdve minden

5.

mezőn egy vadászház képe látható. A játékszabály szerint, ha egy mezőn két figura szerepel, akkor az erre a mezőre lépő játékos egyszer kimarad a játékból.

b)

Hány olyan fehér színű mező van a táblán, amelyre lépve a játékos egyszer kimarad a játékból? (3 pont)
A társasjáték játékszabálya szerint a játékosok egy fehér és egy sárga színű szabályos dobókockával dobnak egyszerre, és a lépésük száma a dobott számok összege. Ha a dobás összege

6,

akkor a játékosok újra dobhatnak, és a lépések száma a játékos által dobott négy szám összege lesz. (Például: Ha a játékos első dobása

2

és

5

volt, akkor a

7

-es mezőre lép. Ha viszont a játékos első dobása

2

és

4

, az új dobása

3

és

5

volt, akkor a játékos a

14

-es mezőre léphet.) Ha egy mező sorszáma

10

-zel osztható, akkor erre rálépve, a játékos a bábujával visszalép a legközelebbi, fát ábrázoló mezőre.

c)

Mennyi annak a valószínűsége, hogy az első játékos bábuja kezdéskor a

10

-es mezőre lép? (Kezdéskor a játékosok bábui az

1

-es mező előtt állnak.) (6 pont)

Megoldás.

a)

Jelölje az apa életkorát most

x

, a középső gyerekét

y

. Ekkor a szöveg alapján az anya

x - 6

, a középső gyerek pedig az

y + 6 = 2 y

egyenletből 6 éves.
A legkisebb gyerek születésének évében a két nagyobb gyerek és a két szülő életkorának összege

22, 5 \cdot 4 = 90

év. A legkisebb gyerek születése óta az öttagú család életkorának összege 10 évvel nőtt, tehát a legkisebb gyerek most 2 éves.
Ha az anya most

x - 6

éves, akkor a legidősebb gyerek

x - 6 - 22 = x - 28

éves. Mivel az életkorok összege 100 év, ezért

2 + 6 + (x - 28) + x + (x - 6) = 100

, ahonnan

x = 42

, így az anyuka 36 éves.

b)

1-től 100-ig a 3 és az 5 páratlan közös többszöröseit keressük. Mivel

[3; 5] = 15

, így a 15., 45. és 75. mező ilyen, azaz a keresett mezők száma 3.

c)

A játékos csak úgy léphet a 10-es mezőre, ha az első két dobás összege 10, vagy az első két dobás összege 6 és az utána következő két dobás összege 4.
Az első két dobás összege úgy lehet 10, ha a játékos a

(4; 6)

(6; 4)

, vagy

(5; 5)

párosítások valamelyikét dobja. Ennek a valószínűsége

\frac{3}{36}

.
Az első két dobás összege úgy lehet 6, ha a játékos az

(1; 5)

(5; 1)

(2; 4)

(4; 2)

vagy

(3; 3)

párosítások valamelyikét dobja. Ennek a valószínűsége

\frac{5}{36}

.
Az első két dobást követő dobás összege úgy lehet 4, ha a játékos az

(1; 3)

(3; 1)

vagy

(2; 2)

párosítások valamelyikét dobja. Ennek a valószínűsége

\frac{3}{36}

.
(A két egymás utáni dobás egymástól független esemény), így ennek a valószínűsége

\frac{5}{36} \cdot \frac{3}{36}

. A keresett valószínűség:

\begin{matrix} \frac{3}{36} + \frac{5}{36} \cdot \frac{3}{36} = \frac{41}{432} \approx 0, 095. \end{matrix}