Kezdőlap


Cím:	Konvex poliéderek egyensúlyi pontjai
Szerző(k):	Domokos Gábor , Kovács Flórián , Lángi Zsolt , Regős Krisztina , Varga Péter Tamás
Füzet:	2020/május, 264 - 273. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Bevezetés

Jelen folyóirat egy korábbi számában megjelent cikkben [5] vízszintes síkra helyezett, saját tömeggel rendelkező konvex poliéderek stabil egyensúlyi helyzeteire vonatkozó eredményeket ismerhettünk meg. Ezen cikkben, az egyensúlyi pont fogalmának ismertetése után, többek között két állítás bizonyítását olvashatjuk:

$•$	Minden homogén tömegeloszlású (röviden: homogén) tetraédernek legalább két stabil egyensúlyi pontja van (azaz van két olyan lapja, melyen a test elbillenés nélkül megáll), illetve

$•$	létezik olyan homogén $19$ lapú konvex poliéder, melynek pontosan egy stabil egyensúlyi pontja van.

Érdemes megjegyezni, hogy az első állítás megtalálható, mint a Gnädig Péter, Honyek Gyula és Vígh Máté szerkesztette, 333 furfangos feladat fizikából című feladatgyűjtemény F. 120-as feladata [4]. Az említett [5] cikk végén a szerző négy kérdést fogalmaz meg konvex poliéderek egyensúlyi pontjaira vonatkozóan. Ezek közül az első három kérdés stabil egyensúlyi pontokra vonatkozik, és a cikkben megtalálhatjuk a felvetett problémákkal kapcsolatos ismereteink összefoglalását is. Jelen írásunkban többek között azzal a (negyedikként közölt) kérdéssel kívánunk részletesen foglalkozni, amely csúcsán ‐ tehát nem stabil módon ‐ egyensúlyozott tetraéderre vonatkozik:

1. kérdés. Igaz-e, hogy minden homogén tetraédernek van legalább két olyan csúcsa, amely egyensúlyi pont?

Ez a megfogalmazás a hivatkozott cikk első kérdésének ,,duálisaként'' is felfogható. A kérdés logikáját követve természetes módon adódnak a cikk végén feltüntetett kérdések csúcsokra vonatkozó változatai is, mint például a következő:

2. kérdés. Létezik-e olyan homogén poliéder, melynek összes csúcsa közül pontosan egy olyan van, amely egyensúlyi pont? Ha igen, mennyi az ilyen tulajdonságú homogén konvex poliéderek minimális csúcsszáma?

A kérdést továbbgondolva egy általánosabb kérdéshez is eljuthatunk:

3. kérdés. Adott számú és jellegű egyensúlyi ponttal rendelkező homogén poliéderek közt mennyi a minimális lap-, illetve csúcsszámú poliéder lapjainak, illetve csúcsainak száma?

Cikkünk fő témája a 3. kérdés precízebb megfogalmazása, illetve a vele kapcsolatos ismereteink összefoglalása. Ehhez viszont definiálnunk kell a konvex poliéderek egyensúlyi pontjainak különböző típusait, illetve a konvex poliéderek ezekkel kapcsolatos osztályozási rendszerét. Első lépésben talán nem árt felidéznünk egy konvex test egyensúlyi pontjának fogalmát [5].

1. definíció. Legyen

K

egy konvex test, és

X

a test egy belső pontja. Azt mondjuk, hogy a test egy

Y

határpontja

K

egy egyensúlyi pontja

X

-re nézve, ha az

Y

-on átmenő,

X Y

szakaszra merőleges sík nem metszi a

K

test belsejét. Ha

X

K

test tömegközéppontja (homogén sűrűséget feltételezve), azt mondjuk, hogy az

Y

pont

K

egy egyensúlyi pontja.

Érdemes meggondolni, hogy

K

minden belső pontja lehet

K

tömegközéppontja alkalmas inhomogén sűrűséget feltételezve, valamint azt, hogy ha

Y

K

test egy egyensúlyi pontja

X

-re nézve, akkor

K

-t alátámasztva

Y

-ban egy vízszintes síkkal úgy, hogy ne billenjen el,

X

pontosan

Y

felett fog elhelyezkedni. A továbbiakban nem csupán stabil egyensúlyi pontokkal foglalkozunk, így érdemes azzal folytatnunk, hogy az egyensúlyi pontok szóba jöhető típusait ‐ akár homogén, akár inhomogén sűrűségeloszlást feltételezve ‐ definiáljuk.
Képzeljük el, hogy az

Y

egyensúlyi pontban alátámasztott testet kicsit kibillentjük az egyensúlyi helyzetéből. Előfordulhat, hogy ezt bármilyen irányban megcsinálva a test visszabillen az egyensúlyi helyzet felé, vagy éppen ellenkezőleg, tovább billen, és távolodik az egyensúlyi helyzettől. Előfordulhat az is, hogy a billentés irányától függően a test időnként vissza-, időnként pedig tovább billen az egyensúlyi helyzethez képest. Ezekben az esetekben az egyensúlyi helyzetet rendre stabil, instabil, vagy nyereg típusú egyensúlyi helyzetnek hívjuk. Ezekre példa egy kocka lapközéppontja, csúcsai, illetve élközéppontjai. A precíz matematikai megfogalmazáshoz az alábbi definíciót adjuk.

2. definíció. Legyen

P

egy konvex poliéder,

X

P

tömegközéppontja és

Y

P

egyensúlyi pontja

X

-re nézve.

$•$	Ha $Y$ a $P$ egy lapjának belső pontja, akkor azt mondjuk, hogy $Y$ egy stabil egyensúlyi pont.

$•$	Ha $Y$ a $P$ egy élének belső pontja, és az $X Y$ szakaszra merőleges, $Y$ -on átmenő sík $P$ -t csak ebben az élben metszi, azt mondjuk, hogy $Y$ egy nyereg típusú egyensúlyi pont.

$•$	Ha $Y$ a $P$ egy csúcsa, és az $X Y$ szakaszra merőleges, $Y$ -on átmenő sík $P$ -t csak ebben a csúcsban metszi, azt mondjuk, hogy $Y$ egy instabil egyensúlyi pont.

$•$	Ha $Y$ -ra a fenti három feltétel egyike sem teljesül, azt mondjuk, hogy $Y$ egy degenerált egyensúly.

Meggondolható, hogy

P

határának a súlyponthoz legközelebbi pontja mindig stabil, a legtávolabbi pontja pedig mindig instabil egyensúlyi pont, tehát

P

-nek mindig van legalább egy stabil, és legalább egy instabil pontja.
A matematikai analízis egyik híres tételéből, a Poincaré‐Hopf-tételből [1] következik, hogy ha egy konvex poliédernek csak nemdegenerált egyensúlyi pontjai vannak, akkor a stabil pontok

S

, instabil pontok

U

és a nyeregpontok

H

száma kielégíti az

\begin{matrix} S - H + U = 2 \end{matrix}

összefüggést. Érdemes ezt összehasonlítani a jól ismert Euler-tétellel, mely szerint ha egy konvex poliédernek

f

lapja,

e

éle és

v

csúcsa van, akkor

f - e + v = 2

. Ezen mennyiségek jól szemléltethetők az 1. ábrán látható három poliéder segítségével.

1. ábra. Három homogén sűrűségű poliéder és jellemző számadataik: a lapok (

f

), csúcsok (

v

) és élek (

e

) száma, a stabil (

S

), instabil (

U

) és nyereg-típusú (

H

) egyensúlyi pontok száma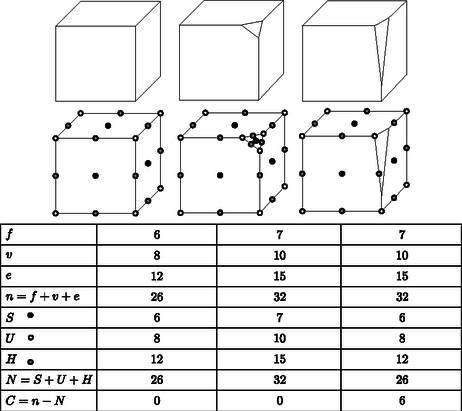, ezek összege (

n = f + v + e

N = S + U + H

), valamint a poliéderek mechanikai komplexitása (

C = n - N

, lásd a 3. definíciót).

A cikk további részében csak olyan konvex poliéderekkel foglalkozunk, melyeknek nincsenek degenerált egyensúlyi pontjai.

2. Poliéderek komplexitása

Ahogy a bevezetőben említettük, ,,nemdegenerált'' esetben, azaz ha a poliéder minden egyensúlyi pontja stabil, instabil, vagy nyeregpont, akkor ezek

S

U

és

H

száma kielégíti az

S - H + U = 2

összefüggést. Így a fenti adatok közül pl.

S

és

U

értéke meghatározza

H

értékét is. A továbbiakban

{(S, U)}^{E}

-vel fogjuk jelölni az

S

stabil és

U

instabil egyensúlyi ponttal rendelkező konvex poliéderek családját. Hasonlóan, az Euler-tétel szerint minden konvex poliéder

f

lapszáma,

e

élszáma és

v

csúcsszáma kielégíti az

f - e + v = 2

összefüggést. Ennek alapján az

f

lapú és

v

csúcsú konvex poliéderek családját

{(f, v)}^{K}

-val fogjuk jelölni. Ezen osztályokat rendre a poliéder egyensúlyi, illetve kombinatorikus osztályának nevezzük.
Említettük, hogy tetszőleges konvex poliédernek van legalább egy stabil és legalább egy instabil pontja, azaz tetszőleges

{(S, U)}^{E}

osztályban

S, U \geq 1

. Hasonlóan, minden konvex poliédernek van legalább

4

lapja és csúcsa, azaz minden

{(f, v)}^{K}

osztályban

f, v \geq 4

. Erről az osztályozási rendszerről többet is tudunk. Steinitz egy tétele [6] szerint pontosan akkor van

f

lapú és

v

csúcsú konvex poliéder, ha

\begin{matrix} f \geq 4, és \frac{f}{2} \leq v \leq 2 f - 4. \end{matrix}

(1)

A továbbiakban azokat a pozitív egészekből álló

(f, v)

számpárokat, melyek az (1) egyenlőtlenségeket kielégítik, poliedrikus számpároknak nevezzük.

A cikkünkben tárgyalt fő fogalom az alábbi.

3. definíció. Legyen

P

egy konvex poliéder, melynek nincs degenerált egyensúlyi pontja. Jelölje

N (P)

a poliéder összes egyensúlyi pontjának számát, és

n (P)

a lapjai, élei és csúcsai számának összegét. Ekkor a

C (P) = n (P) - N (P)

mennyiséget a

P

poliéder (mechanikai) komplexitásának nevezzük.

Vegyük észre, hogy a poliéder minden lapja, csúcsa és éle legfeljebb egy egyensúlyi pontot tartalmaz. Tehát ha

P \in {(f, v)}^{K}

és

P \in {(S, U)}^{E}

, akkor

S \leq f

és

U \leq v

, amiből a

H \leq e

is következik a nyeregpontok

H

és az élek

e

számára. Így

P

komplexitása nem lehet negatív. Másképp megfogalmazva,

P

komplexitása azon lapjainak, éleinek és csúcsainak száma, melyek nem tartalmaznak egyensúlyi pontot, azaz pl. egy szabályos poliéder komplexitása nulla. A komplexitás értéke jól szemléltethető az illető poliéder

(f, v)

és

(S, U)

síkokon elfoglalt helyével, pontosabban ezen helyek egymáshoz viszonyított átlós távolságával, amint azt a 2. ábrán is láthatjuk.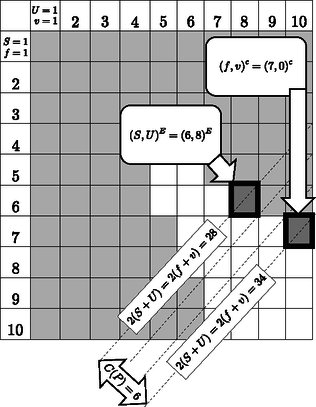

2. ábra. Az 1. ábra jobb szélén látható poliéder elhelyezkedése az

(S, U)

és

(f, v)

síkokon. A komplexitás értéke a megfelelő cellákon átmenő feltüntetett átlók távolságával arányos.

4. definíció. Legyen

S, U \geq 1

. Az

{(S, U)}^{E}

egyensúlyi osztály (mechanikai) komplexitásán az osztályhoz tartozó poliéderek komplexitásának minimumát értjük. Másképpen:

\begin{matrix} C (S, U) = {min}_{}^{} {C (P) : P \in {(S, U)}^{E}} . \end{matrix}

P \in {(f, v)}^{K}

és

P \in {(S, U)}^{E}

, akkor a Poincaré‐Hopf-tétel és az Euler-tétel alapján

C (P) = 2 (f + v - S - U)

. Minthogy

f \geq S

és

v \geq U

, az

\begin{matrix} R (S, U) = {min}_{}^{} {f + v - S - U : f \geq S, v \geq U és (f, v) egy poliedrikus pár} \end{matrix}

mennyiség kétszerese alsó becslése a

C (S, U)

komplexitásnak.

1. megjegyzés. Minden

S, U \geq 1

esetén

C (S, U) \geq 2 R (S, U)

S

és

U

mennyiségek értékeitől függően explicit módon is megadhatjuk

R (S, U)

értékét, ahol az

⌈ x ⌉

mennyiség az

x

valós szám értéke felfelé kerekítve egészekre.

\begin{matrix} R (S, U) = {\begin{matrix} ⌈ \frac{S}{2} ⌉ - U + 2, & ha S > 4 és S > 2 U - 4, \\ ⌈ \frac{U}{2} ⌉ - S + 2, & ha U > 4 és U > 2 S - 4, \\ 8 - S - U, & ha S, U \leq 4, \\ 0 & egyébként. \end{matrix} \end{matrix}

(2)

Ezen képletek geometriai jelentése a 3. ábrán látható. Mivel minden poliédernek legalább

4

lapja és

4

csúcsa van, ha

S, U \leq 4

, akkor

C (S, U)

legalább akkora, mint az

(S, U)

osztály ,,távolsága'' a

(4,4)

osztálytól, azaz ,,optimális esetben'' az osztály egy tetraédert tartalmaz, ez a magyarázata a 3. esetben szereplő képletnek. Ha

(S, U)

egy poliedrikus pár, akkor ,,optimális esetben''

{(S, U)}^{E}

tartalmaz egy

S

lapú és

U

csúcsú poliédert. Ez felel meg az

R (S, U) = 0

esetnek. Ha

(S, U)

nem poliedrikus pár, mert pl.

S

nagy

U

-hoz képest, azaz

S > 4

és

S > 2 U - 4

, akkor a legtöbb, amit remélhetünk, hogy találunk az osztályban egy poliédert, melynek

S

lapja van, és a legkevesebb csúcsa, ami egy

S

lapú poliédernek lehet, azaz

⌈ \frac{S}{2} ⌉ + 2

. Ebből vezethető le az 1. esetben, illetve analóg módon a 2. esetben szereplő képlet.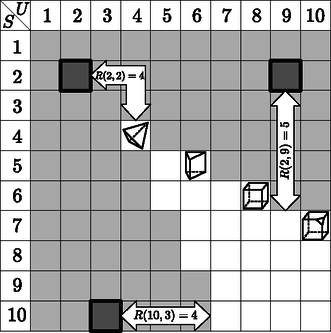

3. ábra. Az

R (S, U)

függvény értelmezése

S, U \leq 10

esetén (az

(S, U)

táblázatot néhány poliéder képe illusztrálja, a poliedrikus párokhoz tartozó cellák világos hátterűek). Adott

(S, U)

párhoz tartozó

R (S, U)

érték kiolvasható a táblázatból az

(S, U)

mezőnek a legközelebbi fehér mezőtől mért diszkrét távolságaként, lásd a sötétszürke hátterű (

{(2,2)}^{E}, {(2,9)}^{E}, {(10,3)}^{E}

egyensúlyi osztályoknak megfelelő) három példát.

Felmerülhet a kérdés, hogy milyen

{(S, U)}^{E}

osztályokra teljesülhet a

C (S, U) = 2 R (S, U)

egyenlőség. Ahogy az [5] cikkben láttuk, az

{(1, U)}^{E}

1 \leq U \leq 4

osztályok nem tartalmaznak tetraédert, tehát ezekben az osztályokban biztosan nem igaz az egyenlőség. Az alábbi állítás, melyet Domokos és szerzőtársai [2] igazoltak 2018-ban azt mutatja, hogy az említett egyenlőség az

{(S,1)}^{E}

1 \leq S \leq 4

osztályokban sem teljesül.

1. tétel. Nincs homogén sűrűségű mono-instabil tetraéder, azaz minden tetraédernek legalább két csúcsa instabil egyensúlyi pont.

3. Az egyensúlyi osztályok komplexitási korlátai

A fentiek alapján talán meglepő, hogy az alábbi tétel [2] igaz.

2. tétel. Ha

S, U \geq 2

, akkor

C (S, U) = 2 R (S, U)

.
Ezen tétel egyik speciális eseteként azt kapjuk, hogy ha van

S

lapú és

U

csúcsú poliéder, akkor van

S

lapú és

U

csúcsú olyan poliéder is, melynek minden lapján és csúcsában van egyensúlyi pont.
A tétel bizonyítása azzal egyenértékű, hogy minden

{(S, U)}^{E}

osztályban konstruálunk egy konvex poliédert, melynek komplexitása éppen

2 R (S, U)

. Ezt több lépésben tehetjük meg. A

2 \leq S, U \leq 5

egyenlőtlenségek teljesülése esetén az

{(S, U)}^{E}

osztályban számítógép segítségével kereshető alkalmas poliéder: tetraéder, ha

S, U \leq 4

, és négyszög alapú gúla, ha

S = 5

vagy

U = 5

. Az

{(S, S)}^{E}

S \geq 6

osztályokban közvetlenül, geometriai megfontolások alapján található ezen osztálybeli,

S

lapú és

S

csúcsú poliéder:

S \geq 4

esetén egy szabályos

(S - 1)

-szög alaplapú egyenes gúla éppen a megkívánt tulajdonságú. Végül a többi osztályban megfelelő tulajdonságú poliéder a fenti poliéderek apró deformációival kapható meg.

1. táblázat. Egy-egy példa az

{(S, U)}^{E}

S, U \in {2,3,4}

(S, U) \neq 4,4

egyensúlyi osztályokba tartozó tetraéderekre. A tetraéderek alábbi hat koordinátája adott konstans:

A_{x} = A_{y} = A_{z} = B_{y} = C_{z} = 0

B_{x} = 1

4. ábra. Az

{(S, U)}^{E}

S, U \in {2,3,4,5}

egyensúlyi osztályokhoz tartozó (az 1‐2. táblázatokban szereplő) 8 tetraéder, illetve 6 pentaéder, valamint a szabályos tetraéder és a szimmetrikus négyzet alapú gúla 3D nyomtatással készült példányai.

\begin{matrix} osztály & nemkonstans csúcsponti koordináták \\ C_{x} & C_{y} & D_{x} & D_{y} & E_{x} & E_{y} & E_{z} \\ (2,5) & 1,0 & 1,7 & 0,5 & - 0, 3 & 2,1 & 1,2 & 1,2 \\ (3,5) & 1,0 & 1,7 & 3,8 & - 2, 2 & 1,6 & 0,9 & 0,9 \\ (4,5) & 2,5 & 1,4 & 3,8 & - 2, 2 & 2,0 & 1,2 & 1,2 \\ (5,2) & 1,0 & 1,7 & 0,9 & 0,5 & - 0, 6 & - 1, 1 & - 1, 1 \\ (5,3) & 1,0 & 1,7 & 0,9 & 0,5 & 1,5 & 2,6 & 2,6 \\ (5,4) & 1,0 & 1,7 & 1,3 & 0,8 & 1,5 & 2,6 & 2,6 \end{matrix}

2. táblázat. Egy-egy példa az

(i,5)

és

(5, i)

i \in {2,3,4}

egyensúlyi osztályokba tartozó pentaéderekre. A pentaéderek alábbi hét koordinátája adott konstans:

A_{x} = A_{y} = A_{z} = B_{x} = C_{z} = D_{z} = 0

B_{y} = 1

Mi a helyzet az

{(S,1)}^{E}

és az

{(1, S)}^{E}

osztályokkal? A

C (S, U) \geq 2 R (S, U)

egyenlőtlenség egy alsó becslést ad

C (S, U)

értékére. Adható felső becslés is? A válasz a legtöbb osztályra megtalálható a már említett [2] cikkben.

3. tétel. Ha

S \geq 4

akkor

C (S,1) \leq 59 + {(- 1)}^{S} + 2 R (S,1)

; ha

U \geq 4

akkor

C (1, U) \leq 90 + 2 R (1, U)

.
Talán érdemes megjegyezni, hogy az ezen tételben szereplő második, azaz a monostabil poliéderekre vonatkozó egyenlőtlenség igazolásához szükséges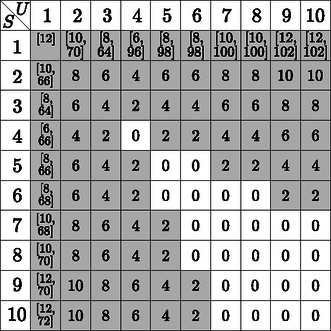

{(1, U)}^{E}

-osztályú konvex poliéderek a Conway és Guy által konstruált, a [5] cikkben ismertetett monostabil (az

{(1,4)}^{E}

osztályba tartozó) poliéder apró deformációival állíthatók elő. A már hivatkozott [2] cikkben szereplő módszerek alkalmazásával konstruálható poliéder a

{(2,1)}^{E}

5. ábra. Az egyensúlyi osztályok mechanikai komplexitása: az eredmények összefoglalása

S, U \leq 10

esetén (a poliedrikus pároknak megfelelő cellák itt is világos hátterűek). A zárójel nélkül szereplő egész számok pontos komplexitási értéket, az

S = 1

sorban és

U = 1

oszlopban szögletes zárójelbe tett számok komplexitási korlátokat jelentenek (két érték alsó és felső korlátot, egyetlen érték pedig csupán alsó korlátot ad meg ‐ itt a felső korlát ismeretlen).

{(3,1)}^{E}

{(1,2)}^{E}

és az

{(1,3)}^{E}

osztályokban is, melyek mindegyike egy-egy felső korlátot ad az osztály komplexitásának mértékére, sőt az

{(S,1)}^{E}, S > 3

egyensúlyi osztályok komplexitásának felső korlátját ugyancsak e

{(2,1)}^{E}

és

{(3,1)}^{E}

osztályba tartozó két test apró deformációival konstruált testek segítségével kaphatjuk meg. A

{(2,1)}^{E}

és

{(3,1)}^{E}

egyensúlyi osztályokhoz konstruált poliéder olyan test, amelynek 18 csúcsa van, így tehát a 2. kérdés második felére jelenleg a következő válasz adható: mivel mono-instabil homogén sűrűségű tetraéder nem létezik, a homogén sűrűségű mono-instabil testek minimális csúcsszáma legfeljebb 18, de legalább 5. Az 5. ábra táblázata összefoglalja az egyensúlyi osztályok komplexitásával kapcsolatos legjobb ismert becsléseket.
Az 5. ábra alapján az egyetlen osztály, melyről nem tudjuk, hogy tartalmaz-e konvex poliédert, az

{(1,1)}^{E}

osztály. Érdemes megjegyezni, hogy általában a konvex testek közt ismert egy olyan homogén test, melynek egy stabil és egy instabil egyensúlyi pontja van. Ez a test, mely a fentiek szerint rendelkezik azzal a tulajdonsággal, hogy (eltekintve az instabil egyensúlyi pontjától), bármilyen helyzetben alátámasztva addig gördül, amíg megtalálja egyetlen stabil egyensúlyi helyzetét, Gömböc néven ismert, és a 6. ábrán látható.

6. ábra

Felvetődhet az ötlet, hogy egy Gömböcöt poliéderrel nagyon finoman közelítve kaphatunk egy

{(1,1)}^{E}

osztályú konvex poliédert. Sajnos, intuíciónkkal talán ellentétes módon megmutatható, hogy ,,egyenletes'' közelítést használva tetszőleges finomság esetén a keletkező poliédernek egynél több stabil, illetve instabil egyensúlyi pontja lesz. Ezt a jelenséget tárgyalja a [3] cikk.
Ösztönözve a kutatást a kis lap- és csúcsszámú, Gömböc-tulajdonságú homogén konvex poliéderek keresésére, a cikket egy nemrég kitűzött díjra való felhívással fejezzük be. Ezen,

C (1,1)

értékének meghatározásáért kitűzött díj értéke amerikai dollárban:

\begin{matrix} \frac{10^{6}}{C (1,1)} . \end{matrix}

A díj elnyerésének részletesebb feltételeit az érdeklődő olvasó megtalálhatja a [2] cikkben. Aki a díjjal kapcsolatban ennél bővebb információt szeretne vagy érdeklődne a jelen cikkben ismertetett téma felől, a cikk szerzőivel tudja felvenni a kapcsolatot.

Hivatkozások

[1]	V.I. Arnold, Ordinary differential equations 10th printing, 1998. MIT Press.

[2]	G. Domokos, F. Kovács, Z. Lángi, K. Regős and P.T. Varga, Balancing polyhedra, arXiv:1810.05382 [math.MG], October 12, 2018.

[3]	G. Domokos, Z. Lángi and T. Szabó, On the equilibria on finely discretized curves and surfaces, Monatsh. Math., 168 (2012), 321‐345.

[4]	Gnädig Péter, Honyek Gyula és Vígh Máté, 333 furfangos feladat fizikából, Typotex Kiadó, Budapest, 2014.

[5]	Lángi Zs. Konvex poliéderek stabil lapjai, Középiskolai Matematikai és Fizikai Lapok, 69(5) (2019), 258‐264.

[6]	E. Steinitz,Über die Eulersche Polyderrelationen, Arch. Math. Phys., 11 (1906), 86‐88.

Domokos Gábor
domokos@iit.bme.hu
Lángi Zsolt
zlangi@math.bme.hu
Kovács Flórián
kovacs.florian@epito.bme.hu
Regős Krisztina
regoskriszti@gmail.com
Varga Péter Tamás
petercobbler@gmail.com