Kezdőlap


Cím:	Térbe kilépő bizonyítások, ráadás
Szerző(k):	Kós Géza
Füzet:	2020/május, 258 - 264. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Gergonne megoldása az Apollóniusz-feladatra

Ebben a cikksorozatban olyan bizonyításokat mutatunk be, amikor a geometriai alakzatokat ,,térbe kilépve'', három- vagy akár még magasabb dimenziós objektumok vetületeként vagy metszeteként állítjuk elő.¹

A pergai Apollóniusztól² származtatják a következő klasszikus feladatot.
Apollóniusz-feladat: Adott három kör,

k_{1}

k_{2}

és

k_{3}

. Szerkesszük meg az összes olyan

m

kört, amely

k_{1}

k_{2}

és

k_{3}

mindegyikét érinti.
A feladatnak sokféle speciális és elfajuló esete létezik: valamelyik kör helyett egyenes (végtelen sugarú kör) is lehet, illetve a kör egy ponttá fajulhat (nulla sugarú kör), ilyenkor az érintés helyett azt követeljük meg, hogy

m

átmenjen az illető ponton. Néhány nagyon speciális esettel már általános iskolában találkoztunk, mint például három adott ponton átmenő, vagy a három adott egyenest érintő körök megszerkesztése.
Szeretjük kikötni, hogy

k_{1}

k_{2}

és

k_{3}

általános helyzetű legyen, vagyis a középpontjaik ne essenek egy egyenesre, ne menjenek át egy ponton, ne érintsék egymást, a sugaraik különbözőek legyenek, és a három körnek ne legyen közös érintője. Ismert, hogy általános helyzetű körök esetén az

m

kör nyolc- vagy négyféle lehet, és az is elfordulhat, hogy nincs ilyen érintő kör; egy-egy ilyen elrendezést lerajzoltam az 1a.‐1c. ábrákon.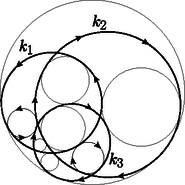

1a. ábra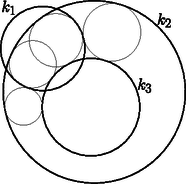

1b. ábra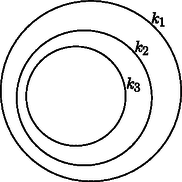

1c. ábra

A megoldásokat (az érintő köröket) csoportokba rendezhetjük úgy, hogy a köröket és egyeneseket irányítjuk, és csak olyan érintést engedünk meg, amikor az egymást érintő köröknek és egyeneseknek az iránya is megegyezik. Az 1.a ábrán a nyilacskák jelzik az egyik lehetséges irányítást; a nyolc érintő kör közül kettő felel meg ennek a szigorúbb feltételnek. Világos, hogy csak annak van jelentősége, hogy

k_{1}

k_{2}

k_{3}

közül mely párok azonos vagy ellentétes irányításúak, tehát a megoldásokat négy (esetleg üres) csoportba osztottuk. Érdemes a feladatot így is megfogalmazni:
Irányított Apollóniusz-feladat: Adott három irányított kör,

k_{1}

k_{2}

és

k_{3}

. Szerkesszük meg az összes olyan

m

irányított kört, amely

k_{1}

k_{2}

és

k_{3}

mindegyikét érinti úgy, hogy az érintési pontokban a körök iránya azonos.
Az Apollóniusz-feladatra sokféle megoldás ismert; talán a legszebb Gergonne³ szerkesztése. A cikksorozatnak ebben az utolsó utáni részében az ő szerkesztését szeretném bemutatni.

Az azonos sugarú körök esete

k_{1}

k_{2}

és

k_{3}

irányítása azonos (mondjuk pozitív), és a sugaruk ugyanakkora, akkor könnyű dolgunk van. Legyen a három kör középpontja

K_{1}

K_{2}

, illetve

K_{3}

, a közös sugár

r

. Rajzoljuk meg a

K_{1}

K_{2}

K_{3}

pontokon átmenő

c

kört; ennek középpontja legyen

O

, sugara

r_{0}

. (Előfordulhat, hogy

r_{0} < r

.) Könnyű meggondolni, hogy a feladatnak két megoldása van, az

O

középpontú,

| r_{0} - r |

sugarú

m_{1}

kör és az

r_{0} + r

sugarú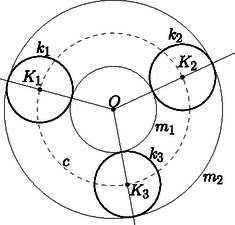

m_{2}

kör (2. ábra).

2. ábra

Az általános esetet megpróbálhatjuk visszavezetni az egyenlő sugarú esetre, ehhez hasznos és kézenfekvő eszköz az inverzió: kereshetünk egy olyan inverziót, vagy inverziók egymás utánját, amely előbb két, majd végül mindhárom kört ugyanakkora sugarú, és azonos irányítású körbe képezi. Helyette inkább egy másik irányt szeretnék mutatni, amely nem fog minden esetben működni, de jól bemutatja a Gergonne-féle szerkesztést, és hogy milyen matematikai érdekességek vannak mögötte.

Azonos sugarú körök a félsíkmodellben

A cikksorozat 6. részében már láttunk példákat arra, hogy a Poincaré-féle félsíkmodellben különböző méretűnek látszó körvonalak mégis lehetnek ,,ugyanakkorák'': két körvonal akkor ,,ugyanakkora'', ha a külső hasonlósági pontjuk a félsíkmodell határára esik. Nosza, szerkesszük meg az irányított

k_{1}

k_{2}

és

k_{3}

köreink párjainak hasonlósági pontjait; legyen

k_{i}

és

k_{j}

hasonlósági pontja

H_{i j}

. A Monge-tételből tudjuk, hogy a három hasonlósági pont egy

h

egyenesre esik; ha szerencsénk van, akkor a

h

-nak ugyanazon az oldalán van

k_{1}

k_{2}

és

k_{3}

; ezt a félsíkot fogjuk a félsíkmodellnek tekinteni. A

k_{i}

kör ,,középpontja'' a modellben legyen

K_{i}

, és legyen

r

a közös ,,sugár''. Rajzoljuk meg ismét a

K_{1}

K_{2}

K_{3}

pontokon átmenő

c

körvonalat; ismét csak ha szerencsénk van, akkor

c

teljes egészében a félsík belsejébe esik, vagyis egy hiperbolikus ,,kör''. Legyen

c

modellbeli ,,középpontja'' az

O

pont. A feladat két megoldását, az

m_{1}

és

m_{2}

köröket úgy kapjuk, hogy ugyanezzel a középponttal rajzolunk egy

r

-rel kisebb, és egy

r

-rel nagyobb sugarú kört (3. ábra).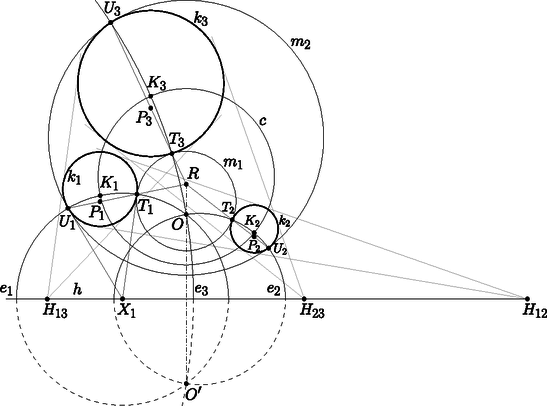

3. ábra

Azt gondolhatnánk, hogy ezzel vége, megszerkesztettük a két érintő kört, de inkább tanulmányozzuk tovább az ábrát; a lényeg csak ezután következik. Jelöljük

T_{i}

-vel, illetve

U_{i}

-vel a

k_{i}

érintési pontját az

m_{1}

, illetve az

m_{2}

körrel. A

T_{i}

pont a

k_{i}

és az

m_{1}

külső hasonlósági pontja, az

U_{i}

pedig

k_{i}

és

m_{2}

külső hasonlósági pontja; a Monge-tétel miatt a

T_{i} U_{i}

egyenes átmegy

m_{1}

és

m_{2}

belső hasonlósági pontján; jelöljük ezt

R

-rel.
Rajzoljuk meg az

O

és

K_{i}

pontokat összekötő

e_{i}

,,egyeneseket'' is, amelyek a határra merőleges félkörnek látszanak. (Ezzel már kilenc kört zsúfoltunk össze az ábrán.) A félkörök meghosszabbításai átmennek az

O

pont

h

-ra vonatkozó tükörképén, az

O'

ponton. A

c

m_{1}

m_{2}

körök közös ,,középpontja'' az

O

pont, ezért a látszólagos középpontjaik az

O O'

egyenesre esnek, így az

R

pont is az

O O'

egyenesen van.
Az első fontos észrevételünk, hogy az

R

pontnak a

k_{1}

k_{2}

k_{3}

és

e_{1}

e_{2}

e_{3}

körökre vonatkozó hatványa ugyanaz: az

R O O'

egyenes az

e_{1}

e_{2}

e_{3}

körök közös hatványvonala,

k_{i}

és

e_{i}

hatványvonala pedig az

R T_{i} U_{i}

egyenes. Tehát: az

R

pont a

k_{1}

k_{2}

k_{3}

körök hatványpontja.
Legyen most

X_{i}

e_{i}

félkör középpontja. Az

e_{i}

félkör átmegy

k_{i}

,,középpontján'', ezért merőleges

k_{i}

-re; emiatt az

X_{i} T_{i}

és

X_{i} U_{i}

szakaszok a

k_{i}

érintői. A

k_{i}

körben a

T_{i} U_{i}

egyenes az

X_{i}

pont polárisa; mivel

X_{i}

h

egyenesen van, az

R T_{i} U_{i}

egyenes átmegy a

h

egyenes

k_{i}

-re vonatkozó pólusán (az ábrán

P_{i}

-vel jelöltem).

Gergonne szerkesztése az Apollóniusz-feladatra

Az előbbi okoskodásból elhagyhatjuk a félsíkmodellt, a

c

és az

e_{i}

köröket, és leolvashatjuk Gergonne módszerét.
Gergonne szerkesztése: Legyen

k_{1}

k_{2}

és

k_{3}

hatványpontja

R

, jelölje

k_{i}

és

k_{j}

hasonlósági pontját

H_{i j}

. A három hasonlósági pont egyenese legyen

h

, és a

k_{i}

körben legyen

h

pólusa a

P_{i}

pont. Az irányított Apollóniusz-feladatnak akkor létezik megoldása, mégpedig pontosan kettő, ha mindegyik

k_{i}

kört elmetszi a megfelelő

R P_{i}

egyenes, és a két metszéspont éppen a

k_{i}

két érintési pontja a két megoldás körrel.
Egy igazán jó szerkesztési eljárástól elvárjuk, hogy az összes megoldást megtalálja, és lehetőleg ne produkáljon hamis megoldásokat, amelyeket tovább kell válogatnunk. A fenti szerkesztésben van egy kis bizonytalanság: a módszer mindegyik

k_{i}

körön megadja a két megoldás érintési pontjait, de azt még el kell döntenünk, hogy mely érintési pontok tartoznak ugyanahhoz a körhöz.

Gergonne eljárása megszerkeszti a megoldásokat

Előbb azt fogjuk ellenőrizni, hogy ha az irányított Apollóniusz-feladatnak létezik megoldása, akkor Gergonne módszere megszerkeszti ezt a megoldást, mégpedig két különböző kört, és a két megoldás érintési pontjainak megkülönböztetésére is mutatunk egy egyszerű módszert.
Tegyük fel, hogy valamilyen

m_{1}

irányított kör megoldása az irányított Apollóniusz-feladatnak;

m_{1}

és

k_{i}

érintési pontját jelölje

T_{i}

.
Először megszerkesztjük a másik megoldást. Legyen az

R

hatványpontnak a

k_{1}

k_{2}

k_{3}

körökre vonatkozó közös hatványa

λ

. Az

R

középpontú,

λ

paraméterű inverzió⁴ a

k_{1}

k_{2}

k_{3}

köröket önmagukra képezi;

λ > 0

esetén az irányításukat megfordítja. Jelöljük

T_{i}

inverzét

U_{i}

-vel, és

m_{1}

inverzét

m_{2}

-vel; ha

λ > 0

, akkor

m_{2}

legyen

m_{1}

-gyel ellentétes irányítású. Az inverzió érintéstartósága miatt az

m_{2}

kör érinti mindegyik

k_{i}

kört az

U_{i}

pontban, és az irányításuk is megegyezik. Tehát

m_{2}

egy másik megoldása a feladatnak.
Az

m_{1}

k_{i}

és

k_{j}

irányított körök páronként vett hasonlósági pontjai

T_{i}

T_{j}

és

H_{i j}

; ezek a Monge-tétel szerint egy egyenesen vannak; ugyanígy, az

m_{2}

k_{i}

és

k_{j}

körök páronként vett hasonlósági pontjai, az

U_{i}

U_{j}

és

H_{i j}

is egy egyenesen vannak (4. ábra).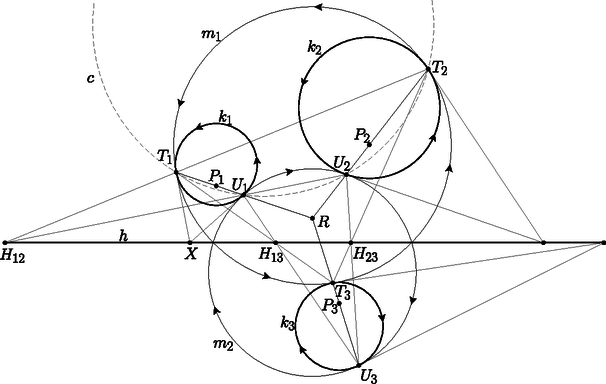

4. ábra

m_{2}

szerkesztése miatt

R T_{1} \cdot R U_{1} = R T_{2} \cdot R U_{2} = λ

, ezért

T_{1}

T_{2}

U_{1}

U_{2}

egy

c

körön van. A

c

és

m_{1}

hatványvonala a

T_{1} T_{2}

egyenes, a

c

és

m_{2}

hatványvonala az

U_{1} U_{2}

egyenes. A két hatványvonal metszéspontja a

H_{12}

pont, tehát

H_{12}

hatványa az

m_{1}

és

m_{2}

körökre ugyanakkora. Ugyanez igaz a

H_{13}

és a

H_{23}

pontokra is; ebből látjuk, hogy a

h

egyenes az

m_{1}

és az

m_{2}

hatványvonala.
Most húzzuk meg

k_{1}

közös érintőit az

m_{1}

és

m_{2}

egyenesekkel; ezek metszéspontja legyen

X

. A

T_{1} X

egyenes a

k_{1}

és

m_{1}

hatványvonala, az

U_{1} X

egyenes pedig a

k_{1}

és

m_{2}

hatványvonala, tehát

X

rajta van az

m_{1}

és

m_{2}

hatványvonalán is, ami ‐ mint láttuk ‐ a

h

. Másrészt a

T_{1} U_{1}

egyenes az

X

pont polárisa a

k_{1}

körben; mivel

h

átmegy az

X

ponton, az

X

polárisa is átmegy a

h

pólusán, a

P_{1}

ponton. Tehát a

P_{1}

pont az

R T_{1} U_{1}

egyenesen van. Ugyanígy láthatjuk, hogy az

R T_{2} U_{2}

és az

R T_{3} U_{3}

egyenes is átmegy

P_{2}

-n, illetve

P_{3}

-on.
Ezzel ellenőriztük, hogy Gergonne módszere tényleg megszerkeszti a megoldásokat. Az is látszik, hogy a hat érintési pontot hogyan kell két hármas csoportba osztanunk: ha már eldöntöttük, hogy mondjuk a

k_{1}

kör és az

R P_{1}

egyenes két metszéspontja közül melyik a

T_{1}

és melyik az

U_{1}

, akkor a további négy metszéspont közül

T_{j}

az, amelyik a

H_{1 j} T_{1}

egyenesen,

U_{j}

pedig az, amelyik a

H_{1 j} U_{1}

egyenesen van (

j = 2,3)

.
Ha számítógéppel szeretnénk ábrát rajzolni a szerkesztéshez, akkor

T_{1}

és

U_{1}

kijelölése után a

T_{j}

és az

U_{j}

pontot az

R P_{j}

egyenes és a

H_{1 j} T_{1}

, illetve

R P_{j}

és

H_{1 j} U_{1}

metszéspontjaként érdemes definiálnunk.

Gergonne eljárása csak a megoldásokat szerkeszti meg

A megfordítás is igaz: amit Gergonne módszere megszerkeszt, azok valóban megoldások.
A

k_{1}

kör és az

R P_{1}

egyenes két metszéspontját betűzzük meg

T_{1}

-gyel és

U_{1}

-gyel. A két megoldást úgy fogjuk megszerkeszteni, hogy a

k_{1}

kört a

T_{1}

, illetve az

U_{1}

pontból felnagyítjuk. A

T_{2}

U_{2}

T_{3}

U_{3}

pontokat máshogy fogjuk definiálni, de végül ugyanazok a pontok lesznek.
Legyen a

k_{1}

kör második metszéspontja a

H_{12} T_{1}

és a

H_{12} U_{1}

egyenessel

A

, illetve

B

. Először megmutatjuk, hogy az

A B

egyenes átmegy a

P_{1}

ponton. Vizsgáljuk a

k_{1}

körbe írt

T_{1} U_{1} A B

négyszöget a

k_{1}

-re vonatkozó polaritás szerint. Legyen az

A U_{1}

és

B T_{1}

egyenesek metszéspontja

Y

, az

A B

és

T_{1} U_{1}

egyenesek metszéspontja pedig

Z

.
A

H_{12} Y Z

háromszög autopoláris, ezért a

Z

pont polárisa a

H_{12} Y

egyenes, és ezen rajta van a

T_{1} U_{1}

egyenes pólusa, az

X

pont is. Tehát

Z

polárisa a

h

egyenes, és

Z = P_{1}

.
A

k_{1}

kört középpontosan a

k_{2}

körbe nagyíthatjuk a

H_{12}

pontból; az

A

B

T_{1}

U_{1}

pontok képét jelöljük rendre

T_{2}

U_{2}

C

-vel, illetve

D

-vel; a

P_{1}

pont képe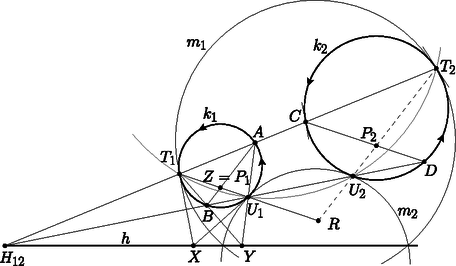

P_{2}

. Mivel

\begin{matrix} 1 = \frac{H_{12} T_{1} \cdot H_{12} A}{H_{12} U_{1} \cdot H_{12} B} = \frac{H_{12} T_{1} \cdot H_{12} T_{2}}{H_{12} U_{1} \cdot H_{12} U_{2}}, \end{matrix}

T_{1}

U_{1}

T_{2}

U_{2}

pontok egy körön vannak. A

k_{1}

k_{2}

és a

T_{1} U_{1} T_{2} U_{2}

körök hatványpontja

R

, emiatt a

T_{2} U_{2} P_{2}

egyenes átmegy

R

-en is. Tehát

T_{2}

és

U_{2}

valóban a

k_{2}

kör és az

R P_{2}

egyenes két metszéspontja (5. ábra).

5. ábra

Vegyük észre, hogy a

T_{1} P_{1} A

és

C P_{2} T_{2}

háromszögek hasonlók, mert a megfelelő oldalaik párhuzamosak; a két háromszöget ugyanaz a

H_{12}

középpontú nagyítás viszi egymásba, mint a

k_{1}

és a

k_{2}

kört; emiatt a

k_{1}

kör

T_{1}

-ben és

A

-ban húzott érintői párhuzamosak a

k_{2}

kör

C

-ben, illetve

T_{2}

-ben húzott érintőivel.
Nagyítsuk a

T_{1}

pontból a

k_{1}

kört

\frac{T_{1} R}{T_{1} P_{1}}

-szeresére; a

k_{1}

képe legyen az

m_{1}

irányított kör: az

m_{1}

kör a

T_{1}

pontban érinti

k_{1}

-et, és

T_{2}

-ben érinti

k_{2}

-t, és az irányuk is megegyezik.
Hasonlóan, nagyítsuk az

U_{1}

pontból a

k_{1}

kört

\frac{U_{1} R}{U_{1} P_{1}}

-szeresére, az így kapott kör legyen

m_{2}

. A

T_{i}

és

U_{i}

pontok felcserélésével ugyanígy kapjuk, hogy az

m_{2}

kör az

U_{1}

pontban érinti

k_{1}

-et, és

U_{2}

-ben érinti

k_{2}

-t.
Ugyanezt elmondhatjuk a

k_{2}

helyett a

k_{3}

körrel is, így definiáljuk a

T_{3}

és

U_{3}

pontokat. Mivel az

m_{1}

és

m_{2}

definíciójában csak a

k_{1}

kör és az

R

P_{1}

T_{1}

és

U_{1}

pontok szerepelnek, azt kapjuk, hogy ugyanaz az

m_{1}

és

m_{2}

kör

k_{3}

-at érinti a

T_{3}

, illetve az

U_{3}

pontban.

Feladatok

1. Szerkesszük meg azokat a köröket, amelyek átmennek két adott ponton, és érintenek egy adott egyenest.

2. Szerkesszük meg azokat a köröket, amelyek átmennek egy adott ponton, és érintenek két adott egyenest.

3. Az

A B C

háromszögbe írt kör a

B C

oldalt a

D

pontban érinti. A

B C

oldalhoz hozzáírt kör középpontját

D

-vel összekötő egyenes a beírt kört másodszor a

T

pontban metszi. Mutassuk meg, hogy a

B T C

kör érinti a beírt kört.

4. A körökre illesztett kúpokkal igazoljuk, hogy az irányított Apollóniusz-feladatnak nulla vagy két megoldása van.

Fuss el véle

Ideje ezt a hosszúra nyúlt sorozatot befejezni, a tanévnek is a végére értünk. Mindenkinek köszönöm a figyelmet és a türelmet; különösen azoknak, akik végigolvasták, és a feladatokon is gondolkodtak.

¹A cikksorozat a Rényi Intézet és a Sztaki támogatásával készült.

²Pergai Apollóniusz () görög matematikus és csillagász, Kr.e. 2‐3. század.

³Joseph Diez Gergonne francia matematikus, 1771‐1859.

⁴Pozitív $λ$ esetén a $\sqrt[]{λ}$ sugarú körre vonatkozó inverzió, negatív $λ$ esetén a $\sqrt[]{| λ |}$ sugarú körre vonatkozó inverzió tükörképe.