Kezdőlap


Cím:	Vezető henger mozgása homogén mágneses térben
Szerző(k):	Berke Martin
Füzet:	2020/május, 297 - 305. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek, Mozgó elektromos töltésre ható erő (Lorentz-erő)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Vezető henger mozgása homogén mágneses térben

Fizika feladatok megoldása során nagy szerephez jutnak bizonyos ,,trükkök'', ,,mesterfogások''. Ezen írás célja, hogy egy érdekes és tanulságos példán keresztül két hasznos eljárást is bemutasson, amelyek segítségével ‐ bizonyos esetekben ‐ fémek elektromos térben való ,,viselkedése'' leírható.

A probléma

Feladatunk, hogy leírjuk, milyen töltéselrendeződés alakul ki egy hosszú, vékony falú fémhenger felületén, ha a fémhengert homogén mágneses térbe helyezzük, majd az indukcióvonalakra merőleges irányban kis sebességgel (a fénysebességnél sokkal lassabban) mozgatjuk. Legyen a henger sugara

R

, sebességének nagysága

v_{0}

, a mágneses indukció nagysága pedig

B

.
A vezető hengerben szabad töltéshordozók vannak, melyek elmozdulhatnak, így a semleges testben megváltozhat a töltéseloszlás. Ha a feladatot az ,,álló''

K

vonatkoztatási rendszerben próbáljuk megoldani, akkor az reménytelenül bonyolulttá válik. Próbálkozzunk meg olyan

K'

rendszerben dolgozni, ami a hengerrel együtt

v_{0}

sebességgel mozog a mágneses térre és a henger tengelyére merőleges irányban (1. ábra). (Vegyük észre, hogy a

K'

rendszer is inerciarendszer, hiszen a sebessége

K

-hoz képest időben állandó.) A

K'

rendszerben a henger áll, tehát a benne lévő szabad töltéshordozókra (az elektronokra) biztosan nem hat a mágneses térből származó Lorentz-erő. A mozgó rendszerbe való áttéréssel látszólag kiküszöböltük a henger mozgásából fakadó nehézséget, azonban ‐ mint látni fogjuk ‐ ennek az áttérésnek ,,ára'' van.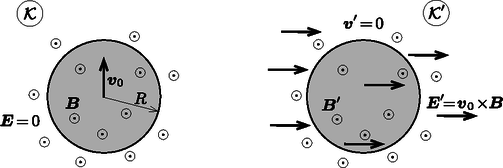

1. ábra. Homogén mágneses térben mozgó fémhenger

Az egyszerűség kedvéért a henger helyett vizsgáljunk csak egyetlen ponttöltést, amely homogén mágneses és elektromos mezőben mozog! Legyen a pontszerű test sebességvektora

v

, a töltése

Q

, a mágneses indukció vektora

B

, az elektromos térerősségvektor pedig

E

. A ponttöltésre ható erő az álló rendszerben:

\begin{matrix} F = Q (v \times B) + Q E . \end{matrix}

Üljünk most egy

v_{0}

sebességgel mozgó vonatkoztatási rendszerbe, és írjuk fel a részecskére ható erőt ebben a (vesszősen jelölt) rendszerben is:

\begin{matrix} F' = Q ({v-v}_{0}) \times B' + Q E' . \end{matrix}

Hasonlítsuk össze a két rendszerben felírt erőt! Mivel mindkét vonatkoztatási rendszer inerciarendszer, nyilván teljesül, hogy

F = F'

(hiszen a töltött részecske gyorsulása ugyanakkora mindkét inerciarendszerben), vagyis fennáll:

\begin{matrix} v \times (B - B') + E + (v_{0} \times B') - E' \equiv 0. \end{matrix}

A részecske (tetszőleges irányú)

v

sebességével arányos tag eltűnéséből

\begin{matrix} B' = B, \end{matrix}

a sebességétől független tagokból pedig

\begin{matrix} E' = E + (v_{0} \times B) \end{matrix}

adódik.¹
A számunkra fontos esetben, amikor az álló rendszerben nincs elektromos tér, vagyis

E \equiv 0

, a mozgó rendszerben tapasztalható homogén elektromos mező térerősségvektora:

\begin{matrix} E' = v_{0} \times B . \end{matrix}

Visszatérve az eredeti problémához a feladatunk nem más, mint meghatározni, milyen töltéselrendeződés alakul ki egy homogén fémhenger felületén, ha a tengelyére merőleges, homogén elektromos térbe helyezzük, melynek nagysága

\begin{matrix} E_{0} = v_{0} B . \end{matrix}

(1)

A következőkben két különböző módszerrel is megoldjuk ezt a feladatot. Az egyik matematikailag könnyebb, ám egy szokatlan gondolatot (,,mesterfogást'') igényel. A másik eljárás a tükörtöltés módszerét alkalmazza; ez talán hamarabb eszünkbe juthat, azonban a számolás hosszadalmasabb.

A szuperpozíció módszere

Az első megoldás során egy olyan trükkel élünk, amely ugyan elég speciális, azonban hasznos lehet hasonló jellegű elektrosztatikai feladatok megoldásánál. A fémek belsejében egyensúlyi állapotban nem lehet elektromos tér, így olyan töltéselrendezést keresünk, amelyet az eredeti, külső térre szuperponálva a henger belsejében zérus elektromos teret eredményez.
Vizsgáljuk meg, hogy milyen az elektromos tere egy egyenletes térfogati töltéssűrűséggel rendelkező, hosszú hengernek a henger belsejében. Ehhez a Gauss-féle fluxustörvényt fogjuk felírni a henger egy

h

hosszúságú darabjára. Az elrendezés forgásszimmetrikus, a térerősség erővonalai sugárirányúak, a térerősségvektor nagyságát meghatározó összefüggés pedig

\begin{matrix} \frac{ϱ h r^{2} π}{ε_{0}} = 2 r π h E (r) . \end{matrix}

A fenti összefüggésben

ϱ

a henger térfogati töltéssűrűségét,

r

pedig a henger tengelyétől mért távolságot jelöli. Mivel most csak az

r < R

esetet vizsgáljuk, ennek megfelelően írtuk fel a Gauss-törvényt. Rendezve az egyenletet az elektromos térerősség nagyságára ezt kapjuk:

\begin{matrix} E (r) = \frac{r ϱ}{2 ε_{0}} . \end{matrix}

Vizsgáljunk most két hengert, az egyik (a

P

középpontú) henger pozitív, a másik (a

Q

középpontú) pedig negatív térfogati töltéssűrűséggel rendelkezik (2. ábra). Tekintsünk egy tetszőleges

A

pontot a mindkét henger által lefedett részen! A

\vec{P Q}

\vec{P A}

és

\vec{Q A}

vektorok segítségével, illetve az elektromos térerősségvektor nagyságára kapott összefüggés felhasználásával az

A

pontban az elektromos térerősség a következő alakban írható fel: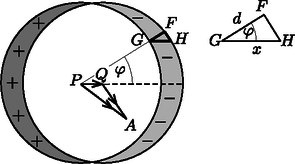

2. ábra. Ellentétesen töltött hengerek

\begin{matrix} E_{A} = \frac{ϱ}{2 ε_{0}} \vec{P A} - \frac{ϱ}{2 ε_{0}} \vec{Q A} = \frac{ϱ}{2 ε_{0}} \vec{P Q} . \end{matrix}

(2)

Látjuk, hogy a két henger átfedő részén az elektromos térerősség vektora nem függ az

A

pont helyzetétől, tehát valóban homogén elektromos mező alakul ki. Mi a helyzet azon részekkel, ahol nincs a hengerek között átfedés? A

P Q

, valamint

P G

szakaszok által bezárt szöget jelöljük

φ

-vel. Ha a

P Q

távolság

x

, akkor a

G F

szakasz hossza

\begin{matrix} d = x cos φ . \end{matrix}

(3)

(Kihasználtuk, hogy a

G H

szakasz hossza éppen

x

, és a két henger tengelye kellően közel van egymáshoz, emiatt az

F H

körív egy rövid, egyenes szakasszal közelíthető.)
Tekintsünk egy keskeny,

Δ A

területű sávot a henger felületén! A töltés ebben a részben a következő alakban írható fel:

\begin{matrix} η Δ A = d ϱ Δ A, \end{matrix}

(4)

ahol

ϱ

az egységnyi térfogatban lévő töltés nagysága,

η

pedig az egységnyi felület töltése (felületi töltéssűrűség). Mivel a külső tér nagysága (1) szerint

v_{0} B

, így

E_{A} = v_{0} B

, hiszen ekkor lesz zérus elektromos tér a fémen belül. A (2)‐(3)‐(4) egyenletek alapján a felületi töltéssűrűség már könnyen kiszámítható:

\begin{matrix} η = 2 ε_{0} v_{0} B cos φ . \end{matrix}

(5)

A két, ellentétesen töltött henger segítségével létrehozott elektromos tér a külső elektromos térrel együtt éppen olyan eredő teret ad, amely a fémhengeren belül eltűnik. A kapott eredmény szerint a felületi töltéssűrűség függ a henger felületén megválasztott pont helyétől. A második megoldás során azt is látni fogjuk, hogy a szögfüggés milyen fizikai tartalommal bír.

Tükörtöltések 2 dimenzióban

A második megoldás során a tükörtöltés módszerét fogjuk alkalmazni. Ez a módszer kiválóan alkalmazható ,,magasfokú'' szimmetriával rendelkező töltéselrendeződések estén, bizonyos esetekben azonban a számítások hosszadalmassá válhatnak. Az alábbiakban ismertetésre kerülő módszer alkalmas lehet még elektromosan feltöltött szálak és fémhengerek közötti erőhatás, illetve párhuzamos fémhengerek kapacitásának meghatározására is.
A tükörtöltés módszer alkalmazása speciális geometriai viszonyokat kíván. Jól ismert, hogy egy fémsík (fémsíkok) vagy egy fémgömb közelében elhelyezkedő pontszerű töltés és a fém együttes elektromos tere olyan lesz, mintha a valódi töltésen kívül egy alkalmas helyen elhelyezkedő és alkalmas nagyságú másik töltés (tükörtöltés) is jelen lenne. (Ez az erőtér csak a fémfelület egyik oldalán, a valódi töltést tartalmazó térrészben érvényes, a másik oldalon az elektromos térerősség nulla.)
Esetünkben nem ilyen egyszerű a helyzet. A hosszú henger eltolási szimmetriájából kiindulva megsejthetjük, hogy hosszú, egyenletesen feltöltött szigetelő szálak elektromos terét érdemes vizsgálnunk. Tekintsünk két hosszú, párhuzamos, elektromosan töltött szálat, melyeken a vonalmenti töltéssűrűség (vagyis ez egységnyi hosszon található töltés)

\pm λ

. Legyen a két szál egymástól

2 d

távolságban (

d ≫ R

), a fémhenger szimmetriatengelye pedig a szálakkal párhuzamosan, azok között ,,félúton'', a szálaktól

d

távolságban helyezkedjék el.
Az elektromos tér nagyságát egy-egy szál esetén a Gauss-törvény alkalmazásával kaphatjuk meg, majd a szuperpozíció elvét alkalmazva kiszámíthatjuk az eredő teret. Egyetlen szál esetén az elektromos térerősségvektor nagysága a száltól

r

távolságban

\begin{matrix} E_{szál} (r) = \frac{λ}{2 π ε_{0}} \frac{1}{r}, \end{matrix}

iránya pedig a szálra merőleges (tehát sugárirányú) lesz. Mivel a

λ

és

- λ

töltéssűrűségű szálak a hengertől messze találhatók, így a henger ,,helyén'' jó közelítéssel homogén elektromos tér alakul ki, amelynek nagysága:

\begin{matrix} E_{0} = \frac{λ}{π ε_{0}} \frac{1}{d} . \end{matrix}

(6)

A tükörtöltések (pontosabban fogalmazva: a tükörszálak) helyét úgy kell megválasztani, hogy a fémhenger felülete ekvipotenciális legyen. (Ilyenkor az elektromos térerősségvektor a felület bármely pontjában merőleges a felület érintősíkjára, ún. normális irányú.) Helyezzünk el ‐ gondolatban ‐ a henger szimmetriatengelyétől

x

távolságban, a két távoli töltött szál által meghatározott síkban egy

μ

, az ,,átellenes'' helyen pedig

- μ

vonalmenti töltéssűrűséggel ellátott szálat (3. ábra).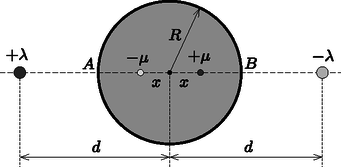

3. ábra. Töltéselrendezés a tükörtöltéses módszer alkalmazásánál

Megjegyzés. A tükörtöltések nagyságát azért választottuk

λ

-tól (elvben) függetlennek, mert egy fémgömb esetében a tükörtöltés módszere akkor működik, ha különböző helyekre különböző nagyságú töltéseket helyezünk el. Később látni fogjuk, hogy a fémhenger csak a

μ = λ

választás lesz eredményes.

A szálak közül válasszuk ki például a

λ

és

- μ

vonalmenti töltéssűrűségű párt, majd vizsgáljuk meg ezek eredő potenciálfüggvényét. Ennek a függvénynek az állandóságát szeretnénk elérni a fémhenger felülete mentén. (A másik két szálat azért hagyjuk figyelmen kívül, mert az elrendezés szimmetrikus. Ha az említett két szál tere ekvipotenciális a hengerfelületen, akkor a másik két szál tere is az lesz, tehát a négy szál eredő potenciálja is állandó nagyságú a felületen.)
A potenciálfüggvény felírásához először tekintsünk egyetlen egy szálat, amelynek vonalmenti töltéssűrűsége

λ^{*}

, és vizsgáljuk meg, hogy mekkora munkavégzéssel tudunk egy

q

nagyságú próbatöltést az önkényesen kiválasztott

r_{0}

távolságú pontból sugárirányban mozgatva a száltól

r

távolságra lévő pontba juttatni. A mozgatáshoz szükséges erő a száltól

r'

távolságban

\begin{matrix} F (r') = - q E (r') = - \frac{q λ^{*}}{2 π ε_{0}} \frac{1}{r'} . \end{matrix}

Ez az erő változó nagyságú, ezért a teljes munkavégzést, ami

q U (r

)-rel egyenlő, a kicsiny elmozdulásokon végzett munkák összegzésével (integrálásával) számíthatjuk ki:

\begin{matrix} q U (r) & = \sum Δ W = \sum F (r') Δ r' = - \frac{q λ^{*}}{2 π ε_{0}} \sum_{r' = r_{0}}^{r} \frac{Δ r'}{r'} \approx - \frac{q λ^{*}}{2 π ε_{0}} \int_{r_{0}}^{r} \frac{d r'}{r'} = \\ = - \frac{q λ^{*}}{2 π ε_{0}} (ln r - ln r_{0}) . \end{matrix}

Megállapíthatjuk tehát, hogy egyetlen töltött szál elektromos potenciálfüggvénye:

\begin{matrix} U (r) = - \frac{λ^{*}}{2 π ε_{0}} ln r + állandó . \end{matrix}

(Az állandó értéke a potenciál nullpontjának, vagyis

r_{0}

-nak megválasztásától függ. Ezt a nullpontot ‐ a ponttöltés háromdimenziós esetétől eltérően ‐ nem tehetjük a ,,végtelen'' távoli pontba, de nyilván nem választhatjuk a szál helyét sem kiindulási pontnak.)
Visszatérve az eredeti elrendezéshez azt kapjuk, hogy a

λ^{*} = + λ

vonalmenti töltéssűrűséggel ellátott száltól

r_{1}

, a

λ^{*} = - μ

vonalmenti töltéssűrűséggel ellátott száltól pedig

r_{2}

távolságra lévő pontban a potenciál értéke:

\begin{matrix} U = \frac{λ}{2 π ε_{0}} ln (r_{1}) - \frac{μ}{2 π ε_{0}} ln (r_{2}) + állandó . \end{matrix}

Mivel a henger felülete ekvipotenciális, teljesülnie kell az

\begin{matrix} \frac{{(r_{1})}^{λ}}{{(r_{2})}^{μ}} = állandó \end{matrix}

(7)

feltételnek. Már az ókor óta ismert az a geometriai tétel, miszerint a sík azon pontjai, amelyek két adott ponttól mért távolságainak aránya állandó, egy körön (az ún. Apollóniosz-körön) helyezkednek el. Eszerint a (7) egyenlet csak akkor határoz meg a síkban egy kört (a térben pedig hengerfelületet), ha

λ = μ

, mert ilyen esetben

r_{1} / r_{2} = állandó.

Hátravan még az

x

távolság meghatározása. Tekintsük ismét a korábban kiválasztott két szál potenciálját! Az

A

és a

B

pontokban a potenciál egyenlőségét felhasználva írhatjuk, hogy

\begin{matrix} U_{A} = \frac{λ}{2 π ε_{0}} ln (\frac{d - R}{R - x}) = U_{B} = \frac{λ}{2 π ε_{0}} ln (\frac{d + R}{R + x}) . \end{matrix}

A logaritmusfüggvény monotonitását kihasználva, továbbá az argumentumokat összevetve adódik, hogy

\begin{matrix} \frac{d - R}{R - x} = \frac{d + R}{R + x}, \end{matrix}

vagyis teljesül, hogy

\begin{matrix} x = \frac{R^{2}}{d} . \end{matrix}

(8)

Mivel

d

(

R

-hez viszonyítva) nagyon nagy, (6) szerint

λ

-nak is nagyon nagynak, (8) miatt pedig

x

-nek nagyon kicsinek kell lennie. Az egymáshoz nagyon közel (

2 x

távolságra) lévő, nagy, de ellentétes töltésű szálat az egymáshoz közeli, ellentétes előjelű ponttöltések mintájára (kétdimenziós) dipólusnak nevezhetjük. A szálak vonalmenti töltéssűrűségének és a távolságuknak szorzata

\begin{matrix} p = 2 x λ = 2 π ε_{0} R^{2} E_{0} = 2 π ε_{0} R^{2} v_{0} B . \end{matrix}

Ez a mennyiség, amit (kétdimenziós) dipólmomentumnak (dipólnyomatéknak,
dipólerősségnek) neveznek, még a

d \to \infty

határesetben is véges nagyságú marad.
Azt az érdekes eredményt kaptuk, hogy a homogén elektromos mezőbe helyezett, az elektromos térerősségvektorra merőleges tengelyű fémhengernek az elektromos megosztás hatására kialakuló tere a hengeren kívül olyan, mintha a fémhenger tengelye mentén egy megfelelő erősségű dipólus is jelen lenne. Az eredő elektromos tér a dipólus erőterének és a külső (homogén) erőtérnek vektori összege. Ha ezt az eredő teret meghatározzuk, abból már könnyen leolvashatjuk a fémhenger felületére kerülő töltések mennyiségét és eloszlását.
Tekintsünk egy

p

erősségű dipólt, amit egy negatív és egy pozitív töltésű szál alkot. A dipólerősséget olyan

p

vektorral adhatjuk meg, amely a negatív töltésű száltól a pozitív felé mutat, nagysága pedig

p

. Határozzuk meg az elektromos térerősségvektor nagyságát és irányát a dipólustól

r

távolságban, a

p

vektorra merőleges, illetve azzal párhuzamos irányban (4. ábra)! Ezeket az irányokat Gauss-féle főhelyzeteknek nevezik.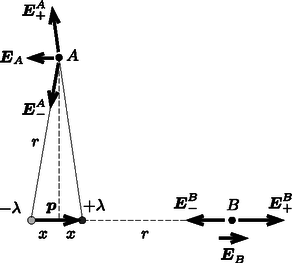

4. ábra. Dipólusszál tere a Gauss-féle főhelyzetekben

Számítsuk ki a két szál eredő térerősségét az

A

és

B

pontokban! (Kihasználjuk, hogy

2 x ≪ r

.) Mivel egyetlen szál térerőssége

\begin{matrix} E (r) = \pm \frac{λ}{2 r π ε_{0}}, \end{matrix}

az eredő tér nagysága a Gauss-féle főhelyzetekben:

\begin{matrix} E_{B} = \frac{λ}{2 r π ε_{0}} - \frac{λ}{2 (r + 2 x) π ε_{0}} \approx \frac{p}{2 π ε_{0}} \frac{1}{r^{2}}, \end{matrix}

illetve

\begin{matrix} E_{A} \approx \frac{2 λ}{2 r π ε_{0}} \frac{x}{r} = \frac{p}{2 π ε_{0}} \frac{1}{r^{2}} . \end{matrix}

Látjuk, hogy a térerősségek nagysága a főhelyzetekben ugyanakkora, de az irányuk ellentétes (lásd a 4. ábrát).
Ha nem a Gauss-féle főhelyzetekre vagyunk kiváncsiak, hanem tetszőleges pontban keressük az elektromos térerősséget, akkor az 5. ábrának megfelelően érdemes felbontani a dipólusmomentum-vektort a dipólus tengelyével

φ

szöget bezáró iránnyal párhuzamos

\begin{matrix} p_{‖} = p cos φ \end{matrix}

nagyságú, és erre az irányra merőleges

\begin{matrix} p_{⊥} = p cos φ \end{matrix}

nagyságú vektorkomponensek összegére.
Ha a ,,komponensdipólusokra'' felírjuk a Gauss-féle főhelyzeteknek megfelelő egyenleteket, akkor már könnyen kiszámíthatjuk az elektromos térerősség nagyságát a kérdéses pontban, az irányát pedig a vektorösszeadás alapján kaphatjuk meg. A dipólustól a vizsgált pontba mutató vektorral párhuzamos (ún. normális irányú) térerősséghez csak

p_{‖}

, az erre merőleges (ún. tangenciális) komponenshez pedig csak

p_{⊥}

ad járulékot.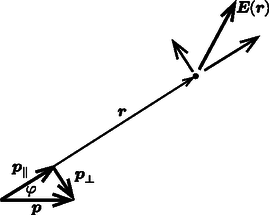

5. ábra. Dipólusszál elektromos tere tetszőleges pontban

Az eredeti problémához visszatérve tehát a henger egy adott pontjában meg kell határozni a dipólus által keltett elektromos térerősség nagyságát és irányát, majd ehhez hozzávenni a külső elektromos teret. A henger esetén az

\vec{R}

helyvektorú pontban, mely a dipólus tengelyével

φ

szöget zár be, a dipólus tere által létrehozott tangenciális és normális irányú térerősség-komponensek:

\begin{matrix} E_{t}^{dipól} = v_{0} B sin φ, E_{n}^{dipól} = v_{0} B cos φ . \end{matrix}

Ehhez vegyük hozzá a külső elektromos tér tangenciális és normális komponensét, melyek

\begin{matrix} E_{t}^{külső} = - v_{0} B sin φ, E_{n}^{külső} = v_{0} B cos φ . \end{matrix}

A külső tér tangenciális komponense ellentétes irányú a dipólus terének tangenciális komponensével. Eszerint az eredő térerősségnek valóban csak normális komponense van, melynek nagysága:

\begin{matrix} E_{n}^{eredő} = 2 v_{0} B cos φ . \end{matrix}

A fém belsejében az elektromos térerősség nulla, tehát az eredő tér normál komponensének ,,ugrása'' is

2 v_{0} B cos φ

.
A felületi töltéssűrűség a térerősség normál komponensének ugrása és

ε_{0}

szorzata. (Ezt úgy láthatjuk be, hogy ‐ gondolatban ‐ körülvesszük a felület egy kicsiny részét egy lapos, zárt ,,dobozzal'', majd alkalmazzuk erre a dobozra a Gauss-törvényt.)
Ezek szerint a felületi töltéssűrűség a

B

indukciójú mágneses térben

v

sebességgel mozgó fémcsőnél (vagy tömör fémhengernél)

\begin{matrix} η (φ) = 2 ε_{0} v_{0} B cos φ, \end{matrix}

összhangban az első módszerrel kapott (5) eredménnyel.

Megjegyzés. A mozgó fém felületén kialakuló elektromos töltéssűrűség nagysága nem függ attól, hogy egy vékony falú csövet, vagy pedig egy tömör fémrudat mozgatunk a mágneses térben. Hibás tehát az a naiv sejtés, miszerint a tömör rúdban sokkal több szabadon mozgó töltés lévén, azokból a megosztás során sokkal többet lehet a felületre ,,húzni'', mint a vékony falú cső esetében. A felületre kiülő töltések mennyiségét nem a rendelkezésre álló elektronok száma, hanem a kiegyensúlyozandó külső tér nagysága határozza meg.

A bemutatott probléma szép példája annak, amikor egy fizika feladatnak több, lényegileg különböző megoldása van, és mindegyikből sokat tanulhatunk. A bemutatott ötletek nem újdonságok, hanem kevésbé ismert ,,trükkök'', ezen írás egyik célja, hogy összefoglalja azokat.
Fontos megjegyezni, hogy habár a henger mozog, a hozzá rögzített rendszer inerciarendszer, így az elektrosztatika törvényeit a megszokott alakban írhatjuk fel. Nem ez a helyzet, ha a henger gyorsul. Érdekes, a cikkben tárgyaltakhoz hasonló gondolatokat igénylő példákat találunk a KöMaL korábban kitűzött feladatai között (lásd pl. a 3191., 3322., 3600., 4032., 4604., 4926. feladatot), illetve a 333+ Furfangos Feladat Fizikából című feladatgyűjteményben. A cikkben leírtakhoz kapcsolódó, ajánlott irodalom még: Feynman ‐ Leighton ‐ Sands: Mai fizika, V‐VI.

\begin{matrix} Berke Martin(Budapest)a BME II. éves fizika BSc szakos hallgatója \end{matrix}

¹Ezek a transzformációs képletek csak

v ≪ c

esetén érvényes, közelítőleg helyes összefüggések. A fénysebességgel összemérhető sebességű mozgásoknál (ami egy makroszkopikus testnél megvalósíthatatlan) a

B

térerősség is megváltozik.