Cím:	Megoldásvázlatok a 2020/3. szám emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Szoldatics József (Budapest)
Füzet:	2020/április, 210 - 224. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Oldjuk meg a valós számok halmazán a következő egyenletet: $\begin{array}{c}{\displaystyle x^2-14=2\sqrt[]{x^2+1}\mathrm{.}}\end{array}$ (6 pont) $b)$ Oldjuk meg a valós számok halmazán a következő egyenletrendszert: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{2x^{2}y}{2x^2+y}}& {\displaystyle =\frac{1}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{12x^{2}y}{4x^2+3y}}& {\displaystyle =\frac{1}{5}\mathrm{.}}\hfill \end{array}}$  (7 pont)     Megoldás. $a)$ A gyökjel alatti mennyiség mindig pozitív. Az egyenlet bal oldala nem lehet negatív, azaz $\begin{array}{c}{\displaystyle x^2-14\ge 0;x^2\ge 14.}\end{array}$ Vezessünk be új ismeretlent, azaz legyen $\begin{array}{c}{\displaystyle a=\sqrt[]{x^2+1}\left(\ge 0\right)\mathrm{.}}\end{array}$ Ekkor az egyenletünk az $\begin{array}{c}{\displaystyle x^2+1-15=a^2-15=2a\mathrm{,}{a}^2-2a-15=0}\end{array}$ alakot veszi fel. Ennek megoldásai $a_1=5$, $a_2=-3$. Ebből csak az $a_1$ jöhet számításba az előjel miatt, azaz $\begin{array}{c}{\displaystyle a_1=5=\sqrt[]{x^2+1}\mathrm{,}25=x^2+\mathrm{1,}{x}^2=\mathrm{24,}x=\pm \sqrt[]{24}=\pm 2\sqrt[]{6}\mathrm{.}}\end{array}$ A kapott gyököket az ellenőrzés jónak találja. $b)$ Ha $x=0$ lenne, akkor az egyenletek bal oldalán nulla állna, míg jobb oldalán nem, tehát $x\ne 0$. Ugyanezen gondolat alapján kapjuk, hogy $y\ne 0$. A megoldhatóság feltétele, hogy $2x^2+y\ne 0$ és $4x^2+3y\ne 0$ legyen. Vegyük az egyenletek reciprokait ‐ az előzőek alapján megtehetjük ‐ és rendezzük: ${\displaystyle \begin{array}{cccc}\hfill {\displaystyle \frac{2x^2+y}{2x^{2}y}}& {\displaystyle =\mathrm{2,}}\hfill & {\displaystyle \frac{4x^2+3y}{12x^{2}y}}\hfill & \hfill {\displaystyle =\mathrm{5,}}\\ \hfill {\displaystyle \frac{2x^2}{2x^{2}y}+\frac{y}{2x^{2}y}}& {\displaystyle =\mathrm{2,}}\hfill & {\displaystyle \frac{4x^2}{12x^{2}y}+\frac{3y}{12x^{2}y}}\hfill & \hfill {\displaystyle =\mathrm{5,}}\\ \hfill {\displaystyle \frac{1}{y}+\frac{1}{2x^2}}& {\displaystyle =2.}\hfill & {\displaystyle \frac{1}{3y}+\frac{1}{4x^2}}\hfill & \hfill {\displaystyle =5.}\end{array}}$ Vezessünk be új ismeretleneket: $\begin{array}{c}{\displaystyle a=\frac{1}{x^2}\mathrm{,}b=\frac{1}{y}\mathrm{.}}\end{array}$ Az egyenletrendszer az $\begin{array}{c}{\displaystyle \{{\displaystyle \begin{array}{cc}\hfill {\displaystyle {\displaystyle \frac{1}{2}}a+b}& {\displaystyle =2}\hfill \\ \hfill {\displaystyle {\displaystyle \frac{1}{4}}a+{\displaystyle \frac{1}{3}}b}& {\displaystyle =5}\hfill \end{array}}\Rightarrow \{{\displaystyle \begin{array}{cc}\hfill {\displaystyle a+2b}& {\displaystyle =4}\hfill \\ \hfill {\displaystyle 3a+4b=60}\end{array}}}\end{array}$ alakot nyeri el. Itt a második egyenletből az első kétszeresét levonva kapjuk, hogy $a=52$ és $b=-24$; azaz ${\displaystyle \begin{array}{cccc}\hfill {\displaystyle a=52}& {\displaystyle =\frac{1}{x^2}\mathrm{,}{x}^2=\frac{1}{52}\mathrm{,}}\hfill & {\displaystyle b=-24}\hfill & \hfill {\displaystyle =\frac{1}{y}\mathrm{,}y=-\frac{1}{24}\mathrm{,}}\\ \hfill {\displaystyle x}& {\displaystyle =\pm \frac{1}{\sqrt[]{52}}=\pm \frac{1}{2\sqrt[]{13}}\mathrm{.}}\hfill \end{array}}$ A kapott gyökök $(\frac{1}{2\sqrt[]{13}};-\frac{1}{24})$ és $(-\frac{1}{2\sqrt[]{13}};-\frac{1}{24})$, az ellenőrzés mindkettőt jónak találja.   2. $a)$ Oldjuk meg a valós számok halmazán a következő egyenletet: $\begin{array}{c}{\displaystyle 4^x+4\cdot 2^{-x}=5.}\end{array}$ (6 pont) $b)$ Oldjuk meg a valós számok halmazán a következő egyenletet: $\begin{array}{c}{\displaystyle \text{sin}{}^{6}x+\text{cos}{}^{6}x=-2+3\text{cos}2x\mathrm{.}}\end{array}$ (7 pont)   Megoldás. $a)$ Vezessünk be új ismeretlent, legyen $2^x=a\left(>0\right)$. Így ${\displaystyle \begin{array}{c}\hfill {\displaystyle a^2+\frac{4}{a}=\mathrm{5,}{a}^3-5a+4=\mathrm{0,}{a}^3-1-5a+5=\mathrm{0,}}\hfill \\ \hfill {\displaystyle \left(a-1\right)\left(a^2+a+1\right)-5\left(a-1\right)=\mathrm{0,}\left(a-1\right)\left(a^2+a-4\right)=0.}\hfill \end{array}}$ Egy szorzat akkor és csak akkor nulla, ha valamelyik tényezője nulla, azaz ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle a-1=\mathrm{0,}}& {\displaystyle }\hfill & {\displaystyle a^2+a-4=\mathrm{0,}}\hfill \\ \hfill {\displaystyle a_1=\mathrm{1,}}& {\displaystyle }\hfill & {\displaystyle a_2=\frac{-1+\sqrt[]{17}}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle }\hfill & {\displaystyle a_3=\frac{-1-\sqrt[]{17}}{2}\left(<0\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle 2^x=\mathrm{1,}}& {\displaystyle }\hfill & {\displaystyle 2^x=\frac{-1+\sqrt[]{17}}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle x_1=\mathrm{0,}}& {\displaystyle }\hfill & {\displaystyle x_2=\text{log}{}_2\frac{-1+\sqrt[]{17}}{2}\mathrm{.}}\hfill \end{array}}$ $a_3$ nem ad megoldást, mivel negatív. A kapott gyököket az ellenőrzés jónak találja. $b)$ Használjuk fel, hogy $\text{sin}{}^{2}x=1-\text{cos}{}^{2}x$ és $\text{cos}2x=2\text{cos}{}^{2}x-1$ igaz minden valós számra: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left(1-\text{cos}{}^{2}x\right)}^3+\text{cos}{}^{6}x}& {\displaystyle =-2+3\left(2\text{cos}{}^{2}x-1\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle 1-3\text{cos}{}^{2}x+3\text{cos}{}^{4}x-\text{cos}{}^{6}x+\text{cos}{}^{6}x}& {\displaystyle =-2+6\text{cos}{}^{2}x-\mathrm{3,}}\hfill \\ \hfill {\displaystyle 3\text{cos}{}^{4}x-9\text{cos}{}^{2}x+6}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle \text{cos}{}^{4}x-3\text{cos}{}^{2}x+2}& {\displaystyle =0.}\hfill \end{array}}$ Vezessünk be új ismeretlent, azaz $a=\text{cos}{}^{2}x$, ekkor egyenletünk az  $\begin{array}{c}{\displaystyle a^2-3a+2=0}\end{array}$ alakot veszi fel, aminek a gyökei: $a_1=2$ és $a_2=1$. Ekkor ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle a_1=2=\text{cos}{}^{2}x\mathrm{,}}& {\displaystyle }\hfill & {\displaystyle a_2=1=\text{cos}{}^{2}x\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{cos}x=\pm \sqrt[]{2}\mathrm{,}}& {\displaystyle }\hfill & {\displaystyle \text{cos}x=\pm \mathrm{1,}}\hfill \\ \hfill {\displaystyle \text{ami nem lehetséges,}}& {\displaystyle }\hfill & {\displaystyle x=k\pi ;k\in \text{Z}\mathrm{.}}\hfill \end{array}}$ A kapott gyököket az ellenőrzés jónak találja.   3. $a)$ Oldjuk meg a valós számok halmazán a következő egyenletet: $\begin{array}{c}{\displaystyle 1+\frac{3}{\text{log}{}_4\left(x^2-6x+13\right)}=\frac{4}{\text{log}{}_2\left(x+1\right)}+\frac{\text{log}{}_2{\left(x+1\right)}^2}{2}\mathrm{.}}\end{array}$ (8 pont) $b)$ Egy szabályos dobókockát hatvanszor feldobva $15$ esetben kaptunk hatost. Ezt a kísérletet egymás után többször elvégezve mindig ehhez hasonló eredményre jutunk. Emiatt úgy sejtjük, hogy a dobókocka ,,cinkelt'', azaz a hatos megnövelt valószínűséggel bír. Mekkora ez a valószínűség, ha minden $60$-as sorozat esetén $15$ lett a kapott érték $($azaz a várható érték $15)?$  (4 pont)   Megoldás. $a)$ Az egyenlet értelmezési tartományát vizsgálva: ${\displaystyle \begin{array}{cccccccc}\hfill {\displaystyle \text{log}{}_4\left(x^2-6x+13\right)}& {\displaystyle \ne \mathrm{0,}}\hfill & {\displaystyle x^2-6x+13}\hfill & \hfill {\displaystyle >\mathrm{0,}}& {\displaystyle \text{log}{}_2\left(x+1\right)}\hfill & {\displaystyle \ne \mathrm{0,}}\hfill & \hfill {\displaystyle x+1}& {\displaystyle >\mathrm{0,}}\hfill \\ \hfill {\displaystyle x^2-6x+12}& {\displaystyle \ne \mathrm{0,}}\hfill & {\displaystyle {\left(x-3\right)}^2+4}\hfill & \hfill {\displaystyle >\mathrm{0,}}& {\displaystyle x}\hfill & {\displaystyle \ne \mathrm{0,}}\hfill & \hfill {\displaystyle x}& {\displaystyle >-\mathrm{1,}}\hfill \\ \hfill {\displaystyle {\left(x-3\right)}^2+3}& {\displaystyle \ne 0.}\hfill \end{array}}$ Összefoglalva: $-1<x$ és $x\ne 0$. I. eset: $-1<x<0$. Ekkor az egyenlet jobb oldala negatív, hiszen $x<0$ esetén $\text{log}{}_2\left(x+1\right)<0$, és így ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{4}{\text{log}{}_2\left(x+1\right)}+\frac{\text{log}{}_2{\left(x+1\right)}^2}{2}}& {\displaystyle =\frac{4}{\text{log}{}_2\left(x+1\right)}+\frac{2\text{log}{}_2\left(x+1\right)}{2}=}\hfill \\ \hfill {\displaystyle =\frac{4}{\text{log}{}_2\left(x+1\right)}+\text{log}{}_2\left(x+1\right)}& {\displaystyle =\text{log}{}_2\left(x+1\right)\left(\frac{4}{\text{log}{}_2^2\left(x+1\right)}+1\right)}\hfill \end{array}}$ is negatív. A bal oldal pozitív, hiszen ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x^2-6x+13={\left(x-3\right)}^2+4}& {\displaystyle \ge \mathrm{4,}}\hfill \\ \hfill {\displaystyle \text{log}{}_4\left(x^2-6x+13\right)}& {\displaystyle \ge \text{log}{}_{4}4=\mathrm{1,}}\hfill \\ \hfill {\displaystyle 1+\frac{3}{\text{log}{}_4\left(x^2-6x+13\right)}>1.}\end{array}}$ Ebben az intervallumban tehát nincs megoldás. II. eset: $0<x$. Az egyenlet bal oldalának értékkészletét vizsgálva: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x^2-6x+13={\left(x-3\right)}^2+4}& {\displaystyle \ge \mathrm{4,}}\hfill \\ \hfill {\displaystyle \text{log}{}_4\left(x^2-6x+13\right)}& {\displaystyle \ge \mathrm{1,}}\hfill \\ \hfill {\displaystyle \frac{1}{\text{log}{}_4\left(x^2-6x+13\right)}}& {\displaystyle \le \mathrm{1,}}\hfill \\ \hfill {\displaystyle 1+\frac{3}{\text{log}{}_4\left(x^2-6x+13\right)}}& {\displaystyle \le 4.}\hfill \end{array}}$ Az egyenlet jobb oldalát vizsgálva, közben használva egy számtani-mértani közép közti egyenlőtlenséget a pozitív $\text{log}{}_2\left(x+1\right)$ kifejezésre: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{4}{\text{log}{}_2\left(x+1\right)}+\frac{\text{log}{}_2{\left(x+1\right)}^2}{2}=}\hfill \\ \hfill {\displaystyle =\frac{4}{\text{log}{}_2\left(x+1\right)}+\text{log}{}_2\left(x+1\right)\ge 2\sqrt[]{\frac{4}{\text{log}{}_2\left(x+1\right)}\cdot \text{log}{}_2\left(x+1\right)}=2\sqrt[]{4}=\mathrm{4,}}\hfill \end{array}}$ azaz $\begin{array}{c}{\displaystyle \frac{4}{\text{log}{}_2\left(x+1\right)}+\frac{\text{log}{}_2{\left(x+1\right)}^2}{2}\ge 4.}\end{array}$ Kaptuk, hogy az egyenlet bal oldala 4 vagy kisebb, a jobb oldala 4 vagy nagyobb. Egyenlőség akkor és csak akkor lehet, ha mind a két oldal 4, ekkor ${\displaystyle \begin{array}{cccc}\hfill {\displaystyle x^2-6x+13={\left(x-3\right)}^2+4}& {\displaystyle =\mathrm{4,}}\hfill & {\displaystyle \frac{4}{\text{log}{}_2\left(x+1\right)}}\hfill & \hfill {\displaystyle =\text{log}{}_2\left(x+1\right)\mathrm{,}}\\ \hfill {\displaystyle {\left(x-3\right)}^2}& {\displaystyle =\mathrm{0,}}\hfill & {\displaystyle \text{log}{}_2^2\left(x+1\right)}\hfill & \hfill {\displaystyle =\mathrm{4,}}\\ \hfill {\displaystyle x_1}& {\displaystyle =\mathrm{3,}}\hfill & {\displaystyle \text{log}{}_2\left(x+1\right)}\hfill & \hfill {\displaystyle =\pm \mathrm{2,}}\\ \hfill {\displaystyle }& {\displaystyle }\hfill & {\displaystyle x_2=\mathrm{3,}{x}_3}\hfill & \hfill {\displaystyle =-\frac{3}{4}\mathrm{.}}\end{array}}$ Mindkét követelmény csak az $x=3$ esetén teljesül, így ez az egyenlet megoldása. A kapott gyököt az ellenőrzés jónak találja. $b)$ Legyen $p$ annak a valószínűsége, hogy hatost dobunk, ekkor a többi dobásra $1-p$ adódik. Annak a valószínűsége, hogy 60 dobásból 15 esetben kapunk hatost: $\begin{array}{c}{\displaystyle P\left(\text{15 a 60-ból}\right)=\left(\genfrac{}{}{0ex}{}{60}{15}\right)p^{15}{\left(1-p\right)}^{45}\mathrm{.}}\end{array}$ Tekinthetjük ezt egy binomiális eloszlásnak. A várható érték $np$, ami az adott esetben $60\cdot p=15$, $p=\frac{1}{4}$. Ez az elvi $\frac{1}{6}$ értéktől erős eltérést mutat. Mindenképpen igazolja a gyanút, hogy ,,cinkelt'' a kocka.   4. $a)$ Egy nem állandó számtani sorozat első, második és negyedik eleméhez rendre $1$-et adunk, így egy mértani sorozat második, harmadik és negyedik elemét kapjuk. A mértani sorozat első, második és harmadik elemének az összege $7$. Mennyi a számtani sorozat $1010$-edik eleme?  (6 pont) $b)$ Adott a következő sorozat: $\begin{array}{c}{\displaystyle a_1=1;a_{n+1}=3\cdot a_n+1\left(n\ge 1\right)\mathrm{.}}\end{array}$ Adjuk meg a sorozat $2020$-adik tagját.  (7 pont)   Megoldás. $a)$ Jelöljük a számtani sorozat első elemét $a$-val és a differenciáját $d$-vel. Ekkor az első négy eleme rendre $a_1=a$; $a_2=a+d$; $a_2=a+2d$; $a_4=a+3d$. Az első, második és negyedik elemhez 1-et adva egy mértani sorozat egymás utáni három elemét kapjuk, amelyekre igaz, hogy a középső elem négyzete a két szélső szorzata, azaz: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left(a+d+1\right)}^2}& {\displaystyle =\left(a+1\right)\left(a+3d+1\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle a^2+d^2+1+2a+2d+2ad}& {\displaystyle =a^2+2a+1+3ad+3d\mathrm{,}}\hfill \\ \hfill {\displaystyle d^2-ad-d}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle d\left(d-a-1\right)}& {\displaystyle =0.}\hfill \end{array}}$ Mivel a sorozat nem állandó, ezért $d\ne 0$, így $d=a+1$. A számtani sorozat: $a_1=a$; $a_2=a+d=2a+1$; $a_3=3a+2$; $a_4=4a+3$. Az elemekhez egyet hozzáadva: $\begin{array}{c}{\displaystyle a_1=a+1;a_2=2a+2;a_3=3a+3;a_4=4a+4.}\end{array}$ Ezek közül az első, második és negyedik tényleg egy mértani sorozat elemei, melynek a hányadosa $q=2$. Az első, második és harmadik elem összege 7 a feladat szerint, tehát $\begin{array}{c}{\displaystyle \frac{a+1}{2}+\left(a+1\right)+2\left(a+1\right)=\mathrm{7,}\left(a+1\right)\cdot \frac{7}{2}=\mathrm{7,}a=1.}\end{array}$ Ekkor $d=2$, a kezdeti számtani sorozat 1; 3; 5; 7. Az elemekhez egyet adva a 2; 4; 6; 8 számokat kapjuk és a 2; 4; 8 tényleg egy mértani sorozat elemei. A $2$ előtti elem $1$, és az első három összege $1+2+4=7$. A számtani sorozat $1010$-edik eleme: $a_{1010}=1+1009\cdot 2=2019$. $b)$ I. megoldás. Az elemeket kiszámolva kapjuk, hogy $a_1=1$; $a_2=4$; $a_3=13$; $a_4=40$; $a_5=121$. Azt vehetjük észre, hogy ha a sorozat elemeit megszorozzuk 2-vel: $\begin{array}{c}{\displaystyle 2\cdot a_1=2;2\cdot a_2=8;2\cdot a_3=26;2\cdot a_4=80;2\cdot a_5=\mathrm{242,}}\end{array}$ akkor mindig egy három hatványnál eggyel kisebb számot kapunk. Tehát az a sejtés, hogy $a_n=\frac{3^n-1}{2}$. Alkalmazva a képzési szabályt: $\begin{array}{c}{\displaystyle a_{n+1}=3\cdot a_n+1=3\cdot \frac{3^n-1}{2}+1=\frac{3^{n+1}-3}{2}+1=\frac{3^{n+1}-1}{2}\mathrm{,}}\end{array}$ azaz igaz volt sejtésünk. Így a keresett elem: $\begin{array}{c}{\displaystyle a_{2020}=\frac{3^{2020}-1}{2}\mathrm{.}}\end{array}$ II. megoldás. Alakítsuk át az összefüggést: $\begin{array}{c}{\displaystyle a_{n+1}=3\cdot a_n+\mathrm{1,}{a}_{n+1}+\frac{1}{2}=3\cdot a_n+\frac{3}{2}\mathrm{,}{a}_{n+1}+\frac{1}{2}=3\cdot \left(a_n+\frac{1}{2}\right)\mathrm{.}}\end{array}$ Ezt felírva $n$-től $2$-ig: ${\displaystyle \begin{array}{cccccc}\hfill {\displaystyle a_n+\frac{1}{2}}& {\displaystyle =3\cdot \left(a_{n-1}+\frac{1}{2}\right)\mathrm{,}}\hfill & {\displaystyle }\hfill & \hfill {\displaystyle }& {\displaystyle a_{n-1}+\frac{1}{2}}\hfill & {\displaystyle =3\cdot \left(a_{n-2}+\frac{1}{2}\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle a_{n-2}+\frac{1}{2}}& {\displaystyle =3\cdot \left(a_{n-3}+\frac{1}{2}\right)\mathrm{,}}\hfill & {\displaystyle }\hfill & \hfill {\displaystyle \text{...}}& {\displaystyle a_2+\frac{1}{2}}\hfill & {\displaystyle =3\cdot \left(a_1+\frac{1}{2}\right)\mathrm{,}}\hfill \end{array}}$ majd összeszorozva $\begin{array}{c}{\displaystyle a_n+\frac{1}{2}=3^{n-1}\cdot \left(a_1+\frac{1}{2}\right)=3^{n-1}\cdot \frac{3}{2}=\frac{1}{2}\cdot 3^n\mathrm{,}{a}_n=\frac{3^n-1}{2}\mathrm{,}}\end{array}$ és innen $\begin{array}{c}{\displaystyle a_{2020}=\frac{3^{2020}-1}{2}\mathrm{.}}\end{array}$ III. megoldás (vázlat/ötlet). Az elemeket kiszámolva $a_1=1$; $a_2=4$; $a_3=13$; $a_4=40$; $a_5=121$. Észrevehető, hogy a sorozat elemeinek különbsége $\begin{array}{c}{\displaystyle a_2-a_1=3;a_3-a_2=9;a_4-a_3=27;a_5-a_4=\mathrm{81,}}\end{array}$ vagyis minden különbség az előző különbség háromszorosa, ami adódik az $\begin{array}{c}{\displaystyle \{{\displaystyle \begin{array}{cc}\hfill {\displaystyle a_n}& {\displaystyle =3\cdot a_{n-1}+1}\hfill \\ \hfill {\displaystyle a_{n-1}}& {\displaystyle =3\cdot a_{n-2}+1}\hfill \end{array}}\Rightarrow a_n-a_{n-1}=3a_{n-1}-3a_{n-2}=3\left(a_{n-1}-a_{n-2}\right)}\end{array}$ átalakításból is. Innen az elemek: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a_1}& {\displaystyle =\mathrm{1,}{a}_2=1+\mathrm{3,}{a}_3=1+3+3^2\mathrm{,}{a}_4=1+3+3^2+3^3\mathrm{,}\text{...}}\hfill \\ \hfill {\displaystyle a_n}& {\displaystyle =1+3+3^2+\text{...}+3^{n-1}\mathrm{,}}\hfill \end{array}}$ és adódik a zárt alak.   II. rész     5. $a)$ Legyen $a$ és $b$ nemnegatív valós szám. Bizonyítsuk be, hogy $\begin{array}{c}{\displaystyle 0\le \frac{\left(a+1\right)\left(b+1\right)}{a^2+b^2+2}\le 1.}\end{array}$ Írhatunk-e a nulla helyett nála nagyobb számot?  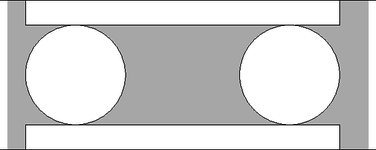(9 pont) $b)$ Egy felül nyitott fémdobozt lemezből állítunk elő úgy, hogy az 1. ábrán látható módon kivágunk, majd összehajtogatunk egy ilyen alakot. 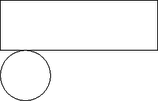  1. ábra  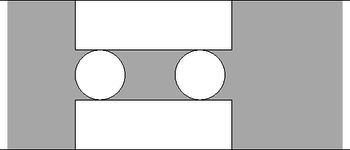 2. ábra A kivágást egy 30 cm-es széles fémszalagból végezzük úgy, hogy $2$ ilyen mintát fordítunk egymással szembe a 2. ábra szerint. Hogyan válasszuk meg a méreteket, hogy a kikerülő fémdoboz a lehető legnagyobb térfogatú legyen?  (7 pont)   Megoldás. $a)$ A nevező biztosan pozitív, hiszen $a^2+b^2+2\ge 2>0$. Nézzük a dupla egyenlőtlenség bal oldalát. A vizsgálandó kifejezés számlálója és nevezője is pozitív, így maga a tört is. Legyen $a$ kicsi és $b=n$ nagy szám. Ekkor ${\displaystyle \begin{array}{c}\hfill {\displaystyle 0\le \frac{\left(a+1\right)\left(b+1\right)}{a^2+b^2+2}=\frac{\left(a+1\right)\left(n+1\right)}{a^2+n^2+2}<\frac{2\cdot \left(n+1\right)}{n^2-1}=\frac{2\left(n+1\right)}{\left(n+1\right)\left(n-1\right)}=\frac{2}{n-1}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{\left(a+1\right)\left(b+1\right)}{a^2+b^2+2}<\frac{2}{b-1}\mathrm{,}0\le \frac{\left(a+1\right)\left(b+1\right)}{a^2+b^2+2}<\frac{2}{b-1}\mathrm{,}}\hfill \end{array}}$ ami azt jelenti, hogy a tört akármilyen kicsi tud lenni, így a bal oldalon nem lehet nulla helyett nagyobb számot írni. Egyenlőség semmilyen $a$, $b$ érték esetén nem teljesül. Rendezzük az egyenlőtlenség jobb oldalát: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{\left(a+1\right)\left(b+1\right)}{a^2+b^2+2}}& {\displaystyle \le \mathrm{1,}}\hfill \\ \hfill {\displaystyle \left(a+1\right)\left(b+1\right)}& {\displaystyle \le a^2+b^2+\mathrm{2,}}\hfill \\ \hfill {\displaystyle ab+a+b+1}& {\displaystyle \le a^2+b^2+\mathrm{2,}}\hfill \\ \hfill {\displaystyle ab+a+b}& {\displaystyle \le a^2+b^2+\mathrm{1,}}\hfill \\ \hfill {\displaystyle 2a+2b+2ab}& {\displaystyle \le 2a^2+2b^2+\mathrm{2,}}\hfill \\ \hfill {\displaystyle 0}& {\displaystyle \le a^2-2a+1+b^2-2b+1+a^2-2ab+b^2\mathrm{,}}\hfill \\ \hfill {\displaystyle 0}& {\displaystyle \le {\left(a-1\right)}^2+{\left(b-1\right)}^2+{\left(a-b\right)}^2\mathrm{.}}\hfill \end{array}}$ Az utolsó sor biztosan igaz, hiszen három szám négyzetének összege nem lehet negatív. Mivel a lépések megfordíthatóak, ezért az eredeti egyenlőtlenség is igaz. Egyenlőség akkor és csak akkor teljesül, ha egyidejűleg mind a három négyzetszám nulla, azaz $a=b=1$. $b)$ Legyen a kivágandó körlemez sugara $r$, ekkor a fémdoboz magassága $\begin{array}{c}{\displaystyle m=\frac{30-2r}{2}=15-r}\end{array}$ lesz. A térfogata $V=r^{2}m\pi =r^2\left(15-r\right)\pi$, ahol $0\le r\le 15$. Tekintsük az $f:\left[0;15\right]\to \text{R}$; $x\mapsto x^2\left(15-x\right)$ függvényt. Ennek keressük a maximumát. Egy zárt intervallumon folytonos függvénynek van szélsőértéke. Mivel $f\left(0\right)=f\left(15\right)=0$, ezért a maximumát az intervallum belső pontjában veszi fel. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle f\left(x\right)}& {\displaystyle =x^2\left(15-x\right)=15x^2-x^3\mathrm{,}}\hfill \\ \hfill {\displaystyle f\text{'}\left(x\right)}& {\displaystyle =30x-3x^2\mathrm{,}}\hfill \\ \hfill {\displaystyle f\text{'}\text{'}\left(x\right)}& {\displaystyle =30-6x\mathrm{.}}\hfill \end{array}}$ Ott lehet maximuma, ahol $f\text{'}\left(x\right)=0$ és $f\text{'}\text{'}\left(x\right)<0$. $\begin{array}{c}{\displaystyle f\text{'}\left(x\right)=30x-3x^2=3x\left(10-x\right)=0.}\end{array}$ Csak az $x=10$ jöhet szóba, ekkor $f\text{'}\text{'}\left(10\right)=30-6\cdot 10=-30<0$; azaz $x=10$-ben tényleg maximuma van a függvénynek, a maximális értéke $f\left(10\right)={10}^2\left(15-10\right)=500$. Kaptuk, hogy $V=r^2\left(15-r\right)\pi \le 500\pi$ és a maximuma $r=10$ esetén lesz, a térfogata ekkor $500\pi {\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^3$. A méretarányos rajz ezek szerint:         6. $a)$ Adjuk meg annak az egyenesnek az egyenletét, mely egyidejűleg érinti az $y=x^2$ és $y=-x^2+4x-2$ parabolákat.  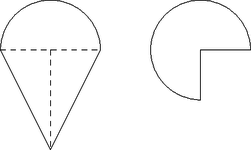(9 pont) $b)$ A magyar GúgLi Kft. egy emblémát tervez a székházuk elé, amely egy félbevágott gömb és egy kúp összetételéből áll. Az emblémának függőlegesen a negyede ki van vágva úgy, hogy a két vágósík az embléma függőleges tengelye mentén metszi egymást. Az embléma keresztmetszete és a függőleges metszete az ábrán látható.     A kúp magassága éppen a félbevágott gömb sugarának a kétszerese. Betonból szeretnék elkészíttetni majd lefesteni a 1,5 m magasságúra tervezett emblémát. ‐ Mennyi beton szükséges az elkészítéséhez, ha az elkészítés folyamán $15\%$ veszteséggel számolhatunk? ‐ Mekkora lesz az elkészült embléma tömege? ‐ Hány ${\text{m}}^2$-re elegendő festéket kell beszerezniük, ha az időjárás ellen háromszor szeretnék lefesteni és a festés során keletkező veszteség $5\%?$  (7 pont)   Megoldás. $a)$ I. megoldás. Határozzuk meg egy $a$ pontban az $y=x^2$ érintőjét. Az érintő meredeksége: $y\text{'}=2x$; $m=2a$. Ez átmegy az $\left(a;a^2\right)$ ponton, így az érintő: $y=2a\left(x-a\right)+a^2=2ax-a^2$. Ezen egyenesnek és az $y=-x^2+4x-2$ parabolának 1 metszéspontja (érintési pont) van. Keressük ezt meg, azaz oldjuk meg a következő egyenletrendszert: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \{{\displaystyle \begin{array}{c}\hfill {\displaystyle y=2ax-a^2\mathrm{,}}\\ \hfill {\displaystyle y=-x^2+4x-2.}\end{array}}}\hfill \\ \hfill {\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle 2ax-a^2}& {\displaystyle =-x^2+4x-\mathrm{2,}}\hfill \\ \hfill {\displaystyle x^2+\left(2a-4\right)x-\left(a^2-2\right)}& {\displaystyle =0.}\hfill \end{array}}}\hfill \end{array}}$ Mivel az egyenes érintő, ennek a másodfokú egyenletnek csak egy valós szám lehet a megoldása, tehát a diszkriminánsa nulla: $\begin{array}{c}{\displaystyle 0=D={\left(2a-4\right)}^2+4\left(a^2-2\right)=8a^2-16a+8=8{\left(a-1\right)}^2\mathrm{,}}\end{array}$ vagyis $a=1$ és a keresett érintő $y=2x-1$. II. megoldás. Határozzuk meg egy $a$ pontban az $y=x^2$ érintőjét. Az érintő meredeksége: $y\text{'}=2x$; $m=2a$. Ez átmegy az $\left(a;a^2\right)$ ponton, így az érintő $\begin{array}{c}{\displaystyle y=2a\left(x-a\right)+a^2=2ax-a^2\mathrm{.}}\end{array}$ Határozzuk meg most egy $b$ pontban az $y=-x^2+4x-2$ érintőjét. Az érintő meredeksége: $y\text{'}=-2x+4$, $m=-2b+4$. Ez átmegy a $\left(b;-b^2+4b-2\right)$ ponton, így az érintő: $\begin{array}{c}{\displaystyle y=\left(-2b+4\right)\left(x-b\right)-b^2+4b-2=\left(-2b+4\right)x+b^2-2.}\end{array}$ Ha közös az érintő, akkor ugyanaz az egyenes egyenlete, azaz ${\displaystyle \begin{array}{c}\hfill {\displaystyle y=2ax-a^2\mathrm{,}y=\left(-2b+4\right)x+b^2-2.}\hfill \\ \hfill {\displaystyle \{{\displaystyle \begin{array}{c}\hfill {\displaystyle 2a=-2b+\mathrm{4,}}\\ \hfill {\displaystyle -a^2=b^2-2.}\end{array}}}\hfill \end{array}}$ Megoldva az egyenletrendszert: ${\displaystyle \begin{array}{c}\hfill {\displaystyle 2a=-2b+\mathrm{4,}a=-b+\mathrm{2,}-{\left(-b+2\right)}^2=b^2-\mathrm{2,}}\hfill \\ \hfill {\displaystyle -b^2+4b-4=b^2-\mathrm{2,}0=2b^2-4b+\mathrm{2,}0=b^2-2b+1={\left(b-1\right)}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle b=\mathrm{1,}a=1.}\hfill \end{array}}$ Innen a közös érintő: $y=2x-1$. $b)$ A félgömb sugara legyen $r$, ekkor a kúp magassága $2r$. Az egész embléma magassága így $3r$, ami a feladat szerint 1,5 m: $3r=1\mathrm{,}5$, $r=0\mathrm{,}5$. Nézzük a térfogatot. A kivágott félgömb térfogata: $\begin{array}{c}{\displaystyle V_{\text{félgömb}}=\frac{4r^3\pi }{3}\cdot \frac{1}{2}\cdot \frac{3}{4}=\frac{r^3\pi }{2}\mathrm{.}}\end{array}$ A kivágott kúp térfogata: $\begin{array}{c}{\displaystyle V_{\text{kúp}}=\frac{r^2\pi \cdot 2r}{3}\cdot \frac{3}{4}=\frac{r^3\pi }{2}\mathrm{.}}\end{array}$ Az embléma térfogata: $\begin{array}{c}{\displaystyle V_{\text{embléma}}=V_{\text{félgömb}}+V_{\text{kúp}}=\frac{r^3\pi }{2}+\frac{r^3\pi }{2}=r^3\pi \mathrm{.}}\end{array}$ Ez a beton térfogatának a $85\%$-a: $\begin{array}{c}{\displaystyle 0\mathrm{,}85\cdot V_{\text{beton}}=r^3\pi \mathrm{,}{V}_{\text{beton}}=r^3\pi \cdot \frac{20}{17}\approx 0\mathrm{,}462{\text{m}}^3\mathrm{.}}\end{array}$ Az embléma tömege ($2400{\text{kg/m}}^3$-es beton sűrűséget használva) $0\mathrm{,}462\cdot 2400=1108\mathrm{,}8$ kg. Nézzük a felszínt. A kivágott félgömb felszíne: $\begin{array}{c}{\displaystyle A_{\text{félgömb}}=\frac{4r^2\pi }{2}\cdot \frac{3}{4}+\frac{r^2\pi }{2}=2r^2\pi \mathrm{.}}\end{array}$ Az alkotó $r\sqrt[]{5}$, így a kivágott kúp felszíne: $\begin{array}{c}{\displaystyle A_{\text{kúp}}=\frac{2r\pi \cdot \sqrt[]{5}r}{2}\cdot \frac{3}{4}+2\cdot \frac{2r\cdot r}{2}=\frac{3r^2\pi \cdot \sqrt[]{5}}{4}+2r^2=\frac{3\pi \cdot \sqrt[]{5}+8}{4}\cdot r^2\mathrm{.}}\end{array}$ Az embléma felszíne: $\begin{array}{c}{\displaystyle A_{\text{embléma}}=A_{\text{félgömb}}+A_{\text{kúp}}=2r^2\pi +\frac{3\pi \cdot \sqrt[]{5}+8}{4}\cdot r^2=\frac{3\pi \cdot \sqrt[]{5}+8\pi +8}{4}\cdot r^2\mathrm{.}}\end{array}$ Háromszor kell festeni és a festék $95\%$-a hasznosul: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 0\mathrm{,}95\cdot A_{\text{festék}}}& {\displaystyle =3\cdot \frac{3\pi \cdot \sqrt[]{5}+8\pi +8}{4}\cdot r^2\mathrm{,}}\hfill \\ \hfill {\displaystyle A_{\text{festék}}}& {\displaystyle =60\cdot \frac{3\pi \cdot \sqrt[]{5}+8\pi +8}{76}\cdot r^2\approx 10\mathrm{,}7{\text{m}}^2\mathrm{.}}\hfill \end{array}}$   7. $a)$ $18$ tudós e-mail segítségével tartja a kapcsolatot a világban. Bármely két tudós egymással angol, német vagy orosz nyelven levelezik, mindig ugyanazt a nyelvet használják egymás között. Tudjuk, hogy nincs három olyan tudós, aki egymás között angol, vagy orosz nyelvet használ. Bizonyítsuk be, hogy létezik közöttük három, akik egymással németül leveleznek.  (9 pont) $b)$ Aladár négyjegyű számokat ír fel egy papírlapra, melyek csak az 1; 2; 3 és $4$ számjegyeket tartalmazhatják (lehet ismétlődés, nem kell minden számjegyet felhasználni minden négyjegyű számban). Figyel arra, hogy $1$-es után csak $4$-es, páros számjegy után csak páratlan jegy következhet. Hányféle számot tud leírni így?   (7 pont)   Megoldás. $a)$ A feladatot általánosan oldjuk meg: ha 18 tudós 3 nyelvet használ, akkor biztosan van olyan nyelv, amit 3 tudós egymás között használ. A használt nyelvek legyenek $A$, $B$ és $C$. Tekintsük az egyik tudóst, ő 17 másikkal levelez. A skatulyaelv miatt lesz olyan nyelv (legyen ez az $A$ nyelv), amin legalább 6 másik tudóssal levelez. Ha a 6 levelező partner között van kettő, akik egymással az $A$ nyelven leveleznek, akkor készen vagyunk, hiszen találtunk három tudóst, aki az $A$ nyelven leveleznek egymás között. Ha ez nem teljesül, akkor ez a 6 tudós egymás között csak a $B$ és $C$ nyelvet használja. Tekintsünk most ebből a hat tudósból egyet, aki a másik öttel levelez. A skatulyaelv miatt biztosan van olyan nyelv (legyen ez a $B$ nyelv), amit legalább 3 másikkal használ. Ezen másik három most egymás között ha használja a $B$ nyelvet, akkor találunk három tudóst, aki a $B$ nyelvet használja, ha meg nem, akkor ők egymás között a $C$ nyelvet használják, és ezért vagyunk készen. Ezt a feladatra alkalmazva adódik az állítás.   $b)$ Építsük fel balról jobbra a számokat. Jelölje $f_1\left(n\right)$ az $n$ hosszúság esetén az 1-esre végződő számok számát. Jelölje $f_2\left(n\right)$ az $n$ hosszúság esetén az 2-esre végződő számok számát. Jelölje $f_3\left(n\right)$ az $n$ hosszúság esetén az 3-asre végződő számok számát. Jelölje $f_4\left(n\right)$ az $n$ hosszúság esetén az 4-esre végződő számok számát. Ekkor ${\displaystyle \begin{array}{cc}\hfill {\displaystyle f_1\left(1\right)}& {\displaystyle =f_2\left(1\right)=f_3\left(1\right)=f_4\left(1\right)=1\text{és}}\hfill \\ \hfill {\displaystyle f_1\left(2\right)}& {\displaystyle =f_2\left(1\right)+f_3\left(1\right)+f_4\left(1\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle f_2\left(2\right)}& {\displaystyle =f_3\left(1\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle f_3\left(2\right)}& {\displaystyle =f_2\left(1\right)+f_3\left(1\right)+f_4\left(1\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle f_4\left(2\right)}& {\displaystyle =f_1\left(1\right)+f_3\left(1\right)\mathrm{,}\text{illetve}}\hfill \\ \hfill {\displaystyle f_1\left(n+1\right)}& {\displaystyle =f_2\left(n\right)+f_3\left(n\right)+f_4\left(n\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle f_2\left(n+1\right)}& {\displaystyle =f_3\left(n\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle f_3\left(n+1\right)}& {\displaystyle =f_2\left(n\right)+f_3\left(n\right)+f_4\left(n\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle f_4\left(n+1\right)}& {\displaystyle =f_1\left(n\right)+f_3\left(n\right)\mathrm{.}}\hfill \end{array}}$ Táblázatba foglalva:   ${\displaystyle \begin{array}{|cccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>n</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>f</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>n</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>f</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>n</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>f</mi></mrow><mrow><mn>3</mn></mrow></msub></mrow><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>n</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>f</mi></mrow><mrow><mn>4</mn></mrow></msub></mrow><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>n</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math> }}\hfill & \hfill {\displaystyle \text{ Összes }}\hfill \\ \hfill {\displaystyle \text{1 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill \\ \hfill {\displaystyle \text{2 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 9 }}\hfill \\ \hfill {\displaystyle \text{3 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 21 }}\hfill \\ \hfill {\displaystyle \text{4 }}\hfill & \hfill {\displaystyle \text{ 15 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 15 }}\hfill & \hfill {\displaystyle \text{ 12 }}\hfill & \hfill {\displaystyle \text{ 48 }}\hfill \\ \hline\end{array}}$   Tehát 48 ilyen számot tud felírni.   Megjegyzés. Ha $S_n$-nel jelöljük az összeget, akkor arra igaz, hogy $\begin{array}{c}{\displaystyle S_1=4;S_2=9;S_n=S_{n-1}+3\cdot S_{n-2};n\ge 3.}\end{array}$   8. $a)$ Oldjuk meg a következő egyenletet a pozitív egészek halmazán: $\begin{array}{c}{\displaystyle 2\cdot \left(x;y\right)+17\cdot \left[x;y\right]=\mathrm{257,}}\end{array}$ ahol a ,,kerek'' zárójel a két szám legnagyobb közös osztóját, a ,,szögletes'' zárójel pedig a legkisebb közös többszörösét jelöli.  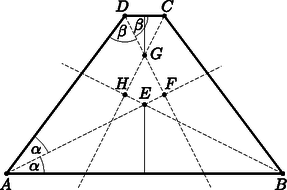(9 pont) $b)$ Egy szimmetrikus trapéz párhuzamos oldalai $2$ és $14$, szárai $10$ egység hosszúak. Meghúzzuk a belső szögeinek szögfelezőjét, amelyek egy négyszöget zárnak be. Amennyiben ennek a négyszögnek létezik a beírt és körülírt köre, mekkora ezen körök sugara?  (7 pont)   Megoldás. $a)$ A legnagyobb közös osztóban a közös prímek, a legkisebb közös többszörösben az összes prím, tehát a legnagyobb közös osztó prímjei is szerepelnek; és a legnagyobb közös osztóban levő prímek kitevője nem lehet nagyobb a legkisebb közös többszörösben szereplő prímek kitevőjénél. Ezért $\left(x;y\right)\mid \left[x;y\right]$. Az egyenlet bal oldala osztható $\left(x;y\right)$-nal, tehát a jobb oldal is: $\left(x;y\right)\mid 257$. Mivel 257 prím, ezért két eset van. I. eset: $\left(x;y\right)=257$. $\begin{array}{c}{\displaystyle 2\cdot \left(x;y\right)+17\cdot \left[x;y\right]=\mathrm{257,}2\cdot 257+17\cdot \left[x;y\right]=\mathrm{257,}17\cdot \left[x;y\right]=-257.}\end{array}$ Ekkor a legkisebb közös többszörösre negatív szám adódik (de még egésznek sem egész), tehát ez nem lehet. II. eset: $\left(x;y\right)=1$. ${\displaystyle \begin{array}{cccc}\hfill {\displaystyle 2\cdot \left(x;y\right)+17\cdot \left[x;y\right]}& {\displaystyle =\mathrm{257,}}\hfill & {\displaystyle }\hfill & \hfill {\displaystyle 2\cdot 1+17\cdot \left[x;y\right]=\mathrm{257,}}\\ \hfill {\displaystyle 17\cdot \left[x;y\right]}& {\displaystyle =\mathrm{255,}}\hfill & {\displaystyle }\hfill & \hfill {\displaystyle \left[x;y\right]=\mathrm{15,}}\end{array}}$ azaz olyan számokat keresünk, amelyek relatív prímek és csak $3$-as és $5$-ös prímeket tartalmazhatnak, mert a legkisebb közös többszörös a 15. Négy lehetőség van: ${\displaystyle \begin{array}{|ccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi></math> }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 15 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 5}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi></math> }}\hfill & \hfill {\displaystyle \text{ 15 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 3}}\hfill \\ \hline\end{array}}$   $b)$ Készítsünk ábrát. Jelöljünk meg pár szöget és bocsássunk merőlegest a $G$ és $E$ pontokból a megfelelő alapokra. A trapéz magassága $\begin{array}{c}{\displaystyle {10}^2=m^2+{\left(\frac{14-2}{2}\right)}^2\Rightarrow m=8.}\end{array}$ A szögekre pedig $\begin{array}{c}{\displaystyle \text{tg}2\alpha =\frac{8}{6}=\frac{4}{3};\alpha +\beta ={90}^{\circ }\mathrm{.}}\end{array}$     A szimmetrikus trapéz miatt a keletkezett négyszög szimmetrikus a $GE$ egyenesre és konvex, tehát deltoid. A konvex deltoidoknak van beírt köre (szembeni oldalak összege megegyezik). $AFD\sphericalangle =BHC\sphericalangle ={90}^{\circ }$, ugyanis a trapéz egy szárán levő szögek összege ${180}^{\circ }$, így a szögfelezők ${90}^{\circ }$-os szöget zárnak be. Tehát a négyszögünk 2 szemközti szögének összege ${180}^{\circ }$, így van köré írt köre is. Derékszögű háromszögekben számolva: ${\displaystyle \begin{array}{cccccc}\hfill {\displaystyle AE}& {\displaystyle =\frac{7}{\text{cos}\alpha }\mathrm{,}}\hfill & {\displaystyle AF}\hfill & \hfill {\displaystyle =10\cdot \text{cos}\alpha \mathrm{,}}& {\displaystyle EF}\hfill & {\displaystyle =10\cdot \text{cos}\alpha -\frac{7}{\text{cos}\alpha }\mathrm{,}}\hfill \\ \hfill {\displaystyle DG}& {\displaystyle =\frac{1}{\text{cos}\beta }\mathrm{,}}\hfill & {\displaystyle DF}\hfill & \hfill {\displaystyle =10\cdot \text{cos}\beta \mathrm{,}}& {\displaystyle GF}\hfill & {\displaystyle =10\cdot \text{cos}\beta -\frac{1}{\text{cos}\beta }\mathrm{.}}\hfill \end{array}}$ $EFG▵$ derékszögű és az átfogója a négyszög köré írt kör sugarának a kétszerese, azaz $\begin{array}{c}{\displaystyle {\left(2R\right)}^2=E{F}^2+G{F}^2\Rightarrow R=\frac{1}{2}\cdot \sqrt[]{E{F}^2+G{F}^2}\mathrm{.}}\end{array}$ A beírt körre igaz, hogy $\begin{array}{c}{\displaystyle t=\frac{k\cdot r}{2}\mathrm{,}2\cdot \frac{EF\cdot GF}{2}=r\cdot \frac{\left(2\cdot EF+2\cdot GF\right)}{2}\mathrm{,}r=\frac{EF\cdot GF}{EF+GF}\mathrm{.}}\end{array}$ Az adatokat behelyettesítve kapjuk: $r=0\mathrm{,}745$; $R=1\mathrm{,}25$.   9. $a)$ Bizonyítsuk be, hogy ${\displaystyle \begin{array}{c}\hfill {\displaystyle 1\cdot 2+2\cdot 3+\text{...}+n\cdot \left(n+1\right)=}\\ \hfill {\displaystyle =\frac{n\cdot \left(n+1\right)\cdot \left(n+2\right)}{3}\mathrm{,}}\end{array}}$ ahol $n\in {\text{N}}^{+}$.  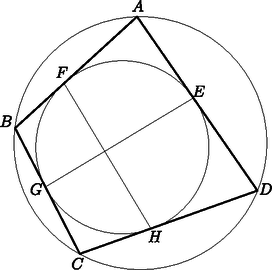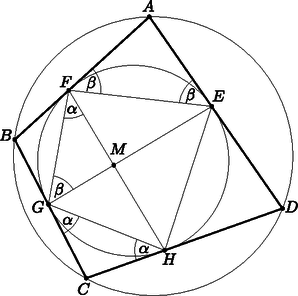(8 pont) $b)$ Adott egy olyan húrnégyszög, ami egyben érintőnégyszög is. Az ábrán jelöltük az érintési pontokat. Bizonyítsuk be, hogy az $EG$ és $FH$ szakaszok merőlegesek egymásra.   (8 pont)       Megoldás. $a)$ Teljes indukcióval bizonyítunk. I. Nézzük meg, hogy teljesül-e a bizonyítandó állítás az $n=1$ és $n=2$ esetre: ${\displaystyle \begin{array}{cccc}\hfill {\displaystyle n}& {\displaystyle =1}\hfill & {\displaystyle 1\cdot 2}\hfill & \hfill {\displaystyle =\frac{1\cdot 2\cdot 3}{3}=\mathrm{2,}}\\ \hfill {\displaystyle n}& {\displaystyle =2}\hfill & {\displaystyle 1\cdot 2+2\cdot 3}\hfill & \hfill {\displaystyle =\frac{2\cdot 3\cdot 4}{3}=8.}\end{array}}$ II. Tegyük fel, hogy $n=k$-ig minden értékre teljesül, hogy $\begin{array}{c}{\displaystyle 1\cdot 2+2\cdot 3+\text{...}+k\cdot \left(k+1\right)=\frac{k\cdot \left(k+1\right)\cdot \left(k+2\right)}{3}\mathrm{.}}\end{array}$ III. Nézzük az $n=k+1$ esetet, induljunk ki a bal oldalból: ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle 1\cdot 2}& {\displaystyle +2\cdot 3+\text{...}+k\cdot \left(k+1\right)+\left(k+1\right)\cdot \left(k+2\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={\displaystyle \frac{k\cdot \left(k+1\right)\cdot \left(k+2\right)}{3}}+\left(k+1\right)\cdot \left(k+2\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\left(k+1\right)\left(k+2\right)\left({\displaystyle \frac{k}{3}}+1\right)=\left(k+1\right)\left(k+2\right)\frac{k+3}{3}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={\displaystyle \frac{\left(k+1\right)\left(k+2\right)\left(k+3\right)}{3}}\mathrm{,}}\hfill \end{array}}}\hfill \\ \hfill {\displaystyle 1\cdot 2+2\cdot 3+\text{...}+k\cdot \left(k+1\right)+\left(k+1\right)\cdot \left(k+2\right)=\frac{\left(k+1\right)\left(k+2\right)\left(k+3\right)}{3}\mathrm{.}}\hfill \end{array}}$ Ezt akartuk kapni, tehát a bizonyítás kész. $b)$ Húzzuk meg a $FG$, $GH$, $HE$ és $EF$ szakaszokat. $HFG\sphericalangle =CGH\sphericalangle =CHG\sphericalangle =\alpha$, mivel mind a $GH$ szakasz kerületi vagy érintő szárú kerületi szögei. Tehát $GCH\sphericalangle ={180}^{\circ }-2\alpha$. $FEA\sphericalangle =EFA\sphericalangle =FGE\sphericalangle =\beta$, mivel mind az $FE$ szakasz kerületi vagy érintő szárú kerületi szögei. Tehát $EAF\sphericalangle ={180}^{\circ }-2\beta$. Mivel az $ABCD$ négyszög húrnégyszög, ezért a szemben fekvő szögeinek összege ${180}^{\circ }$, tehát $\begin{array}{c}{\displaystyle {180}^{\circ }-2\alpha +{180}^{\circ }-2\beta ={180}^{\circ }\mathrm{,}}\end{array}$ $2\alpha +2\beta ={180}^{\circ }$, $\alpha +\beta ={90}^{\circ }$. Innen $GMF\sphericalangle ={180}^{\circ }-\alpha -\beta ={90}^{\circ }$ és ezt kellett bizonyítani.