A koronavírus világjárvánnyá szélesedése bizonyára felkeltette a KöMaL olvasóinak érdeklődését a járványmodellek iránt. Ez az írás nekik szól: a legelterjedtebb (ún. SIR-féle) járványmodellt mutatjuk be. Bonyolultsága miatt mégis le kell mondanunk a koronavírus terjedésének valódi modellezéséről, tehát csak bevezetésre számítson az Olvasó.
Megnehezíti dolgunkat, hogy dinamikus folyamatról van szó, ahol minden pillanatban a már fertőzöttek egy része megfertőzi a még nem fertőzöttek (röviden: megfertőzhetők) bizonyos részét, miközben a fertőzöttek másik része meggyógyul vagy meghal. A szakirodalmat követve, ebben a leírásban a könnyebb érthetőség érdekében több végletes egyszerűsítő feltevést teszünk: $a)$ a népesség létszáma időben állandó; $b)$ a fertőzésben senki sem hal meg; $c)$ ha valaki kigyógyul a fertőzésből, az már nem fertőződik meg és nem fertőz újra; $d)$ a fertőzési valószínűség független a népesség egyéb (nemi, életkori, területi, egészségi állapot- stb.) jellemzőitől; $e)$ a gyógyulási valószínűség független az egészségügyi ellátástól.
Három típust különböztetünk meg: a megfertőzhetők (susceptibles, S), (népességi) részarányuk $s>0$; a fertőzöttek (infectious, I), részarányuk $i>0$; végül a gyógyultak (recovered, R), de ide tartoznak az eleve immunisak is: részarányuk $r>0$, innen a modell közkeletű elnevezése: SIR-modell. Az ilyen típusú modelleket egyébként rekeszmodelleknek nevezik.
Egyenleteinkben kulcsszerepet kap a fertőzési és a gyógyulási ráta. Ezek függvényében igazoljuk, hogy a megfertőzhetők részarányának kicsi kezdőértékeire elhal a járvány, és nagy kezdőértékeire fellángol. Azt is szemléltetni tudjuk, hogyan laposítja el a járvány időbeli lefutását, ha a fertőzési rátát elkülönítéssel vagy a megfertőzhetők részarányának kezdőértékét oltással csökkentjük.
A technikai egyszerűség kedvéért és a szokással ellentétben, nem folytonos, hanem diszkrét időben írjuk föl a népességi részarányok dinamikáját, egységnyinek rögzítve az időszak hosszát, pl. nap, hét, $t=\mathrm{0,1,2,}\text{...}$ az időszakok indexe. A jobb érthetőség kedvéért az $S\to I\to R$ időrendi sorrendet felcserélve adjuk meg a három egyenletet.
Föltesszük, hogy az új fertőzések részaránya egyaránt arányos a megfertőzhetők és a fertőzöttek részarányával, de az újonnan gyógyultak részaránya csak a fertőzöttek részarányával arányos. Visszatérve a ,,rekeszek tartalmára'':
A megfertőzhetők részarányának csökkenése egyenesen arányos a megfertőzhetők részarányának és a fertőzöttek részarányának szorzatával:

 

Bizonyítás. $a)$ Ha $s_0\le s^{\text{o}}$, akkor $s_t<s^{\text{o}}$ ($t>0$). Két alesetet különböztetünk meg.
$\left(i\right)$ Ha $s_0<s^{\text{o}}$, akkor (6)-ot felírva $\mathrm{0,1,}\text{...}\mathrm{,}t-1$ időszakra, és figyelembe véve, hogy $s_{t-1}<\cdots <s_1<s_0$, adódik

$\begin{array}{c}{\displaystyle i_t=\left[1+\beta \left(s_{t-1}-s^{\text{o}}\right)\right]\cdot \text{...}\cdot \left[1+\beta \left(s_0-s^{\text{o}}\right)\right]i_0<{\left[1+\beta \left(s_0-s^{\text{o}}\right)\right]}^t{i}_0\mathrm{,}}\end{array}$

(8i)

azaz $i_t$ gyorsan tart 0-hoz. $\left(ii\right)$ Ha $s_0=s^{\text{o}}$, akkor az első lépést külön kell kezelni. $i_1=i_0$, és (5) szerint $s_1=\left(1-\beta i_0\right)s^{\text{o}}$, majd (8i) szerint

$\begin{array}{c}{\displaystyle i_t<{\left[1+\beta \left(s_1-s^{\text{o}}\right)\right]}^{t-1}{i}_1={\left[1-{\beta }^2{i}_0{s}^{\text{o}}\right]}^{t-1}{i}_0\mathrm{,}t\ge 1.}\end{array}$

(8ii)

$b)$ $0<s^{\text{o}}<s_0<1$ esetén, amíg a megfertőzöttek részaránya nagyon kicsi: $i_t\approx 0$, addig (5) miatt $s_t\approx s_0$ (csak lassan csökken), tehát $i_t$ részarány (6) és $s^{\text{o}}<s_0<1$ miatt közelítőleg egy $1+\beta s_0-\gamma$-hányadosú mértani sorozat szerint nő. Belátjuk, hogy előbb-utóbb $s_t$ a kritikus érték alá süllyed, s $a)$ szerint $i_t$ ezután végleg csökkenésre vált.
Indirekt bizonyítunk. Tegyük föl, hogy $s_t\ge s^{\text{o}}$ minden $t$-re. Az $\left(s_t\right)$ alulról korlátos csökkenő sorozat, tehát van határértéke, amelyre $s^{*}\ge s^{\text{o}}$ áll. (6) szerint $i_t\ge i_0$, azaz (5) szerint $s_t\le {\left(1-\beta i_0\right)}^t{s}_0$, azaz $s^{*}=0$, s ez ellentmond $s^{*}\ge s^{\text{o}}>0$-nak.  $\square$
További vizsgálatot igényelne, hogy hosszú távon milyen esetben szűnik meg a megfertőzhetőség (és válik teljessé a gyógyultság), számpéldáinkban azonban az idők végezetéig maradnak megfertőzhetők.
Rátérünk a numerikus szemléltetésre. Önkényesen választjuk, hogy $i_0=0\mathrm{,}01$. Első futásunkban $\beta =1$ és $\gamma =1/3$, valamint a megfertőzhetők részarányának nagy kezdőértéket adunk: $s_0=0\mathrm{,}9>s^{\text{o}}=1/3$. Egyszerű programmal elkészíthetjük az 1. ábrát. Legérdekesebb eredmény: a 10. időszakban éri el a fertőzöttség a maximumát, a lakosság 27,7%-a fertőzött. A 20. időszakra a fertőzöttség gyakorlatilag eltűnik, de további számítások szerint a megfertőzhetőség megmarad 5%-nál.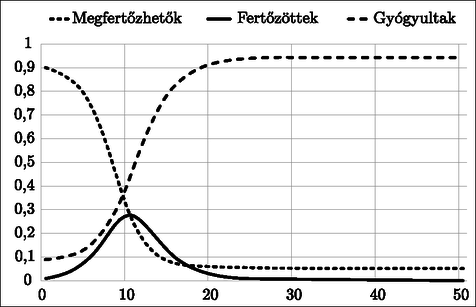

 

 

1. ábra. Erős fertőzés, sok megfertőzhető

 

A második futásban feltesszük, hogy elkülönítéssel sikerült az erős fertőzési rátát gyengíteni: $\beta =0\mathrm{,}5$. Az előző programot használva kapjuk a 2. ábrát. A legérdekesebb eredmény: a fertőzöttség jóval később, a 22. időszak körül éri el a maximumát, s a lakosságnak csupán 4,5%-a fertőzött, de a megfertőzhetők részaránya lassabban csökken, és megáll 45%-nál.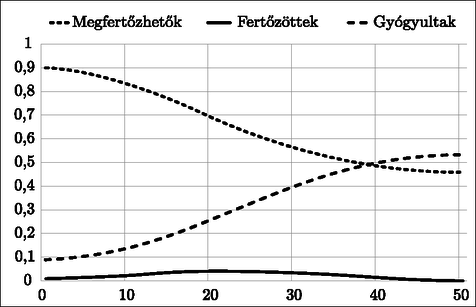

 

 

2. ábra. Gyengén fertőző, sok megfertőzhető

 

A harmadik futásnál feltesszük, hogy oltással sikerült a megfertőzhetők nagy kezdő-részarányát jelentősen csökkenteni, de a kritikus érték fölött maradva: $s_0=0\mathrm{,}5>s^{\text{o}}$. A fertőzési ráta újra nagy: $\beta =1$. A 3. ábrán látható, hogy a maximális fertőzöttség véletlenül ismét 4,4%, de már a 16. időszakban elérjük, és alacsonyabb lesz a megfertőzhetők részarányának határértéke: 19%.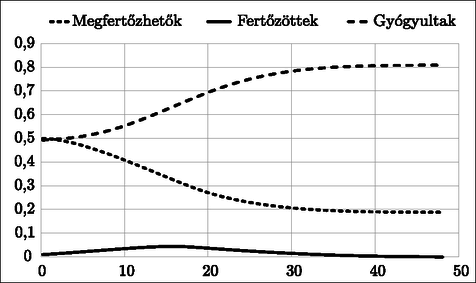

 

 

3. ábra. Erősen fertőző, kevés megfertőzhető

 

Eddig kizártuk a $\gamma \ge \beta$ esetet. A teljesség kedvéért most röviden megvizsgáljuk, mi történik ekkor. Formálisan $s^{\text{o}}\ge 1$, tehát az 1. tétel $b)$ pontja értelmében minden $s_0\le 1$ kezdőállapotra teljesül az $s_0\le s^{\text{o}}$ feltétel, azaz a járvány elhal.
Összefoglalásként, ne várjunk csodákat egy modelltől. Ez a modell csak a legegyszerűbb összefüggéseket képes megvilágítani, például, hogy létezik a megfertőzhetők részarányának egy kritikus értéke. Ha a kritikus érték alattról vagy fölöttről indítjuk a rendszert, az nemcsak kvantitatíve, de kvalitatíve is másképp viselkedik. Modellünk azonban képtelen kezelni a koronavírus-járványnak azt a központi kérdését, hogy az elkülönítés a fertőzési folyamat lassításával megnöveli a gyógyulás valószínűségét (lesz elég lélegeztetőgép). Ennek részletezése azonban túlmutat a tanulmányon.