| Cím: | Térbe kilépő bizonyítások VII. | |
| Szerző(k): | Kós Géza | |
| Füzet: | 2020/április, 194 - 201. oldal |  PDF | MathML PDF | MathML |
|
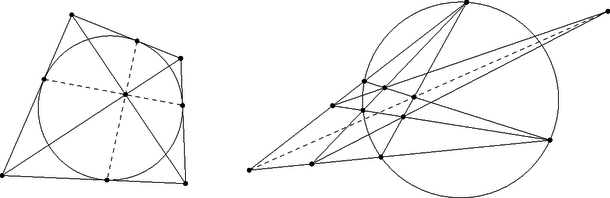
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Ebben a cikksorozatban olyan bizonyításokat mutatunk be, amikor a geometriai alakzatokat ,,térbe kilépve'', három- vagy akár még magasabb dimenziós objektumok vetületeként vagy metszeteként állítjuk elő. A polaritások olyan kölcsönösen egyértelmű megfeleltetések, amelyek a projektív sík pontjait a projektív sík egyeneseivel párosítják össze úgy, hogy bármely egyenesre és pontra igaz, hogy az akkor és csak akkor megy át -n, ha az -nek megfelelő pont illeszkedik a -hez rendelt egyenesre. A ponthoz rendelt egyenes a polárisa, és a egyeneshez rendelt pont a pólusa. Praktikus dolog az egymásnak megfeleltetett objektumokat ugyanazzal a betűvel jelölni, a pontokat nagy-, az egyeneseket kisbetűvel.1 Most a polaritás legismertebb, középiskolás versenyfeladatokban is gyakran előforduló speciális esetével, a körre vonatkozó polaritással fogunk foglalkozni. 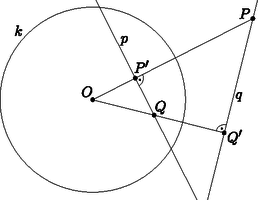 1. ábra Legyen egy rögzített kör, ez lesz a polaritás alapköre; a középpontja , sugara . A -ra vonatkozó polaritást fogjuk definiálni. Két lehetséges definíciót is szeretnék mutatni. Az első egy intuitív mód, ahogy az ember először maga fedezné fel a polaritás alaptulajdonságait, cserébe több technikai részletkérdést később kell végiggondolnunk. A második egy technikailag egyszerűbb, kompaktabb definíció, cserébe a geometriai tulajdonságokat kell külön ellenőrizni. Mindkét definíció lépéseit követhetjük az 1. ábrán. 1. definíció
2. definíció
Tetszés szerint, tekinthetjük az ‐. tulajdonságokat definíciónak és a ‐. tulajdonságokat következményeknek, vagy fordítva. A polaritás néhány további alaptulajdonsága:
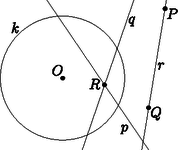 2a. ábra 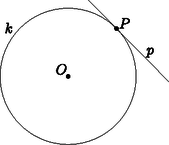 2b. ábra 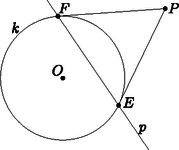 2c. ábra Az Olvasóra bízzuk annak végiggondolását, hogy a kétféle definíció ugyanazt a megfeleltetést írja le, és a fenti tulajdonságok is teljesülnek. Ha a síkot kiegészítjük a szokásos végtelen távoli pontokkal és az azokat tartalmazó ideális egyenessel, akkor definiálhatjuk az pont polárisát és az -n átmenő egyenesek pólusait is. Ha egy ideális pont, akkor polárisa az -n átmenő, az irányra merőleges egyenes. Ez szemléletesen megfelel annak, hogy ha a pontot valamelyik irányban végtelen messzire elmozgatjuk, akkor a polárisa is párhuzamosan mozog az pontra illeszkedő helyzetig. A 7. tulajdonság is érvényes marad; a határhelyzetben a -ből húzott érintők párhuzamosak az iránnyal (3. ábra). 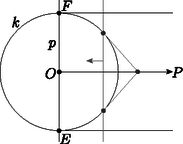 3. ábra Végül az pont polárisa az ideális egyenes; ezt is szemléltethetjük úgy, hogy a pontot az -ba húzzuk, miközben polárisa egyre távolabbra vándorol. 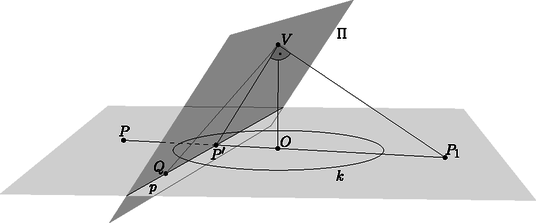 Mivel , az háromszög hasonló az háromszöghöz, emiatt . A egyenes merőleges -re és -re, ezért merőleges az síkra és az abban fekvő egyenesre is. A síkban most már két egyenesről, -ről és -ről is tudjuk, hogy merőleges -re, tehát a sík merőleges a egyenesre. Ez az észrevétel egy térbeli eljárást ad a pont polárisának szerkesztésére: tükrözzük -t -ra, így megkapjuk a pontot. A -ponton át, -re merőlegesen vegyük fel a síkot; a kimetszi az alapsíkból a egyenest. Azt is láthatjuk, hogy bármely pont akkor és csak akkor konjugált -vel, ha . Ha valamelyik ideális pont, akkor , az irány párhuzamos az alapsíkkal, és kimetszi az -n átmenő, -re merőleges egyenest. Ha pedig , akkor párhuzamos síkjával, a két sík metszete valóban az alapsík ideális egyenese. Tehát a fenti szerkesztés egységesen működik a projektív sík bármely pontjára. Ha van egy projektív geometriai állítás, tétel, amelyben pontok, egyenesek és (legfeljebb) egy kör szerepel, az ábrára alkalmazhatjuk a körre vonatkozó polaritást: minden pontot kicserélünk a polárisára, és minden egyenest kicserélünk a pólusára. Ilyen módon a projektív geometriai tételeket párokba állíthatjuk; mindegyik tételnek van egy párja, duálisa. Próbáljuk ki ezt az első részben látott Brianchon-tétellel: Brianchon tétele: Ha az , , , , , egyenesek érintik a kört, metszéspontjaik , , , , és , akkor a , és egyenesek egy ponton mennek át (5 ábra). 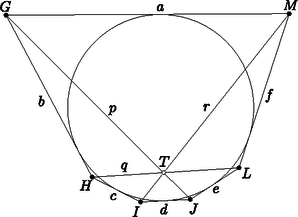 5. ábra 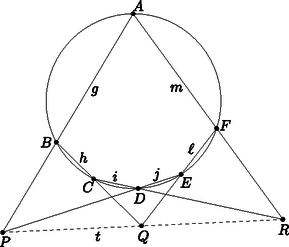 5. ábra A polaritást alkalmazva kapjuk a Pascal-tételt: Pascal2 tétele: Ha az , , , , , pontok egy körön vannak, az összekötő egyeneseik , , , , és , akkor ezek metszéspontjai, a , és pontok egy egyenesen vannak (5 ábra). A Brianchon-tétel és a Pascal-tétel egymás duálisa. Legyen az középpontú, az alapkörre illeszkedő gömb, és vegyünk fel két pontot, -t és -t a síkban, a körön kívül; a -ből -hoz húzott érintők végpontjai legyenek és . A 7. tulajdonság szerint a egyenes a pont polárisa. A egyenesre a mentén állítsunk egy merőleges síkot; ez a -t egy körben metszi; az merőleges a és szakaszokra. Ha rajta van a egyenesen, vagyis és konjugáltak, akkor a pont is az kör síkjában van, a körön kívül. Húzzuk meg -ból az egyik érintőjét; az érintési pontot jelöljük -vel. Vegyük észre, hogy a és a szakasz is érintője -nek, ezért a sík érinti a gömböt. Továbbá a szakasz a elforgatottja, szintén merőleges -re és a körhöz húzott érintőre, tehát a és szakaszok merőlegesek (6. ábra). 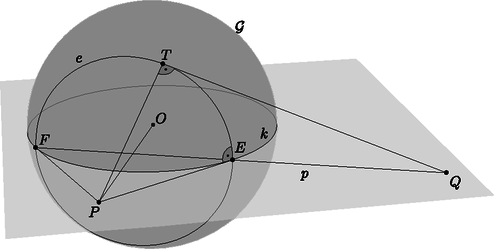 Végig lehet gondolni, hogy ezek a lépések megfordíthatók: ha egy, a és pontokon keresztül fektetett sík a pontban érinti a gömböt úgy, hogy és merőlegesek, akkor a egyenesre esik, vagyis és konjugáltak. Melléktermékként a 4. tulajdonságra is egy új bizonyítást adtunk, legalábbis külső pontok esetén. Azokat a háromszögeket, amelyekben mindegyik csúcs a vele szemközti oldal pólusa, autopoláris háromszögnek hívjuk, de van, aki a görög‐angol autopolar név betű szerinti átírását szereti. Bármely két konjugált , pont kiegészíthető autopoláris háromszöggé, a harmadik, csúcs a egyenes pólusa, amely -vel és -val is konjugált. Például a ponttal és is konjugált, ezért polárisa csak a egyenes lehet. Az autopoláris háromszögeknek egy nagyon fontos előfordulása, versenyfeladatok megoldásában is gyakran találkozhatunk vele, amikor egy húrnégyszög szemközti oldalpárjainak és átlóinak metszéspontját vesszük: Tétel. Ha , , és négy különböző pont a körön, és metszéspontja , és metszéspontja , továbbá és metszéspontja , akkor a háromszög -ra nézve autopoláris. A háromszög magasságpontja a középpontja (7. ábra). A tétel része triviálisan következik az állításból: ha autopoláris háromszög, akkor például a egyenes a pont polárisa, ami az tulajdonság miatt merőleges az egyenesre, tehát a háromszögben a oldalhoz tartozó magasságvonal. Ugyanez a másik két oldalra is elmondható, tehát a három magasságvonal metszéspontja. Az részt a térbe kilépve fogjuk igazolni. Az , , , pontok szerepe szimmetrikus; feltehetjük, hogy egy konvex húrnégyszög, így és a körön kívül, pedig a körön belül helyezkedik el. 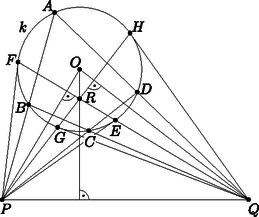 7. ábra 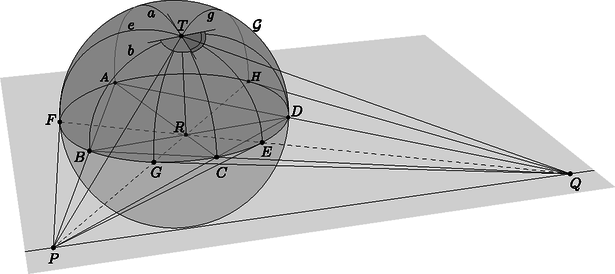 A középpontú, sugarú inverzió a gömböt önmagára képezi, felcseréli egymással -t -vel, valamint -t -vel, ezért az alapsíkra merőleges és köröket is egymásra képezi. A egyenesen a két kör egyetlen ‐ közös ‐ pontja, tehát az inverziónak ‐ és mellett ‐ is fixpontja, tehát érinti -t. Az ilyen pontok az alapsíkra merőleges, átmérőjű körön vannak, tehát az sík is merőleges síkjára, így tartalmazza a szakaszt és vele együtt az pontot. Ebből azt is látjuk, hogy az egyenes átmegy az ponton. De az egyenes a pont polárisa, tehát és konjugáltak. Ugyanígy láthatjuk, hogy és konjugáltak. Az előbbi, középpontú inverzió önmagára képezi a egyenest és felcseréli egymással az és köröket; az inverzió szögtartása miatt a egyenes ugyanakkora szöget zár be a két körrel, illetve a pontban húzott érintőikkel. Mindhárom egyenes egy síkban, a -ben a gömbhöz fektetett érintősíkban van; tehát a két kör közötti egyik szög felezője. Hasonlóan, a egyenes a két kör közötti másik, kiegészítő szög felezője. A két szögfelező, vagyis és merőlegesek, tehát és konjugáltak. Ezzel beláttuk, hogy a pontok páronként konjugáltak, vagyis a háromszög valóban autopoláris.
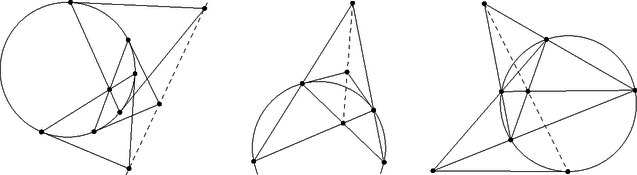 
1A cikksorozat a Rényi Intézet és a Sztaki támogatásával készült.2Blaise Pascal (1623‐1662) francia matematikus és filozófus |