Cím:	Gyakorló feladatsor emelt szintű matematika érettségire
Szerző(k):	Szoldatics József (Budapest)
Füzet:	2020/március, 146 - 148. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Oldjuk meg a valós számok halmazán a következő egyenletet: $\begin{array}{c}{\displaystyle x^2-14=2\sqrt[]{x^2+1}\mathrm{.}}\end{array}$ (6 pont) $b)$ Oldjuk meg a valós számok halmazán a következő egyenletrendszert: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{2x^{2}y}{2x^2+y}}& {\displaystyle =\frac{1}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{12x^{2}y}{4x^2+3y}}& {\displaystyle =\frac{1}{5}\mathrm{.}}\hfill \end{array}}$     (7 pont)     2. $a)$ Oldjuk meg a valós számok halmazán a következő egyenletet: $\begin{array}{c}{\displaystyle 4^x+4\cdot 2^{-x}=5.}\end{array}$ (6 pont) $b)$ Oldjuk meg a valós számok halmazán a következő egyenletet: $\begin{array}{c}{\displaystyle \text{sin}{}^{6}x+\text{cos}{}^{6}x=-2+3\text{cos}2x\mathrm{.}}\end{array}$ (7 pont)   3. $a)$ Oldjuk meg a valós számok halmazán a következő egyenletet: $\begin{array}{c}{\displaystyle 1+\frac{3}{\text{log}{}_4\left(x^2-6x+13\right)}=\frac{4}{\text{log}{}_2\left(x+1\right)}+\frac{\text{log}{}_2{\left(x+1\right)}^2}{2}\mathrm{.}}\end{array}$ (8 pont) $b)$ Egy szabályos dobókockát hatvanszor feldobva 15 esetben kaptunk hatost. Ezt a kísérletet egymás után többször elvégezve mindig ehhez hasonló eredményre jutunk. Emiatt úgy sejtjük, hogy a dobókocka ,,cinkelt'', azaz a hatos megnövelt valószínűséggel bír. Mekkora ez a valószínűség, ha minden 60-as sorozat esetén 15 lett a kapott érték (azaz várható érték 15)?  (4 pont)   4. $a)$ Egy nem állandó számtani sorozat első, második és negyedik eleméhez rendre 1-et adunk, így egy mértani sorozat második, harmadik és negyedik elemét kapjuk. A mértani sorozat első, második és harmadik elemének az összege 7. Mennyi a számtani sorozat 1010-edik eleme?  (6 pont) $b)$ Adott a következő sorozat: $\begin{array}{c}{\displaystyle a_1=1;a_{n+1}=3\cdot a_n+1\left(n\ge 1\right)\mathrm{.}}\end{array}$ Adjuk meg a sorozat 2020-adik tagját.  (7 pont)   II. rész     5. $a)$ Legyen $a$ és $b$ nemnegatív valós szám. Bizonyítsuk be, hogy $\begin{array}{c}{\displaystyle 0\le \frac{\left(a+1\right)\left(b+1\right)}{a^2+b^2+2}\le 1.}\end{array}$ Írhatunk-e a nulla helyett nála nagyobb számot?  (9 pont) $b)$ Egy felül nyitott fémdobozt lemezből állítunk elő úgy, hogy az 1. ábrán látható módon kivágunk, majd összehajtogatunk egy ilyen alakot. 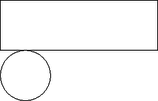    1. ábra   A kivágást egy 30 cm-es széles fémszalagból végezzük úgy, hogy 2 ilyen mintát fordítunk egymással szembe a 2. ábra szerint. 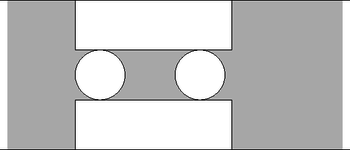    2. ábra   Hogyan válasszuk meg a méreteket, hogy a kikerülő fémdoboz a lehető legnagyobb térfogatú legyen?  (7 pont)   6. $a)$ Adjuk meg annak az egyenesnek az egyenletét, mely egyidejűleg érintik az $y=x^2$ és $y=-x^2+4x-2$ parabolákat.  (9 pont) $b)$ A magyar GúgLi Kft. egy emblémát tervez a székházuk elé, amely egy félbevágott gömb és egy kúp összetételéből áll. Az emblémának függőlegesen a negyede ki van vágva úgy, hogy a két vágósík az embléma függőleges tengelye mentén metszi egymást. Az embléma keresztmetszete és a függőleges metszete az ábrán látható. 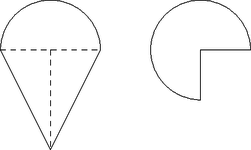    A kúp magassága éppen a félbevágott gömb sugarának a kétszerese. Betonból szeretnék elkészíttetni majd lefesteni a 1,5 m magasságúra tervezett emblémát. ‐ Mennyi beton szükséges az elkészítéséhez, ha az elkészítés folyamán 15% veszteséggel számolhatunk? ‐ Mekkora lesz az elkészült embléma tömege? ‐ Hány $m^2$-re elegendő festéket kell beszerezniük, ha az időjárás ellen háromszor szeretnék lefesteni és a festés során keletkező veszteség 5%?  (7 pont)   7. $a)$ 18 tudós e-mail segítségével tartja a kapcsolatot a világban. Bármely két tudós egymással angol, német vagy orosz nyelven levelezik, mindig ugyanazt a nyelvet használják egymás között. Tudjuk, hogy nincs három olyan tudós, aki egymás között angol, vagy orosz nyelvet használ. Bizonyítsuk be, hogy létezik közöttük három, akik egymással németül leveleznek.  (9 pont) $b)$ Aladár négyjegyű számokat ír fel egy papírlapra, melyek csak az 1; 2; 3 és 4 számjegyeket tartalmazhatják (lehet ismétlődés, nem kell minden számjegyet felhasználni minden négyjegyű számban). Figyel arra, hogy 1-es után csak 4-es, páros számjegy után csak páratlan jegy következhet. Hányféle számot tud leírni így?  (7 pont)   8. $a)$ Oldjuk meg a következő egyenletet a pozitív egészek halmazán: $\begin{array}{c}{\displaystyle 2\cdot \left(x;y\right)+17\cdot \left[x;y\right]=\mathrm{257,}}\end{array}$ ahol a ,,kerek" zárójel a két szám legnagyobb közös osztóját, a ,,szögletes" zárójel pedig a legkisebb közös többszörösét jelöli.  (9 pont) $b)$ Egy szimmetrikus trapéz párhuzamos oldalai 2 és 14, szárai 10 egység hosszúak. Meghúzzuk a belső szögeinek szögfelezőjét, amelyek egy négyszöget zárnak be. Amennyiben ennek a négyszögnek létezik a beírt és körülírt köre, mekkora ezen körök sugara?  (7 pont)   9. $a)$ Bizonyítsuk be, hogy ${\displaystyle \begin{array}{c}\hfill {\displaystyle 1\cdot 2+2\cdot 3+\text{...}+n\cdot \left(n+1\right)=}\hfill \\ \hfill {\displaystyle =\frac{n\cdot \left(n+1\right)\cdot \left(n+2\right)}{3}\mathrm{,}}\hfill \end{array}}$ ahol $n\in {\text{N}}^{+}$.  (8 pont) $b)$ Adott egy olyan húrnégyszög, ami egyben érintőnégyszög is. 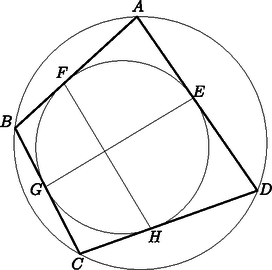    Az ábrán jelöltük az érintési pontokat. Bizonyítsuk be, hogy az $EG$ és $FH$ szakaszok merőlegesek egymásra.   (8 pont)