⁰
A KöMaL egy régi száma pontverseny kívüli problémaként közölte a Knaster‐Tarski-féle fixponttételt. Cikkünkben elsőként fölidézzük a problémát, majd bemutatjuk egyik legfontosabb, halmazelmélethez kötődő alkalmazását. Ezáltal egyben bepillantást kívánunk adni a számosságaritmetika lenyűgözően szép, meglepetésekkel teli világába is.

 

Megoldás. Álljon a $\text{H}$ halmazcsalád azokból a $H\subseteq X$ halmazokból, melyekre $F\left(H\right)\subseteq H$. Ez a $\text{H}$ család nem üres, mert $X$ eleme, hiszen $F\left(X\right)\subseteq X$ biztosan teljesül. Legyen a $\text{H}$-beli halmazok közös része $H_0$. Mit tudunk az $F\left(H_0\right)$ halmazról?
Ha $H$ tetszőleges $\text{H}$-beli halmaz, akkor $H_0\subseteq H$ miatt fönnáll, hogy $F\left(H_0\right)\subseteq F\left(H\right)$. Ebből pedig $F\left(H\right)\subseteq H$ alapján (ez volt a $\text{H}$-beli halmazok definiáló tulajdonsága) $F\left(H_0\right)\subseteq H$ következik. Tehát az $F\left(H_0\right)$ halmazt minden $\text{H}$-beli halmaz tartalmazza, így metszetük, $H_0$ is: $F\left(H_0\right)\subseteq H_0$. Ugyanakkor $F\left(H_0\right)\subseteq H_0$-ból $F\left(F\left(H_0\right)\right)\subseteq F\left(H_0\right)$ adódik, tehát (definíció szerint) az $F\left(H_0\right)$ halmaz $\text{H}$-beli. A $H_0$ minden $\text{H}$-beli halmaznak része, így $H_0\subseteq F\left(H_0\right)$. Ezt az előbbi $F\left(H_0\right)\subseteq H_0$ eredményünkkel összevetve $F\left(H_0\right)=H_0$, ami azt jelenti, hogy a keresett részhalmazt megtaláltuk.  $\square$

 

Adott $X$ halmaz esetén jelölje $\text{P}\left(X\right)$ az $X$ összes részhalmazainak halmazát, másképpen mondva: hatványhalmazát. Azt mondjuk, hogy az $F:\text{P}\left(X\right)\to \text{P}\left(X\right)$ leképezés monoton, ha megőrzi a tartalmazást, vagyis $A\subseteq B\subseteq X$ esetén $F\left(A\right)\subseteq F\left(B\right)$ is teljesül. Az $F$ leképezésnek $H\subseteq X$ fixpontja, ha $F\left(H\right)=H$. Ezekkel az elnevezésekkel a P. 329 probléma tömören így is megfogalmazható:

 

Tétel. Adott hatványhalmaz bármely monoton leképezésének létezik fixpontja.

 

Ez az állítás először a Lengyel Matematikai Társulat Varsói Részlegének ülésén hangzott el 1927-ben, és azóta Knaster‐Tarski-féle fixponttételként szokás hivatkozni [1]. Később, az eredetileg Knaster által előadott eredményt Tarski [3] fejlesztette tovább, számos meglepő és hatékony alkalmazást adva a halmazelmélet, logika, absztrakt algebra és valós függvénytan terén. Manapság úgy tekintünk Knaster és Tarski eredményére, mint a monoton leképezések fixpontelméletének első zsengéjére.
A Knaster‐Tarski-féle fixponttételnek már az eredeti változata is jelentős alkalmazásokkal bír. Az egyik legfontosabb a számosságaritmetika terén Schröder‐Bernstein-tételként ismert állítás. Fő célunk ezt, és ennek néhány következményét bemutatni, és egyúttal rövid barangolást tenni a számosságok meglepő és izgalmas birodalmába.

 

2. A számosságaritmetika alapjai

Azt mondjuk, hogy két halmaz egyenlő számosságú, vagy másképpen: ekvivalens, ha létezik közöttük egy bijekció, azaz kölcsönösen egyértelmű leképezés. Ha $A$ és $B$ ekvivalens halmazok, akkor ezt az $A\sim B$ módon jelöljük. A halmazok ekvivalenciája egyfajta ,,számolás'' számfogalom nélkül. Birtokában nemcsak a halmazok elemszám szerinti egyenlőségét értelmezhetjük, hanem a végtelen halmaz fogalmát is bevezethetjük. Egy halmaz végtelen, ha létezik önmagával ekvivalens valódi részhalmaza. Eszerint a pozitív egészek $\text{N}$ halmaza végtelen, hiszen a $\phi \left(n\right)=n+1$ módon értelmezett leképezés bijektíven hat $\text{N}$ és $\text{N}\setminus \left\{1\right\}$ között. A pozitív egészek halmazával ekvivalens halmazok a megszámlálhatóan végtelen halmazok. Igen egyszerűen nyerjük például, hogy az egész számok $\text{Z}$ halmaza megszámlálhatóan végtelen. Ehhez elegendő csupán a

$\begin{array}{c}{\displaystyle \phi \left(k\right):=\{{\displaystyle \begin{array}{cc}\hfill {\displaystyle 2\left(k-1\right)\mathrm{,}}& {\displaystyle \text{ha }k\in \text{N}\mathrm{,}}\hfill \\ \hfill {\displaystyle 1-2k\mathrm{,}}& {\displaystyle \text{ha }k\in \text{Z}\setminus \text{N}}\hfill \end{array}}}\end{array}$

módon értelmezett, $\phi :\text{Z}\to \text{N}$ bijektív leképezést tekinteni. Tehát a $\text{Z}\sim \text{N}$ állítás közvetlenül, definíció szerint igazolható.
Az ekvivalencia közvetlen ellenőrzése azonban általában nehéz, így egy hatékonyabb módszer kidolgozása szükséges. Ehhez elsőként bevezetjük az injektív leképezés fogalmát. A $\phi :A\to B$ leképezés injektív, ha $\phi \left(a\right)=\phi \left(a^{*}\right)$ esetén $a=a^{*}$ következik. Ha létezik ilyen injektív leképezés, akkor az $A$ halmazt kisebb vagy egyenlő számosságúnak nevezzük a $B$ halmaznál. Ezt jelölésben az $A⪯B$ módon fejezzük ki.
Nyilvánvalóan minden bijekció inverzével együtt injektív, tehát ha két halmaz ekvivalens, akkor bármelyik kisebb vagy egyenlő számosságú a másiknál. Jelölésekkel élve, ha $A\sim B$, akkor $A⪯B$ és $B⪯A$ teljesül. Ennek az észrevételnek a megfordítása is érvényes, amelyet a Schröder‐Bernstein-tétel fogalmaz meg. Az állítás leképezések nyelvén így szól: Ha egy halmaz injektíven képezhető egy másikba és a másik az egyikbe, akkor létezik köztük bijekció is. A bizonyítás a Knaster‐Tarski-féle fixponttételre támaszkodik. Mielőtt a részletekre térnénk, szükségünk lesz a következőkre. Ha a $H$ részhalmaza egy $X$ alaphalmaznak, és $f:X\to X$ egy függvény, akkor a $H$ halmaz $f$ általi képét a szokásos $f\left(H\right):=\left\{f\left(x\right)\mid x\in H\right\}$ módon értelmezzük. Az értelmezésből következik, hogy $A\subseteq B$ esetén $f\left(A\right)\subseteq f\left(B\right)$ is fennáll. Másképpen fogalmazva, az $F_f\left(H\right):=f\left(H\right)$ előírással adott $F_f:\text{P}\left(X\right)\to \text{P}\left(X\right)$ leképezés monoton.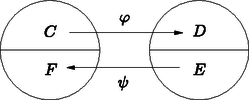

 

Tétel. Ha $A⪯B$ és $B⪯A$, akkor $A\sim B$.

 

Bizonyítás. Az $A⪯B$ és $B⪯A$ feltételek miatt léteznek $\phi :A\to B$ és $\psi :B\to A$ injektív függvények. Célunk annak igazolása, hogy ekkor bijekció is létezik a két halmaz között. Ehhez az $A$ és $B$ halmazokat fogjuk alkalmas módon két-két diszjunkt részre bontani $\phi$ és $\psi$ segítségével:

 

 

 

Legyen $C\subseteq A$ tetszőleges, és tekintsük a $D:=\phi \left(C\right)$ halmazt. Ekkor nyilván $\phi$ bijektíven hat $C$ és $D$ között. Legyen most $E:=B\setminus D$, valamint $F:=\psi \left(E\right)$. Világos, hogy ekkor $\psi$ bijektív $E$ és $F$ között. Ha még ráadásul az is kiderülne, hogy $C$ és $F$ diszjunktak és az uniójuk $A$, akkor az

$\begin{array}{c}{\displaystyle f\left(x\right):=\{{\displaystyle \begin{array}{cc}\hfill {\displaystyle \phi \left(x\right)\mathrm{,}}& {\displaystyle \text{ha }x\in C\mathrm{,}}\hfill \\ \hfill {\displaystyle {\psi }^{-1}\left(x\right)\mathrm{,}}& {\displaystyle \text{ha }x\in F}\hfill \end{array}}}\end{array}$

módon adott $f:A\to B$ függvény jóldefiniált és bijektív. Kérdés tehát, hogy létezik-e ilyen választás $C$-re. Az $E$, $F$, $D$ halmazok értelmezését szem előtt tartva tehát azt várjuk el, hogy

$\begin{array}{c}{\displaystyle C\underset{}{\overset{\text{?}}{=}}A\setminus F=A\setminus \psi \left(E\right)=A\setminus \psi \left(B\setminus D\right)=A\setminus \psi \left(B\setminus \phi \left(C\right)\right)}\end{array}$

teljesüljön. Értelmezzük a $T:\text{P}\left(A\right)\to \text{P}\left(A\right)$ leképezést ez utóbbi taggal, azaz legyen $C\subseteq A$ esetén

$\begin{array}{c}{\displaystyle T\left(C\right):=A\setminus \psi \left(B\setminus \phi \left(C\right)\right)\mathrm{.}}\end{array}$

Egyszerűen meggyőződhetünk arról, hogy $T$ monoton leképezés. Ezért a Knaster‐Tarski fixponttétel értelmében valóban létezik olyan $C$, hogy $T\left(C\right)=C$.  $\square$

 

Ezt az állítást elsőként Cantor fogalmazta meg bizonyítás nélkül 1887-ben. Még ugyanebben az évben Dedekind elemi bizonyítást talált, amit nem publikált, sőt Cantort sem értesítette eredményéről. Később 1897-ben, az akkor 19 éves hallgató, Bernstein bemutatta bizonyítását Cantor egyetemi szemináriumán. Bernsteintől függetlenül, ugyancsak 1897-ben Schröder is közölte bizonyítását, amiről később kiderült, hogy hibás.
A Schröder‐Bernstein-tétel segítségével egyszerűen kapjuk, hogy a racionális számok $\text{Q}$ halmaza megszámlálhatóan végtelen. Elsőként azt érdemes megmutatni, hogy $\text{N}\times \text{N}\sim \text{N}$. Azonnal látható, hogy az $n\mapsto \left(n\mathrm{,}n\right)$ leképezés injektív, azaz $\text{N}⪯\text{N}\times \text{N}$. Elegendő tehát csupán egy $\phi :\text{N}\times \text{N}\to \text{N}$ injektív leképezést megadnunk. Legyen

$\begin{array}{c}{\displaystyle \phi \left(n\mathrm{,}m\right):=2^n\cdot 3^m\mathrm{.}}\end{array}$

Ha most $\phi \left(n\mathrm{,}m\right)=\phi \left(k\mathrm{,}l\right)$, akkor definíció szerint $2^n\cdot 3^m=2^k\cdot 3^l$; az egyértelmű prímfaktorizáció tétele miatt ebből $n=k$ és $m=l$ következik. Tehát $\left(n\mathrm{,}m\right)=\left(k\mathrm{,}l\right)$, ami pontosan $\phi$ injektivitását mutatja. Ennek mintájára az is igazolható, hogy $\text{Z}\times \text{N}\sim \text{N}$. Végezetül, a $\text{Q}\sim \text{N}$ állítás ebből már következik, hiszen minden racionális szám egyértelműen előáll egy, tovább már nem egyszerűsíthető egész és természetes szám hányadosaként.
Az $\text{N}\times \text{N}\sim \text{N}$ igazolása történhet a jól ismert ,,átlós bejárással'', ami közvetlenül bijekciót eredményez a szóban forgó halmazok között. Azonban végképp föl kell adnunk a közvetlen módszert, ha a $\left]\mathrm{0,1}\right[$ intervallum számosságát egy hatványhalmaz számosságával akarjuk kifejezni:

 

Tétel. $\text{P}\left(\text{N}\right)\sim \left]\mathrm{0,1}\right[$.

 

Bizonyítás. Elsőként azt igazoljuk, hogy létezik egy $\phi :\text{P}\left(\text{N}\right)\to \left]\mathrm{0,1}\right[$ injektív leképezés. Legyen $A\subset \text{N}$ tetszőleges, nemüres halmaz. Értelmezzük az $\left(a_n\right)$ sorozatot és ennek birtokában az $x$ valós számot az alábbiak szerint:

$\begin{array}{c}{\displaystyle a_n=\{{\displaystyle \begin{array}{cc}\hfill {\displaystyle \mathrm{0,}}& {\displaystyle \text{ha }n\notin A\mathrm{,}}\hfill \\ \hfill {\displaystyle \mathrm{1,}}& {\displaystyle \text{ha }n\in A;}\hfill \end{array}}\text{illetve}x=\mathrm{0,}{a}_1{a}_2{a}_3\text{...}}\end{array}$

Világos, hogy az $A$ halmaz egyértelműen meghatározza az $\left(a_n\right)$ sorozatot, e sorozat pedig az $x$ valós számot. Nyilvánvaló az is, hogy $x\in \left]\mathrm{0,1}\right[$. Legyen $\phi \left(A\right):=x$, s tegyük fel, hogy $\phi \left(B\right)=x$ szintén fennáll. Az $\left(a_n\right)$ definíciója miatt ez azt jelenti, hogy minden $n\in \text{N}$ esetén $n\in A$ pontosan akkor teljesül, ha $n\in B$. Így $A=B$, ami pedig a $\phi$ injektivitását adja. Ha $A=\varnothing$, akkor legyen $\phi \left(A\right):=0\mathrm{,}2$; ezzel a kiterjesztéssel $\phi$ továbbra is injektív.
Most azt igazoljuk, hogy létezik egy $\psi :\left]\mathrm{0,1}\right[\to \text{P}\left(\text{N}\right)$ injektív leképezés. Legyen $x\in \left]\mathrm{0,1}\right[$, s legyen $\left(x_n\right)$ az $x$ tizedesjegyeinek sorozata. Értelmezzük ekkor a $\psi \left(x\right)$ halmazt a

$\begin{array}{c}{\displaystyle \psi \left(x\right)=\left\{10\left(n-1\right)+x_n+1\mid n\in \text{N}\right\}}\end{array}$

előírással. Nyilván $\psi \left(x\right)\subseteq \text{N}$, tehát $\psi :\left]\mathrm{0,1}\right[\to \text{P}\left(\text{N}\right)$. Legyen $y\in \left]\mathrm{0,1}\right[$, jelölje $\left(y_n\right)$ az $y$ tizedesjegyeinek sorozatát. Ekkor a $\psi \left(y\right)$ halmaz

$\begin{array}{c}{\displaystyle \psi \left(y\right)=\left\{10\left(m-1\right)+y_m+1\mid m\in \text{N}\right\}}\end{array}$

alakú. Tegyük fel, hogy $\psi \left(x\right)=\psi \left(y\right)$. Két halmaz pontosan akkor egyenlő, ha elemei ugyanazok, így minden $n\in \text{N}$ esetén található olyan $m\in \text{N}$, hogy

$\begin{array}{c}{\displaystyle 10\left(n-1\right)+x_n+1=10\left(m-1\right)+y_m+1.}\end{array}$

Ha itt $n<m$ teljesül, akkor $n\le m-1$ is fönnáll. Fölhasználva azt is, hogy $x_n\le 9$ és $y_m\ge 0$, kapjuk, hogy

${\displaystyle \begin{array}{cc}\hfill {\displaystyle 10\left(n-1\right)+x_n+1}& {\displaystyle \le 10\left(m-2\right)+x_n+\mathrm{1,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle =10\left(m-1\right)+x_n-\mathrm{9,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle \le 10\left(m-1\right)<10\left(m-1\right)+y_m+\mathrm{1,}}\hfill \end{array}}$

ami ellentmondás. Az $m<n$ eset ugyanígy kizárható. Tehát $m=n$, amiből pedig $x_n=y_n$ következik. Ez azt mutatja, hogy $x$ és $y$ tizedestört alakja azonos. Mivel a tizedestört alak egyértelmű, ezért $x=y$. Vagyis $\psi$ injektív.
Az eddigieket összefoglalva megállapíthatjuk, hogy $\text{P}\left(\text{N}\right)⪯\left]\mathrm{0,1}\right[$ és $\left]\mathrm{0,1}\right[⪯\text{P}\left(\text{N}\right)$ egyszerre teljesülnek. Így a Schröder‐Bernstein-tétel fényében $\left]\mathrm{0,1}\right[\sim \sim \text{P}\left(\text{N}\right)$ is fönnáll.  $\square$

 

Világos, hogy a $\left]\mathrm{0,1}\right[$ intervallum, s ennélfogva $\text{P}\left(\text{N}\right)$ is végtelen halmaz. Fölmerül a kérdés, hogy ez a közös számosság milyen kapcsolatban áll a megszámlálhatóan végtelennel. Cantor alábbi tétele ennél sokkal általánosabb kérdést válaszol meg: a hatványhalmaz számossága mindig szigorúan nagyobb a halmaz számosságánál.

 

Tétel. $A\prec \text{P}\left(A\right)$.

 

Bizonyítás. Ha $A=\varnothing$, akkor az állítás nyilvánvaló, hiszen ekkor $\text{P}\left(A\right)=\left\{\varnothing \right\}$ nem üres. Föltehető, hogy $A$ nem üres. Nyilván $\text{P}\left(A\right)$ egyelemű részhalmazai és $A$ elemei kölcsönösen egyértelműen megfelelnek egymásnak, tehát $A⪯\text{P}\left(A\right)$. Indirekt módon tegyük fel, hogy létezik egy $\phi :A\to \text{P}\left(A\right)$ bijekció. Legyen ekkor

$\begin{array}{c}{\displaystyle B=\left\{a\in A\mid a\notin \phi \left(a\right)\right\}\mathrm{.}}\end{array}$

Mivel $\phi$ bijektív, ezért van olyan $b\in A$, hogy $\phi \left(b\right)=B$. Ha most $b\in B$, akkor ez azt jelenti, hogy $b\notin \phi \left(b\right)$ teljesül. Azonban $\phi \left(b\right)=B$, ami ellentmondás. Ha $b\notin B$, akkor ebből $b\notin \phi \left(b\right)$, azaz $b\in B$ adódik, ami szintén ellentmondás.  $\square$

 

A $\text{P}\left(\text{N}\right)$ halmazzal ekvivalens halmazokat kontinuum számosságúnak nevezzük. Megmutatható, hogy bármely intervallum, az irracionális számok halmaza, vagy a valós számok halmaza kontinuum számosságú. Így, a számhalmazok körében a kontinuum a legnagyobb előforduló számosság, hiszen a föntiek szerint a kontinuum a megszámlálható végtelennél ,,nagyobb'' végtelen. Azonban Cantor tételéből ennél jóval több következik. Minden számosságnál létezik nagyobb számosság! Jogosan mondhatjuk tehát: ez azért már mégiscsak több a soknál $\text{...}$

 

Hivatkozások

[1]	B. Knaster and A. Tarski, Un théoreme sur lesfonctions d'ensembles, Ann. Soc. Polon. Math., 6 (1927), 133‐134.

[2]	P. Szegedy, Solution to problem P. 329, KöMaL, 61 (1980), no. 2, 75.

[3]	A. Tarski, A lattice-theoretical fixpoint theorem and its applications, Pacific J. Math., 5 (1955), 285‐309.