Cím:	Térbe kilépő bizonyítások VI.
Szerző(k):	Kós Géza
Füzet:	2020/március, 130 - 141. oldal	PDF  |  MathML
Témakör(ök):	Térgeometriai bizonyítások, Szakmai cikkek

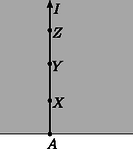
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Állandó távolságú görbepárok  Ebben a cikksorozatban olyan bizonyításokat mutatunk be, amikor a geometriai alakzatokat ,,térbe kilépve'', három- vagy akár még magasabb dimenziós objektumok vetületeként vagy metszeteként állítjuk elő.   Vasúti sínek és beírt körök     A Newcastle-i központi vasútállomás sínei egy 1910-es képeslapon   A vasúti sínpárokat jól ismerjük: két olyan görbéből állnak, amelyek távolsága egy előre rögzített $d$ állandó, a sínpár nyomtávja. Úgy is mondhatjuk, hogy a vasútvonal bármelyik pontján a két sín közé $d$ átmérőjű kört lehet írni.1     1. ábra   Ahol két sínpár keresztezi egymást, ott a kereszteződésben egy közelítőleg rombusz alakú terület jön létre, ezért az ilyen helyeket, az osztott pályás autóutak kereszteződéseihez hasonlóan, gyémánt-kereszteződésnek (angolul: diamond-crossing) is hívják. A kereszteződésben a két sínpár közé írt körseregeknek egy közös elemét fedezhetjük fel: a ,,rombuszba'' beírt kört, amely mind a négy síngörbét érinti (1. ábra). Látni fogjuk, hogy ebből a gondolatból milyen sokféle feladatot lehet gyártani; az előző részben látott olimpiai feladatjavaslatnak is van ilyen hangulatú megoldása. Ehhez most kivételesen nem három dimenzióba, hanem egy nem-euklideszi geometriai modellbe, a Poincaré-féle félsíkmodellbe fogunk átlépni, és ott keresünk állandó távolságú görbepárokat és ilyenek kereszteződéseit.   A Poincaré-féle félsíkmodell A félsíkmodell inverzióval kapható a Poincaré-féle körmodellből; szintén a hiperbolikus sík egy modellje, ha tetszik, egy képe az euklideszi síkon belül. A ,,pontok'' egy félsík belső pontjai. A modellt mindig úgy fogom lerajzolni, hogy a határa egy vízszintes egyenes, és az egyenes fölötti félsík lesz maga a modell. Az ,,egyenesek'' a félsík határára merőleges félkörök és félegyenesek. A félegyeneseket tekinthetjük a félkör határhelyzetének; ha a síkot kiegészítjük egy végtelen távoli ponttal, amely az összes egyenes közös végpontja (vagyis a modellt az inverzív síkon helyezzük el), ez az ideális pont lesz a félegyenesnek látszó ,,egyenesek'' másik vége. Máris látjuk, hogy a különféle geometriai alakzatok és mennyiségek a modellen belül nem ugyanazok, mint aminek kívülről látszanak. A hiperbolikus ,,sík'' félsíknak látszik, az ,,egyenesek'' pedig félkörnek vagy félegyenesnek. Azért, hogy a félreérthetőséget elkerüljük, a modellbeli dolgokat a későbbiekben is idézőjelbe fogom tenni, és helyenként a ,,hiperbolikus'' jelzőt is használni fogom. A kívülről látható dolgok nem lesznek idézőjelben, és időnként a ,,látszólagos'' jelzővel is hangsúlyozni fogom, hogy csak látszatról van szó. Két ,,pont'' ,,távolságát'' ugyanazzal a képlettel definiáljuk, mint a körmodellben: ha $X$ és $Y$ két pont a határegyenesre merőleges $AB$ félkörön (2.a ábra), akkor a ,,távolságuk'' $\begin{array}{c}{\displaystyle d\left(X\mathrm{,}Y\right)=k\cdot |\text{ln}\left(ABXY\right)|=k\cdot \left|\text{ln}\frac{AX\cdot YB}{AY\cdot XB}\right|\mathrm{,}}\end{array}$ ($1a$) ahol $k$ egy rögzített pozitív szám, a hiperbolikus geometria paramétere.     2. a ábra   Ha $X$ és $Y$ az $A$ végpontú, a határra merőleges félegyenesen van (2.b ábra), akkor a félegyenes másik vége az $I$ ideális pont, és $\frac{YI}{XI}=1$; tehát a ,,távolság'' $\begin{array}{c}{\displaystyle d\left(X\mathrm{,}Y\right)=k\cdot |\text{ln}\left(AIXY\right)|=k\cdot \left|\text{ln}\frac{AX}{AY}\right|\mathrm{.}}\end{array}$ ($1b$)     2. b ábra   A képletekben a logaritmus előjele attól függ, hogy a négy pont sorrendje $A$, $X$, $Y$, $B$ (a logaritmus értéke negatív) vagy pedig $A$, $Y$, $X$, $B$ (pozitív); ahol lehet, megpróbáljuk a pontokat úgy elhelyezni, hogy ne legyen szükség az abszolútérték-jelre. Érdemes ellenőrizni, hogy ez a távolság-képlet szimmetrikus, vagyis $d\left(X\mathrm{,}Y\right)=d\left(Y\mathrm{,}X\right)$, és additív is: ha $X$, $Y$, $Z$ ebben a sorrendben három pont ugyanazon az ,,egyenesen'', akkor $d\left(X\mathrm{,}Y\right)+d\left(Y\mathrm{,}Z\right)=d\left(X\mathrm{,}Z\right)$.   Végül definiáljuk a szögeket: két ,,egyenes'' ,,szöge'' a félsíkmodellben is éppen akkora, mint amekkorának látszik.   Körök és sugaraik A félsíkmodellben a ,,körök'' a félsík belsejében fekvő körvonalak, ezt most ellenőrizni fogjuk. Vizsgáljunk meg egy tetszőleges $k$ kört a félsíkban, amely szimmetrikus a határra merőleges $f$ félegyenesre; az $f$ kezdőpontját jelöljük $A$-val, és a $k$-val vett metszéspontjai legyenek $U$ és $V$. A kör látszólagos középpontja az $UV$ szakasz $F$ felezőpontja, de a kör ,,középpontja'' nem ez, hanem az $UV$ szakasznak az a $K$ pontja, amelyre $d\left(U\mathrm{,}K\right)=d\left(K\mathrm{,}V\right)$; az (1b) definíciót beírva $\frac{AK}{AU}=\frac{AV}{AK}$, vagyis $A{K}^2=AU\cdot AV$. Rajzoljunk a $K$ ponton keresztül egy tetszőleges újabb $e$ ,,egyenest'', vagyis félkört, amelynek végpontjai $B$ és $C$, metszéspontjai a $k$ körrel $X$ és $Y$ a 3. ábra szerint. 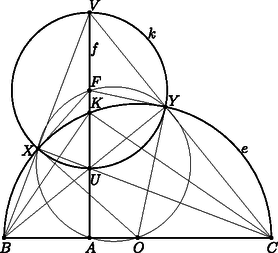    3. ábra   Azt szeretnénk ellenőrizni, hogy $e$ merőlegesen metszi $k$-t, és az $U$, $V$, $X$, $Y$ pontok ugyanakkora ,,távolságban'' vannak a $K$ ponttól, azaz $d\left(K\mathrm{,}U\right)=d\left(K\mathrm{,}V\right)=d\left(K\mathrm{,}X\right)=d\left(K\mathrm{,}Y\right)$. Azt már biztosítottuk, hogy $d\left(K\mathrm{,}U\right)=d\left(K\mathrm{,}V\right)$ teljesüljön. Először megmutatjuk, hogy a $BV$ és a $CU$ egyenes átmegy az $X$, míg a $BU$ és a $CV$ egyenes átmegy az $Y$ ponton. A Thalész-tétel miatt a $BCK$ háromszög derékszögű; a magasságtétel szerint $AB\cdot AC=A{K}^2$. A $K$ pont definíciója szerint $A{K}^2=AU\cdot AV$, tehát $AB\cdot AC=AU\cdot AV$, vagy átrendezve $\frac{AB}{AV}=\frac{AU}{AC}$. Ezért az $AVB$ és $ACU$ derékszögű háromszögek hasonlók, és egy $A$ körüli, ${90}^{\circ }$-os szögű forgatva nyújtással vihetők át egymásba. A ${90}^{\circ }$-os forgatás miatt az átfogóik, a $BV$ és a $CU$ egyenesek merőlegesek. A Thalész-tétel megfordítása miatt a $BV$ és a $CU$ egyenesek metszéspontja a $k$ és $e$ körön is rajta van, vagyis ez a metszéspont éppen az $X$ pont. Ugyanígy láthatjuk, hogy a $BU$ és $CV$ egyenesek metszéspontja $Y$. A $BCV$ háromszögben $BY$, $CX$ és $VA$ a magasságok, $U$ a magasságpont. Jelölje $O$ a $BC$ szakasz felezőpontját, amely egyben az $e$ kör középpontja is. Az $A$, $O$, $X$, $Y$, $F$ pontok a háromszög Feuerbach-körén vannak; mivel $OAF\sphericalangle ={90}^{\circ }$, az $OF$ szakasz a Feuerbach-körnek átmérője; ezért $OXF\sphericalangle =OYF\sphericalangle ={90}^{\circ }$. Más szóval, a $k$ kör $FX$ és $FY$ sugarai merőlegesek az $e$ kör $OX$, illetve $OY$ sugaraira; a $k$ és az $e$ kör tényleg merőlegesen metszi egymást. A $d\left(K\mathrm{,}X\right)$ ellenőrzéséhez azt használjuk fel, hogy a $BCK$ háromszög hasonló a $BKA$, a $BCX$ pedig hasonló a $BVA$ háromszöghöz: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{BK\cdot XC}{BX\cdot KC}=\frac{BK}{KC}\cdot \frac{XC}{BX}=\frac{BA}{AK}\cdot \frac{AV}{BA}=\frac{AV}{AK};}\hfill \\ \hfill {\displaystyle d\left(K\mathrm{,}X\right)=k\cdot \text{ln}\frac{BK\cdot XC}{BX\cdot KC}=k\cdot \text{ln}\frac{AV}{AK}=d\left(K\mathrm{,}V\right)\mathrm{.}}\hfill \end{array}}$ A $B$, $C$ és $X$, $Y$ pontok szerepének felcserélésével ugyanígy igazolható, hogy $d\left(K\mathrm{,}Y\right)=d\left(K\mathrm{,}V\right)$.   Az $\left(1a\right)$, $\left(1b\right)$ távolság-definíciók következménye, hogy a körívnek vagy éppen szakasznak látszó ,,szakaszok'' hiperbolikus hossza csupán a modell határától mért távolságok arányától függ; ha a félsíkmodellt felnagyítjuk, vagy lekicsinyítjük, ugyanezt a modellt kapjuk vissza. A 4. ábrán újra lerajzoltam az előző részben már látott csempézést, de most a félsíkmodellben: a csempék olyan egybevágó szabályos ötszögek, amelyeknek mindegyik szöge derékszög, és a beírt körük is ,,ugyanakkora'', csak a határhoz közelebbi köröket arányosan kisebbnek kell rajzolnunk.     4. ábra     Állandó távolságú görbepárok a félsíkmodellben Ahogy ígértem, vonatsíneket fogunk keresni a félsíkmodellben. Koncentrikus körök 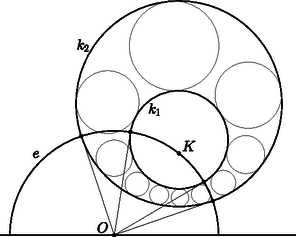  Az euklideszi geometriában megszokott párhuzamos egyenespárok itt nem léteznek; a legkézenfekvőbb példa állandó távolságú görbepárra két ,,koncentrikus'' ,,kör''. A ,,koncentrikust'' természetesen úgy értjük, hogy a két ,,kör'' hiperbolikus ,,középpontja'' ugyanaz. Az 5. ábrán a $k_1$ és a $k_2$ kör közös ,,középpontja'' a $K$ pont, és a mindkettőt érintő körök ,,ugyanakkorák''.     5. ábra   Tekintsünk egy tetszőleges, $K$-n átmenő $e$ ,,egyenest'', amely a modellben egy $O$ középpontú félkörnek látszik. Az $e$ ,,egyenes'' mindkét kört merőlegesen metszi, ezért az $O$ pontot a metszéspontokkal összekötő szakaszok érintik a köröket. Ezek a szakaszok az $e$ félkörnek sugarai, tehát egyenlő hosszúak; emiatt az $O$ pont hatványa a két körvonalra ugyanakkora. Ebből láthatjuk, hogy a ,,koncentrikus'' körök hatványvonala a félsíkmodell határegyenese.   Hiperciklusok Ha egy $e$ ,,egyenes'' két végét egy (a félkörtől különböző) $h$ körívvel összekötjük, egy nagyon érdekes görbét kapunk a hiperbolikus geometriánkban. Ennek a $h$ görbének minden pontja ugyanakkora ,,távolságban'' van az $e$-től. Ezért szokták a $h$ görbét ,,távolsággörbének'' is nevezni; mi az elterjedtebb ,,hiperciklus'' nevet fogjuk használni. Ha ugyanazzal a két végponttal nem egy, hanem két hiperciklust rajzolunk, akkor az $e$-től mért ,,távolságokat'' egyszerűen összeadhatjuk vagy kivonhatjuk (attól függően, hogy az $e$-nek ugyanazon vagy pedig ellentétes oldalán vannak), ezért a két hiperciklus ,,távolsága'' is állandó. A 6.a és a 6.b ábrán közös végpontú hiperciklusokat és ,,egyeneseket'' rajzoltam: a 6.b ábrán az egyik közös végpont az ideális pont. Vegyük észre, hogy a 6.a ábrán a hiperciklusoknak megfelelő körívek hatványvonala ezúttal is a félsíkmodell határa. 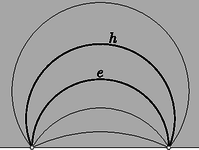    6. a ábra 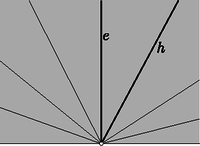      6. b ábra   A szakirodalom az egyeneseket, vagyis az egyenesektől nulla távolságban haladó görbéket nem nevezi ,,hiperciklusnak''. Mi viszont csupa olyan állítást fogunk megfogalmazni, amelyek hiperciklusokra és egyenesekre is érvényesek, ezért mindenhol azt kellene írnunk, hogy ,,hiperciklus vagy egyenes''. (Pl. ,,Két, közös végpontú hiperciklus vagy egyenes távolsága állandó''.) Helyette inkább a ,,hiperciklus'' fogalmába speciális esetként az egyeneseket is bele fogjuk érteni.   Most ellenőrizzük, hogy két, azonos végpontú hiperciklus (vagy ,,egyenes'') ,,távolsága'' tényleg állandó, és a közéjük írható körök ,,ugyanakkorák''. Legyen $a$ és $b$ két hiperciklus, amelyek közös végpontjai $A$ és $B$. Az $AB$ szakasz felezőmerőlegese legyen $f$, jelölje $f$ metszéspontját $a$-val, $b$-vel és az $AB$ egyenessel rendre $U$, $V$, illetve $F$. Az $a$-ra egy tetszőleges $X$ pontjában állítsunk egy merőleges $e$ ,,egyenest'', ennek végpontjai legyenek $C$ és $D$, metszéspontja $b$-vel $Y$, és az $e$ félkör középpontja legyen $O$. Azt fogjuk igazolni, hogy $e$ és $b$ is merőlegesen metszik egymást, létezik egy $k$ kör, amely az $X$ és $Y$ pontokban érinti az $a$, illetve a $b$ görbét, és $d\left(X\mathrm{,}Y\right)=d\left(U\mathrm{,}V\right)$ (7. ábra).     7. ábra   Az $O$ pontnak az $a$ körívre vonatkozó hatványából kapjuk, hogy $O{Y}^2=O{X}^2=OA\cdot OB$, így az $e$ félkör $OY$ sugara érinti $b$-t. Tehát az $e$ ,,egyenes'' a $b$ hiperciklust is merőlegesen metszi. Az a $k$ kör, amely az $X$ és $Y$ pontokban érinti az $OX$ és $OY$ szakaszokat, érinti az $a$ és $b$ görbéket is. Szükségünk lesz arra, hogy a $C\mathrm{,}X\mathrm{,}U$ pontok, illetve a $C\mathrm{,}Y\mathrm{,}V$ pontok is egy egyenesre esnek. Legyen $P$ az $OY$ egyenes és a $b$ körív $V$-beli érintőjének metszéspontja; mivel $V$ a $b$ felezőpontja, a $PV$ egyenes párhuzamos az $AB$ egyenessel. Az $OYC$ és a $PYV$ háromszög is egyenlő szárú, így $OYC\sphericalangle =YCO\sphericalangle =YVP\sphericalangle =PYV\sphericalangle$; ez mutatja, hogy a $CY$ és az $YV$ szakasz egymás meghosszabbítása. Ugyanígy igazolhatjuk, hogy $C$, $X$ és $U$ egy egyenesen van. A $CDX$ és a $CUF$ derékszögű háromszögek, továbbá a $CDY$ és a $CVF$ derékszögű háromszögek is hasonlók, ezért ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{CX\cdot YD}{CY\cdot XD}=\frac{CX}{XD}\cdot \frac{YD}{CY}=\frac{CF}{FU}\cdot \frac{FV}{CF}=\frac{FV}{FU};}\hfill \\ \hfill {\displaystyle d\left(X\mathrm{,}Y\right)=k\cdot \text{ln}\frac{CX\cdot YD}{CY\cdot XD}=k\cdot \text{ln}\frac{FV}{FV}=d\left(U\mathrm{,}V\right)\mathrm{.}}\hfill \end{array}}$ Ez mutatja, hogy bármelyik $X$ pontban ,,ugyanakkora'' kört lehet a két hiperciklus közé írni.   Horociklusok A horociklusok (más néven paraciklusok) olyan, a félsíkmodellben körvonalnak vagy egyenesnek látszó görbék, amelyeknek egyetlen pontjuk van a modell határán; más szóval, a határegyenest érintő körvonalak (8.a ábra), és a határegyenessel párhuzamos egyenesek (8.b ábra). A 8.a ábrán megfigyelhetjük, hogy a közös végpontú horociklusoknak megfelelő körvonalak hatványvonala a közös érintő, vagyis ismét csak a félsíkmodell határegyenese. 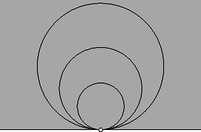    8. a ábra       8. b ábra   A közös végpontú horocikluspárokra is igaz, hogy a ,,távolságuk'' állandó, avagy a közéjük írt körök ,,ugyanakkorák''. Ennek igazolása a hiperciklusokra elmondott gondolatmenet leegyszerűsítésével történhet: a különbség annyi, hogy az $A$, $B$, $D$ pontok egybeesnek (9. ábra). Ennek részletes végiggondolását az Olvasóra hagyjuk. 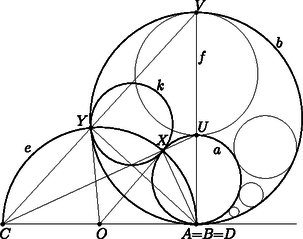    9. ábra   A sokféle, körvonalnak látszó görbét egy közös rajzon mutatja a 10. ábra: 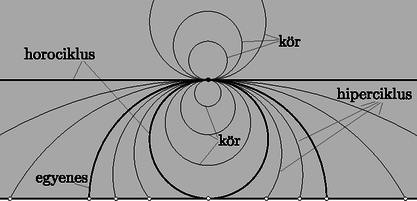    10. ábra     Érintő körös feladatok A kimerítő előkészületek után nézzünk példákat arra, hogy sínpárok kereszteződéseiből hogyan lehet feladatokat készíteni.   Ali Khezeli megoldása az olimpiai feladatjavaslatra Az előző részben látott olimpiai feladat javaslatra (11.a ábra) az iráni csapat egyik megfigyelője, Ali Khezeli mutatta nekem a következő megoldást.     11. a ábra   Tekintsük a 11.a ábrát egy félsíkmodellbeli rajznak. Az $a_2$ és $a_3$ hiperciklusok ,,távolsága'' ugyanakkora, mint a $b_1$ és a $b_2$ hiperciklusok ,,távolsága'': a közös ,,távolság'' a $b_1{a}_2{b}_2{a}_3$ tartományba írt kör ,,átmérője''. Ugyanígy, az $a_1$ és $a_2$ hiperciklusok ,,távolsága'' ugyanakkora, mint a $b_1$ és a $b_2$ hiperciklusok ,,távolsága'', továbbá az $a_1$ és $a_2$ hiperciklusok ,,távolsága'' is ugyanakkora, mint a $b_2$ és a $b_3$ hiperciklusok ,,távolsága''. Tehát az $a_2$ és $a_3$ hiperciklusok ,,távolsága'' ugyanakkora, mint a $b_2$ és a $b_3$ hiperciklusok ,,távolsága'', ezért az $a_2{b}_2{a}_3{b}_3$ tartományba is kör írható. A megoldás általánosabban is működik, például a 11.b ábrán látható esetben. 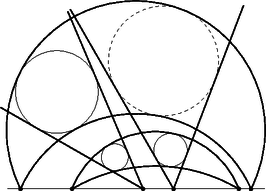    11. b ábra     Hiperciklusok egy kör középpontján keresztül Eddig a különböző görbepárok távolságát a közéjük írt körök átmérőivel mértük meg. Megtehetjük azonban azt is, hogy egy körhöz csak egy érintő hiperciklust rajzolunk, a másik hiperciklus a kör középpontján megy át. Legyen $ABC$ hegyesszögű háromszög, a magasságai $A{A}_1$, $B{B}_1$ és $C{C}_1$, az $A{A}_1$ magasság és a $B{C}_1{B}_{1}C$ félkör metszéspontja $K$. Húzzunk a $B$ és a $C$ pontból érintőket az $A{B}_1{C}_1$ körhöz a háromszög belsejében, az érintő félegyenesek legyenek $b$ és $c$ (12. áb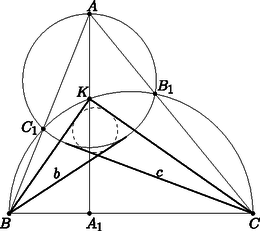ra).     12. ábra   Ezeket a köröket és a $K$ pontot már ismerjük a 3. ábráról: az $A_{1}A$ és a $BC$ hiperbolikus ,,egyenes'' is merőlegesen metszi az $A{B}_1{C}_1$ kört, ezért $K$ a kör ,,középpontja''. A $BK$ és a $b$ hiperciklus ,,távolsága'', valamint a $CK$ és a $c$ hiperciklus ,,távolsága'' is az $A{B}_1{C}_1$ kör ,,sugara''. Ezért a két hipercikluspár közé közös érintő kört lehet írni.   Távolságok összeadása Ha ugyanazokkal a végpontokkal nem két, hanem három hiperciklust rajzolunk, a közöttük mért ,,távolságokat'' összeadhatjuk. A 13.a ábrán az $a_1$ és $a_2$ hiperciklusok ,,távolsága'' a közéjük írt $k_2$ kör ,,átmérője'', míg az $a_2$ és $a_3$ ,,távolsága'' a $k_1$ ,,átmérője''; az $a_1$ és $a_3$ közötti ,,távolság'' a kettő összege.     13. a ábra   Ugyanezt az összeget kapjuk a $b_1$ és $b_3$ közötti ,,távolságra'' (csak fordított sorrendben), tehát az $a_1{b}_3{a}_3{b}_1$ négyszögbe is kört lehet írni. Ugyanez elmondható a 13.b ábrán is. 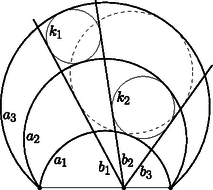    13. b ábra     Érintőnégyszögek egy jellemzése A félegyenesnek látszó hiperciklusok ,,távolsága'' könnyen felírható szögekkel. Legyen $a$ és $b$ két hiperciklus, amelyek egyik végpontja $O$, a másik végpont az ideális pont, és metsszük el ezeket egy $O$ középpontú félkörrel a 14.a ábra szerint. 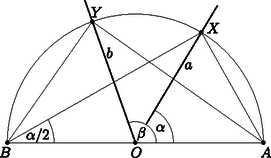    14. a ábra   Az ábrán feltüntetett szögekkel, feltéve, hogy $\alpha <\beta$, az $OXB$ egyenlő szárú háromszögből azt kapjuk, hogy $ABX\sphericalangle =\frac{1}{2}AOX\sphericalangle =\frac{\alpha }{2}$, ezért $\frac{AX}{XB}=\text{tg}\frac{\alpha }{2}$, és hasonlóan $\frac{AY}{YB}=\text{tg}\frac{\beta }{2}$. Tehát az $a$ és a $b$ hiperciklus közötti ,,távolság'' 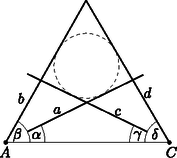$\begin{array}{c}{\displaystyle d\left(X\mathrm{,}Y\right)=k\cdot \text{ln}\frac{AY\cdot XB}{AX\cdot YB}=k\cdot \text{ln}\frac{\text{tg}\frac{\beta }{2}}{\text{tg}\frac{\alpha }{2}}\mathrm{.}}\end{array}$     14. b ábra   Most tekintsünk két félegyenes-párt, az $a\mathrm{,}b$ és $c\mathrm{,}d$ hiperciklusokat a 14.b ábra szerint. A közös érintő kör akkor és csak akkor létezik, ha az $a$ és $b$ ,,távolsága'' megegyezik $c$ és $d$ ,,távolságával'', vagyis $\begin{array}{c}{\displaystyle \frac{\text{tg}\frac{\beta }{2}}{\text{tg}\frac{\alpha }{2}}=\frac{\text{tg}\frac{\delta }{2}}{\text{tg}\frac{\gamma }{2}}\mathrm{.}}\end{array}$ A feltétel akkor is érvényes marad, ha az $a$ és a $c$ félegyenest az $AC$ egyenes másik oldalára rajzoljuk (15a. ábra). 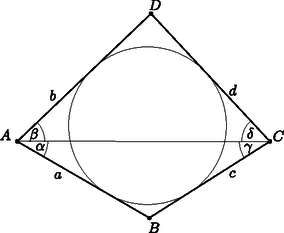    15. a ábra   Az érintőnégyszögeknek ezt a tulajdonságát érdemes külön is kimondani és megtanulni:   Lemma. Legyen az $ABCD$ konvex négyszögben $\alpha =CAB\sphericalangle$, $\beta =DAC\sphericalangle$, $\gamma =BCA\sphericalangle$ és $\delta =ACD\sphericalangle$. Az $ABCD$ négyszög akkor és csak akkor érintőnégyszög, ha $\begin{array}{c}{\displaystyle \frac{\text{tg}\frac{\beta }{2}}{\text{tg}\frac{\alpha }{2}}=\frac{\text{tg}\frac{\delta }{2}}{\text{tg}\frac{\gamma }{2}}\mathrm{.}}\end{array}$   A Lemma bizonyítását kezdjük a ,,csak akkor'' iránnyal; tegyük fel, hogy $ABCD$ érintőnégyszög, a beírt köre $k$, az érintési pontok $X$, $Y$, $Z$ és $W$ a 15.b ábra szerint. Az általánosság csorbulása nélkül feltehetjük, hogy 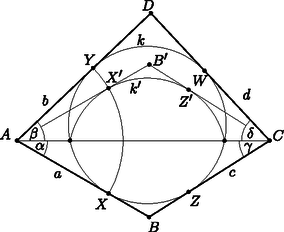$\beta \ge \alpha$.     15. b ábra   Tükrözzük az $AC$ átlóra a $B$, $X$, $Z$ pontokat és a $k$ körnek az $ABC$ háromszögbe eső ívét; a tükörképeket jelölje rendre $B\text{'}$, $X\text{'}$, $Z\text{'}$, illetve $k\text{'}$. Az $A$ pontból a $k$-hoz és $k\text{'}$-höz húzott érintők egyenlők, ezért az $XX\text{'}Y$ kör középpontja $A$. Ha az $AC$ egyenesnek a $D$-vel azonos oldalát a félsíkmodellnek tekintjük, akkor a $k$ és $k\text{'}$ hiperciklusok ,,távolsága'' $\begin{array}{c}{\displaystyle d\left(X\text{'}\mathrm{,}Y\right)=k\cdot \text{ln}\frac{\text{tg}\frac{\beta }{2}}{\text{tg}\frac{\alpha }{2}}\mathrm{.}}\end{array}$ Ugyanezt az $A$ helyett a $C$ ponttal is elmondhatjuk, és a $k$ és $k\text{'}$ hiperciklusok ,,távolságára'' így azt kapjuk, hogy $\begin{array}{c}{\displaystyle d\left(Z\text{'}\mathrm{,}W\right)=k\cdot \text{ln}\frac{\text{tg}\frac{\delta }{2}}{\text{tg}\frac{\gamma }{2}}\mathrm{.}}\end{array}$ A kétféle képlet összehasonlításából $\begin{array}{c}{\displaystyle \frac{\text{tg}\frac{\beta }{2}}{\text{tg}\frac{\alpha }{2}}=\frac{\text{tg}\frac{\delta }{2}}{\text{tg}\frac{\gamma }{2}}\mathrm{.}}\end{array}$ A megfordításhoz most tegyük fel, hogy $ABCD$ nem érintőnégyszög. Vegyük fel az $AD$ félegyenesen azt a $D_0$ pontot, amelyre $ABC{D}_0$ érintőnégyszög, és legyen ${\delta }_0=AC{D}_0\sphericalangle \ne \delta$. Az előbbiek szerint 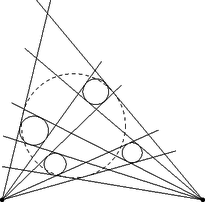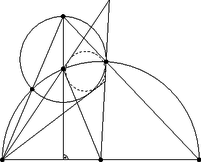$\begin{array}{c}{\displaystyle \frac{\text{tg}\frac{\beta }{2}}{\text{tg}\frac{\alpha }{2}}=\frac{\text{tg}\frac{{\delta }_0}{2}}{\text{tg}\frac{\gamma }{2}}\ne \frac{\text{tg}\frac{\delta }{2}}{\text{tg}\frac{\gamma }{2}}\mathrm{.}}\end{array}$   Feladatok   1. Feladatok szöveg nélkül:           KöMaL A. 621., 2014/9 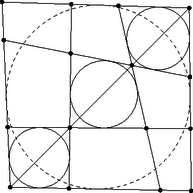 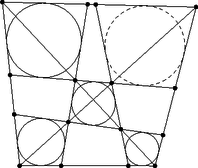       IZhO 2014/4; Nairi Sedrakyan feladata     2. Az $ABCD$ konvex érintőnégyszögbe írt kör középpontja $I$. Az $AB$ és a $DC$ félegyenes az $F$ pontban, az $AD$ és a $BC$ félegyenes a $G$ pontban metszi egymást. Legyen $\text{E}$ az a $F$, $G$ fókuszú ellipszis, amely átmegy a $B$ és $D$ pontokon, és legyen $\text{H}$ az a $F$, $G$ fókuszú hiperbolaág, amely átmegy az $A$ és $C$ pontokon. Az $\text{E}$ és $\text{H}$ metszéspontjait jelölje $P$ és $Q$. Mutassuk meg, hogy a $P$, $Q$ és $I$ pontok egy egyenesen vannak. (KöMaL A. 630., 2014. december)   3. Adott az $O{A}_1{A}_2{A}_3$ tetraéder mindegyik $O{A}_i$ élén egy $B_i$ belső pont, az $O{A}_i$ él $A_i$-n túli meghosszabbításán pedig egy $C_i$ pont ($i=\mathrm{1,2,3}$). Tegyük fel, hogy az $O{A}_{i+1}{A}_{i+2}$ és $B_i{A}_{i+1}{A}_{i+2}$ síkok által határolt hat lapú testbe, továbbá az $B_i{A}_{i+1}{A}_{i+2}$ és $C_i{A}_{i+1}{A}_{i+2}$ síkok által határolt testbe is egy-egy gömböt lehet írni. Bizonyítsuk be, hogy ekkor az $O{A}_{i+1}{A}_{i+2}$ és $C_i{A}_{i+1}{A}_{i+2}$ síkok által határolt testbe is gömböt lehet írni. (KöMaL A. 547., 2011. november) 1A cikksorozat a Rényi Intézet és a Sztaki támogatásával készült.