Cím:	Megoldásvázlatok a 2020/1. szám emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Balga Attila (Budapest)
Füzet:	2020/február, 82 - 90. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Oldjuk meg a következő egyenleteket a valós számok halmazán: $a)$ $\text{cos}2x+3\cdot \text{cos}x-1=0$,  (7 pont) $b)$ $\sqrt[]{6-x}-\sqrt[]{5-2x}=1$.  (6 pont)   Megoldás. $a)$ ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2\cdot \text{cos}{}^{2}x-1+3\cdot \text{cos}x-1}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle 2\cdot \text{cos}{}^{2}x+3\text{cos}x-2}& {\displaystyle =0.}\hfill \end{array}}$ Ebből:   $\text{cos}x=-2$ vagy $\text{cos}x=\frac{1}{2}$. A $\text{cos}x=-2$ egyenletnek nincs megoldása, mert $-1\le \text{cos}x\le 1$. Ha $\text{cos}x=\frac{1}{2}$, akkor $x=\frac{\pi }{3}+2k\pi$, $k\in \text{Z}$, vagy $x=-\frac{\pi }{3}+2l\pi$, $l\in \text{Z}$. Ekvivalens átalakításokat végeztünk, tehát a kapott gyökök kielégítik az eredeti egyenletet. $b)$ $x\le 6$ és $x\le 2\mathrm{,}5\Rightarrow x\le 2\mathrm{,}5$. $\begin{array}{c}{\displaystyle \sqrt[]{6-x}=1+\sqrt[]{5-2x}\mathrm{.}}\end{array}$ Mivel a négyzetgyök definíciója alapján egyik oldal sem negatív, a négyzetre emelés ekvivalens átalakítás: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 6-x}& {\displaystyle =1+5-2x+2\cdot \sqrt[]{5-2x}\mathrm{,}}\hfill \\ \hfill {\displaystyle x}& {\displaystyle =2\cdot \sqrt[]{5-2x}\mathrm{.}}\hfill \end{array}}$ A négyzetgyök definíciója alapján $x\ge 0$. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x^2}& {\displaystyle =20-8x\mathrm{,}}\hfill \\ \hfill {\displaystyle x^2+8x-20}& {\displaystyle =\mathrm{0,}}\hfill \end{array}}$ $x_1=-10$, $x_2=2$. A feltétel miatt csak az $x=2$ megoldás. Az alaphalmazon ekvivalens átalakításokat végeztünk, tehát a kapott gyök kielégíti az eredeti egyenletet.   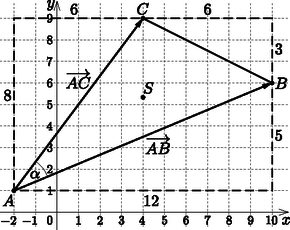2. A nem is olyan távoli jövőben a fizika fakultációsok online szimulációban vizsgálhatják töltött részecskék viselkedését mágneses mezőben, ahol a részecskék helyzetét derékszögű koordináta-rendszer segítségével írják le. Két fizika fakultációs diák, Hácé és Kácé fontos kísérletet tervez: egy háromszög csúcsaiba $(A\left(-2;1\right)$; $B\left(10;6\right)$; $C\left(4;9\right))$ Kácé három detektort helyez. Hácé ekkor egy töltött részecskét juttat a háromszög súlypontjába. A töltött részecske tömege peti-ben (peti: tömegegység a szimulációban) a háromszög területének és a $BAC\sphericalangle$ cosinusának szorzata. Határozzuk meg a háromszög súlypontjának koordinátáit és a részecske tömegének pontos értékét.  (12 pont) Megoldás. A súlypontra vonatkozó képlet alapján: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle s_1=\frac{-2+10+4}{3}}& {\displaystyle =\mathrm{4,}}\hfill \\ \hfill {\displaystyle s_2=\frac{1+6+9}{3}}& {\displaystyle =\frac{16}{3}\mathrm{.}}\hfill \end{array}}$     Tehát a súlypont: $S(4;\frac{16}{3})$. Az ábra jelöléseit követve: a háromszög területét megkapjuk, ha a köré írt téglalap területéből kivonjuk a derékszögű háromszögek területét. Így: $\begin{array}{c}{\displaystyle T_{ABC}=8\cdot 12-\frac{1}{2}\cdot 6\cdot 8-\frac{1}{2}\cdot 6\cdot 3-\frac{1}{2}\cdot 12\cdot 5=33.}\end{array}$ $\overrightarrow{AC}\left(6;8\right)$, így $|\overrightarrow{AC}|=10$; $\overrightarrow{AB}\left(12;5\right)$, így $|\overrightarrow{AB}|=13$. Az $\overrightarrow{AC}$ és $\overrightarrow{AB}$ vektorok skaláris szorzatát kétféle módon felírva: $\begin{array}{c}{\displaystyle \overrightarrow{AC}\cdot \overrightarrow{AB}=|\overrightarrow{AC}|\cdot |\overrightarrow{AB}|\cdot \text{cos}\alpha =6\cdot 12+8\cdot 5=\mathrm{112,}}\end{array}$ ekkor $\text{cos}\alpha =\frac{56}{65}$. Tehát a részecske tömegének pontos értéke: $\frac{1848}{65}$ peti.   3. Pébé tanár úr, a $C$ osztály osztályfőnöke lelkesen érkezett a reggeli órára. ‐ Képzeljétek, megálmodtam a matematika emelt szintű érettségi átlagunkat! ‐ És mennyi volt, tanár úr? ‐ Azt sajnos elfelejtettem, de emlékszem, hogy a $D$-sek átlaga szabályos közelítéssel 84,3, az $E$-seké 85,1, a három osztály átlaga pedig 87,9 volt. Tudjuk, hogy a $D$-ből $11$-en, az $E$-ből $14$-en, tőlünk pedig $24$-en írnak emelt szintű érettségit. Ebből már ki lehet számolni az osztályátlagot. $a)$ Mennyi a $C$-sek osztályátlaga egy tizedesjegyre kerekítve, ha minden diák érettségi eredménye csak egész százalék lehet?  (8 pont) A Szalagavató nyitótáncában a $C$-sek $20\%$-a, a $D$-sek $25\%$-a vesz részt. Az egyik szünetben $4$ fő $C$ osztályos és $2$ fő $D$ osztályos tanuló vásárolt pizzát a büfében. $b)$ Mennyi annak a valószínűsége, hogy közülük pontosan ketten táncolnak a nyitótáncban?  (6 pont)   Megoldás. $a)$ Legyen a $D$-sek százalékainak összege $d$, az $E$-seké $e$, a $C$-seké $c$, a három osztályé pedig $h$. A kerekítés szabályainak megfelelően: $\begin{array}{c}{\displaystyle 84\mathrm{,}25\le \frac{d}{11}<84\mathrm{,}35\Rightarrow 926\mathrm{,}75\le d<927\mathrm{,}\mathrm{85,}}\end{array}$ így $d=927$, $\begin{array}{c}{\displaystyle 85\mathrm{,}05\le \frac{e}{14}<85\mathrm{,}15\Rightarrow 1190\mathrm{,}7\le e<1192\mathrm{,}\mathrm{1,}}\end{array}$ így $d=1191$, vagy $d=1192$, $\begin{array}{c}{\displaystyle 87\mathrm{,}85\le \frac{h}{49}<87\mathrm{,}95\Rightarrow 4304\mathrm{,}65\le h<4309\mathrm{,}\mathrm{55,}}\end{array}$ így $h$ lehet 4305, 4306, 4307, 4308, 4309. Foglaljuk a kapott eredményeket egy táblázatba:     (A táblázatban a $c=h-d-e$ és a $C_{\text{átlag}}=\frac{c}{24}$ képleteket alkalmaztuk.) Tehát a $C$-sek átlaga 91,1; 91,2 vagy 91,3 lehet. $b)$ A binomiális eloszlás képletét felhasználva: 1) Mindketten $D$-sek:   $\begin{array}{c}{\displaystyle p_D=\left(\genfrac{}{}{0ex}{}{2}{2}\right)\cdot 0\mathrm{,}{25}^2\cdot 0\mathrm{,}{75}^0\cdot \left(\genfrac{}{}{0ex}{}{4}{0}\right)\cdot 0\mathrm{,}{2}^0\cdot 0\mathrm{,}{8}^4=\frac{16}{625}=0\mathrm{,}0256.}\end{array}$   2)Mindketten$C$-sek:   $\begin{array}{c}{\displaystyle p_C=\left(\genfrac{}{}{0ex}{}{4}{2}\right)\cdot 0\mathrm{,}{2}^2\cdot 0\mathrm{,}{8}^2\cdot \left(\genfrac{}{}{0ex}{}{2}{0}\right)\cdot 0\mathrm{,}{25}^0\cdot 0\mathrm{,}{75}^2=\frac{54}{625}=0\mathrm{,}0864.}\end{array}$   3)Egyikük$C$-s,másikuk$D$-s:   $\begin{array}{c}{\displaystyle p_{CD}=\left(\genfrac{}{}{0ex}{}{4}{1}\right)\cdot 0\mathrm{,}2\cdot 0\mathrm{,}{8}^3\cdot \left(\genfrac{}{}{0ex}{}{2}{1}\right)\cdot 0\mathrm{,}25\cdot 0\mathrm{,}75=\frac{96}{625}=0\mathrm{,}1536.}\end{array}$   Ígyannakvalószínűsége,hogypontosankettentáncolnaka nyitótáncban:   $\begin{array}{c}{\displaystyle p=\frac{16}{625}+\frac{54}{625}+\frac{96}{625}=\frac{166}{625}=0\mathrm{,}2656.}\end{array}$     4. Adottak az $f:\text{R}\to \text{R}$, $f\left(x\right)=x^3-8$ és a $g:\text{R}\to \text{R}$, $g\left(x\right)=4-2x$ függvények. $a)$ Adjuk meg a $g\circ f$ függvény $x=2$ abszcisszájú pontjába húzott érintő egyenletét.  (7 pont) $b)$ Adjuk meg a $\underset{x\to 2}{\overset{}{\underset{}{\overset{}{\text{lim}}}}}\frac{f}{g}$ határértéket.  (5 pont)   Megoldás. $a)$ Legyen $h=g\circ f$, ekkor $h\left(x\right)=4-2\cdot \left(x^3-8\right)=20-2x^3$. Az adott pontba húzott érintő iránytangense a függvény deriváltjának helyettesítési értéke az adott helyen:   $\begin{array}{c}{\displaystyle h\text{'}\left(x\right)=-6x^2;h\text{'}\left(2\right)=-24;E\left(2;4\right)\mathrm{,}}\end{array}$   Azérintőegyenlete:$y-4=-24$ \cdot $(x-2)\; \iff 24x+y-52=0$. $\begin{array}{c}{\displaystyle \underset{}{\overset{}{}}}\end{array}$limx$\to$2 $\frac{x^3-8}{4-2x}$=limx$\to$2 $\frac{\left(x-2\right)\cdot \left(x^2+2x+4\right)}{-2\cdot \left(x-2\right)}$=limx$\to$2 $\frac{x^2+2x+4}{-2}$=-6.   (*)   II. rész     5. Két birkózó egyesület közös bajnokságra készül. A felkészülés során előírás a napi $8$ óra alvás. A korábbi felkészülések során kiderült, hogy a felkészülés hatékonyságát jelentősen befolyásolja a regenerálódásra fordított idő. A szakemberek megállapították, hogy a hatékonyságot az $E\left(t\right)=t^3\cdot \left(3\mathrm{,}2-t\right)$ függvénnyel lehet leírni, ahol $t$ a regenerálódásra fordított idő. $a)$ Mennyi időt fordítsanak a regenerálódásra, hogy a felkészülés a lehető leghatékonyabb legyen?  (8 pont) A bajnokságot kieséses rendszerben folytatják le, a párokat minden egyes mérkőzés előtt véletlenszerűen sorsolják. Az első pár sorsolásakor $\frac{7}{40}$ a valószínűsége annak, hogy mindkét versenyző az $A$ egyesület tagja. Két mérkőzés után, ahol egy résztvevőt az $A$, három résztvevőt pedig a $B$ egyesületből sorsoltak ki, ugyanakkora valószínűséggel sorsolják mindkét versenyzőt az $A$ egyesületből, mint a $B$ egyesületből. $b)$ Hányan indultak a bajnokságon az egyes egyesületekből?  (8 pont)   Megoldás. $a)$ $E\left(t\right)=3\mathrm{,}2t^3-t^4$. A függvény szélsőértékét a derivált segítségével határozzuk meg: $\begin{array}{c}{\displaystyle E\text{'}\left(t\right)=9\mathrm{,}6t^2-4t^3\mathrm{.}}\end{array}$ A függvénynek ott lehet szélsőértéke, ahol a deriváltja nulla és a második derivált nem nulla: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 9\mathrm{,}6t^2-4t^3}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle 4t^2\cdot \left(2\mathrm{,}4-t\right)}& {\displaystyle =\mathrm{0,}}\hfill \end{array}}$ $t=0$ vagy $t=2\mathrm{,}4$. A második derivált: $E\text{'}\text{'}\left(t\right)=19\mathrm{,}2t-12t^2$, $E\text{'}\text{'}\left(0\right)=0$ és $E\text{'}\text{'}\left(2\mathrm{,}4\right)=$ =-23,04<0. Mivel $t\in \left[0;16\right]$, meg kell vizsgálnunk a függvény helyettesítési értékeit az intervallum határaiban: $E\left(0\right)=0$ és $E\left(16\right)=-52428\mathrm{,}8$. Tehát a felkészülés akkor a leghatékonyabb, ha a regenerálódásra fordított idő 2,4 óra. $b)$ Mivel két mérkőzés után megegyezik annak a valószínűsége, hogy mindkét versenyzőt az $A$, illetve a $B$ egyesületből sorsolják, ezért két mérkőzés után ugyanannyi versenyző maradt az $A$ egyesületből, mint a $B$ egyesületből. Legyen ez a szám $x$. Ekkor eredetileg $x+1$ versenyző indult az $A$ egyesületből és $x+3$ versenyző a $B$ egyesületből, tehát összesen $2x+4$ versenyző indult a bajnokságon. Ekkor az $A$ egyesületből $\left(\genfrac{}{}{0ex}{}{x+1}{2}\right)$-féleképpen választhattuk a két versenyzőt, az összes versenyző közül pedig $\left(\genfrac{}{}{0ex}{}{2x+4}{2}\right)$-féleképpen. Így annak valószínűsége, hogy az első pár sorsolásakor mindkettőt az $A$ egyesületből választották: $\begin{array}{c}{\displaystyle \frac{\left(\genfrac{}{}{0ex}{}{x+1}{2}\right)}{\left(\genfrac{}{}{0ex}{}{2x+4}{2}\right)}=\frac{7}{40}\iff \frac{\frac{\left(x+1\right)\cdot x}{2}}{\frac{\left(2x+4\right)\cdot \left(2x+3\right)}{2}}=\frac{7}{40}\mathrm{.}}\end{array}$ Ebből $6x^2-29x-42=0$, $x_1=-\frac{7}{6}$; $x_2=6$. Nyilván csak az $x=6$ lehet megoldás. Ellenőrzés: Ha az $A$ egyesületből 7, a $B$ egyesületből 9 versenyző indult, akkor két $A$-beli versenyzőt választhatjuk $\left(\genfrac{}{}{0ex}{}{7}{2}\right)=21$-féleképpen.   Két versenyzőt összesen $\left(\genfrac{}{}{0ex}{}{16}{2}\right)=120$-féleképpen választhatunk. Annak valószínűsége, hogy mindkét versenyzőt az $A$ klubból választottuk: $\frac{21}{120}=\frac{7}{40}$. Tehát az $A$ klubból 7-en, a $B$ klubból 9-en indultak a versenyen.   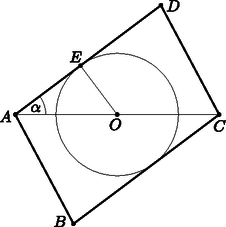6. Egy paralelogramma alakú füves terület oldalai 50 m és 34 m, az oldalak végpontjait összekötő átló 56 m hosszú. Az átló egy pontjába egy önműködő locsoló berendezést helyezünk, amely a terület bármely pontjából eléri bármely másik pontját, és ha a távolságot beállítottuk, akkor egy körön belül mindent lelocsol. $a)$ Legalább mekkora területet kell kézzel locsolni, ha a locsoló berendezés a terület határán túl nem locsolhat?  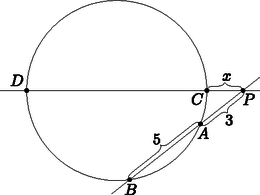(10 pont) A füves területen egy kör alakú virágágyást alakítanak ki. A virágágyást két egyenes gyalogút szeli át, amelyek egy a körön kívüli $P$ pontban metszik egymást. A virágágyást az egyik gyalogút az $A$ és $B$, a másik gyalogút a $C$ és $D$ pontokban metszi. Tudjuk, hogy $PA=3\text{m}$, $AB=5\text{m}$, valamint $PD=PC+10\text{m}$. $b)$ Mekkora a $PD$ távolság?  (6 pont)   Megoldás. $a)$ Keressük azt a kört, amely a paralelogrammába beírható, középpontja az átlón van és sugara a legnagyobb. Ez a kör a paralelogramma két szemközti, hosszabb oldalát érintő kör, ebből következően ‐ szimmetria okokból ‐ középpontja a paralelogramma átlójának felezőpontja lesz, hiszen bármely más középpont esetén a kör sugara kisebb lesz, vagy metszi valamelyik oldalt a két szemközti oldal közül.     Felírva a cosinustételt az $ACD$ háromszög $CD$ oldalára: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle D{C}^2}& {\displaystyle =A{C}^2+A{D}^2-2\cdot AC\cdot AD\cdot \text{cos}\alpha \mathrm{,}}\hfill \\ \hfill {\displaystyle }\end{array}}$ 342=502+562-2⋅50⋅56⋅cosα, cosα=45. Mivel $\alpha <{90}^{\circ }$, ezért $\begin{array}{c}{\displaystyle \text{sin}\alpha =\sqrt[]{1-{\left(\frac{4}{5}\right)}^2}=\frac{3}{5}\mathrm{.}}\end{array}$ Mivel az érintő merőleges a sugárra, ezért az $AOE$ derékszögű háromszögben: $\begin{array}{c}{\displaystyle r=AO\cdot \text{sin}\alpha =\frac{84}{5}\approx 16\mathrm{,}8\text{m}\mathrm{.}}\end{array}$ Ekkor a kör területe: 886,7 m${}^2$. A paralelogramma területe: $\begin{array}{c}{\displaystyle T_{ABCD}=2\cdot \frac{1}{2}\cdot AC\cdot AD\cdot \text{sin}\alpha =2\cdot \frac{1}{2}\cdot 56\cdot 50\cdot \frac{3}{5}=1680{\text{m}}^2\mathrm{.}}\end{array}$ Tehát kb. 793,3 m${}^2$ területet kell kézzel locsolni.     $b)$ A külső pontból a körhöz húzott szelő és érintő szakaszok tétele alapján: ${\displaystyle \begin{array}{c}\hfill {\displaystyle PA\cdot PB=PC\cdot PD\mathrm{,}}\hfill \\ \hfill {\displaystyle 24=x\cdot \left(x+10\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle x^2+10x-24=\mathrm{0,}}\hfill \\ \hfill {\displaystyle x_1=2;x_2=-12.}\hfill \end{array}}$ Tehát a $PD$ távolság 12 m.   7. $a)$ Bizonyítsuk be, hogy a szomszédos páratlan számok reciprokainak különbsége egyenlő a számok szorzata reciprokának kétszeresével.  (4 pont) Adott az $\frac{1}{1\cdot 4}+\frac{1}{4\cdot 7}+\frac{1}{7\cdot 10}+\text{...}$ végtelen sor. $b)$ Bizonyítsuk be, hogy az $n$-edik részletösszeg: $\begin{array}{c}{\displaystyle S_n=\frac{n}{3n+1}\mathrm{.}}\end{array}$ (8 pont) $c)$ Adjuk meg a $\underset{n\to \infty }{\overset{}{\underset{}{\overset{}{\text{lim}}}}}\left(S_n\right)$ határértéket.  (4 pont)   Megoldás. $a)$ Legyenek a szomszédos páratlan számok: $2k-1$ és $2k+1$. $\begin{array}{c}{\displaystyle \frac{1}{2k-1}-\frac{1}{2k+1}=\frac{2k+1-\left(2k-1\right)}{\left(2k-1\right)\cdot \left(2k+1\right)}=\frac{2}{\left(2k-1\right)\cdot \left(2k+1\right)}\mathrm{.}}\end{array}$ $b)$ A nevezőkben található szorzatok első tényezői egy olyan számtani sorozatot alkotnak, amelynek első eleme 1, különbsége 3. Így a részletösszeg $i$-edik tagjának nevezőjében található szorzat első tényezője: $1+\left(i-1\right)\cdot 3=3i-2$. Tehát a részletösszeg $i$-edik tagja: $\begin{array}{c}{\displaystyle \frac{1}{\left(3i-2\right)\cdot \left(3i+1\right)}}\end{array}$ Mivel $\begin{array}{c}{\displaystyle \frac{1}{3i-2}-\frac{1}{3i+1}=\frac{3i+1-\left(3i-2\right)}{\left(3i-2\right)\cdot \left(3i+1\right)}=\frac{3}{\left(3i-2\right)\cdot \left(3i+1\right)}\mathrm{,}}\end{array}$ a részletösszeg $i$-edik tagja: $\begin{array}{c}{\displaystyle \frac{1}{3}\cdot \left(\frac{1}{3i-2}-\frac{1}{3i+1}\right)\mathrm{.}}\end{array}$ Így az $n$-edik részletösszeg: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle }& {\displaystyle }\hfill & {\displaystyle \frac{1}{1\cdot 4}+\frac{1}{4\cdot 7}+\frac{1}{7\cdot 10}+\cdots +\frac{1}{\left(3n-2\right)\cdot \left(3n+1\right)}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =}\hfill & {\displaystyle \frac{1}{3}\cdot \left(\frac{1}{1}-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+\frac{1}{7}-\frac{1}{10}+\cdots +\frac{1}{3n-2}-\frac{1}{3n+1}\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =}\hfill & {\displaystyle \frac{1}{3}\cdot \left(1-\frac{1}{3n+1}\right)=\frac{1}{3}\cdot \frac{3n}{3n+1}=\frac{n}{3n+1}\mathrm{.}}\hfill \end{array}}$ Megjegyzés. A bizonyítás természetesen teljes indukcióval is elvégezhető. $\begin{array}{c}{\displaystyle \underset{n\to \infty }{\overset{}{\text{lim}}}\left(S_n\right)=\underset{n\to \infty }{\overset{}{\text{lim}}}\left(\frac{n}{3n+1}\right)=\underset{n\to \infty }{\overset{}{\text{lim}}}\left(\frac{\frac{n}{n}}{\frac{3n}{n}+\frac{1}{n}}\right)=\underset{n\to \infty }{\overset{}{\text{lim}}}\left(\frac{1}{3+\frac{1}{n}}\right)=\frac{1}{3}\mathrm{.}}\end{array}$ (*)     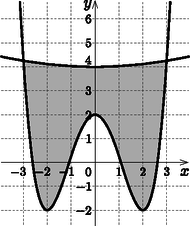8. Az ábrán egy nemzetközi fogász kongresszus emblémája látható. Az alakzatot az alábbi függvények grafikonjai határolják:     $\begin{array}{c}{\displaystyle f:\text{R}\to \text{R}\mathrm{,}x\mapsto \frac{1}{4}{x}^4-2x^2+2\text{és}g:\text{R}\to \text{R}\mathrm{,}x\mapsto \frac{1}{36}{x}^2+4.}\end{array}$ $a)$ Határozzuk meg a függvények grafikonjainak metszéspontjait.  (2 pont) $b)$ Mekkora az embléma területe, ha a koordináta-rendszer 1 egysége a valóságban 1 cm-nek felel meg? A konferencián egy asztalhoz került hat fogorvos, akik örömmel állapították meg, hogy valamennyien részt vesznek egy programban, amelyben hasznos kezelési eljárásokat osztanak meg egymással. Ennek keretében a hat fogorvos is kapcsolatban áll egymással, mindegyik mindegyikkel. A kapcsolattartás két hálózaton keresztül folyik, de két fogorvos egymás között mindig ugyanazon a hálózaton kommunikál.   (8 pont) $c)$ Bizonyítsuk be, hogy az asztalnál helyet foglaló hat fogorvos között van három olyan, aki egymás közt ugyanazon a hálózaton kommunikál.  (6 pont) Megoldás. $a)$ ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{1}{4}{x}^4-2x^2+2=\frac{1}{36}{x}^2+\mathrm{4,}}\hfill \\ \hfill {\displaystyle 9x^4-73x^2-72=\mathrm{0,}}\hfill \\ \hfill {\displaystyle x_1^2=-\frac{8}{9};x_2^2=9.}\hfill \end{array}}$ A két gyök közül csak $x^2=9$ ad megoldást, így a metszéspontok: $(-3;\frac{17}{4})$ és $(3;\frac{17}{4})$.     $b)$ ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T}& {\displaystyle =|{\int }_{-3}^3\left(\frac{1}{4}{x}^4-2x^2+2-\left(\frac{1}{36}{x}^2+4\right)\right)\text{d}x|=|{\int }_{-3}^3\left(\frac{1}{4}{x}^4-\frac{73}{36}{x}^2-2\right)\text{d}x|=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\left|{\left[\frac{1}{20}{x}^5-\frac{73}{108}{x}^3-2x\right]}_{-3}^3\right|=\left|\frac{243}{20}-\frac{73}{4}-6-\left(-\frac{243}{20}+\frac{73}{4}+6\right)\right|=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\left|-\frac{121}{5}\right|=24\mathrm{,}2}\hfill \end{array}}$ Tehát az embléma területe 24,2 cm${}^2$. $c)$ Jelölje a hálózatokat $H_1$, illetve $H_2$. Válasszunk ki egy fogorvost. Mivel két hálózat van és öt partner, ezért a skatulya-elv értelmében a fogorvos az egyik hálózaton legalább három kollégával kommunikál, legyen ez a hálózat $H_1$. Ha az így meghatározott legalább három fogorvos között van kettő, aki egymással a $H_1$ hálózaton kommunikál, akkor ők és az eredetileg kiválasztott fogorvos alkotja a keresett hármast, hiszen ők egymás között a $H_1$ hálózaton kommunikálnak. Ha a legalább három fogorvos között semelyik kettő nem kommunikál egymás közt a $H_1$ hálózaton, akkor ők egymás között csak a $H_2$ hálózaton kommunikálhatnak. Így viszont lesz közöttük három olyan, aki egymás közt a $H_2$ hálózaton kommunikál.   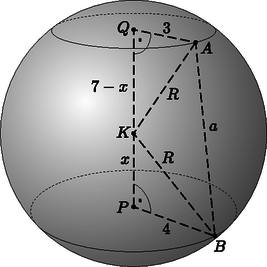9. Egy függönytartó rúd kúpban végződik. Rögzítő elemként egy $R$ sugarú gömböt kúposan átfúrunk úgy, hogy pontosan illeszkedjen a rúd végére, majd az így kapott testet ráhúzzuk úgy, hogy a kúp tengelye átmenjen a gömb középpontján. A rögzítőelem magassága 7 cm, a felső alapköre $r_1=3\text{cm}$, az alsó alapköre $r_2=4\text{cm}$ sugarú. $a)$ Határozzuk meg a rögzítőelem felszínét és térfogatát.  (10 pont) Az áruházban a függönytartó rudakat négyféle színben (arany, ezüst, fehér, fekete), a rögzítőelemet háromféle színben (arany, zöld és piros), a függönyöket ötféle színben (arany, ezüst, fehér, zöld, piros) árulják. $b)$ Hányféle kombinációt lehet összeállítani, ha az az előírás, hogy legalább az egyik elem aranyszínű legyen és a rúd két végén lévő rögzítőelem azonos színű?   Megoldás. $a)$ 1. eset: a gömb középpontja az alapkörök között van. A kapott test egy gömbréteg, amelyből kivágtak egy csonkakúpot. Az 1. ábrán látható $QAK$ és $PBK$ háromszögekre felírjuk Pitagorasz tételét: $\begin{array}{c}{\displaystyle {\left(7-x\right)}^2+3^2=R^2\text{és}{x}^2+4^2=R^2\mathrm{.}}\end{array}$ A két egyenletet kivonva egymásból: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 14x-42}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle x}& {\displaystyle =3.}\hfill \end{array}}$ Ekkor $R=5$ cm. A csonkakúp alkotójára felírva a Pitagorasz-tételt: $7^2+1^2=a^2$, így $a=5\sqrt[]{2}$. A rögzítőelem felszíne a gömböv és a csonkakúppalást felszínének összege: $\begin{array}{c}{\displaystyle A=2\pi Rm+\pi \left(r_1+r_2\right)a=70\pi +35\sqrt[]{2}\pi \approx 375\mathrm{,}4{\text{cm}}^2\mathrm{.}}\end{array}$ A rögzítőelem térfogatát megkapjuk, ha a gömbréteg térfogatából kivonjuk a csonkakúp térfogatát: $\begin{array}{c}{\displaystyle V=\frac{\pi }{6}m\left(m^2+3r_1^2+3r_2^2\right)-\frac{\pi }{3}m\left(r_1^2+r_2^2+r_1{r}_2\right)=\frac{434}{3}\pi -\frac{259}{3}\pi \approx \mathrm{183,3}{\text{cm}}^3\mathrm{.}}\end{array}$         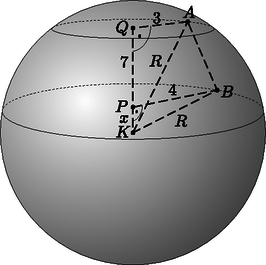2. eset: a gömb középpontja nincs az alapkörök között. A kapott test egy gömbréteg, amelyből kivágtak egy csonkakúpot. A 2. ábrán látható $QAK$ és $PBK$ háromszögekre felírjuk Pitagorasz tételét: $\begin{array}{c}{\displaystyle {\left(7+x\right)}^2+3^2=R^2\text{és}{x}^2+4^2=R^2\mathrm{.}}\end{array}$ A két egyenletet kivonva egymásból: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 14x+42}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle x}& {\displaystyle =-3.}\hfill \end{array}}$ Tehát ebben az esetben nincs megoldás. $b)$ A kombinációk számát úgy határozzuk meg, hogy az összes lehetséges eset számából kivonjuk a komplementer esemény (nincs aranyszínű elem) lehetőségeinek számát. Összes lehetőség: négyféle rúd, háromféle rögzítő elem és ötféle függöny, összesen: $4\cdot 3\cdot 5=60$. Komplementer: háromféle rúd, kétféle rögzítő elem, négyféle függöny, összesen: $3\cdot 2\cdot 4=24$. Tehát összesen $60-24=36$ olyan kombináció van, amelyben valamelyik elem aranyszínű.