Kezdőlap


Cím:	Térbe kilépő bizonyítások V.
Szerző(k):	Kós Géza
Füzet:	2020/február, 71 - 80. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egy olimpiai feladatjavaslat története

Ebben a cikksorozatban olyan bizonyításokat mutatunk be, amikor a geometriai alakzatokat ,,térbe kilépve'', három- vagy akár még magasabb dimenziós objektumok vetületeként vagy metszeteként állítjuk elő.
Ez a rész egy kicsit személyesebb lesz. Egy feladatjavaslat történetét mesélem el, amit a 2010-es Nemzetközi Matematikai Diákolimpiára (IMO) javasoltam.¹

A kiinduló feladat

Két pontból indítsunk három-három félegyenest úgy, hogy bármelyik két, különböző pontból induló egyenes elmetssze egymást; ezek a félegyenesek négy négyszöget határoznak meg. Igazoljuk, hogy ha a négyszögek közül valamelyik három érintőnégyszög, akkor a negyedik is érintőnégyszög (1. ábra).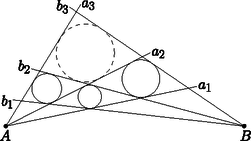

1. ábra

A feladatot sokféleképpen megoldhatjuk, például az előző részben bemutatott kúpokkal. Használjuk az 1. és a 2. ábra jelöléseit; feltesszük, hogy az

a_{1} b_{1} a_{2} b_{2}

, az

a_{1} b_{2} a_{2} b_{3}

, valamint az

a_{2} b_{1} a_{3} b_{2}

, négyszögek érintőnégyszögek, és ebből fogjuk megmutatni, hogy az

a_{2} b_{2} a_{3} b_{3}

négyszög is érintőnégyszög.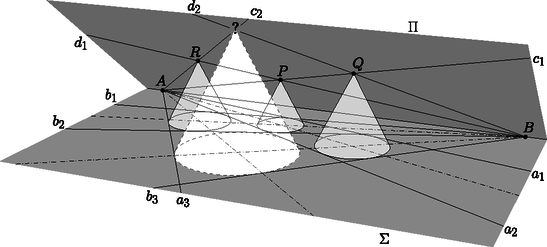

2. ábra

A tervünk az, hogy a

Σ

alapsíkunkból a térbe kilépbe, a négyszögekbe írt körökre egymáshoz hasonló kúpokat illesztünk, majd megszerkesztjük a negyedik kúpot. (A 2. ábrán olyan kúpokat rajzoltam, amelyek magassága kétszerese az alapkörük sugarának; a konkrét aránynak nincs jelentősége.)
Az olyan kúpoknak a csúcsai, amelyek alapköre érinti az

a_{1}

és

a_{2}

félegyeneseket, egy

A

-ból induló félegyenesen vannak; jelöljük ezt a félegyenest

c_{1}

-gyel. Hasonlóan, az

a_{2}

és

a_{3}

félegyeneseket, a

b_{1}

és

b_{2}

félegyeneseket, illetve a

b_{2}

és

b_{3}

félegyeneseket érintő körökre emelt kúpok csúcsai is egy-egy félegyenesen vannak; jelölje ezeket rendre

c_{2}

d_{1}

, illetve

d_{2}

(2. ábra).
A

c_{1}

és

d_{1}

félegyenesek a

P

pontban, az

a_{1} b_{1} a_{2} b_{2}

négyszögbe írt körhöz tartozó kúp csúcsában metszik egymást. Ugyanígy, a

c_{1}

és

d_{2}

, illetve a

c_{2}

és

d_{1}

is metszik egymást a másik két kúp csúcsában, a

Q

és a

P

pontban. A feladat állításához elég azt igazolnunk, hogy a

c_{2}

és a

d_{2}

félegyenes is elmetszi egymást, ugyanis a metszéspontjuk egyértelműen meghatározza a negyedik kúpot, amelynek alapköre érinti az

a_{2}

b_{2}

a_{3}

b_{3}

félegyenesek mindegyikét.
Legyen

Π

A B P

háromszög síkja. A

Q

pont a

c_{1} = A P

egyenesen, az

R

pont pedig a

d_{1} = B P

egyenesen van, tehát

Q, R \in Π

. Akkor viszont a

c_{2} = A R

és a

d_{2} = B Q

félegyenes is a

Π

síkban fekszik.
A

c_{2}

és a

d_{2}

félegyenesek

Σ

-ra való merőleges vetülete az

a_{2}

és az

a_{3}

, illetve a

b_{2}

és

b_{3}

szögfelezője, ezek az

a_{2} b_{2} a_{3} b_{3}

négyszög belsejében metszik egymást; a metszéspontjukat

Σ

-ra merőlegesen visszavetíthetjük

Π

-re, az így kapott pont

c_{2}

-nek és

d_{2}

-nek közös pontja, ami bizonyítja az állítást.

Valamikor 2009 őszén a 6-os villamoson kapaszkodva ezen a klasszikus feladaton gondolkodtam, akkor jöttem rá, hogy a bizonyítás hiperbolikus geometriában is elmondható, ha a kúpok hasonlósága helyett azt kötjük ki, hogy az alkotóik ugyanakkora szögben metszik az alapsíkot. Hazaérve megpróbáltam az észrevételből feladatot gyártani úgy, hogy lerajzoltam az ábrát a hiperbolikus sík egyik jól ismert modelljében, a Poincaré-féle körmodellben.

A Poincaré-féle körmodell²

A hiperbolikus sík modellje azt jelenti, hogy bizonyos dolgokat elnevezünk ,,pontnak'', pontok bizonyos halmazait ,,egyenesnek'', definiáljuk a pontok sorrendjét az egyeneseken, pontok ,,távolságát'' és egyenesek ,,szögét'', és mindezt úgy, hogy az összes geometriai axiómánk teljesüljön, kivéve a párhuzamossági axiómát, ami helyett azt kötjük ki, hogy bármely egyeneshez bármely rajta kívül fekvő pontból végtelen sok párhuzamos egyenest lehet húzni.
Egy korábbi, a KöMaL honlapján is elérhető cikkben [1] összefoglaltam négyféle hiperbolikus modell, a Beltrami‐Cayley‐Klein-modell, a Poincaré-féle kör-, félsík- és félgömbmodellek alapvető definícióit és a modellek közötti megfeleltetéseket. A mostani játékunkhoz csak a körmodell néhány alapvető tulajdonságára lesz szükség.
Vegyünk az euklideszi síkon egy körlapot, ez lesz az ,,alapkör''. A kör belsejébe eső pontok a körmodell pontjai. A körmodell egyenesei az alapkört merőlegesen metsző köröknek az alapkör belsejébe eső ívei, beleértve az alapkör átmérőit is (3. ábra).
Két pont távolságát a következőképpen definiálhatjuk: ha

X

és

Y

két pont az alapkörre merőleges

A B

köríven, akkor az

X

és

Y

pontok távolsága

\begin{matrix} d (X, Y) = k \cdot | ln (A B X Y) | = k \cdot | ln \frac{A X \cdot Y B}{A Y \cdot X B} | . \end{matrix}

(A középső képletben négy, egy körön fekvő pont kettősviszonya szerepel, ami pontosan ugyanúgy fejezhető ki a húrok hosszával, mint amikor egy egyenesre esnek.)
A távolságoknál sokkal szebb a szögek definíciója: két ,,egyenes'' szöge éppen akkora, mint amekkorának a modellben látszik.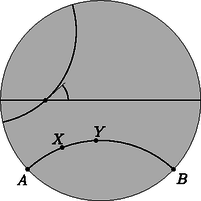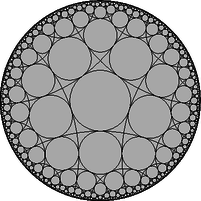

3. ábra

4. ábra

5. ábra

A modellben a tengelyes tükrözések az egyeneseknek megfelelő körívre való inverziók; ennek következménye, hogy a hiperbolikus körvonalak a körmodellben is körvonalnak látszanak. A modell határához közeledve az egyenlő nagyságú köröket a modellben egyre kisebb körökkel kell lerajzolnunk; a 4. ábrán a körmodell egy kicsempézése látható olyan egybevágó szabályos ötszögekkel, amelyek szögei derékszögek, és az ötszögekbe írt köröket is megrajzoltam.
A körmodell csempézéseit rengeteg művészi alkotásban használták már fel; például az 5. ábrán látható Escher³ Circle Limit I című fametszete.

Olimpiai feladatjavaslat

Az 6. ábrán az 1 ábra hiperbolikus változatát rajzoltam le: az

A

pont az alapkör középpontja, az ebből kiinduló

a_{1}

a_{2}

a_{3}

félegyenesek az alapkör sugarai. A

B

pont egy másik pont a modellben, az ebből kiinduló félegyenesek képei az alapkörre merőleges körívek. Az ábrát invertálhatjuk az alapkör határára; a

b_{1}

b_{2}

b_{3}

körívek meghosszabbításai az

B

pont inverzén mennek át, és a modellen kívül megkapjuk az ábra tükörképét is.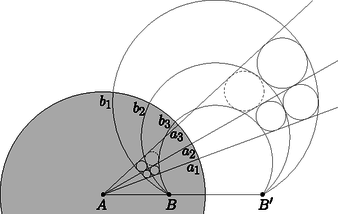

6. ábra

Az ábrával nem voltam elégedett. Túl nyilvánvaló volt, hogyan készült, a tükörkép ábra létrejötte sem tetszett, és a képen szereplő sugarakat és köríveket sem könnyű megrajzolni úgy, hogy metsszék egymást. Azt találtam ki, hogy megváltoztatom a pontok sorrendjét: az

A

pont nem a

B B'

szakasz meghosszabbításán, hanem a belsejében lesz, ettől kezdve az ábra többé már nem a körmodell része. Az alapkör lerajzolására sincs szükség. A pontok cseréje után ez lett az új feladat:

Feladat. A sík

A

és

C

pontjait az

a_{1}

a_{2}

és

a_{3}

körívek úgy kötik össze, hogy az

A C

egyenesnek ugyanazon az oldalán vannak, és az

a_{2}

körív az

a_{1}

és az

a_{3}

között helyezkedik el. Az

A C

szakasz egy

B

pontjából indulnak a

b_{1}

b_{2}

és

b_{3}

félegyenesek, ugyanabban a félsíkban, mint a körívek; a

b_{2}

félegyenes

b_{1}

és

b_{3}

között helyezkedik el.
Tekintsük a körívek és félegyenesek által határolt, négyoldalú

a_{1} b_{1} a_{2} b_{2}

a_{1} b_{2} a_{2} b_{3}

a_{2} b_{1} a_{3} b_{2}

, és

a_{2} b_{2} a_{3} b_{3}

tartományokat. Bizonyítsuk be, hogy ha ezek közül valamelyik háromba kört lehet írni, akkor a negyedikbe is (7. ábra).

7. ábra

A feladatot (kicsit más betűzéssel) javasoltuk a 2010-es, Nemzetközi Matematikai Diákolimpiára, amelyet Kazahsztán új fővárosában, Asztanában rendeztek.
A pontok átrendezése miatt az eredeti, hiperbolikus geometriai megoldás már nem működik, de egy feladatjavaslathoz egyébként is illik elemi megoldásokat mellékelni. Két megoldást mutatok.

1. megoldás, kúpokkal

A kiinduló feladat mintájára, az ábrában szereplő körökre egymáshoz hasonló kúpokat fogunk illeszteni, majd megszerkesztjük a negyedik kúpot. A változás az, hogy most olyan körök is szerepelnek, amelyek két rögzített körív ,,közé'' vannak írva. Megvizsgáljuk, hol lehetnek, milyen pályán mozoghatnak az ilyen körök középpontjai, és a körökre illesztett kúpok csúcsai.

1. lemma. Azoknak a köröknek a középpontjai, amelyek kívülről érintik

a_{i}

-t és belülről érintik

a_{i + 1}

-et, egy,

A

-t és

C

-t összekötő ellipszisíven vannak.

(i = 1

vagy

i = 2.)

Bizonyítás. Feltehetjük, hogy

i = 1

.
Legyen

k

olyan kör, amely kívülről érinti

a_{1}

-et és belülről érinti

a_{2}

-t, az érintési pontjai az

a_{1}

íven

T

, az

a_{2}

íven

U

, a középpontja

P

. Legyen az

a_{1}

kör középpontja

O_{1}

, az

a_{2}

középpontja

O_{2}

, a körök sugarai

r

r_{1}

, illetve

r_{2}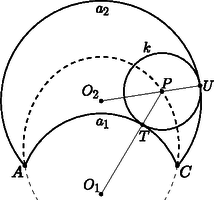

(8. ábra).

8. ábra

Vegyük észre, hogy

\begin{matrix} O_{1} P + O_{2} P = (O_{1} T + T P) + (O_{2} U - P U) = (r_{1} + r) + (r_{2} - r) = r_{1} + r_{2}, \end{matrix}

vagyis

P

rajta van az

O_{1}, O_{2}

fókuszú,

r_{1} + r_{2}

nagytengelyű ellipszisen; ez az ellipszis átmegy az

A

és

C

pontokon, mert

O_{1} A + O_{2} A = O_{1} C + O_{2} C = r_{1} + r_{2}

.
Megfordítva, ha

P

egy pont az ellipszisnek az

a_{1}

és

a_{2}

közötti ívén, akkor a

P

középpontú,

r = O_{1} P - r_{1} = r_{2} - O_{2} P

sugarú kör kívülről érinti

a_{1}

-et és belülről érinti

a_{2}

-t.

2. lemma. Legyen

φ

rögzített hegyesszög, és

i = 1

vagy

i = 2

. Tekintsük azokat a köröket, amelyek kívülről érintik

a_{i}

-t és belülről érintik

a_{i + 1}

-et, és emeljünk ezekre felfelé ezekre a körökre olyan kúpokat, amelyek alkotói

φ

szöget zárnak be a

Σ

síkkal. Az így kapható kúpok csúcsai egy,

A

-t és

C

-t összekötő ellipszisíven vannak.

Bizonyítás. Ismét feltesszük, hogy

i = 1

. Illesszünk az

a_{1}

körre lefelé, az

a_{2}

-re felfelé egy-egy kúppalástot, amelyek alkotói

φ

szöget zárnak be

Σ

-val; ezek csúcsa legyen

P

, illetve

Q

.
Legyen

k

egy tetszőleges kör, amely kívülről érinti

a_{1}

-et és belülről érinti

a_{2}

-t, a középpontja

O

, az érintési pontjai az

a_{1}

íven

T

, az

a_{2}

íven

U

. A

k

-ra felfelé illesztett kúp csúcsa legyen

K

. (9. ábr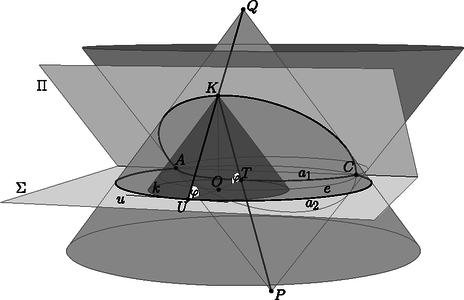a).

9. ábra

Legyen

u

k

és az

a_{2}

ív

U

-ban húzott közös érintője. Az

U K

félegyenes a

k

-ra emelt kúp, az

U Q

félegyenes pedig az

a_{2}

-re emelt kúp alkotója. Mindkettő merőleges

u

-ra,

φ

szöget zár be

Σ

-val, és a körök belseje felé dől, ezért a két félegyenes ugyanaz. Tehát a

K

pont rajta van az

U Q

egyenesen, és ezáltal az

a_{2}

ívre illesztett kúpon.
Ugyanígy láthatjuk, hogy a

T K

félegyenes a

k

-ra illesztett kúp, a

T P

félegyenes az

a_{1}

-re lefelé illesztett kúp alkotója, és ezek egymás meghosszabbításai, így a

K

pont az

a_{1}

-re illesztett kúppaláston is rajta van, tehát

K

közös pontja az

a_{1}

-re és az

a_{2}

-re illesztett kúppalástoknak.
A cikk 3. részében láttuk, hogy párhuzamos tengelyű, azonos meredekségű kúpok közös pontjai egy síkban vannak. Tehát a lehetséges

K

pontok egy rögzített

Π

síkban vannak. A két kúpnak

A

és

C

is közös pontja, tehát a

Π

sík illeszkedik az

A C

egyenesre.
Az 1. lemma szerint a lehetséges

O

pontok egy

e

ellipszisívet alkotnak, amely összeköti

A

-t és

C

-t. Ha ezt az ellipszist

Σ

-ra merőlegesen visszavetítjük

Π

-re, megkapjuk a lehetséges

K

pontokat tartalmazó ellipszisívet a

Π

síkban.

Most térjünk rá a feladat megoldására. A 2. lemma szerint az

a_{i}

és

a_{i + 1}

ívek közé írt körökre emelt kúpok csúcsai egy

A

-t és

C

-t összekötő

c_{i}

ellipszisíven vannak

(i = 1,2)

. A

b_{j}

és

b_{j + 1}

ívek közé írt körökhöz tartozó kúpok csúcsai pedig egy

B

-ből induló

d_{j}

egyenesen (

j = 1,2

).
Legyen

P

Q

és

R

a_{1} b_{1} a_{2} b_{2}

, az

a_{1} b_{2} a_{2} b_{3}

, illetve az

a_{2} b_{1} a_{3} b_{2}

tartományokba írt körre emelt kúp csúcsa; ekkor

P

c_{1}

és

d_{1}

metszéspontja,

Q

c_{1}

és

d_{2}

metszéspontja, és

R

c_{2}

és

d_{1}

metszéspontja. A feladat megoldásához elég azt igazolnunk, hogy

c_{2}

és

d_{2}

is elmetszi egymást (10. ábra).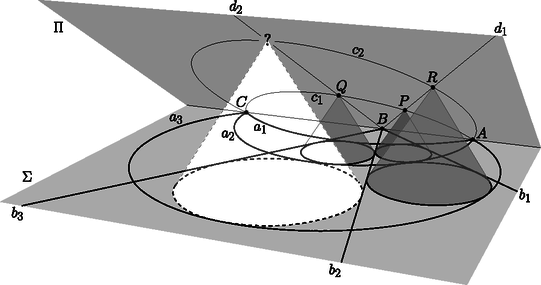

10. ábra

Legyen

Π

az a félsík, aminek határa az

A C

egyenes, és illeszkedik a

B P R

félegyenesre. Ez a félsík tartalmazza a

c_{1}

és

c_{2}

ellipszisíveknek három-három pontját (

A

C

P

, illetve

A

C

R

), így mindkét ellipszisív része

Π

-nek. Mivel

c_{1}

átmegy

Q

-n, a

Q

pont és a

d_{2}

félegyenes is része

Π

-nek. A

c_{2}

ellipszisnek

B

belső pontja, ezért a

B Q

félegyenes elmetszi

c_{2}

-t. Ezzel a feladatot megoldottuk.

2. megoldás, térbe kilépés nélkül

Az előbbi megoldást nem nehéz tisztán síkbeli bizonyítássá alakítani. Az 1. lemmára most is szükségünk lesz.

3. lemma. Válasszunk egy tetszőleges

k

kört, amely kívülről érinti

a_{i}

-t és belülről érint

a_{i + 1}

-et

(i = 1

vagy

i = 2)

, a középpontja

O

, sugara

r

, és legyen

d

O

pont és az

A C

egyenes távolsága. Az

r / d

arány nem függ a

k

megválasztásától.

Nem nehéz észrevenni, hogy a 3. lemma a 2. lemma egyszerű átfogalmazása.

Bizonyítás. Az 1. lemmához hasonlóan legyen

i = 1

, az

a_{1}

középpontja

O_{1}

, az

a_{2}

középpontja

O_{2}

. Legyenek

k

és

k'

különböző körök, amik érintik a két ívet, sugaraik

r

, illetve

r'

; középpontjaik

O

, illetve

O'

, távolságuk az

A C

egyenestől

d

, illetve

d'

. Azt akarjuk igazolni, hogy

\frac{r}{d} = \frac{r'}{d'}

.
Ha

k

és

k'

szimmetrikus az

O_{1} O_{2}

egyenesre, akkor az állítás triviális; feltehetjük, hogy a két kör nem egymás tükörképe. A két kör érintési pontja a két köríven legyen

T

T'

U

és

U'

a 11. ábra szerint.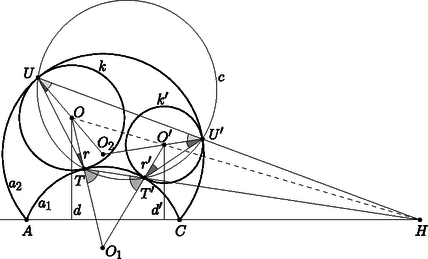

11. ábra

Legyen a

k

és

k'

körök külső hasonlósági pontja

H

. A

k

és az

a_{2}

külső hasonlósági pontja

U

, a

k'

és az

a_{2}

külső hasonlósági pontja

U'

; a Monge-tétel szerint a három hasonlósági pont,

H

U

és

U'

egy egyenesen van. Hasonlóan, a

k

és az

a_{1}

belső hasonlósági pontja

T

, a

k'

és az

a_{1}

belső hasonlósági pontja

T'

; a Monge-tétel szerint

H

T

és

T'

is egy egyenesen van. A

H

pont tehát a

T T'

és az

U U'

egyenes metszéspontja.
A

T T' U' U

négyszög szemközti szögeinek összegét összeszámolhatjuk az

O U T

O_{1} T T'

O' T' U'

és

O_{2} U' U

egyenlő szárú háromszögekből, és láthatjuk, hogy a szögek összege két szemközti csúcspárnál ugyanakkora; tehát a

T T' U' U

négyszög húrnégyszög. (A háromszögek irányításától függően az ábra többféleképpen is kinézhet, ezért a teljes bizonyításhoz többféle esetet is meg kell vizsgálni.) Az

a_{1}

és a

T T' U U'

kör hatványvonala a

T T'

egyenes, az

a_{2}

és a

T T' U U'

kör hatványvonala pedig az

U U'

egyenes, tehát

H

a három kör hatványpontja, és ezen a harmadik hatványvonal, az

A C

egyenes is átmegy.
A

k

és

k'

köröket, sugaraikat és a

d

d'

távolságokat egymásba nagyíthatjuk a

H

pontból, ez bizonyítja, hogy

\frac{r}{d} = \frac{r'}{d'}

Az 1. és a 3. lemma együtt megoldja a feladatot. Tegyük fel, hogy az

a_{1} b_{1} a_{2} b_{2}

a_{1} b_{2} a_{2} b_{3}

és

a_{2} b_{1} a_{3} b_{2}

tartományokba kört lehet írni; ezt a három kört jelölje rendre

k_{1}

k_{2}

, illetve

k_{3}

. Sugaraik legyenek

r_{1}

r_{2}

, illetve

r_{3}

; középpontjaik távolsága az

A C

egyenestől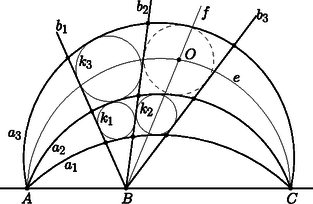

d_{1}

d_{2}

, illetve

d_{3}

12. ábra

Legyen

e

az az 1. lemma szerinti ellipszisív, amely az

a_{2}

és

a_{3}

köríveket érintő körök középpontjaiból áll, és legyen

f

b_{2}, b_{3}

félegyenesek szögfelezője; az

e

és az

f

metszéspontja legyen

O

, az

O

távolsága az

A C

egyenestől

d

(12. ábra).
A 3. lemma szerint

\frac{r_{1}}{d_{1}} = \frac{r_{2}}{d_{2}}

, továbbá a

k_{1}

és

k_{3}

köröket a

B

pontból egymásba lehet nagyítani, ezért

\frac{r_{1}}{d_{1}} = \frac{r_{3}}{d_{3}}

. Legyen

r = \frac{r_{2}}{d_{2}} \cdot d = \frac{r_{3}}{d_{3}} \cdot d

. A 3. lemma szerint az

O

középpontú,

r

sugarú kör érinti az

a_{2}

és az

a_{3}

ívet is. Továbbá, a

k_{2}

kört a

B

pontból ugyanebbe a körbe nagyíthatjuk. Ezzel megszerkesztettük az

a_{2} b_{2} a_{3} b_{3}

tartomány beírt körét.

Asztanai közjáték

Asztanába megérkezve az a meglepetés ért, hogy az olimpia helyszínén létezik egy épület (a neve Shabyt), ami két párhuzamos tengelyű kúp metszete. A feladatkiválasztó bizottság tagjaival készítettünk is néhány fényképet rólam és a feladatomról.

A ,,Shabyt'' (,,

'', jelentése: inspiráció

)

művészeti egyetem Asztanában,
Kazahsztán fővárosában

A zsűriben a feladat nem volt annyira népszerű. Többeknek tetszett, de a térgeometriától ódzkodó csendes többség gyorsan kiszavazta a lehetséges nehéz jelöltek közül. (De azért nem ez volt a legnépszerűtlenebb feladat: a C6-os feladatot még ennél is jobban utálták.)
Az olimpia megnyitó ünnepsége a Függetlenségi Palotában volt, közvetlenül a Shabyt melletti épületben. A zsűri nagy része a megnyitóra utazás közben, a buszról látta először az épületet, amikor már rég kiválasztották a hat feladatot a versenyre.

Feladatok

1. Oldjuk meg a Kiinduló feladatot a körökhöz húzott érintő szakaszok összehasonlításával.

2. Bizonyítsuk be a 2. lemmát úgy, hogy az

a_{1}

és

a_{2}

körívekre nem kúpokat, hanem olyan gömböket illesztünk, amelyek

φ

szögben metszik a

Σ

síkot.

3. Bizonyítsuk be a 3. lemmát koordinátákkal.

4. Mutassuk meg, hogy a 7. ábrát inverzióval egy félgömbfelületre képezhetjük úgy, hogy az

a_{1}

a_{2}

a_{3}

b_{1}

b_{2}

b_{3}

görbék képei a gömbön fél főkörök legyenek (13. ábra). Az így kapott gömbi állítást bizonyítsuk be a békaszem-módszerrel.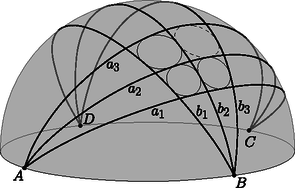

13. ábra

Irodalom

[1]	Kós Géza: Hiperbolikus Escher-grafikák. KöMaL 55/1 (2005. január), 2‐10. https://www.komal.hu/cikkek/2005-01/escher.h.shtml

[2]	G7 feladat. IMO Shortlist 2010, 60‐63. https://www.imo-official.org/problems/IMO2010SL.pdf

¹A cikksorozat a Rényi Intézet és a Sztaki támogatásával készült.

²Jules Henri Poincaré francia matematikus, 1854‐1912

³Maurits Cornelis Escher holland grafikus, 1898‐1972.