Cím:	A 2019. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldásai
Szerző(k):	Pach Péter Pál
Füzet:	2020/február, 67 - 71. oldal	PDF  |  MathML
Témakör(ök):	Matematika, Kürschák József (korábban Eötvös Loránd), Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   1. Az $ABC$ hegyesszögű háromszögben $AB<AC<BC$, az $A$, $B$, $C$ csúcsokból induló magasságok talppontjai rendre $A_1$, $B_1$, illetve $C_1$. Legyen $P$ a $C_1$ pont tükörképe a $B{B}_1$ egyenesre, és legyen $Q$ a $B_1$ pont tükörképe a $C{C}_1$ egyenesre. Mutassuk meg, hogy az $A_{1}PQ$ háromszög köré írt kör átmegy a $BC$ oldal felezőpontján.     Megoldás. Először megmutatjuk, hogy a $P$ pont az $A_1{B}_1$, a $Q$ pedig az $A_1{C}_1$ szakasznak belső pontja. Legyen $A\text{'}$ az $A$ csúcsnak a $B{B}_1$ magasságra vonatkozó tükörképe. Az $AB<BC$ feltétel miatt $A{B}_1<B_{1}C$, ezért az $A\text{'}$ pont a $B_{1}C$ szakasznak belső pontja. A $BA\text{'}$ szakasz a háromszög belsejében halad, és $P$ ennek belső pontja, tehát $P$ a háromszög belsejébe esik. Jól ismert, hogy bármely hegyesszögű háromszögben a magasságvonalak felezik a talpponti háromszög szögeit, ezért a $B_1{C}_1$ félegyenesnek a $B{B}_1$ magasságra vonatkozó tükörképe a $B_1{A}_1$ félegyenes. A $P$ pont tehát a $B_1{A}_1$ félegyenesnek a háromszög belsejébe eső szakaszán, vagyis az $A_1{B}_1$ szakasz belsejében helyezkedik el. Hasonlóan láthatjuk, hogy $AC<BC$ miatt $Q$ az $A_1{C}_1$ szakasznak belső pontja. 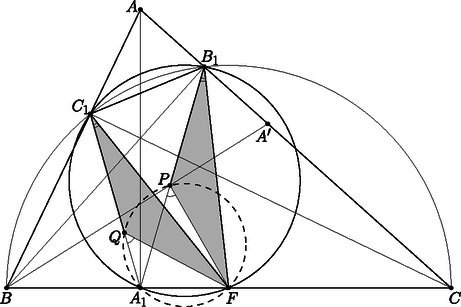    Legyen $BC$ felezőpontja $F$; az $F{B}_1$ és $F{C}_1$ szakaszok a $BC$ oldal Thalész-körének sugarai, ezért $F{B}_1=F{C}_1$. Szintén jól ismert, hogy az $A_1$, $B_1$, $C_1\mathrm{,}F$ pontok egy körön, a háromszög Feuerbach-körén vannak. Vegyük észre, hogy az $F{B}_{1}P$ és $F{C}_{1}Q$ háromszögek egybevágók, mert $F{B}_1=F{C}_1$, $B_{1}P=B_1{C}_1=C_{1}Q$, és $P{B}_{1}F\sphericalangle =A_1{B}_{1}F\sphericalangle =A_1{C}_{1}F\sphericalangle =Q{C}_{1}F\sphericalangle$ az $A_1{B}_{1}F$ ívhez tartozó kerületi szögek a Feuerbach-körön. Tehát $\begin{array}{c}{\displaystyle A_{1}PF\sphericalangle ={180}^{\circ }-FP{B}_1\sphericalangle ={180}^{\circ }-FQ{C}_1\sphericalangle =A_{1}QF\sphericalangle \mathrm{,}}\end{array}$ ez pedig mutatja, hogy az $A_1$, $F$, $P$, $Q$ pontok egy körön vannak, ahogy az bizonyítandó volt.  $\square$   2. Legyen $n$ pozitív egész szám. Határozzuk meg az összes olyan $\text{F}$ halmazrendszert, amely az $\left\{\mathrm{1,2,}\text{...}\mathrm{,}n\right\}$ halmaz bizonyos részhalmazaiból áll, és amelyre minden rögzített, nemüres $X\subseteq \left\{\mathrm{1,2,}\text{...}\mathrm{,}n\right\}$ mellett ugyanannyi $A\in \text{F}$ esetén lesz $A\cap X$ elemszáma páros, mint páratlan.     I. megoldás. Számoljuk meg kétféleképpen, hogy hány olyan $\left(A\mathrm{,}B\mathrm{,}C\right)$ rendezett hármas van, melyre $A$ és $B$ az $\text{F}$ halmazrendszer két különböző eleme, $C\subseteq \left\{\mathrm{1,2,}\text{...}\mathrm{,}n\right\}$ pedig egy olyan nemüres részhalmaz, melyre az $A\cap C$ és $B\cap C$ halmazok elemszámának paritása különbözik. $\left(*\right)$ Először is megjegyezzük, hogy bármely (véges) nemüres $S$ halmaz részhalmazainak pontosan a fele páros, illetve páratlan méretű. Sőt, általánosabban, ha $T\supseteq S$ egy (véges) halmaz, akkor $T$ részhalmazainak éppen a fele metszi (a nemüres) $S$-et páros, illetve páratlan elemszámú halmazban (hiszen $S$ minden részhalmaza ugyanannyiféleképpen, $2^{|T\setminus S|}$-féleképpen, egészíthető ki $T$ részhalmazává). Ezt az észrevételt a megoldás során többször is fel fogjuk használni. Legyen $|\text{F}|=t$. Először $A$ és $B$ megválasztásával kezdjük: $A$-ra $t$ lehetőség van, ezután $B$-re $\left(t-1\right)$, hiszen $A\ne B\in \text{F}$. Ezután pontosan azok a $C$ nemüres halmazok megfelelők, melyek az $A\Delta B$ (nemüres) halmazt (vagyis $A$ és $B$ szimmetrikus differenciáját) páratlan sok elemben metszik. Ezt a feltételt $\left(*\right)$ alapján a részhalmazok fele teljesíti (és nincs köztük az $\varnothing$), így a megfelelő $C$ halmazok száma $2^{n-1}$. Tehát a megfelelő $\left(A\mathrm{,}B\mathrm{,}C\right)$ hármasok száma $t\left(t-1\right)2^{n-1}$. Most ugyanezt másféleképpen is megszámoljuk: először $C$-t választjuk meg, erre ($2^n-1$)-féle lehetőség van. Ezután az olyan $\left(A\mathrm{,}B\right)$ párok lesznek megfelelők, melyekre $|A\cap C|$ és $|B\cap C|$ paritása különböző. Az $A\in \text{F}$ halmaz tetszőlegesen megválasztható, majd ezután a feltétel szerint éppen $t/2$ esetben lesz $|B\cap C|$ paritása megfelelő (vagyis $|A\cap C|$ paritásától különböző). Így a hármasok száma $\left(2^n-1\right)t\left(t/2\right)$. A $t\left(t-1\right)2^{n-1}=\left(2^n-1\right)t\left(t/2\right)$ ($t$-ben másodfokú) egyenlet megoldásai $t=0$ és $t=2^n$. Tehát az üres halmazon és az összes részhalmazt tartalmazó halmazrendszeren kívül nincs megfelelő $\text{F}$. Ez a két halmazrendszer pedig teljesíti a feltételeket: ha $\text{F}$ az üres halmazrendszer, akkor $A\cap X$ elemszáma 0-szor lesz páros, 0-szor lesz páratlan; ha pedig $\text{F}$ az összes részhalmazt tartalmazó halmazrendszer, akkor $\left(*\right)$ szerint bármely nemüres $X$-re $A\cap X$ elemszáma $2^{n-1}$ esetben páros, $2^{n-1}$ esetben páratlan. Tehát két megfelelő halmazrendszer van: az üres halmaz és az $\left\{\mathrm{1,2,}\text{...}\mathrm{,}n\right\}$ összes részhalmazát tartalmazó halmazrendszer.  $\square$     II. megoldás (Fleiner Zsigmond és Velich Nóra megoldása alapján). Megmutatjuk, hogy csak az üres halmazrendszer és az összes részhalmazt tartalmazó halmazrendszer megfelelő. Legyen ismét $|\text{F}|=t$. Készítsünk egy $t\times 2^n$ méretű táblázatot, melynek sorai az $\text{F}$-beli halmazoknak, oszlopai pedig az $\left\{\mathrm{1,2,}\text{...}\mathrm{,}n\right\}$ részhalmazainak felelnek meg. Bármely $A\in \text{F}$ és $X\subset \left\{\mathrm{1,2,}\text{...}\mathrm{,}n\right\}$ halmazok esetén az $A$-nak megfelelő sor és az $X$-nek megfelelő oszlop közös mezőjébe írjunk $\left(+1\right)$-et, ha $|A\cap X|$ páros, illetve $\left(-1\right)$-et, ha $|A\cap X|$ páratlan. Ebben a táblázatban számítsuk ki a számok összegét kétféleképpen: oszloponként és soronként is. A feltétel szerint bármely nemüres $X$ esetén az $A\in \text{F}$ halmazoknak pontosan a felére lesz $|A\cap X|$ páros, illetve páratlan, vagyis az $X$-nek megfelelő oszlopban a számok fele $+1$, fele $-1$; az összegük $0$. Az üres halmaz minden $A\in \text{F}$-et a páros üres halmazban metsz, tehát az üres halmaznak megfelelő oszlopban mind a $t$ elem $+1$. Azt kaptuk, hogy a táblázatban az elemek összege $t$. Ha $\varnothing \in \text{F}$, akkor az $\varnothing$-nak megfelelő sorban csupa $+1$ áll, ezek összege $2^n$. Tekintsünk most egy tetszőleges nemüres $A\in \text{F}$ elemet és a neki megfelelő sort. Mivel az $A$ nemüres, az $\left\{\mathrm{1,2,}\text{...}\mathrm{,}n\right\}$ részhalmazaival vett metszeteinek éppen a fele páros, iletve páratlan; az ilyen sorokban az elemek összege $0$. Összességében, a táblázat összege $2^n$, ha $\varnothing \in \text{F}$, és $0$, ha $\varnothing \notin \text{F}$. A kétféle összeszámolásból azt kaptuk, hogy $t=0$ vagy $t=2^n$, vagyis $\text{F}$ az üres halmazrendszer, vagy pedig $\left\{\mathrm{1,2,}\text{...}\mathrm{,}n\right\}$ összes részhalmazából áll. Azt, hogy ez a két halmazrendszer teljesíti a feltételeket, ugyanúgy ellenőrizhetjük, mint az I. megoldásban.  $\square$   3. Igaz-e, hogy ha $H$ és $A$ a számegyenes korlátos részhalmazai, akkor $H$ legfeljebb egyféleképpen bontható fel $A$ páronként diszjunkt eltolt példányaira? (Végtelen sok eltolt példányt is megengedünk.)     I. megoldás. Megmutatjuk, hogy a kérdéses következtetés nem igaz. Rekurzívan felépítjük $A$-t, $H$-t, és az $E\ne E\text{'}$ eltoláshalmazokat (mind $\text{R}$ nemüres részhalmazai), úgy, hogy $\begin{array}{c}{\displaystyle H=\bigcup _{e\in E}^{}\left(A+e\right)=\bigcup _{e\text{'}\in E\text{'}}^{}\left(A+e\text{'}\right)\mathrm{,}}\end{array}$ és mind az $A+e=\left\{a+e:a\in A\right\}$ ($e\in E$) eltoltak, mind az $A+e\text{'}=\left\{a+e\text{'}:a\in A\right\}$ ($e\text{'}\in E\text{'}$) eltoltak páronként diszjunktak. Legyen először $A_1=\left\{0\right\}$, $E_1=\left\{0\right\}$, $E{\text{'}}_1=\left\{1\right\}$, és $H_1=\left(A_1+E_1\right)\cup \left(A_1+E{\text{'}}_1\right)=\left\{\mathrm{0,1}\right\}$. Innen rekurzívan haladunk tovább. Tegyük fel, hogy már megkonstruáltuk a véges $A_n$, $E_n$, $E{\text{'}}_n$ halmazokat úgy, hogy $E_n\cap E{\text{'}}_n=\varnothing$, $A_n+E_n$ és $A_n+E{\text{'}}_n$ minden általuk lefedett elemet egyszer fednek (vagyis az $A+e$ $\left(e\in E_n\right)$ halmazok páronként diszjunktak, és az $A+e\text{'}$ $\left(e\text{'}\in E_n\text{'}\right)$ halmazok is páronként diszjunktak). Legyen ekkor $H_n=\left(A_n+E_n\right)\cup \left(A_n+E{\text{'}}_n\right)$. Most egymás után minden egyes $h\in H_n$ elemre a következőt tesszük: ha $h$ eddig nem volt benne $A_n+E_n$-ben, akkor beteszünk $A_n$-be egy $a$, $E_n$-be egy $e$ elemet, hogy azok összege éppen $h$ legyen, és a korábbi tulajdonságok ne romoljanak el, azaz $a$ ne legyen $a_1+e_1-e_2$ alakú (ahol ezek korábbi elemek: $a_1\in A_n$, $e_1\mathrm{,}{e}_2\in E_n$), és $e$ se legyen $e_1+a_1-a_2$ alakú (ahol $e_1\in E_n$, $a_1\mathrm{,}{a}_2\in A_n$), sőt, az új $e$ ne legyen $E{\text{'}}_n$-ben sem. Mindegyik feltétel véges sok elem letiltását jelenti. Ugyanígy járunk el $A_n+E{\text{'}}_n$ esetében is. Így kapjuk az $A_{n+1}\mathrm{,}{E}_{n+1}\mathrm{,}E{\text{'}}_{n+1}$ halmazokat, nyilván $H_n\subseteq A_{n+1}+E_{n+1}$, $H_n\subseteq A_{n+1}+E{\text{'}}_{n+1}$. Világos, hogy $A=\bigcup _{n=1}^{\infty }{A}_n$, $E=\bigcup _{n=1}^{\infty }{E}_n$, $E\text{'}=\bigcup _{n=1}^{\infty }E{\text{'}}_n$, $H={\bigcup }_{n=1}^{\infty }{H}_n$ megfelelnek, amennyiben a korlátosság is teljesül. Azonban a korlátosságot is könnyen betarthatjuk, ha minden új elemet a $\left(-\mathrm{2,2}\right)$ intervallumból választunk a következőképpen: egy tipikus lépésben egy adott $H_n\ni h\in \left(-\mathrm{2,2}\right)+\left(-\mathrm{2,2}\right)=\left(-\mathrm{4,4}\right)$ elemet akarunk felírni $a+e$ alakban, ahol $a\in A_{n+1}$, és $e\in E_{n+1}$ (vagy $E_{n+1}\text{'}$). Világos, hogy mivel csak véges sok letiltott elem van, léteznek ennek megfelelő $a\mathrm{,}e\in \left(-\mathrm{2,2}\right)$ számok.  $\square$     II. megoldás (Matolcsi Dávid dolgozata alapján). Legyen $H$ a $\left(-\mathrm{2,2}\right)$ nyílt intervallumba eső, 3-hatvány nevezőjű racionális számok halmaza. Legyen $A\subset \left(-\mathrm{1,1}\right)$ a $\pm \left(1-3^{-r}\right)$ alakú számok halmaza, ahol $r$ nemnegatív egész. Be fogjuk látni, hogy $H$ többféleképpen is felbontható $A$-nak páronként diszjunkt eltoltjaira. Legyen $E$ a $\left[-\mathrm{1,1}\right]$ zárt intervallumba eső, 3-hatvány nevezőjű racionális számok halmaza. Ekkor $A+E=\{a+e:a\in A$, $e\in E\}\subseteq H$ (itt valójában egyenlőség áll). Mivel $A$ és $A+2/3$ is tartalmazza a $2/3$ számot, ezért $A$-nak ez a két eltoltja nem diszjunkt. Elég belátni, hogy mindkettő kiegészíthető $H$ felbontásává $A$-nak páronként diszjunkt eltoltjaira. Mivel $H$ megszámlálható, elég belátni, hogy ha valamely $e_1\mathrm{,}\text{...}\mathrm{,}{e}_n\in E$ számokkal képzett $A+e_i$ eltoltak nem tartalmazzák a $h\in H$ számot, akkor van olyan $e\in E$ szám, hogy az $A+e$ eltolt tartalmazza a $h$ számot és diszjunkt $A+e_1\mathrm{,}\text{...}\mathrm{,}A+e_n$ mindegyikétől. Válasszuk az $r\ge 2$ egész számot olyan nagynak, hogy $3^{r-2}\left(h-e_i\right)$ egész legyen minden $i=\mathrm{1,}\text{...}\mathrm{,}n$ esetén, továbbá $3^{-r}\le 2-|h|$ álljon. Ekkor $|h|-\left(1-3^{-r}\right)\le 1$, tehát tudunk olyan előjelet választani, hogy az $a=\pm \left(1-3^{-r}\right)$ és $e=h-a$ választással $|e|\le 1$, azaz $e\in E$ legyen. Ekkor $h=a+e\in A+e$. Már csak azt kell belátnunk, hogy $b\mathrm{,}c\in A$ és $1\le i\le n$ esetén $b+e\ne c+e_i$, azaz $b+h-a\ne c+e_i$, vagyis $a-b+c\ne h-e_i$. Mivel $h\notin A+e_i$, ezért $h-e_i\notin A$, tehát $a=b$ vagy $a=-c$ esetén készen vagyunk, hiszen ekkor $a-b+c\in A$. (Utóbbi esetben használjuk, hogy az $A$ halmaz a 0-ra szimmetrikus.) Egyéb esetben belátjuk, hogy $3^{r-2}\left(a-b+c\right)$ nem egész, amiből a kívánt nem-egyenlőség azonnal következik. Legyen $b=\pm \left(1-3^{-s}\right)$ és $c=\pm \left(1-3^{-t}\right)$, ekkor $3^r\left(a-b+c\right)=\pm \left(3^r-1\right)\mp \left(3^r-3^{r-s}\right)\pm \left(3^r-3^{r-t}\right)$, ahol $3^r$ egy 9-cel osztható egész, $\mp 1\pm 3^{r-s}\mp 3^{r-t}$ pedig nem, mert $\underset{}{\overset{}{\text{max}}}\left(s\mathrm{,}t\right)>r$ esetén ez vagy $\mp 1$, vagy nem egész, $\underset{}{\overset{}{\text{max}}}\left(s\mathrm{,}t\right)\le r$ esetén pedig vagy $\mp 3$, vagy nem osztható 3-mal. Így tehát $3^r\left(a-b+c\right)$ nem lehet 9-cel osztható egész.  $\square$