Cím:	Megoldásvázlatok a 2019/98. szám emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Koncz Levente (Budapest)
Füzet:	2020/január, 13 - 24. oldal	PDF  |  MathML
Témakör(ök):	Cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Hány olyan négyjegyű pozitív egész szám van, amelyben a számjegyek összege legfeljebb $4?$  (7 pont) $b)$ Hány olyan lesz ezek között a számok között, amely osztható $60$-nal?   (5 pont)   Megoldás. $a)$ A sorrendre való tekintet nélkül 11-féleképpen tudjuk előállítani a 4-et, a 3-at, a 2-t vagy az 1-et négy nemnegatív egész szám összegeként: $4=4+0+0+0=3+1+0+0=2+2+0+0=2+1+1+0=1+1+1+1$ (5 lehetőség); $3=3+0+0+0=2+1+0+0=1+1+1+0$ (3 lehetőség); $2=2+0+0+0=1+1+0+0$ (2 lehetőség); $1=1+0+0+0$ (1 lehetőség). Az $X000$ típusból csak egyféleképpen alkothatunk négyjegyű számot, mert a 0 nem állhat a legnagyobb helyiértéken. Az $XY00$ típusban 3-féleképpen választhatjuk ki a két nulla helyét, a maradék két helyre 2-féleképpen variálhatjuk a másik két számjegyet, tehát ezekből egyaránt $\left(3\cdot 2=\right)6$ négyjegyű számot képezhetünk. Az $XX00$ típusban 3-féleképpen választhatjuk ki a két nulla helyét, így ezekből 3 különböző négyjegyű szám adódik. Az $XYY0$ típusban 3-féleképpen választhatjuk ki a nulla helyét, ezután 3-féleképpen választhatjuk ki az $X$ helyét, így ebből $\left(3\cdot 3=\right)9$-féle négyjegyű szám képezhető. Az $XXX0$ típusban 3-féleképpen választhatjuk ki a nulla helyét, így ebből 3 különböző négyjegyű szám adódik. Végül az $XXXX$ típusból csak egyféleképpen alkothatunk négyjegyű számot. Összesen tehát $\left(1+6+3+9+1+1+6+3+1+3+1=\right)35$, a feltételeknek megfelelő négyjegyű szám van.   $b)$ 60-nal pontosan akkor osztható egy szám, ha 3-mal, 4-gyel, és 5-tel is osztható. 3-mal csak akkor osztható a szám, ha számjegyeinek összege 3-mal osztható, tehát esetünkben a számjegyek összege 3. 5-tel akkor osztható, ha 0-ra vagy 5-re végződik, de 5-re végződő szám nincs a szóba jövő számok között, a számnak tehát 0-ra kell végződnie. 4-gyel akkor osztható, ha az utolsó két számjegyéből képzett szám osztható 4-gyel, tehát a szóba jöhető lehetőségek közül az utolsó két számjegy 00 vagy 20 lehet (12 nem lehet, mert az 5-tel oszthatóság miatt 0-ra kell végződnie). Azok a négyjegyű számok, melyek 00-ra vagy 20-ra végződnek, és számjegyeik összege 3, a következők: 3000, 2100, 1200, 1020. Tehát 4, a feltételeknek megfelelő szám van.   2. $a)$ Egy osztályban egy matematika dolgozatnál a $6$ kékszemű tanuló átlaga pontosan $3$, a többi, nem kékszemű tanuló átlaga pontosan $4$ lett. A $21$ fiú átlaga pontosan $3\mathrm{,}5$, a lányok átlaga pontosan $4\mathrm{,}5$ lett. Határozzuk meg a dolgozat átlagát a teljes osztályban.  (5 pont) $b)$ Az iskolai túraszakosztály a hétvégi kirándulásra különbuszt rendelt. A buszköltséget a résztvevők között egyenlő arányban osztják szét. A kitűzött jelentkezési határidő egy hétfői napon járt le. Mivel maradt még szabad hely a buszban, ezért kedden még két jelentkezést elfogadtak, így az egy résztvevőre jutó buszköltség 175 Ft-tal csökkent. Szerdán aztán még három jelentkezést elfogadtak, így az egy résztvevőre jutó buszköltség további 225 Ft-tal csökkent. Így már megtelt a megrendelt autóbusz.   Hány jelentkezést fogadtak el összesen a kirándulásra, és mennyibe került a megrendelt különbusz?  (8 pont)   Megoldás. $a)$ Jelölje az osztály létszámát $x$. Az osztályzatok összegét kétféleképpen felírva: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 6\cdot 3+\left(x-6\right)\cdot 4}& {\displaystyle =21\cdot 3\mathrm{,}5+\left(x-21\right)\cdot 4\mathrm{,}\mathrm{5,}}\hfill \\ \hfill {\displaystyle 4x-6}& {\displaystyle =4\mathrm{,}5x-\mathrm{21,}}\hfill \\ \hfill {\displaystyle x}& {\displaystyle =30.}\hfill \end{array}}$ Az osztály létszáma 30 volt. A dolgozat átlaga a teljes osztályban $\frac{6\cdot 3+24\cdot 4}{30}=3\mathrm{,}8$ volt.   Ellenőrzés: $\frac{21\cdot 3\mathrm{,}5+9\cdot 4\mathrm{,}5}{30}=3\mathrm{,}8$, ami megegyezik az előzőleg kiszámított átlaggal.   $b)$ I. megoldás. Jelölje $x$ a szerdáig elfogadott jelentkezések számát. Ekkor hétfőig $x-5$, keddig $x-3$ jelentkezést fogadtak el. Jelölje $y$ a teljes buszköltséget. Ekkor megoldandó az alábbi egyenletrendszer: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{y}{x}}& {\displaystyle =\frac{y}{x-5}-\mathrm{400,}}\hfill \\ \hfill {\displaystyle \frac{y}{x}}& {\displaystyle =\frac{y}{x-3}-225.}\hfill \end{array}}$ Beszorozva a nevezőkkel: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle y\left(x-5\right)}& {\displaystyle =yx-400x\left(x-5\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle y\left(x-3\right)}& {\displaystyle =yx-225x\left(x-3\right)\mathrm{.}}\hfill \end{array}}$ Elvégezve a kijelölt műveleteket és rendezve: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 5y}& {\displaystyle =400x\left(x-5\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle 3y}& {\displaystyle =225x\left(x-3\right)\mathrm{.}}\hfill \end{array}}$ Az első egyenletből $y=80x\left(x-5\right)$, ezt a másodikba beírva: $\begin{array}{c}{\displaystyle 240x\left(x-5\right)=225x\left(x-3\right)\mathrm{.}}\end{array}$ Mivel $x\ne 0$, oszthatunk vele, és rendezés után kapjuk, hogy $x=35$. Visszahelyettesítve $y=84000$ adódik. Tehát 35 jelentkezést fogadtak el szerdáig, a teljes buszköltség pedig 84 ezer Ft volt.   Ellenőrzés: hétfőig 30 ember jelentkezett, nekik $(\frac{84000}{30}=)2800$ Ft-ot kellett volna fizetni. Keddig 32 ember jelentkezett, így egy embernek $(\frac{84000}{32}=)2625$ Ft-ot kellett volna fizetni. $2625=2800-175$ valóban. Szerdáig 35 ember jelentkezett, így egy embernek $(\frac{84000}{35}=)2400$ Ft-ot kellett fizetni. $2400=2625-225$ valóban.   II. megoldás. Jelölje $n$ a hétfőig elfogadott jelentkezések számát, és $b$ (Ft) az egy főre eső buszköltséget $n$ jelentkező esetén. Ekkor keddig $n+2$ fő jelentkezett, akiknek $b-175$ Ft-ot kellett volna fizetni, szerdáig pedig végül $n+5$ fő jelentkezett, akiknek $b-400$ Ft-ot kellett fizetni. Ekkor megoldandó az alábbi egyenletrendszer: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle nb}& {\displaystyle =\left(n+2\right)\left(b-175\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle nb}& {\displaystyle =\left(n+5\right)\left(b-400\right)\mathrm{.}}\hfill \end{array}}$ Mindkét egyenletben elvégezve a kijelölt műveleteket, és $nb$-t kivonva az egyenletek mindkét oldalából: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 0}& {\displaystyle =2b-175n-\mathrm{350,}}\hfill \\ \hfill {\displaystyle 0}& {\displaystyle =5b-400n-2000.}\hfill \end{array}}$ A második egyenletből $b=80n+400$, ezt az elsőbe beírva: $\begin{array}{c}{\displaystyle 0=2\left(80n+400\right)-175n-\mathrm{350,}}\end{array}$ ahonnan rendezés után kapjuk, hogy $n=30$. Visszahelyettesítve $b=2800$ adódik. Tehát $\left(30+5=\right)35$ jelentkezést fogadtak el szerdáig, a teljes buszköltség pedig $\left(30\cdot 2800=\right)84000$ Ft volt. Ellenőrzés mint az I. megoldásban.   3. $a)$ Oldjuk meg az alábbi egyenlőtlenséget a valós számok halmazán: $\begin{array}{c}{\displaystyle 4^x+2<9\cdot 2^{x-1}\mathrm{.}}\end{array}$ (6 pont) $b)$ Oldjuk meg az alábbi egyenletet a valós számok halmazán: $\begin{array}{c}{\displaystyle \left|\frac{3}{2}-\text{sin}x-2\text{cos}{}^{2}x\right|=\frac{1}{2}\mathrm{.}}\end{array}$ (7 pont)   Megoldás.   $a)$ Legyen $2^x=a$. Ekkor $4^x=a^2$ és $2^{x-1}=\frac{a}{2}$. Így az egyenlőtlenség a következőképpen írható fel: $a^2+2<\frac{9a}{2}$. Kettővel beszorozva és nullára rendezve: $\begin{array}{c}{\displaystyle 2a^2-9a+4<0.}\end{array}$ A $2a^2-9a+4=0$ egyenlet gyökei 4 és 0,5. Mivel a főegyüttható pozitív, az egyenlőtlenség $0\mathrm{,}5<a=2^x<4$ esetén teljesül.   Mivel a 2-es alapú exponenciális függvény szigorúan monoton nő, $2^{-1}<2^x<2^2$ pontosan akkor teljesül, ha $-1<x<2$. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{3}{2}-\text{sin}x-2\text{cos}{}^{2}x=\frac{3}{2}-\text{sin}x-2\left(1-\text{sin}{}^{2}x\right)=2\text{sin}{}^{2}x-\text{sin}x-\frac{1}{2}\mathrm{.}}& \text{(<mi>*</mi>)}\end{array}}$ Az abszolútértéket figyelembe véve két eset lehetséges: $\begin{array}{c}{\displaystyle 2\text{sin}{}^{2}x-\text{sin}x-\frac{1}{2}=\frac{1}{2}\mathrm{,}\text{vagy}2\text{sin}{}^{2}x-\text{sin}x-\frac{1}{2}=-\frac{1}{2}\mathrm{.}}\end{array}$ Nullára rendezve az egyenleteket kapjuk, hogy $\begin{array}{c}{\displaystyle 2\text{sin}{}^{2}x-\text{sin}x-1=0\text{vagy}2\text{sin}{}^{2}x-\text{sin}x=0.}\end{array}$ A $\text{sin}x$-ben másodfokú egyenleteket megoldva adódik, hogy $\text{sin}x$ értéke négyféle lehet: 1, $-\frac{1}{2}$, 0 vagy $\frac{1}{2}$. Ezekből kapjuk az egyenlet megoldásait: $\frac{\pi }{2}+2k\pi$, $\pm \frac{\pi }{6}+k\pi$ és $k\pi$ ($k\in \text{Z}$). Ekvivalens átalakításokat végeztünk.   4. $a)$ Az $\begin{array}{c}{\displaystyle f:\text{R}\to \text{R}\mathrm{,}f\left(x\right)=ax+b}\end{array}$ és a $\begin{array}{c}{\displaystyle g:\text{R}\to \text{R}\mathrm{,}g\left(x\right)={\left(x-c\right)}^2+d}\end{array}$ függvények grafikonjai az $M_1\left(-1;10\right)$ és az $M_2\left(4;-5\right)$ pontokban metszik egymást. Határozzuk meg az $a$, $b$, $c$ és $d$ értékét.  (7 pont) $b)$ Határozzuk meg az $\begin{array}{c}{\displaystyle f:\text{R}\to \text{R}\mathrm{,}f\left(x\right)=3x+7}\end{array}$ és a $\begin{array}{c}{\displaystyle g:\text{R}\to \text{R}\mathrm{,}g\left(x\right)={\left(x+3\right)}^2-6}\end{array}$ függvények által közrezárt síkidom területét.  (6 pont)   Megoldás. $a)$ $M_1$ és $M_2$ illeszkednek $f$ grafikonjára, ezért $10=-a+b$ és $-5=4a+b$. Az első egyenletből kivonva a másodikat $15=-5a$ adódik, innen pedig $a=-3$. Visszahelyettesítéssel kapjuk, hogy $b=7$. $M_1$ és $M_2$ illeszkednek $g$ grafikonjára is, ezért $10={\left(-1-c\right)}^2+d$ és $-5={\left(4-c\right)}^2+d$. Az első egyenletből kivonva a másodikat a $15={\left(-1-c\right)}^2-{\left(4-c\right)}^2$ egyenlet adódik. A négyzetre emeléseket elvégezve a másodfokú tag kiesik, és kapjuk, hogy $15=10c-15$, innen pedig $c=3$. Ezt visszahelyettesítve például az első egyenletbe $10={\left(-1-3\right)}^2+d$, ahonnan $d=-6$. Összefoglalva tehát $a=-3$, $b=7$, $c=3$ és $d=-6$, így $f\left(x\right)=-3x+7$ és $g\left(x\right)={\left(x-3\right)}^2-6$.   $b)$ Meghatározzuk a két függvény metszéspontjait. $\begin{array}{c}{\displaystyle 3x+7={\left(x+3\right)}^2-6}\end{array}$ A négyzetre emelést elvégezve és nullára rendezve: $0=x^2+3x-4$. Ennek az egyenletnek a gyökei $x_1=1$ és $x_2=-4$. Mivel a két függvény grafikonja közül az $f$ grafikonja helyezkedik el a $g$ grafikonja fölött, ezért a keresett területet a $\underset{-4}{\overset{1}{\int }}\left(f\left(x\right)-g\left(x\right)\right)\text{d}x$ integrál adja meg: ${\displaystyle \begin{array}{c}\hfill {\displaystyle f\left(x\right)-g\left(x\right)=\left(3x+7\right)-\left[{\left(x+3\right)}^2-6\right]=3x+7-\left(x^2+6x+3\right)=-x^2-3x+\mathrm{4,}}\hfill \\ \hfill {\displaystyle {\int }_{-4}^1\left(-x^2-3x+4\right)\text{d}x={\left[-\frac{x^3}{3}-\frac{3x^2}{2}+4x\right]}_{-4}^1=}\hfill \\ \hfill {\displaystyle =\left(-\frac{1}{3}-\frac{3}{2}+4\right)-\left(\frac{64}{3}-24-16\right)=\frac{13}{6}-\left(-\frac{56}{3}\right)=\frac{125}{6}\mathrm{.}}\hfill \end{array}}$ A síkidom területe tehát $\frac{125}{6}$ területegység.   II. rész     5. Egy felmérésben azt vizsgálták, az autósok hogyan viszonyulnak a téli gumiabroncsok használatához. A felmérésben $1800$ autóst kérdeztek meg. Azok, akik használnak téli gumiabroncsokat, $1320$-szal többen voltak, mint akik nem. Azok között, akik nem használnak téli gumiabroncsot, $40\%$-kal kevesebben voltak azok, akik ezt nem is tartják fontosnak, mint azok, akik ugyan fontosnak tartják, de anyagi okokból lemondanak róla. $a)$ Ábrázoljuk a felmérés eredményét kördiagramon.  (6 pont) Egyes személyautókban az autó által megtett távolságot az autó műszerei úgy számítják ki, hogy a gumiabroncs ismert kerületét és a kerék által megtett fordulatok számát összeszorozzák.   Vera észrevette, hogy néhány év használat után az autó műszerei már pontatlanul mutatták a megtett távolságot: amíg az út melletti kilométerkövek tanúsága szerint pontosan 100 km-t tett meg, addig a műszerfal 101,2 km megtett utat jelzett. Ennek az volt az oka, hogy az autó gumiabroncsai a néhány év használat alatt kicsit elkoptak, így a kerületük csökkent. A katalógusok szerint a Vera autóján használt gumiabroncsok gyártáskori átmérője 632 mm volt. A műszerek ‐ a kopást figyelmen kívül hagyva ‐ mindvégig ebből az adatból határozták meg az autó által megtett távolságot.   $b)$ Hány millimétert kopott eddig Vera autója gumiabroncsának felülete?   (5 pont) A rendőrség közúti ellenőrzés-sorozaton vizsgálja az autók gumiabroncsát. Egy nyári gumiabroncs úgynevezett profilmélysége gyártáskor kb. 8 mm. Az érvényes jogszabályok szerint nem lehet közlekedni olyan gumiabronccsal, melynek a kopása olyan mértékű, hogy profilmélysége 1,6 mm alá csökken. Felmérések alapján feltételezhető, hogy minden tizenötödik autón a gumiabroncsok kopása ezt az értéket meghaladja. (Ezt úgy tekinthetjük, hogy minden egyes autó esetén $1/15$ annak a valószínűsége, hogy a kopás 1,6 mm alá csökkent.)   $c)$ Egy járőrpáros egy napi szolgálat alatt $80$ autó gumiabroncsainak kopását ellenőrzi. Határozzuk meg annak valószínűségét, hogy legalább $5$ olyan autót találnak az ellenőrzés során, melynél a gumiabroncsok kopása meghaladja a jogszabályban előírt határértéket.  (5 pont)   Megoldás. $a)$ $\frac{1800-1320}{2}=240$ autós nem használ téli gumiabroncsot, $1800-240=1560$ autós igen. Legyen $n$ 240 téli gumiabroncsot nem használó autós közül azoknak a száma, akik anyagi okból mondanak le a használatáról, ekkor azok száma, akik nem is tartják fontosnak a használatát, $0\mathrm{,}6n$. $0\mathrm{,}6n=240-n$, ahonnan $n=150$. Tehát 150-en anyagi okokból mondanak le a téli gumiabroncs használatáról, 90-en pedig nem tartják fontosnak a használatát. A kördiagramon $1^{\circ }$  $\frac{1800}{360}=5$ autósnak felel meg.     A téli gumiabroncsot használókhoz tartozó középponti szög tehát $\frac{1560}{5}=312$ fokos, a használatról anyagi okokból lemondókhoz tartozó középponti szög $\frac{150}{5}=30$ fokos, a használatot fontosnak nem tartókhoz tartozó középponti szög pedig $\frac{90}{5}=18$ fokos.   $b)$ I. megoldás. A gumiabroncs gyártáskori kerülete $K=d\pi \approx 1985\mathrm{,}5$ mm. Ekkor 100 km megtétele alatt a kerék $\frac{100000000}{1985\mathrm{,}5}\approx 50365$-öt fordul. A kopott gumiabronccsal futó autó műszerei 101,2 km út megtételét $\begin{array}{c}{\displaystyle \frac{101200000}{1985\mathrm{,}5}\approx 50970}\end{array}$ fordulat érzékelése után jelzik. Ekkor azonban az autó ténylegesen még csak 100 km-t tett meg, tehát az abroncs kerülete $\frac{100000000}{50970}\approx 1961\mathrm{,}9$ mm, sugara $\frac{1961\mathrm{,}9}{2\pi }\approx 312\mathrm{,}2$ mm. Mivel az abroncs gyártáskori sugara 316 mm volt, ezért a felületi kopás kb. 3,8 mm volt.   II. megoldás. A műszerek a ténylegesen megtett út 1,012-szeresét érzékelték, tehát a kerék 1,012-szer annyi fordulatot tett meg, mint amennyit újkori állapotában 100 km-en fordult volna. Azaz kerülete 1,012-ed részére csökkent. Mivel a kerület és a sugár egyenesen arányos, ezért a kerék sugara is 1,012-ed részére csökkent, tehát a gumi kopott állapotában $316:1\mathrm{,}012\approx 312\mathrm{,}3$ mm-es. A felületi kopás így kb. 3,7 mm (az I. megoldásban a kerekítések miatt jött ki 3,8 mm). $c)$ ${\displaystyle \begin{array}{cc}\hfill {\displaystyle P\left(\text{legalább }5\right)}& {\displaystyle =1-P\left(\text{legfeljebb 4}\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =1-\left[P\left(0\right)+P\left(1\right)+P\left(2\right)+P\left(3\right)+P\left(4\right)\right]\mathrm{.}}\hfill \end{array}}$ Az $n=80$ és $p=\frac{1}{15}$ paraméterű binomiális eloszlás segítségével: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle P\left(0\right)}& {\displaystyle ={\left(\frac{14}{15}\right)}^{80}\approx 0\mathrm{,}\mathrm{0040,}}\hfill \\ \hfill {\displaystyle P\left(1\right)}& {\displaystyle =\left(\genfrac{}{}{0ex}{}{80}{1}\right){\left(\frac{14}{15}\right)}^{79}\cdot \frac{1}{15}\approx 0\mathrm{,}\mathrm{0229,}}\hfill \\ \hfill {\displaystyle P\left(2\right)}& {\displaystyle =\left(\genfrac{}{}{0ex}{}{80}{2}\right){\left(\frac{14}{15}\right)}^{78}\cdot {\left(\frac{1}{15}\right)}^2\approx 0\mathrm{,}\mathrm{0646,}}\hfill \\ \hfill {\displaystyle P\left(3\right)}& {\displaystyle =\left(\genfrac{}{}{0ex}{}{80}{3}\right){\left(\frac{14}{15}\right)}^{77}\cdot {\left(\frac{1}{15}\right)}^3\approx 0\mathrm{,}\mathrm{1200,}}\hfill \\ \hfill {\displaystyle P\left(4\right)}& {\displaystyle =\left(\genfrac{}{}{0ex}{}{80}{4}\right){\left(\frac{14}{15}\right)}^{76}\cdot {\left(\frac{1}{15}\right)}^4\approx 0\mathrm{,}1650.}\hfill \end{array}}$ Így $P\left(\text{legalább }5\right)=1-\left[P\left(0\right)+P\left(1\right)+P\left(2\right)+P\left(3\right)+P\left(4\right)\right]\approx 1-0\mathrm{,}3765=0\mathrm{,}6235$.   6. A valós számokon értelmezett $f\left(x\right)=2x^3+3x^2+bx+c$ függvénynek lokális maximuma van $x=-2$-nél. $a)$ Igazoljuk, hogy ekkor $b=-12$.  (5 pont) $b)$ Határozzuk meg $c$ lehetséges értékeit, ha tudjuk, hogy az $f$-nek három különböző zérushelye van.  (7 pont) $c)$ Határozzuk meg az $f$ zérushelyeit abban az esetben, ha $c=0$.  (4 pont)   Megoldás. $a)$ A függvénynek ott lehet lokális maximuma, ahol az első deriváltja nulla. $f\text{'}\left(x\right)=6x^2+6x+b$, $f\text{'}\left(-2\right)=12+b=0$, azaz valóban csak $b=-12$ lehetséges. Ellenőrizni kell még, hogy valóban lokális maximumhely-e ekkor a $-2$. $f\text{'}\text{'}\left(x\right)=12x+6$, $f\text{'}\text{'}\left(-2\right)=-18$, mivel a második derivált itt negatív, ezért a $-2$ valóban lokális maximumhely.   $b)$ A harmadfokú függvény alakját figyelembe véve akkor lesz az $f$-nek három különböző zérushelye, ha a lokális maximuma pozitív, lokális minimuma negatív értéket vesz fel. $\begin{array}{c}{\displaystyle f\text{'}\left(x\right)=6x^2+6x-12.}\end{array}$ A deriváltfüggvény zérushelyei a $-2$ és az 1, melyek közül a $-2$ lokális maximumhely, az 1 pedig lokális minimumhely. ${\displaystyle \begin{array}{cccc}\hfill {\displaystyle f\left(-2\right)}& {\displaystyle =2\cdot {\left(-2\right)}^3+3\cdot {\left(-2\right)}^2-12\cdot \left(-2\right)+c=20+c>\mathrm{0,}}\hfill & {\displaystyle \text{ahonnan}c}\hfill & \hfill {\displaystyle >-\mathrm{20,}}\\ \hfill {\displaystyle f\left(1\right)}& {\displaystyle =2\cdot 1^3+3\cdot 1^2-12\cdot 1+c=-7+c<\mathrm{0,}}\hfill & {\displaystyle \text{ahonnan}c}\hfill & \hfill {\displaystyle <7.}\end{array}}$ Összevetve: $-20<c<7$ esetén lesz $f$-nek három különböző zérushelye.   $c)$ $c=0$ esetén: $f\left(x\right)=2x^3+3x^2-12x=x\left(2x^2+3x-12\right)$. Ennek a függvénynek egyik zérushelye $x_1=0$, másik két zérushelyét a $2x^2+3x-12=0$ egyenlet megoldásai adják. Ezek (a másodfokú egyenlet megoldóképletéből) $x_{\mathrm{2,3}}=\frac{-3\pm \sqrt[]{105}}{4}$ (azaz három tizedesjegy pontossággal $-3\mathrm{,}312$ és 1,812).   7. A kanaszta nevű kártyajátékot két csomag francia kártyával játsszák. Egy csomag francia kártyában $55$ lap található: négy szín (pikk, káró, kőr, treff) mindegyikében $13$-$13$ lap (2, 3, 4, 5, 6, 7, 8, 9, 10, Bubi, Dáma, Király, Ász) van. Ezeken a lapokon kívül mindegyik csomagban van három Joker is. A pikk és treff színű lapok feketék, a káró és kőr színű lapok pirosak. A játék elején az egyik játékos kettéválasztja a jól megkevert kártyacsomagot, és a csomag egyik felében az alsó három lapot megnézheti: ez az úgynevezett emelés. Ha a három lap között van ,,szerencsés'' lap, akkor ezeket a szerencsés lapokat a játékos megkapja. Szerencsés lapnak számít a hat darab Joker, a nyolc darab 2-es (amit a kanasztában szintén Jokernek használnak) és a négy darab piros 3-as.   $a)$ Határozzuk meg annak a valószínűségét, hogy az emelést végző játékos nulla, egy, kettő, illetve három szerencsés lapot kap.  (5 pont) $b)$ Határozzuk meg annak a valószínűségét, hogy a kezdő játékosnak kiosztott első négy lap között mind a négy szín előfordul.  (4 pont) Egy szerencsejátékban $4$ Király és $4$ Ász közül visszatevés nélkül húz lapokat a játékos, egészen addig, amíg az első Ászt kihúzza. Ha az első Ász kihúzása előtt $k$ darab Királyt húzott ki, akkor a játékos nyereménye $100k^2$ forint.   $c)$ Határozzuk meg ebben a játékban a nyeremény várható értékét.  (7 pont)   Megoldás. $a)$ A kérdezett valószínűségeket hipergeometrikus eloszlás segítségével határozhatjuk meg. Összesen van a két csomagban 110 lap, ezek között 18 szerencsés, és 3 lapot húzunk ki visszatevés nélkül. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle P\left(0\right)}& {\displaystyle =\frac{\left(\genfrac{}{}{0ex}{}{92}{3}\right)}{\left(\genfrac{}{}{0ex}{}{110}{3}\right)}=\frac{125580}{215820}=\frac{2093}{3597}\approx 0\mathrm{,}\mathrm{582,}}\hfill \\ \hfill {\displaystyle P\left(1\right)}& {\displaystyle =\frac{\left(\genfrac{}{}{0ex}{}{18}{1}\right)\left(\genfrac{}{}{0ex}{}{92}{2}\right)}{\left(\genfrac{}{}{0ex}{}{110}{3}\right)}=\frac{75348}{215820}=\frac{2093}{5995}\approx 0\mathrm{,}\mathrm{349,}}\hfill \\ \hfill {\displaystyle P\left(2\right)}& {\displaystyle =\frac{\left(\genfrac{}{}{0ex}{}{18}{2}\right)\left(\genfrac{}{}{0ex}{}{92}{1}\right)}{\left(\genfrac{}{}{0ex}{}{110}{3}\right)}=\frac{14076}{215820}=\frac{391}{5995}\approx 0\mathrm{,}\mathrm{065,}}\hfill \\ \hfill {\displaystyle P\left(3\right)}& {\displaystyle =\frac{\left(\genfrac{}{}{0ex}{}{18}{3}\right)}{\left(\genfrac{}{}{0ex}{}{110}{3}\right)}=\frac{816}{215820}=\frac{68}{17985}\approx 0\mathrm{,}0038.}\hfill \end{array}}$ $b)$ Annak a valószínűsége, hogy például az első négy lap sorban pikk, káró, kőr és treff: $\begin{array}{c}{\displaystyle \frac{26}{110}\cdot \frac{26}{109}\cdot \frac{26}{108}\cdot \frac{26}{107}\approx 0\mathrm{,}0033.}\end{array}$ A négy különböző szín azonban $4!=24$-féle sorrendben kerülhet elő, ez 24 különböző (diszjunkt) lehetőség, tehát a kérdezett valószínűség az előző érték 24-szerese, azaz 0,079.   $c)$ Annak a valószínűsége, hogy 0, 1, 2, 3, illetve 4 Királyt húz a játékos az első Ász előtt: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle P\left(0\right)}& {\displaystyle =\frac{4}{8}=\frac{1}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle P\left(1\right)}& {\displaystyle =\frac{4}{8}\cdot \frac{4}{7}=\frac{2}{7}\mathrm{,}}\hfill \\ \hfill {\displaystyle P\left(2\right)}& {\displaystyle =\frac{4}{8}\cdot \frac{3}{7}\cdot \frac{4}{6}=\frac{1}{7}\mathrm{,}}\hfill \\ \hfill {\displaystyle P\left(3\right)}& {\displaystyle =\frac{4}{8}\cdot \frac{3}{7}\cdot \frac{2}{6}\cdot \frac{4}{5}=\frac{2}{35}\mathrm{,}}\hfill \\ \hfill {\displaystyle P\left(4\right)}& {\displaystyle =\frac{4}{8}\cdot \frac{3}{7}\cdot \frac{2}{6}\cdot \frac{1}{5}=\frac{1}{70}\mathrm{.}}\hfill \end{array}}$ A kérdezett várható érték így $\begin{array}{c}{\displaystyle \sum _{i=0}^{4}P\left(i\right)\cdot 100i^2=\left(\frac{1}{2}\cdot 0+\right)\frac{2}{7}\cdot 100+\frac{1}{7}\cdot 400+\frac{2}{35}\cdot 900+\frac{1}{70}\cdot 1600=160\text{ Ft.}}\end{array}$   8. Az $ABC$ egyenlőszárú háromszög alapja $AB$, beírt körének középpontja $O_1$, a beírt kör sugara 9 cm. A háromszögben olyan kört írunk, mely érinti a beírt kört és a háromszög két szárát. Ennek a körnek a középpontja $O_2$, sugara pedig 4 cm. $a)$ Határozzuk meg az egyik száron keletkező, a két kör érintési pontjai által meghatározott szakasz hosszát.  (5 pont) $b)$ Igazoljuk, hogy $O_{2}C=10\mathrm{,}4\text{cm}$.  (4 pont) $c)$ Határozzuk meg a háromszög területét.  (7 pont) Megoldás. $a)$ Jelölje az $AC$ száron a beírt kör érintési pontját $E_1$, a második kör érintési pontját pedig $E_2$. Bocsássunk merőlegest $O_2$-ből $O_1{E}_1$-re, a merőleges talppontját jelölje $T$. A derékszögű $O_1{O}_{2}T$ háromszögben $O_1{O}_2=9+4=13$ cm, $O_{1}T=9-4=5$ cm. Így a Pitagorasz-tétellel $O_{2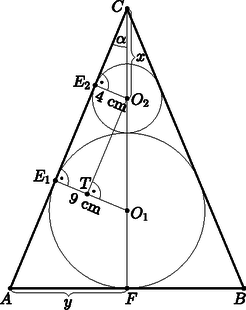}T=\sqrt[]{{13}^2-5^2}=12$ cm.     Mivel $T{O}_2{E}_2{E}_1$ téglalap, ezért $E_1{E}_2=O_{2}T=12$ cm.   $b)$ Az $O_{1}C{E}_1$ és az $O_{2}CE{}_2$ háromszögek hasonlóak, mivel megfelelő oldalaik párhuzamosak. Az $O_{2}C$ szakasz hosszát jelölje $x$. Ekkor a két háromszög megfelelő oldalainak aránya: $\frac{13+x}{9}=\frac{x}{4}$, ahonnan $x=10\mathrm{,}4$, az $O_{2}C$ szakasz hossza tehát valóban 10,4 cm.   $c)$ I. megoldás. Az $AB$ szakasz felezőpontját jelölje $F$. $CF=9+9+4+10\mathrm{,}4=32\mathrm{,}4$ cm. Az $AFC$ és az $O_2{E}_{2}C$ háromszögek hasonlóak, mert egyik hegyesszögük közös, és mindkettőnek van egy derékszöge, így szögeik megegyeznek. Az $AF$ szakasz hosszát jelölje $y$. Ekkor a két háromszög megfelelő oldalainak aránya: $\frac{AF}{CF}=\frac{E_2{O}_2}{C{E}_2}$. A Pitagorasz-tételből $C{E}_2=\sqrt[]{10\mathrm{,}{4}^2-4^2}=9\mathrm{,}6$ cm. $\frac{y}{32\mathrm{,}4}=\frac{4}{9\mathrm{,}6}$, ahonnan $y=13\mathrm{,}5$, az $AF$ szakasz hossza tehát 13,5 cm. A háromszög területe tehát $\begin{array}{c}{\displaystyle T=\frac{AB\cdot CF}{2}=\frac{2AF\cdot CF}{2}=\frac{27\cdot 32\mathrm{,}4}{2}=437\mathrm{,}4{\text{cm}}^2\mathrm{.}}\end{array}$   II. megoldás. Jelölje a háromszög szárai által bezárt szöget $2\alpha$. Ekkor $\text{sin}\alpha =\frac{4}{10\mathrm{,}4}=\frac{5}{13}\left(\approx 0\mathrm{,}385\right)$. Mivel $\alpha$ hegyesszög, azért $\begin{array}{c}{\displaystyle \text{tg}\alpha =\frac{\text{sin}\alpha }{\text{cos}\alpha }=\frac{\text{sin}\alpha }{\sqrt[]{1-\text{sin}{}^2\alpha }}=\frac{\frac{5}{13}}{\sqrt[]{1-\frac{25}{169}}}\frac{\frac{5}{13}}{\frac{12}{13}}=\frac{5}{12}}\end{array}$ (így $2\alpha \approx 45\mathrm{,}{24}^{\circ }$). Így $AF=CF\cdot \text{tg}\alpha =32\mathrm{,}4\cdot \frac{5}{12}=13\mathrm{,}5$ cm. A Pitagorasz-tételből $\begin{array}{c}{\displaystyle AC=\sqrt[]{13\mathrm{,}{5}^2+32\mathrm{,}{4}^2}=35\mathrm{,}1\text{cm.}}\end{array}$ A háromszög félkerülete: $\begin{array}{c}{\displaystyle s=\frac{27+2\cdot 35\mathrm{,}1}{2}=48\mathrm{,}6\text{cm}\mathrm{,}}\end{array}$ területe $T=\varrho s=9\cdot 48\mathrm{,}6=437\mathrm{,}4{\text{cm}}^2$.   9. Egy nyolcpontú összefüggő, egyszerű gráf csúcsai $A$, $B$, $C$, $D$, $E$, $F$, $G$ és $H$. Az $A$, $B$, $C$ és $D$ csúcsok fokszámai (ebben a sorrendben) egy növekvő számtani sorozat egymást követő tagjai. Ehhez hasonlóan az $E$, $F$, $G$ és $H$ csúcsok fokszámai (ebben a sorrendben) egy másik növekvő számtani sorozat egymást követő tagjai. A nyolc csúcs fokszámai között két egyenlő van, a többi fokszám mind különböző, továbbá $A$ fokszáma kisebb $E$ fokszámánál. $a)$ Rajzoljuk fel ezt a gráfot.  (6 pont) Egy szabályos nyolcszög két szomszédos csúcsa a derékszögű koordináta-rendszerben $A\left(0;0\right)$ és $B\left(10;0\right)$. A nyolcszög az I. és a II. síknegyedben helyezkedik el. $b)$ Írjuk fel a szabályos nyolcszög beírható körének egyenletét.  (4 pont) $c)$ Igazoljuk, hogy a $P\left(17;17\right)$ pont a nyolcszögnek belső, beírható körének viszont külső pontja.  (6 pont)   Megoldás. $a)$ Mivel a gráf összefüggő és egyszerű, a csúcsok fokszámai 1, 2, 3, 4, 5, 6 és 7 lehetnek. E számokból a következő növekvő számtani sorozatokat lehet összeállítani: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cccc}\hfill {\displaystyle \text{ 1,}}\hfill & \hfill {\displaystyle \text{3,}}\hfill & \hfill {\displaystyle \text{5,}}\hfill & \hfill {\displaystyle \text{7;}}\hfill \\ \hfill {\displaystyle \text{1,}}\hfill & \hfill {\displaystyle \text{2,}}\hfill & \hfill {\displaystyle \text{3,}}\hfill & \hfill {\displaystyle \text{4;}}\hfill \\ \hfill {\displaystyle \text{2,}}\hfill & \hfill {\displaystyle \text{3,}}\hfill & \hfill {\displaystyle \text{4,}}\hfill & \hfill {\displaystyle \text{5;}}\hfill \\ \hfill {\displaystyle \text{3,}}\hfill & \hfill {\displaystyle \text{4,}}\hfill & \hfill {\displaystyle \text{5,}}\hfill & \hfill {\displaystyle \text{6;}}\hfill \\ \hfill {\displaystyle \text{4,}}\hfill & \hfill {\displaystyle \text{5,}}\hfill & \hfill {\displaystyle \text{6,}}\hfill & \hfill {\displaystyle \text{7. }}\hfill \end{array}}}\end{array}$ Az öt sorozat között csak kettő olyan van, amelyeknek csak egy közös elemük van, ezért a gráf fokszámsorozata ($A$-tól $H$-ig) 1, 2, 3, 4, 4, 5, 6, 7. Ha $H$ fokszáma 7, akkor ez a csúcs az összes többivel össze van kötve. Mivel $A$ fokszáma 1, ezért $A$-ból $H$-n kívül más csúcsba nem vezet él. 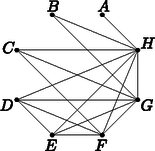    $G$ fokszáma 6, ezért $G$ az $A$-n kívül az összes többi csúccsal össze van kötve. Mivel $B$ fokszáma 2, ezért $B$-ből a $G$-n és $H$-n kívül más csúcsba nem vezet él. $F$ fokszáma 5, ezért $F$ az $A$-n és $B$-n kívül az összes többi csúccsal össze van kötve. Mivel $C$ fokszáma 3, ezért $C$-ből az $F$-en, $G$-n és $H$-n kívül más csúcsba nem vezet él. Végül $D$ és $E$ fokszáma 4, ezért ezek egymással, valamint az $F$, $G$ és $H$ csúcsokkal vannak összekötve.   $b)$ A szabályos nyolcszög egy belső szöge 135 fokos, így külső szögei 45 fokosak. Ezért $BC$ oldala egy $+1$ meredekségű egyenes egy szakasza. A 10 egység hosszú $BC$ oldal egy olyan egyenlő szárú, derékszögű háromszög átfogója, melynek befogói így $5\sqrt[]{2}$ egység hosszúak. Ezért $C\left(10+5\sqrt[]{2};5\sqrt[]{2}\right)$. A nyolcszög további oldalai is vagy párhuzamosak valamelyik koordináta-tengellyel, vagy pedig egy $+1$ vagy $-1$ meredekségű egyenesen helyezkednek el. Így a további csúcsok koordinátái: $D\left(10+5\sqrt[]{2};10+5\sqrt[]{2}\right)$, $E\left(10;10+10\sqrt[]{2}\right)$, $F\left(0;10+10\sqrt[]{2}\right)$, $G\left(-5\sqrt[]{2};10+5\sqrt[]{2}\right)$ és $H\left(-5\sqrt[]{2};5\sqrt[]{2}\right)$. A nyolcszögbe írható kör középpontja az $AE$ szakasz felezőpontja: $K\left(5;5+5\sqrt[]{2}\right)$. A kör sugara megegyezik a $K$ pont második koordinátájával: $r=5+5\sqrt[]{2}$. A kör egyenlete: $\begin{array}{c}{\displaystyle {\left(x-5\right)}^2+(y-\left(5+5\sqrt[]{2}\right){)}^2={\left(5+5\sqrt[]{2}\right)}^2\left(=75+50\sqrt[]{2}\right)\mathrm{.}}\end{array}$ $c)$ ${\displaystyle \begin{array}{cc}\hfill {\displaystyle P{K}^2}& {\displaystyle ={\left(17-5\right)}^2+(17-\left(5+5\sqrt[]{2}\right){)}^2={12}^2+{\left(12-5\sqrt[]{2}\right)}^2=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =338-120\sqrt[]{2}\mathrm{.}}\hfill \end{array}}$ Megmutatjuk, hogy ez nagyobb, mint a kör sugarának a négyzete, és ekkor $P$ valóban külső pontja a körnek: $\begin{array}{c}{\displaystyle 338-120\sqrt[]{2}>75+50\sqrt[]{2}\mathrm{,}263>170\sqrt[]{2}\mathrm{,}\text{azaz}\frac{263}{170}>\sqrt[]{2}\mathrm{.}}\end{array}$ Ez utóbbi egyenlőtlenség igaz, mert a bal oldal nagyobb, a jobb oldal pedig kisebb 1,5-nél.   Másrészt $17<10+5\sqrt[]{2}$ ekvivalens $1\mathrm{,}4<\sqrt[]{2}$-vel, ami (például a négyzetre emeléssel kapott $1\mathrm{,}96<2$ miatt) szintén igaz. Ezért $P$ első koordinátája kisebb a $C$ és $D$ csúcsok első koordinátájánál (de nagyobb a többi csúcs első koordinátájánál), valamint kisebb a $D$ és $G$ csúcsok második koordinátájánál (de nagyobb a $C$ és $H$ csúcsok második koordinátájánál), ezért $P$ a $CDGH$ téglalapnak, így a nyolcszögnek is belső pontja.