Kezdőlap


Cím:	Térbe kilépő bizonyítások IV.
Szerző(k):	Kós Géza
Füzet:	2020/január, 2 - 10. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kúpok és hasonlósági pontok

Ebben a cikksorozatban olyan bizonyításokat mutatunk be, amikor a geometriai alakzatokat ,,térbe kilépve'', három- vagy akár még magasabb dimenziós objektumok vetületeként vagy metszeteként állítjuk elő.
Ebben a részben körök hasonlósági pontjainak viselkedését fogjuk vizsgálni. Legyen

k_{1}

és

k_{2}

két kör a síkon. Mint jól tudjuk, a két kör külső hasonlósági pontja az a

H_{k}

pont, ahonnan alkalmas, pozitív arányú középpontos nagyítással a két kör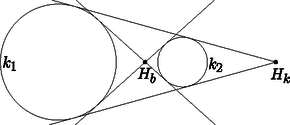

átvihető egymásba. A külső hasonlósági pont csak akkor létezik, ha a körök sugara különböző. A két kör belső hasonlósági pontja pedig az a

H_{b}

pont, ahonnan a körök negatív arányú középpontos nagyítással vihetők át egymásba. Ha a köröknek léteznek a külső közös, illetve a belső közös érintői, akkor ezek átmennek a hasonlósági pontokon (1. ábra).

1. ábra

A hasonlósági pontok szerkesztése kúpokkal

Most foglalkozzunk egy kicsit a külső hasonlósági ponttal. Legyen

k_{1}

és

k_{2}

két különböző sugarú kör, amelyeknek léteznek külső közös érintő egyenesei, a középpontjaik legyenek

O_{1}

és

O_{2}

. Az egyik közös érintő érintési pontjai legyenek

T_{1}

, illetve

T_{2}

, a másik érintő egyenes érintési pontjai

U_{1}

, illetve

U_{2}

; a két érintő metszéspontja legyen

H

. A térben illesszünk a körökre egy-egy körkúpot, amelyek alkotói ugyanakkora,

φ

szöget zárnak be a körök

Σ

síkjával. A kúpok csúcsai legyenek az

A_{1}

és

A_{2}

pontok (2. ábra).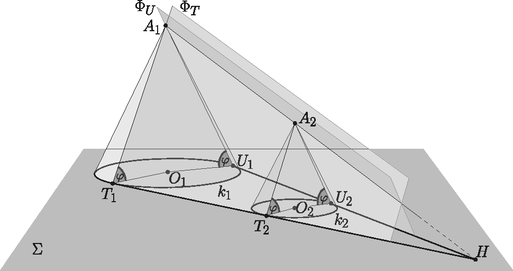

2. ábra

H

pontból nem csak a két kört, hanem a két kúpot is egymásba nagyíthatjuk, ezért az

A_{1} A_{2}

egyenes átmegy a

H

ponton. Ezt a tényt most hasonlóság nélkül is igazoljuk. A kúpok

A_{1} T_{1}

, illetve

A_{2} T_{2}

alkotóit megkaphatjuk úgy, hogy a körök

T_{1} O_{1}

, illetve

T_{2} O_{2}

sugarát

φ

szöggel elforgatjuk a

T_{1} T_{2} H

érintő körül. Ezért ezek az alkotók és a

H

pont egy

Φ_{T}

síkban vannak. Hasonlóan látjuk, hogy az

A_{1} U_{1}

és

A_{2} U_{2}

alkotók is egy

Φ_{U}

síkban vannak a

H

ponttal. A

Φ_{T}

és

Φ_{U}

síkoknak

A_{1}

A_{2}

és

H

is közös pontja, ezért ez a három pont egy egyenesen van.

Monge tétele (a három hasonlósági pont tétele)

Monge¹ tétele: Ha adott a síkon három különböző sugarú kör, egymás külsejében, és vesszük páronként a külső közös érintőik metszéspontjait, akkor ez a három pont egy egyenesre esik.

Világos, hogy itt a külső hasonlósági pontokról van szó, ezért mondjuk ki ebben az általánosabb formában:

Monge tétele, általánosabb változat: A síkon bármely három különböző sugarú kör páronként vett külső hasonlósági pontjai egy egyenesre esnek.

A tételt az előbb látott kúpokkal bizonyítjuk. Legyen a három kör

k_{1}

k_{2}

és

k_{3}

Σ

síkban, és minden

i, j

indexpárra jelölje

k_{i}

és

k_{j}

külső hasonlósági pontját

H_{i j}

. Válasszunk egy

φ

hegyesszöget, és illesszünk egy-egy kúpot a körökre, amelyeknek alkotói

φ

szöget zárnak be

Σ

-val. A kúpok csúcsai legyek

A_{1}

A_{2}

, illetve

A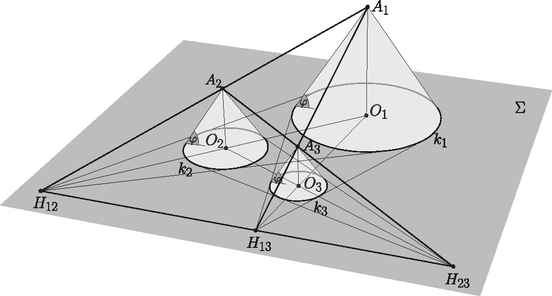_{3}

(3. ábra).

3. ábra

Bármely

i

j

indexek esetén az

A_{i} A_{j}

egyenes átmegy a

H_{i j}

ponton. Ezért mindegyik

H_{i j}

hasonlósági pont az

A_{1} A_{2} A_{3}

síkban van. Ezzel már két különböző síkot is ismerünk, amely tartalmazza a

H_{12}

H_{13}

és

H_{23}

pontot, tehát ezek egy egyenesen, a

Σ

és az

A_{1} A_{2} A_{3}

sík metszésvonalán vannak.

Mi legyen a belső hasonlósági pontokkal?

A belső hasonlósági pontokat is nehézség nélkül megszerkeszthetjük kúpokkal, csak most a kúpokat a sík ellentétes oldalára kell építenünk. Ha három körvonalra illesztünk kúpokat, és ezek közül kettő a sík egyik, a harmadik a sík másik oldalán van, akkor a Monge-tételnek egy olyan változatát kapjuk, amikor az egyik körpárnak a külső, a másik két párnak a belső hasonlósági pontját vesszük (4. ábra).

4. ábra

A Monge-tételnek ezeket a különböző változatait egységesen kezelhetjük, ha a körvonalaknak és érintő egyeneseknek irányítást adunk, vagyis nyilacskákat rajzolunk rájuk. Egy irányított körvonalnak csak az olyan irányított érintőit vesszük figyelembe, amelyeknél a kitüntetett irány megegyezik. Két irányított körvonal hasonlósági pontja azonos irányítású körök esetén az eddigi külső, ellentétes irányítású körök esetén a belső hasonlósági pont. A ,,pozitív'' irányítású körökre a sík egyik oldalán, a ,,negatív'' irányítású körökre a sík másik oldalán illesztünk kúpokat.

A Ceva- és a Menelaosz-tétel

Tanulságos lerajzolni egy ábrán három körnek mind a hat belső és külső hasonlósági pontját. Az 5. ábrán a három kör középpontja

A

B

és

C

, a belső hasonlósági pontok

A_{1}

B_{1}

és

C_{1}

, a külső hasonlósági pontok pedig

A_{2}

B_{2}

és

C_{2}

. A Monge-tétel szerint egy egyenesre esnek az

A_{2}

B_{2}

C_{2}

pontok, továbbá az

A_{2}

B_{1}

C_{1}

pontok, az

A_{1}

B_{2}

C_{1}

pontok, és az

A_{1}

B_{1}

C_{2}

pontok is. Az

A B C

és az

A_{1} B_{1} C_{1}

háromszögek megfelelő oldalainak metszéspontjai,

A_{2}

B_{2}

és

C_{2}

egyenesre esnek, ezért a Desargues-tétel szerint a megfelelő csúcsokat összekötő

A A_{1}

B B_{1}

és

C C_{1}

egyenesek egy ponton mennek át.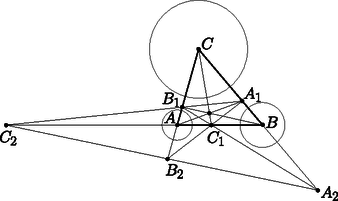

5. ábra

Ha a körök sugarai

r_{a}

r_{b}

és

r_{c}

, akkor a körök között a hasonlóságok előjeles arányai

\begin{matrix} \frac{r_{a}}{r_{b}} = - \frac{C_{1} A}{C_{1} B} = \frac{C_{2} A}{C_{2} B}, \frac{r_{b}}{r_{c}} = - \frac{A_{1} B}{A_{1} C} = \frac{A_{2} B}{A_{2} C} és \frac{r_{c}}{r_{a}} = - \frac{B_{1} C}{B_{1} A} = \frac{B_{2} C}{B_{2} A}; \end{matrix}

a szorzatuk

1

. Ezek az arányok két híres tételben is szerepelnek:

Ceva² tétele: Legyenek az

A B C

háromszög

B C

C A

, illetve

A B

oldalegyenesein

A_{1}

B_{1}

C_{1}

a csúcsoktól különböző pontok. Az

A A_{1}

B B_{1}

és

C C_{1}

egyenesek akkor és csak akkor mennek át egy ponton vagy párhuzamosak, ha

\begin{matrix} \frac{A C_{1}}{C_{1} B} \cdot \frac{B A_{1}}{A_{1} C} \cdot \frac{C B_{1}}{B_{1} A} = 1. \end{matrix}

Az állításban szereplő arányok előjelesek: az arány pozitív, ha a két szakasz ugyanabba az irányba mutat, és negatív, ha ellentétes irányúak. Az is megengedett, hogy

A_{1}

B_{1}

C_{1}

az egyenesek végtelen távoli pontjai legyenek, ilyenkor a megfelelő arány

- 1

Menelaosz³ tétele: Legyenek az

A B C

háromszög

B C

C A

, illetve

A B

oldalegyenesein

A_{2}

B_{2}

C_{2}

a csúcsoktól különböző pontok. Az

A_{2}

B_{2}

és

C_{2}

pontok akkor és csak akkor esnek egy egyenesre, ha

\begin{matrix} \frac{A C_{2}}{C_{2} B} \cdot \frac{B A_{2}}{A_{2} C} \cdot \frac{C B_{2}}{B_{2} A} = - 1. \end{matrix}

A Ceva-tételhez hasonlóan az arányok most is előjelesek, és

A_{2}

B_{2}

C_{2}

az egyenesek végtelen távoli pontjai is lehetnek.

Láthatjuk, hogy a Monge- és a Menelaosz-tétel egyik iránya lényegében ugyanaz, illetve hogy a Ceva- és a Menelaosz-tétel között az összekötő kapocs a Desargues-tétel.

,,Hasonlósági pontok'' nemeuklideszi geometriákban

A gömbi és a hiperbolikus geometriákban nincs hasonlóság. Vicces módon azonban a körök hasonlósági pontjainak szerkesztése elmondható ilyenkor is.
Ha adott két kör a hiperbolikus síkban, vannak külső közös érintőik, és ezek el is metszik egymást, akkor a metszéspontot nevezhetjük a két kör ,,hasonlósági pontjának''. A két körre egy-egy kúpot illesztve, a kúpok csúcsait összekötő egyenes átmegy a hasonlósági ponton. Ha három körünk van, bármelyik kettőnek vannak külső közös érintői, és ezek metszik egymást, akkor a Monge-tétel bizonyítását változtatás nélkül elmondhatjuk. Tehát a Monge-tétel (az eredeti, speciális formájában) igaz hiperbolikus geometriában is.
Ha bármely két kör ,,hasonlósági pontját'' szeretnénk definiálni, közös érintők felhasználása nélkül, akkor megtehetjük, hogy a két körre kúpokat illesztünk, és a síkot átdöfjük a kúpok csúcsait összekötő egyenessel. (Ha a csúcsokat összekötő egyenes nem döfi a síkot, akkor nincs hasonlósági pont.) Azt viszont mindenképpen meg kell indokolunk, hogy a szerkesztésünk különböző meredekségű kúpok esetén is mindig ugyanazt a döféspontot produkálja. Ez igazából síkbeli feladat; a kúpok tengelyein keresztül fektethetünk egy síkot, és csak ezzel a síkkal vett metszetet vizsgáljuk (6. ábra).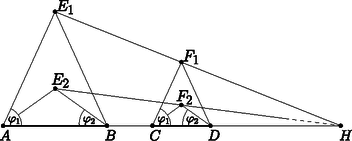

6. ábra

Vegyünk tehát két tetszőleges kört,

k_{1}

-et és

k_{2}

-t a

Σ

síkban; ezekhez szeretnénk igazolni, hogy a hasonlósági pont nem függ a

Σ

és a kúpok alkotói közötti

φ

szögtől. Vegyünk fel egy harmadik kört,

k_{3}

-at, amely kisebb, mint az első kettő, úgy, hogy a három kör középpontja ne essen egy egyenesre,

k_{3}

-nak a

k_{1}

-gyel és

k_{2}

-vel is legyenek külső közös érintői és ezek el is metsszék egymást a

H_{13}

, illetve a

H_{23}

pontban.
Most illesszünk tetszőlegesen egy-egy kúpot a

k_{1}

és

k_{2}

körökre, amelyek alkotói ugyanakkora

φ

szöget zárnak be a

Σ

síkkal; ezek csúcsai legyenek

A_{1}

, illetve

A_{2}

. Illesszünk egy harmadik kúpot a

k_{3}

körre ugyanazzal a

φ

szöggel, ennek csúcsa legyen

A_{3}

(7. ábra). (Megjegyzés: hiperbolikus geometriában nem lehet bármilyen körre bármilyen

φ

szöggel kúpot szerkeszteni, mert az alkotók nem feltétlenül metszik el a kúp tengelyét; de az igaz, hogy ha a

k_{1}

és

k_{2}

körökhöz létrejön a megfelelő kúp, akkor a náluk kisebb

k_{3}

-hoz is.)

7. ábra

Már láttuk, hogy az

A_{1} A_{3}

egyenes átmegy a

H_{13}

ponton, és az

A_{2} A_{3}

egyenes átmegy

H_{23}

-n. Az

A_{1} A_{2}

egyenes benne van a kúpok tengelyére fektetett

O_{1} A_{1} O_{2} A_{2}

síkban és a

H_{13} H_{23} A_{3}

síkban is. Ezeknek a metszésvonala a

Σ

síkkal az

O_{1} O_{2}

, illetve a

H_{13} H_{23}

egyenes, egyik sem függ a

φ

szög nagyságától.
Ha az

O_{1} O_{2}

és

H_{13} H_{23}

egyenesek metszik egymást egy

H_{12}

pontban, akkor

H_{12}

a három síknak közös pontja, tehát rajta van a harmadik metszésvonalon, az

A_{1} A_{2}

egyenesen is. Ilyenkor tehát a döféspont mindig létrejön és ugyanaz. Ha pedig az

O_{1} O_{2}

és

H_{13} H_{23}

egyenesek párhuzamosak (nem metszik egymást), akkor a három síknak nincs közös pontja, és így

A_{1} A_{2}

metszésvonalnak nem lehet pontja a

Σ

síkban.
Tehát, a

φ

nagyságától függetlenül, az

A_{1} A_{2}

egyenes vagy mindig döfi a

Σ

síkot, és mindig ugyanabban a

H_{12}

pontban, vagy pedig semmilyen

φ

esetén sem döfi, és ilyenkor nem jön létre a ,,hasonlósági'' pont.

Gömbön: hasonlósági átmérő

A gömbfelületen két körvonal közös érintői főkörök, amelyek a gömb két egymással átellenes pontjában metszik egymást. Ezért hasonlósági pontok helyett ,,hasonlósági átmérőkről'' fogunk beszélni.
Először vizsgáljuk azt az esetet, amikor a körök sugara különböző, és a közös érintők léteznek. Legyen

k_{1}

és

k_{2}

két, főkörnél kisebb körvonal az

O

középpontú

B

gömbfelületen, amelyekhez létezik két főkör, amely érinti mindkét kört úgy, hogy

k_{1}

és

k_{2}

a főköröknek ugyanazon az oldalain van. A két érintő főkör metszéspontjait jelölje

H_{1}

és

H_{2}

, az érintési pontokat az egyik közös érintőn

T_{1}

, illetve

T_{2}

, a másik érintő főkörön

U_{1}

és

U_{2}

. A két körvonalra illesszünk egy-egy ,,békaszemet'', azaz olyan

G_{1}

, illetve

G_{2}

gömböt, amely merőlegesen metszi

B

-t, és legyen

H

a két békaszem külső hasonlósági pontja (8. ábra).

8. ábra

Vegyük észre, hogy a szemgolyókat érinti a

H_{1} T_{1} T_{2} H_{2}

főkör és a gömb

O T_{1}

, illetve

O T_{2}

sugara is, ezért a szemgolyókat az

H_{1} T_{1} T_{2} H_{2}

sík is érinti, és a két szemgolyó a síknak ugyanazon az oldalán van. Ezért a

H

hasonlósági pont ebben a síkban van; sőt, a két érintési pontot összekötő

T_{1} T_{2}

egyenes átmegy a

H

ponton. Ugyanígy láthatjuk, hogy a

H_{1} U_{1} U_{2} H_{2}

sík, és benne az

U_{1} U_{2}

egyenes is átmegy

H

-n.
A

H_{1} T_{1} T_{2} H_{2}

és a

H_{1} U_{1} U_{2} H_{2}

síknak

O

H_{1}

H_{2}

és

H

is közös pontja, tehát ez a négy pont egy egyenesen van. Azt kaptuk, hogy a két körvonal ,,külső hasonlósági átmérőjének'' egyenese átmegy a körvonalakhoz tartozó békaszemek külső hasonlósági pontján.

Az általános esetben nem feltétlenül léteznek a körvonalak közös érintő főkörei. Szerencsére a békaszemek most is segítenek, és

3

-dimenziós gömbi geometria helyett elég a kúpok tengelyére illeszkedő ,,síkon'', azaz gömbfelületen belül dolgoznunk.
Legyen

c

a két kör centrálisa, vagyis az a főkör, amely átmegy a

k_{1}

és

k_{2}

középpontján; a két körrel vett metszéspontok legyenek

A

és

B

, illetve

C

és

D

. Válasszunk egy tetszőleges

φ

hegyesszöget, és a 6. ábrához hasonlóan, az

A B

és

C D

szakaszokra, a

c

-nek ugyanazon az oldalán, rajzoljunk olyan egyenlő szárú

A B E

és

C D F

gömbháromszögeket, amelyekben

E A B ∢ = A B E ∢ = F C D ∢ = C D F ∢ = φ

; ezek a háromszögek felelnek meg a két körvonalra emelt kúpoknak. A kúpokat összekötő egyenesnek az

E F

főkör felel meg; legyen az

E F

főkör és

c

két metszéspontja

H_{1}

és

H_{2}

.
Vegyük fel ismét a

G_{1}

és

G_{2}

békaszemeket, a középpontjuk legyen

O_{1}

, illetve

O_{2}

. Metsszük el a békaszemeket a

c

síkjával, és a metszetkörökre emeljünk olyan kúpokat, amelyek alkotói a

c

síkjával

φ

szöget zárnak be. A két kúp csúcsai legyenek

E'

, illetve

F'

.
Az

A E'

szakasz érinti az

A E

főkörívet, ezért

O

A

E

és

E'

egy síkban van. Hasonlóan

O

B

E

és

E'

is egy síkban van; ennek a két síknak

O

E

és

E'

közös pontjai, tehát egy egyenesen vannak. Ugyanígy látjuk, hogy

O

F

és

F'

is egy egyenesen van (9. ábra).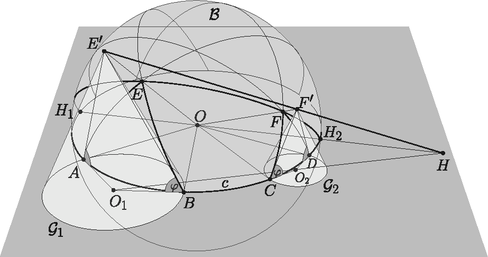

9. ábra

Tekintsük ezek után az

O_{1} O_{2}

H_{1} H_{2}

és

E' F'

egyeneseket. Mint láttuk, az

E' F'

egyenes és a

H_{1} H_{2}

egyenes is az

E F

főkör síkjában van; az

O_{1} O_{2}

és a

H_{1} H_{2}

is a

c

síkjában, végül az

O_{1} O_{2}

és az

E' F'

is a két kúp tengelyére illesztett síkban. A három egyenes tehát vagy egy ponton megy át, vagy párhuzamosak.
Ha

k_{1}

és

k_{2}

különböző sugarú, akkor a két kúp is különböző méretű, és az

E' F'

és

O_{1} O_{2}

egyenesek a két kúp, egyben a

G_{1}

és

G_{2}

békaszemek külső hasonlósági pontjában metszik egymást, tehát a

H_{1} H_{2}

egyenes is átmegy ezen a ponton.
Ha

k_{1}

és

k_{2}

sugara ugyanakkora, akkor a két kúp is ugyanakkora, tehát

E' F'

párhuzamos az

O_{1} O_{2}

egyenessel. Ebben az esetben

H_{1} H_{2}

is párhuzamos a

G_{1}

és

G_{2}

békaszemek centrálisával.
Tehát a

H_{1} H_{2}

átmérő nem függ a

φ

választásától; a hasonlósági átmérő különböző sugarú körök esetén átmegy a békaszemek külső hasonlósági pontján, egyenlő sugarú körök esetén párhuzamos a békaszemek centrálisával.

A Monge-tétel a gömbön

Most már minden készen áll ahhoz, hogy bebizonyítsuk a Monge-tétel gömbi megfelelőjét.

Monge-tétel a gömbön. A gömbfelületen bármely három (a főkörnél rövidebb) körvonal hasonlósági átmérői egy főkörön vannak.

Először vizsgáljuk azt az esetet, amikor a három körvonal sugara különböző. A gömb középpontját jelöljük

O

-val. Legyen

k_{1}

k_{2}

és

k_{3}

három tetszőleges körvonal, a hozzájuk tartozó békaszemek legyenek

G_{1}

G_{2}

, illetve

G_{3}

, a középpontjaik

O_{1}

O_{2}

, illetve

O_{3}

, a páronként vett külső hasonlósági pontjaik

H_{12}

H_{13}

és

H_{23}

(10. ábra).

10. ábra

Ha a szemeket elmetsszük az

O_{1} O_{2} O_{3}

síkkal, éppen a Monge-tétel ábráját kapjuk; a Monge-tétel szerint

H_{12}

H_{13}

és

H_{23}

egy egyenesre esik. Akkor viszont a

B

gömbnek a három hasonlósági ponton átmenő átmérői, az

O H_{12}

O H_{13}

, illetve

O H_{23}

egyenesek, mind az

O H_{12} H_{13} H_{23}

síkban, vagyis egy főkörön vannak.
Ha a három körvonal közül valamelyik kettő, például

k_{1}

és

k_{2}

ugyanakkora, akkor a hozzájuk tartozó békaszemek is ugyanakkorák, és a

H_{12}

pont nem jön létre. Ha a békaszemek sugara

r_{1} = r_{2}

és

r_{3}

, akkor

\frac{H_{13} O_{1}}{H_{13} O_{3}} = \frac{r_{2}}{r_{3}} = \frac{r_{2}}{r_{3}} = \frac{H_{23} O_{2}}{H_{23} O_{3}}

miatt a

H_{13} H_{23}

egyenes párhuzamos a

O_{1} O_{2}

egyenessel. De akkor

k_{1}

és

k_{2}

hasonlósági átmérője párhuzamos

O_{1} O_{2}

-vel és

H_{13} H_{23}

-mal, tehát az

O H_{13} H_{23}

síkban van.
Végül, ha mindhárom körvonal sugara ugyanakkora, akkor mindhárom hasonlósági átmérő párhuzamos az

O_{1} O_{2} O_{3}

síkkal, így ilyenkor is egy síkban, vagyis egy főkörön vannak.

Feladatok

1. Két pontból rajzoljunk három-három félegyenest úgy, hogy bármely két, különböző pontból induló egyenes elmetssze egymást. Ezek a félegyenesek négy négyszöget határoznak meg. Igazoljuk, hogy ha ezek közül valamelyik három érintőnégyszög, akkor a negyedik is az (11. ábra).

11. ábra

2. Bizonyítsuk be a Ceva-tételt közvetlenül, térbe kilépéssel.

3. Írjuk fel és bizonyítsuk be a Ceva- és a Menelaosz-tétel gömbi megfelelőit.

4. Az

A B C D

négyszög

A B

oldalán adott egy

P

pont. Legyen

ω

C P D

háromszög beírt köre, a középpontja

I

. Tegyük fel, hogy

ω

érinti az

A P D

és

B P C

háromszögekbe írt köröket a

K

, illetve az

L

pontban. Legyen az

A C

és

B D

egyenesek metszéspontja

E

, és legyen az

A K

és

B L

egyenesek metszéspontja

F

. Bizonyítsuk be, hogy

E

I

és

F

egy egyenesre esik. (IMO Shortlist, 2007/G8)

¹Gaspard Monge francia matematikus (1746‐1818)

²Giovanni Ceva (ejtsd: Cseva) olasz matematikus, 1647‐1734

³Alexandriai Menelaosz görög matematikus csillagász, Kr.u. kb. 70‐140