Cím:	Megoldásvázlatok a 2019/8. szám emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Sztranyák Attila (Budapest)
Füzet:	2019/december, 526 - 537. oldal	PDF  |  MathML

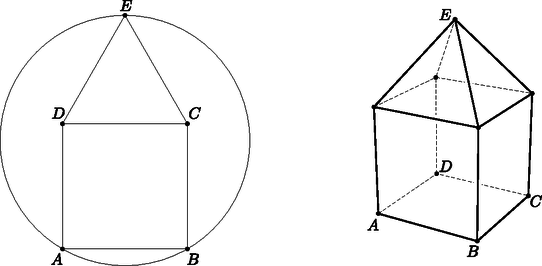
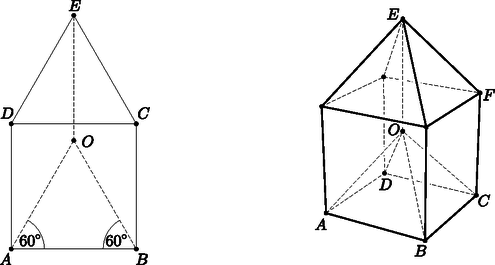
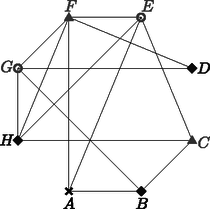
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ A bal oldali ábrán egy 1 cm oldalhosszú négyzet és rajta egy 1 cm oldalhosszú szabályos háromszög látható. Mekkora annak a körnek a sugara, amely átmegy az $A$, $B$, $E$ pontokon?  (5 pont)     $b)$ A jobb oldali ábrán egy 1 cm élhosszú kocka és rajta egy olyan 1 cm élhosszú szabályos gúla látható, amelynek minden oldallapja szabályos háromszög. Mekkora annak a gömbnek a sugara, amely átmegy az $A$, $B$, $C$, $D$, $E$ pontokon?  (7 pont)   Megoldás. $a)$ Toljuk el $DCE$ szabályos háromszögünket a $\overrightarrow{CB}$ vektorral. A háromszög képe az eltolás után az $ABO$ szabályos háromszög ($A=D\text{'}$, $B=C\text{'}$, $O=E\text{'}$) lesz; emiatt $OA=OB=1$. Másfelől mivel $O=E\text{'}$ ezért $OE=1$; azaz $O$ pont az $A$, $B$, $E$ köréírt körének a középpontja, és a kör sugara 1 cm.     $b)$ Voltaképpen ugyanazt csináljuk, mint két dimenzióban. Jelöljük a kocka $C$ ,,fölötti'' csúcsát $F$-fel, és toljuk el a térben a szabályos gúlánkat az $\overrightarrow{FC}$ vektorral. Ekkor a gúla képe az eltolás után az $ABCDO$ szabályos gúla lesz (ahol $O=E\text{'}$ az $E$ pont eltolt képe). Mivel $ABCDO$ a megfelelő szabályos gúla képe, ezért $AO=BO=CO=DO=1$, míg $O=E\text{'}$ miatt $EO=1$, azaz az $O$ pont egyenlő távolságra van $A$, $B$, $C$, $D$, $E$ pontoktól, vagyis ezen pontok köréírható gömbjének a középpontja, és a gömb sugara 1 cm.   Megjegyzés. A feladat megoldható számolással is, de mi nem ezt az utat követtük.   2. Egy $2019$ mezőből álló játéktáblánk van a következő ábra szerint:     $($Az $\mathrm{1,2,3,4,5}$ számok vannak rajta ciklikusan, összesen $2019$ hosszan.$)$ Az $1$-es mezőről indulunk, és minden mezőről annyit lépünk jobbra, amennyi az ott lévő szám. $a)$ Összesen hányra lépünk rá a mezők közül?  (4 pont) $b)$ Mennyi azon mezők számainak összege, amire nem lépünk rá?  (3 pont) $c)$ A játékszabályokat a következőképpen módosítjuk: egy szabályos hatoldalú kockával dobunk, ha a dobás eredménye az $1$ és $5$ közötti $d$ szám, akkor az első mező, amire rálépünk az első $d$; míg ha a dobás hatos, akkor az első $1$-esre lépünk, és innentől kezdve minden mezőről annyit lépünk jobbra, amennyi az ott lévő szám. Az első száz mező közül várhatóan hány mezőt látogatunk meg?  (4 pont)   Megoldás. $a)$ Megvizsgálva az első pár lépést azt kapjuk, hogy az első tizenegy mező közül rendre az $1\Rightarrow 2\Rightarrow 4\Rightarrow 3$ (ez már a második 3-as) $\Rightarrow 1$ (ez már a harmadik 1-es) lépünk. Mivel innen ciklikusan ismétlődnek a mezők, tíz egymás utáni mezőből pontosan 4-re lépünk rá. $2019=201\cdot 10+9$, azaz lesz 201 darab teljes ciklusunk, valamint további 9 mezőnk. Az utolsó 9 mező közül 4-re lépünk rá, így összesen $201\cdot 4+4=808$ mezőre lépünk rá. $b)$ Egy teljes ciklusban a meg nem látogatott mezők összege: $3+5+1+2+4+5=20$, míg az utolsó 9 mező közül (hiányzik egy 5-ös a teljes ciklushoz) a meg nem látogatottak összege csak 15. Azaz azon mezők összege, amire nem lépünk rá: $201\cdot 20+15=4035$. $c)$ A módosított szabályok szerint $\frac{2}{6}=\frac{1}{3}$ eséllyel az első $1$-es mezőröl indulok, míg az első 2-es, $\text{...}$, 5-ös mezőről indulás esélye $\frac{1}{6}$. Az $1$-es, $2$-es, $3$-as, $4$-es mezőről indulva rendre ugyanazt az $\mathrm{1,2,4,3}$ ciklust kapjuk, csak az elején, illetve a végén különböznek. Ez alapján $\mathrm{1,2,3,4}$-gyel kezdve az első 100 mező közül rendre 40, 39, 40, 38 mezőre lépünk rá; míg az első 5-ösből indulva pontosan az 5-ösöket látogatjuk meg, így összesen 20 darab mezőt. Innen a meglátogatott mezők várható száma: $\begin{array}{c}{\displaystyle \frac{2\cdot 40+39+40+38+20}{6}=\frac{217}{6}\approx 36\mathrm{,}17.}\end{array}$   3. Piszkos Fred a kapitány hosszú tengeri útra indul hajójával. Egy $100$ literes hordóban tiszta alkoholt visz magával. Fred a hordóból minden éjfélkor megiszik $5$ liter löttyöt, majd felmegy a hídra és a hajó kormánykerekét eltekeri ${30}^{\circ }$-kal. Ezek után visszavonul a kabinjába és a következő éjfélig alszik. A matrózok minden nappal során feltöltik a hordót esővízzel, de a kormánykerékhez nem nyúlnak. Ha a hordó alkoholtartalma $50\%$ alá csökken és a kapitány iszik belőle, akkor kijózanodik. $a)$ Az indulás után hanyadik éjfélkor józanodik ki Fred?  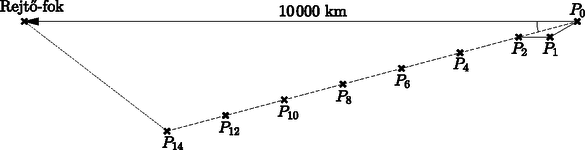(4 pont) Fred fogadott egy hordó rumba Watson kapitánnyal, hogy az ő hajója gyorsabb, mint Watson fregattja. A verseny április elsején $23$ óra $59$-kor indult. A két hajó egyszerre indult el a nyugati irányban pontosan $10000$ kilométerre lévő közös célpont, a Rejtő-fok felé. Watson hajója állandó $8$ csomó sebességgel haladt, míg Fred teknője $6$ csomóval. $(1$ csomó sebesség megegyezik $1\mathrm{,}85\frac{\text{km}}{\text{h}}$-val.$)$ Fred amíg részeg, minden páros sorszámú nap éjfélén balra tekeri ${30}^{\circ }$-kal a kormánykereket, míg a páratlan sorszámú napokon jobbra; amikor viszont kijózanodik, akkor azonnal a megfelelő irányba állítja a kormánykereket (és a helyes irányt a továbbiakban tartja is). A józan Piszkos Fred továbbá minden éjfélkor képes a hajó aktuális sebességét $10\%$-kal növelni (és ezt az egész következő nap tartani). $b)$ Melyik kapitány nyeri a fogadást?  (9 pont)   Megoldás. $a)$ A feladat szövege alapján az indulás időpontjában $a_0=1$ (azaz 100%) a hordó alkoholtartalma. Mivel minden újabb időpontban elfogy 5 liter lötty, amit 5 liter 0%-os alkoholtartalmú vízzel pótoltak, így $n$ nap múlva a hordó alkoholtartalma: $a_n=0\mathrm{,}{95}^n$. A kapitány akkor józanodik ki, ha $a_n<0\mathrm{,}5$ lesz. A megfelelő egyenletet megoldva: $0\mathrm{,}{95}^n=0\mathrm{,}5\Rightarrow n=\frac{\text{ln}0\mathrm{,}5}{\text{ln}0\mathrm{,}95}\approx 13\mathrm{,}51$; mivel a $0\mathrm{,}{95}^x$ függvény szigorúan monoton csökken ez azt jelenti, hogy $a_{13}>0\mathrm{,}5$, de $a_{14}<0\mathrm{,}5$, azaz Fred pontosan az indulás után két héttel józanodik ki. $b)$ Először számoljuk ki, hogy az egyenletes sebességgel pontosan a cél irányába mozgó Watson mennyi idő alatt éri el a Rejtő-fokot. $\begin{array}{c}{\displaystyle v_w=8\cdot 1\mathrm{,}85\frac{\text{km}}{\text{h}}=14\mathrm{,}8\frac{\text{km}}{\text{h}}\Rightarrow t_w=\frac{10000\text{km}}{14\mathrm{,}8\frac{\text{km}}{\text{h}}}\approx 675\mathrm{,}68\text{h}\approx 28\text{ nap és }3\mathrm{,}68\text{h}}\end{array}$ alatt ér célba. Most lássuk mit csinált eközben Fred. Fred sebessége kezdetben $\begin{array}{c}{\displaystyle v_F=6\cdot 1\mathrm{,}85\frac{\text{km}}{\text{h}}=11\mathrm{,}1\frac{\text{km}}{\text{h}}\Rightarrow s=11\mathrm{,}1\cdot 24=266\mathrm{,}4\text{ km-t}}\end{array}$ tesz meg 1 nap alatt Piszkos Fred. Használjuk a következő ábra jelöléseit.     Jelölje $P_0\mathrm{,}{P}_1\mathrm{,}{P}_2\mathrm{,}\text{...}\mathrm{,}{P}_{14}$ Fred hajójának a pozícióját rendre a startnál, illetve $\mathrm{1,2,}\text{...}$ és 14 nap múlva. Mivel a párosadik napokon balra, a páratlanadik napokon jobbra fordítja el a kormányt Fred, ezért minden második nap pontosan nyugat felé halad a hajó, illetve két ilyen napot ,,összevonva'' egy olyan rombusz két szomszédos oldalán halad végig Fred teknője, amelynek oldalai 266,4 km hosszúak és az általuk bezárt szög ${150}^{\circ }$. Innen két másodszomszédos éjféli időpont pozíciója között (pl. $P_0$ és $P_2$, vagy $P_{12}$ és $P_{14}$ között) a távolság számítható koszinusz-tétellel: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle P_0{P}_2^2}& {\displaystyle =266\mathrm{,}{4}^2+266\mathrm{,}{4}^2-2\cdot 266\mathrm{,}4\cdot 266\mathrm{,}4\cdot \text{cos}{150}^{\circ }\approx 264859\mathrm{,}8\Rightarrow }\hfill \\ \hfill {\displaystyle \Rightarrow P_0{P}_2}& {\displaystyle \approx 514\mathrm{,}645\text{km}\mathrm{.}}\hfill \end{array}}$ Azaz két hét alatt Fred a starttól $514\mathrm{,}645\cdot 7=3602\mathrm{,}515$ km-re került és pontosan ${15}^{\circ }$-kal tért el a nyugati iránytól. Számítsuk ki egy újabb koszinusz tétellel, mennyi út van még hátra (a pontos irányt hagyjuk meg a Kapitánynak). A hátralévő útra: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle s_F^2}& {\displaystyle =10{000}^2+3602\mathrm{,}{515}^2-2\cdot 10000\cdot 3602\mathrm{,}515\cdot \text{cos}{15}^{\circ }\approx 43382869\Rightarrow }\hfill \\ \hfill {\displaystyle \Rightarrow s_F}& {\displaystyle \approx 6586\mathrm{,}567\text{km}}\hfill \end{array}}$ út van még hátra két hét után. Lássuk, mennyi idő alatt teszi meg a józan Fred ezt az utat. Jelöljük $b_n$-nel a két hét utáni $n$-edik napon Fred hajója által megtett utat (kilométerben). Ekkor $b_n=266\mathrm{,}4\cdot 1\mathrm{,}{1}^{n-1}$. Az első $n$ nap során ekkor $\begin{array}{c}{\displaystyle s_n=b_1+b_2+\text{...}+b_n=266\mathrm{,}4\cdot \frac{1\mathrm{,}{1}^n-1}{1\mathrm{,}1-1}=2664\left(1\mathrm{,}{1}^n-1\right)=2664\cdot 1\mathrm{,}{1}^n-2664\text{km-t}}\end{array}$ tesz meg. Azt keressük, hogy mikor lesz $s_n=6586\mathrm{,}567$. ${\displaystyle \begin{array}{c}\hfill {\displaystyle s_n=2664\cdot 1\mathrm{,}{1}^n-2664=6586\mathrm{,}567\Rightarrow 2664\cdot 1\mathrm{,}{1}^n=9250\mathrm{,}567\Rightarrow }\hfill \\ \hfill {\displaystyle \Rightarrow 1\mathrm{,}{1}^n=\frac{9250\mathrm{,}567}{2664}\Rightarrow n=\frac{\text{ln}(\frac{9250\mathrm{,}567}{2664})}{\text{ln}1\mathrm{,}1}\approx 13\mathrm{,}061.}\hfill \end{array}}$ Mivel az $1\mathrm{,}{1}^x$ függvény szigorúan monoton növő, ezért ez azt jelenti, hogy (kijózanodása után) 13 nap alatt még nem ér célba Fred, de a 14-dik, vagyis összességében a 28-dik napon már eléri a Rejtő-fokot. Azaz Piszkos Fred nyeri a fogadást (és így a hordó rumot), hiszen körülbelül egy nappal korábban ér a célba, mint Watson.   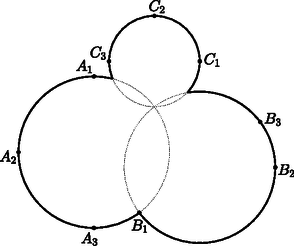4. Az ábra egy park térképét ábrázolja. A parkot három körvonal határolja; a körök rendre az $A_1\left(-2;3\right)$, $A_2\left(-7;-2\right)$, $A_3\left(-2;-7\right)$, illetve a $B_1\left(1;-6\right)$, $B_2\left(10;-3\right)$, $B_3\left(9;0\right)$, valamint a $C_1\left(5;4\right)$, $C_2\left(2;7\right)$, $C_3\left(-1;4\right)$ pontok által meghatározott körök köréírt körei. $a)$ Igazoljuk, hogy az $A_1{A}_2{A}_3$, a $B_1{B}_2{B}_3$, valamint a $C_1{C}_2{C}_3$ háromszögek mind derékszögű háromszögek.   (4 pont)     $b)$ Igazoljuk, hogy az $A_3$, $B_1$, $B_2$, valamint a $B_3$, $C_1$, $C_2$, illetve a $C_3$, $A_1$, $A_2$ ponthármasok rendre egy-egy egyenesre esnek.  (3 pont) $c)$ A park építésze egy ,,különleges'' helyre kutat szeretne fúratni. Úgy tűnik neki, hogy a parkot alkotó három kör egy közös pontban metszi egymást (ami eléggé különleges lenne). Igaza van-e az építésznek? Ha igen, pontosan hol van ez a pont?   (8 pont)   Megoldás. $a)$ Az ábra alapján úgy tűnik, hogy a háromszögek olyan háromszögek, ahol a 2-es indexű csúcs szöge derékszög, míg a másik két csúcsot összekötő átfogó egyben a kör átmérője is. Ezt fogjuk igazolni. Az $A_1$, $A_3$ pontok távolsága 10, az $O_A$ felezőpontjuk koordinátái: $O_A\left(-2;-2\right)$. Ez a felezőpont pedig pontosan 5 távolságra van $A_2$-től, azaz ez a háromszög egyenlőszárú és derékszögű háromszög, és a köréírt kör sugara 5. Hasonlóan a $C_1$, $C_3$ pontok távolsága 6, az $O_C$ felezőpontjuk koordinátái: $O_C\left(2;4\right)$. Ez a felezőpont pedig pontosan 3 távolságra van $C_2$-től, azaz ez a háromszög is egyenlőszárú és derékszögű háromszög, és a köréírt kör sugara 3. Míg a $B_1$, $B_3$ pontok távolsága Pitagorasz tételével: $\sqrt[]{8^2+6^2}=10$, az $O_B$ felezőpontjuk koordinátái: $O_B\left(5;-3\right)$. Ez a felezőpont pedig pontosan 5 távolságra van $B_2$-től, azaz ez a háromszög is derékszögű háromszög (de nem egyenlőszárú), és a köréírt kör sugara 5. $b)$ Azt fogjuk használni, hogy ha a $P$, $Q$, $R$ pontokra igaz az, hogy $\overrightarrow{PQ}=c\cdot \overrightarrow{PR}$ valamely $c$ valós számra, akkor a három pont egy egyenesre esik. Az $A_3$, $B_1$, $B_2$ pontokra: $\overrightarrow{A_3{B}_1}=\left(3;1\right)$, míg $\overrightarrow{A_3{B}_2}=\left(12;4\right)=4\cdot \overrightarrow{A_3{B}_1}$, azaz $A_3$, $B_1$, $B_2$ valóban egy egyenesre esnek. A $B_3$, $C_1$, $C_2$ pontokra: $\overrightarrow{B_3{C}_1}=\left(-4;4\right)$, míg $\overrightarrow{B_3{C}_2}=\left(-7;7\right)=\frac{7}{4}\cdot \overrightarrow{B_3{C}_1}$, azaz a $B_3$, $C_1$, $C_2$ pontok is egy egyenesre esnek. A $C_3$, $A_1$, $A_2$ pontokra: $\overrightarrow{C_3{A}_1}=\left(-1;-1\right)$, míg $\overrightarrow{C_3{A}_2}=\left(-6;-6\right)=6\cdot \overrightarrow{C_3{A}_1}$, azaz a $C_3$, $A_1$, $A_2$ pontok is egy egyenesre esnek. $c)$ Az $a)$ pont alapján a körök egyenletei rendre: $k_A:{\left(x+2\right)}^2+{\left(y+2\right)}^2=25$; $k_B:{\left(x-5\right)}^2+{\left(y+3\right)}^2=25$; $k_C:{\left(x-2\right)}^2+{\left(y-4\right)}^2=9$. Számítsuk ki $k_A$ és $k_B$ metszéspontjait. Ezekre a metszéspontokra igaz: ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\left(x+2\right)}^2+{\left(y+2\right)}^2={\left(x-5\right)}^2+{\left(y+3\right)}^2\Rightarrow }\hfill \\ \hfill {\displaystyle \Rightarrow x^2+4x+4+y^2+4y+4=x^2-10x+25+y^2+6y+9\Rightarrow }\hfill \\ \hfill {\displaystyle \Rightarrow 14x-26=2y\Rightarrow y=7x-13.}\hfill \end{array}}$ Ezt a (hatványvonal) egyenletet visszahelyettesítve mondjuk $k_A$ egyenletébe kapjuk: ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\left(x+2\right)}^2+{\left(7x-11\right)}^2=25\Rightarrow x^2+4x+4+49x^2-154x+121-25=0\Rightarrow }\hfill \\ \hfill {\displaystyle \Rightarrow 50x^2-150x+100=0\Rightarrow x^2-3x+2=\left(x-1\right)\left(x-2\right)=0.}\hfill \end{array}}$ Innen a $k_A$ és $k_B$ körök metszéspontjai: $\left(1;-6\right)$ és $\left(2;1\right)$. Ha ezek közül bármelyik rajta van a harmadik körön, akkor készen vagyunk. Vizsgáljuk meg, hogy a $\left(2;1\right)$ pont koordinátái teljesítik-e a harmadik köregyenletet. ${\left(2-2\right)}^2+{\left(1-4\right)}^2=0^2+{\left(-3\right)}^2=9$, azaz ez a metszéspont rajta van a $k_C$ körön is (a másik metszéspont nincs rajta). Ezzel megvagyunk, a három kör valóban egy közös pontban, a $\left(2;1\right)$ pontban metszi egymást. II. rész     5. $a)$ Adjuk meg a $h\left(x\right)=\text{cos}2x-\text{sin}2x+2\text{sin}{}^{2}x+1$ függvény szélsőértékeit. Hol veszi fel a szélsőértékeit a függvény?  (6 pont) $b)$ Legyen $f\left(x\right)=x^2-2x+2$, míg a $g_n\left(x\right)$ a következőképpen definiált függvény-sorozat: $\begin{array}{c}{\displaystyle g_1\left(x\right)=f\left(x\right);g_n\left(x\right)=f\left(g_{n-1}\left(x\right)\right)\left(\text{ha }n\ge 2\right)\mathrm{.}}\end{array}$ Adjuk meg $g_{2019}(\frac{3}{2})$ tizedesvessző utáni első $100$ számjegyét.  (10 pont)   Megoldás. $a)$ A duplaszögek addíciós képleteivel: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle h\left(x\right)}& {\displaystyle =\text{cos}2x-\text{sin}2x+2\text{sin}{}^{2}x+1=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\text{cos}{}^{2}x-\text{sin}{}^{2}x-2\text{sin}x\text{cos}x+2\text{sin}{}^{2}x+1=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\text{cos}{}^{2}x-2\text{sin}x\text{cos}x+\text{sin}{}^{2}x+1={\left(\text{cos}x-\text{sin}x\right)}^2+1.}\hfill \end{array}}$ Mivel ${\left(\text{cos}x-\text{sin}x\right)}^2\ge 0$, ezért $h\left(x\right)\ge 1$ és ezt az 1 minimumértéket $h\left(x\right)$ fel is veszi mindenütt, ahol $\text{cos}x=\text{sin}x\Rightarrow \text{tg}x=1$, azaz a minimum helyei: $x=\frac{\pi }{4}+k\cdot \pi$ $\left(k\in \text{Z}\right)$. Maximum ott lehet, ahol a $j\left(x\right)=\text{cos}x-\text{sin}x$ különbségnek pozitív maximuma, vagy negatív minimuma van. Deriváljuk a $j\left(x\right)$ függvényt: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle j\text{'}\left(x\right)}& {\displaystyle =-\text{sin}x-\text{cos}x\mathrm{,}}\hfill \\ \hfill {\displaystyle j\text{'}\left(x\right)}& {\displaystyle =0\iff \text{sin}x=-\text{cos}x\iff \text{tg}x=-1\iff x=\frac{3\pi }{4}+k\cdot \pi \left(k\in \text{Z}\right)\mathrm{.}}\hfill \end{array}}$ ,,Minden'' esetben $j\text{'}\text{'}\left(x\right)=-\text{cos}x+\text{sin}x\ne 0$, azaz ezek valódi szélsőértékei $j\left(x\right)$-nek, és mivel ezeken a helyeken $|j\left(x\right)|=2\cdot \frac{\sqrt[]{2}}{2}=\sqrt[]{2}$, ezért minden ilyen helyre ${\left(\text{cos}x-\text{sin}x\right)}^2+1=j^2\left(x\right)+1={\left(\sqrt[]{2}\right)}^2+1=3$. Azaz $h\left(x\right)$ maximuma 3 és a maximumának helyei: $x=\frac{3\pi }{4}+k\cdot \pi$ $\left(k\in \text{Z}\right)$. $b)$ Írjuk fel $f\left(x\right)$-t $f\left(x\right)=x^2-2x+2={\left(x-1\right)}^2+1$ alakban, és vizsgáljuk meg a $g_1\left(x\right)\mathrm{,}{g}_2\left(x\right)\mathrm{,}{g}_3\left(x\right)\mathrm{,}\text{...}$ függvények értékeit $x=\frac{3}{2}$-nél. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle g_1\left(\frac{3}{2}\right)}& {\displaystyle =f\left(\frac{3}{2}\right)={\left(\frac{3}{2}-1\right)}^2+1=\frac{1}{4}+1=\frac{1}{2^{2^1}}+1}\hfill \\ \hfill {\displaystyle }\\ \hfill {\displaystyle \text{(ezt ne is alakítsuk tovább);}}\\ \hfill {\displaystyle g_2\left(\frac{3}{2}\right)}& {\displaystyle =f\left(g_1\left(\frac{3}{2}\right)\right)={\left(\frac{1}{4}+1-1\right)}^2+1=\frac{1}{16}+1=\frac{1}{2^{2^2}}+1;}\hfill \\ \hfill {\displaystyle g_3\left(\frac{3}{2}\right)}& {\displaystyle =f\left(g_2\left(\frac{3}{2}\right)\right)={\left(\frac{1}{16}+1-1\right)}^2+1=\frac{1}{256}+1=\frac{1}{2^{2^3}}+1.}\hfill \end{array}}$ Mivel ${\displaystyle \begin{array}{cc}\hfill {\displaystyle f\left(\frac{1}{2^{2^n}}+1\right)}& {\displaystyle ={\left(\frac{1}{2^{2^n}}+1-1\right)}^2+1={\left(\frac{1}{2^{2^n}}\right)}^2+1=\frac{1}{{\left(2^{2^n}\right)}^2}+1=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{1}{2^{2^n\cdot 2}}+1=\frac{1}{2^{2^{n+1}}}+\mathrm{1,}}\hfill \end{array}}$ ezért adódik, hogy $g_n(\frac{3}{2})=\frac{1}{2^{2^n}}+1$, azaz $g_{2019}(\frac{3}{2})=\frac{1}{2^{2^{2019}}}+1$. Vizsgáljuk csak $\frac{1}{2^{2^{2019}}}$-t. $\begin{array}{c}{\displaystyle 0<\frac{1}{2^{2^{2019}}}<\frac{1}{2^{2019}}<\frac{1}{2^{334}}<\frac{1}{{10}^{100}}}\end{array}$ (ez utóbbi $1024=2^{10}>{10}^3=1000$ miatt igaz); azaz $\frac{1}{2^{2^{2019}}}$, és így $\frac{1}{2^{2^{2019}}}+1=g_{2019}(\frac{3}{2})$ tizedesvessző utáni első száz jegye mind 0.   6. Néhány vegyianyag-szállító kamionban különféle kóddal $\left(A\mathrm{,}B\mathrm{,}C\mathrm{,}D\mathrm{,}E\mathrm{,}F\mathrm{,}G\mathrm{,}H\right)$ ellátott palackokat szállítanak. A robbanásveszély miatt bizonyos palackokat nem szabad együtt szállítani. Ezeket a ,,tiltásokat'' a következő táblázat tartalmazza:   ${\displaystyle \begin{array}{|ccccc|}\hline {\displaystyle \text{Vegyi anyag címkéje: }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi></math>}}\hfill \\ {\displaystyle \text{Ezzel nem szállítható: }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi><mn>,</mn><mi>E</mi><mn>,</mn><mi>F</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mn>,</mn><mi>C</mi><mn>,</mn><mi>G</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi><mn>,</mn><mi>E</mi><mn>,</mn><mi>H</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>F</mi><mn>,</mn><mi>G</mi></math>}}\hfill \\ {\displaystyle \text{Vegyi anyag címkéje: }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>E</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>F</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>G</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>H</mi></math> }}\hfill \\ {\displaystyle \text{Ezzel nem szállítható: }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mn>,</mn><mi>C</mi><mn>,</mn><mi>F</mi><mn>,</mn><mi>H</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mn>,</mn><mi>D</mi><mn>,</mn><mi>E</mi><mn>,</mn><mi>G</mi><mn>,</mn><mi>H</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi><mn>,</mn><mi>D</mi><mn>,</mn><mi>F</mi><mn>,</mn><mi>H</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi><mn>,</mn><mi>E</mi><mn>,</mn><mi>F</mi><mn>,</mn><mi>G</mi></math> }}\hfill \\ \hline\end{array}}$   $a)$ Legalább hány kamion kell, ha minden anyagból pontosan egy-egy palackot kell elszállítanunk? (Minden kamionba legfeljebb négy palack fér el.)  (6 pont) $b)$ Hány kamion kell, ha minden anyagból pontosan $5$-$5$ palackot kell elszállítani? (Most is minden kamionba legfeljebb négy palack fér el.)  (6 pont) $c)$ Véletlenszerűen kiválasztva két különböző palackot mennyi az esélye annak, hogy azokat nem tehetjük egy kamionra?  (4 pont)   Megoldás. $a)$ Rajzoljuk meg a feladat gráfját (két vegyianyag-kódot akkor kötünk össze, ha a két palack nem szállítható együtt).     Színezzük ki a gráf csúcsait úgy, hogy bármely két olyan csúcs, amit él köt össze, különböző színt kapjon. Megmutatjuk, hogy bármely ilyen színezéshez legalább négy szín kell (azaz a gráf csúcs-kromatikus száma 4), ami azt jelenti, hogy legalább négy kamion kell a palackok szállításához. Indirekt tegyük fel, hogy a gráf csúcsai 3 színnel jól színezhetőek. Ekkor a teljes 3-klikket alkotó $F$, $G$, $H$ csúcsoknál ezt a három színt fel is kell használnunk. Legyen $F$, $G$, $H$ színe rendre zöld, piros és kék; (innen fonalasan) $\Rightarrow$ $E$ színe csak piros, $D$ színe csak kék, $C$ színe csak zöld, $B$ színe csak kék lehet (mert mindegyiknek van másik két színű szomszédja). Ekkor viszont $A$ csúcsnak lesz piros ($E$), kék ($B$) és zöld ($F$) színű szomszédja is, vagyis $A$ megszínezéséhez szükséges egy negyedik szín is. Ezzel igazoltuk, hogy a gráf csúcs-kromatikus száma legalább 4; 4 színnel pedig (mondjuk $A$-t sárgának választva) a csúcsok jól színezhetőek. Az eddigiek alapján a szállításhoz legalább 4 kamion kell (az azonos színekkel jelölt palackok kerülnek egy kamionba). Egy lehetséges szétosztás:   ${\displaystyle \begin{array}{|cccc|}\hline \hfill {\displaystyle \text{1. kamion }}\hfill & \hfill {\displaystyle \text{ 2. kamion }}\hfill & \hfill {\displaystyle \text{ 3. kamion }}\hfill & \hfill {\displaystyle \text{ 4. kamion }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi><mn>,</mn><mi>H</mi><mn>,</mn><mi>D</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi><mn>,</mn><mi>F</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>E</mi><mn>,</mn><mi>G</mi></math> }}\hfill \\ \hline\end{array}}$   $b)$ Mivel 40 palack van, ezért minimum 10 kamion kell. Ez viszont elég is, ahogyan a következő táblázat mutatja (nagyon sok különböző megoldás lehet).   ${\displaystyle \begin{array}{|ccccc|}\hline \hfill {\displaystyle \text{1. kamion }}\hfill & \hfill {\displaystyle \text{ 2. kamion }}\hfill & \hfill {\displaystyle \text{ 3. kamion }}\hfill & \hfill {\displaystyle \text{ 4. kamion }}\hfill & \hfill {\displaystyle \text{ 5. kamion }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mi>A</mi><mi>A</mi><mi>H</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi><mi>B</mi><mi>B</mi><mi>B</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi><mi>C</mi><mi>C</mi><mi>C</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mi>A</mi><mi>C</mi><mi>D</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi><mi>D</mi><mi>D</mi><mi>D</mi></math> }}\hfill \\ \hfill {\displaystyle \text{6. kamion }}\hfill & \hfill {\displaystyle \text{ 7. kamion }}\hfill & \hfill {\displaystyle \text{ 8. kamion }}\hfill & \hfill {\displaystyle \text{ 9. kamion }}\hfill & \hfill {\displaystyle \text{ 10. kamion }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi><mi>E</mi><mi>E</mi><mi>F</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>E</mi><mi>E</mi><mi>E</mi><mi>G</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>F</mi><mi>F</mi><mi>F</mi><mi>F</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>G</mi><mi>G</mi><mi>G</mi><mi>G</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>H</mi><mi>H</mi><mi>H</mi><mi>H</mi></math> }}\hfill \\ \hline\end{array}}$   $c)$ A feladat gráfjában 14 él van (a táblázatbeli bejegyzések száma 28, de a szimmetria miatt ez 14 párt jelent); azaz pontosan 14 pár olyan palack van, amik nem kerülhetnek össze. 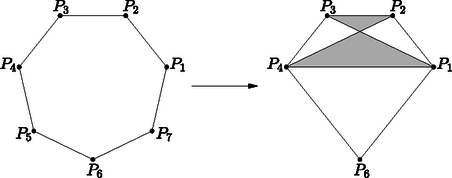Innen a kérdéses valószínűség: $\begin{array}{c}{\displaystyle P=\frac{\text{,,kedvező'' párok száma}}{\text{összes párok száma}}=\frac{14}{\left(\genfrac{}{}{0ex}{}{8}{2}\right)}=\frac{14}{28}=\frac{1}{2}\mathrm{.}}\end{array}$   7. Egy cég gyémánt alakú emblémája olyan ötszög, melynek csúcsai egy szabályos hétszög megfelelő $(P_1$, $P_2$, $P_3$, $P_4$, $P_6)$ csúcsai $($lásd jobb oldali ábra).     A cég $10000$ darab az emblémával ellátott kitűzőt rendelt. A nyomdai költségekben két tétellel kell kalkulálni: $10000$ centiméternyi vonal megrajzolása $50$ euróba kerül, míg $10000{\text{cm}}^2$-nyi terület besatírozása $200$ euróba. $a)$ Mennyi lesz a $10000$ kitűző nyomdai költsége, ha a szabályos hétszög egy-egy oldala 2 cm hosszú?  (10 pont) $b)$ A cég piárosa úgy találta, hogy az embléma nem elég színes. Szeretné a gyémánt $5$ összefüggő részében megjeleníteni a piros, a fehér és a zöld színeket. Hányféle különböző ilyen három színű emblémát kaphatunk, ha azt szeretnénk, hogy az élben szomszédos részek színe különböző legyen, valamint mind a három szín meg is jelenjen az emblémában?  (6 pont)   Megoldás. $a)$ Számítsuk ki a szabályos hétszög kétféle átlójának a hosszát. Koszinusztétellel: $\begin{array}{c}{\displaystyle P_1{P}_3^2=2^2+2^2-2\cdot 2\cdot 2\cdot \text{cos}\frac{{900}^{\circ }}{7}\approx 12\mathrm{,}988\Rightarrow P_1{P}_3\approx 3\mathrm{,}\mathrm{604,}}\end{array}$ míg $\begin{array}{c}{\displaystyle P_1{P}_4^2=2^2+P_1{P}_3^2-2\cdot 2\cdot P_1{P}_3\cdot \text{cos}\left(\frac{{900}^{\circ }}{7}\cdot \frac{4}{5}\right)\approx 20\mathrm{,}196\Rightarrow P_1{P}_4\approx 4\mathrm{,}494.}\end{array}$ Innen a vonalak megrajzolásának költsége: $\begin{array}{c}{\displaystyle \approx \left(3\cdot 2+4\cdot 3\mathrm{,}604+4\mathrm{,}494\right)\cdot 50=24\mathrm{,}91\cdot 50=1245\mathrm{,}5\text{ euró.}}\end{array}$ Kiszámoljuk a satírozott részek területeit is. A $P_1{P}_3$ és $P_2{P}_4$ metszéspontját jelöljük $O$-val. $P_2{P}_{3}O$ olyan egyenlőszárú háromszög, melynek $P_2{P}_3$ alapja 2 cm hosszú, míg alapján fekvő szögei nagysága: $\frac{{180}^{\circ }}{7}$, innen az alaphoz tartozó $m$ magasságra: $\text{tg}(\frac{{180}^{\circ }}{7})=m\approx 0\mathrm{,}4816$ és így $\begin{array}{c}{\displaystyle T_{P_2{P}_{3}O}\approx \frac{2\cdot 0\mathrm{,}4816}{2}=0\mathrm{,}4816.}\end{array}$ A $P_1{P}_{4}O$ háromszög pedig hasonló $P_2{P}_{3}O$-hoz, és a hasonlóság aránya éppen $\lambda =\frac{P_1{P}_4}{P_2{P}_3}\approx \frac{4\mathrm{,}494}{2}=2\mathrm{,}247$, innen $T_{P_1{P}_{4}O}\approx 2\mathrm{,}{247}^2\cdot 0\mathrm{,}4816\approx 2\mathrm{,}4314$. Innen a satírozás költsége: $\approx \left(0\mathrm{,}4816+2\mathrm{,}4314\right)\cdot 200=582\mathrm{,}6$ euró. Azaz a nyomdai összköltség hozzávetőlegesen: $1245\mathrm{,}5+582\mathrm{,}6=1828\mathrm{,}1$ euró. $b)$ Jelöljük lentről felfele a részeket $R_1\mathrm{,}{R}_2\mathrm{,}{R}_3\mathrm{,}{R}_4\mathrm{,}{R}_5$-tel ($R_2$ az az egyetlen rész, amelynek 3 szomszédja van, az $R_3$, $R_4$ részek az egybevágó kisebb háromszögek.) ‐ $R_2$ kitöltésére $3$ lehetőségünk van. ‐ Ha ekkor $R_3$ és $R_4$ színe különböző (ez kétféleképpen lehetséges), akkor $R_5$ színénél nincs választási lehetőségünk, ugyanazt a színt kapja $R_5$, mint $R_2$; viszont $R_1$-re két különböző színt is választhatunk. Az esetek száma itt $3\cdot 2\cdot 1\cdot 2=12$. ‐ Ha azonban $R_3$ és $R_4$ színe azonos (ez is kétféleképpen lehetséges), akkor eddig csak két színt használtunk fel, azaz vagy $R_1$, vagy $R_5$ (vagy mindkettő) színe a harmadik szín kell, hogy legyen. Ha csak $R_1$ kapja a harmadik színt, akkor $R_5$ színe egyértelmű, hasonlóan ha csak $R_5$ kapja a harmadik színt, akkor $R_1$ színe egyértelmű, és az is egyértelmű eset, ha mindkét területet a harmadik színnel színezem (ez így összesen háromféle lehetséges színezés); azaz ezen az ágon $3\cdot 2\cdot 3=18$ lehetséges eset van. Összesen tehát $12+18=30$-féleképp lehet kiszínezni az emblémát.   8. Egy speciális trópusi halaknak való felül nyitott, alul és oldalt üveg akváriumot építünk. Az akvárium paramétereire EU-előírások alapján a következőknek kell teljesülnie: ‐ Az akvárium térfogata $1{\text{m}}^3$ kell, hogy legyen;   ‐ az akvárium alapja olyan téglalap, melynél az oldalak aránya $1:2;$   ‐ a négy oldalfal olyan üvegből készül, melynek ára $90$ euró négyzetméterenként;   ‐ az akvárium alsó lapja pedig olyan üvegből készül, melynek négyzetmétere $120$ euróba kerül. Milyennek válasszuk az akvárium éleit, hogy a lehető legkevesebb legyen az anyagköltség, és az hány euró lesz?  (16 pont)   Megoldás. Jelöljük az akvárium alaplapjának oldalait $x\mathrm{,2}x$-szel (a 2. feltétel alapján), míg a magasságát $y$-nal. Ekkor a feltételek alapján $V=2x^{2}y=1\Rightarrow \Rightarrow y=\frac{1}{2x^2}$. Az anyagköltségfüggvényt $f\left(x\mathrm{,}y\right)$-nak nevezve pedig teljesül: $\begin{array}{c}{\displaystyle f\left(x\mathrm{,}y\right)=2x^2\cdot 120+2\left(2xy\right)\cdot 90+2\left(xy\right)\cdot 90=240x^2+540xy\mathrm{.}}\end{array}$ Ennek a költségfüggvénynek szeretnénk a (lokális) szélsőértékeit megtalálni. $f\left(x\mathrm{,}y\right)$-ba behelyettesítve $y=\frac{1}{2x^2}$-t a költségfüggvény már csak $x$-től függ: $f\left(x\right)=240x^2+\frac{270}{x}$. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle f\text{'}\left(x\right)}& {\displaystyle =480x-\frac{270}{x^2}\mathrm{,}}\hfill \\ \hfill {\displaystyle f\text{'}\left(x\right)}& {\displaystyle =0\iff 480x=\frac{270}{x^2}\Rightarrow x^3=\frac{270}{480}\Rightarrow x=\sqrt[3]{\frac{27}{48}}=\frac{3}{2\sqrt[3]{6}}\approx 0\mathrm{,}8255.}\hfill \end{array}}$ Vizsgáljuk meg $f\left(x\right)$ második deriváltját is: $f\text{'}\text{'}\left(x\right)=480+\frac{540}{x^2}>0$, azaz a függvénynek a kapott helyen valóban lokális minimuma van. Számoljuk ki $y$-t: $\begin{array}{c}{\displaystyle y=\frac{1}{2x^2}=\frac{1}{2\cdot \frac{9}{4\sqrt[3]{36}}}=\frac{2\sqrt[3]{36}}{9}\approx 0\mathrm{,}7338.}\end{array}$ Azt kaptuk, hogy az optimális akvárium alapélei, illetve magassága (méterben): $x\approx 0\mathrm{,}8255$; $2x\approx 1\mathrm{,}651$; $y\approx 0\mathrm{,}7338$ és ekkor a (minimális) anyagköltség: $f\left(x\mathrm{,}y\right)\approx 490\mathrm{,}6$ euró.   9. Hány olyan $0<\frac{a}{b}<1$ és $0<\frac{c}{d}<1$ $\left(a\mathrm{,}b\mathrm{,}c\mathrm{,}d\in {\text{N}}^{+}\right)$ nem egyszerűsíthető közönséges tört van, hogy az $\begin{array}{c}{\displaystyle \left(1+\frac{a}{b}\right)\left(1+\frac{c}{d}\right)}\end{array}$ szorzat egész, valamint $a+b+c+d=100?$  (16 pont)   Megoldás. Mivel $\frac{a}{b}$, $\frac{c}{d}$  0 és 1 közé esik, azért $1<(1+\frac{a}{b})(1+\frac{c}{d})<4$, azaz a szorzat csak 2, vagy 3 lehet. A két esetet külön vizsgáljuk. Ha $\begin{array}{c}{\displaystyle \left(1+\frac{a}{b}\right)\left(1+\frac{c}{d}\right)=2\Rightarrow 1+\frac{c}{d}=\frac{2b}{a+b}\Rightarrow \frac{c}{d}=\frac{2b}{a+b}-1=\frac{b-a}{a+b}\mathrm{.}}\end{array}$ Ha a törtek nem egyszerűsíthetőek, akkor $c=b-a$, és $d=a+b$ kell, hogy teljesüljön, ráadásul $a$-nak és $b$-nek különböző paritásúnak kell lennie (mert különben $c$ és $d$ is páros, és így $\frac{c}{d}$ egyszerűsíthető lenne). Mivel $a+b+c+d=100\Rightarrow a+b+b-a+a+b=a+3b=100\Rightarrow a=100-3b$. Innen ha $b$ páratlan, akkor $a=100-3b$ is páratlan; míg ha $b$ páros, akkor $a$ is páros. Ekkor viszont (bármelyik esetben) $c=b-a$ és $d=b+a$ is páros ellentmondásban azzal, hogy a $\frac{c}{d}$ tört nem egyszerűsíthető. Azaz ezen az ágon nem kapunk megoldást. Ha $\begin{array}{c}{\displaystyle \left(1+\frac{a}{b}\right)\left(1+\frac{c}{d}\right)=3\Rightarrow 1+\frac{c}{d}=\frac{3b}{a+b}\Rightarrow \frac{c}{d}=\frac{3b}{a+b}-1=\frac{2b-a}{a+b}\mathrm{.}}\end{array}$ Ha a törtek nem egyszerűsíthetőek, akkor $c=2b-a$, és $d=a+b$ kell, hogy teljesüljön. Mivel $a+b+c+d=100\Rightarrow a+b+2b-a+a+b=a+4b=100\Rightarrow b=25-\frac{a}{4}$. Innen $a$ 4-gyel osztható szám, míg $b$ nagyobb, de legfeljebb kétszer akkora (az eddigiek alapján). A lehetőségeket $a$, $b$-re (és a számolt $c$, $d$-re) soroljuk fel egy táblázatban.   ${\displaystyle \begin{array}{|cccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>b</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi><mo stretchy="false">=</mo><mn>2</mn><mi>b</mi><mo stretchy="false">-</mo><mi>a</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>d</mi><mo stretchy="false">=</mo><mi>b</mi><mo stretchy="false">+</mo><mi>a</mi></math> }}\hfill & \hfill {\displaystyle }\hfill & {\displaystyle }\hfill \\ \hfill {\displaystyle \text{4}}\hfill & \hfill {\displaystyle \text{ 24 }}\hfill & \hfill {\displaystyle \text{ 44 }}\hfill & \hfill {\displaystyle \text{ 28 }}\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{ a törtek egyszerűsíthetőek }}\hfill \\ \hfill {\displaystyle \text{8}}\hfill & \hfill {\displaystyle \text{ 23 }}\hfill & \hfill {\displaystyle \text{ 38 }}\hfill & \hfill {\displaystyle \text{ 31 }}\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi><mo stretchy="false">></mo><mi>d</mi></math> így <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi><mo stretchy="false">/</mo><mi>d</mi><mo stretchy="false">></mo><mn>1</mn></math> }}\hfill \\ \hfill {\displaystyle \text{12}}\hfill & \hfill {\displaystyle \text{ 22 }}\hfill & \hfill {\displaystyle \text{ 32 }}\hfill & \hfill {\displaystyle \text{ 34 }}\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{ a törtek egyszerűsíthetőek }}\hfill \\ \hfill {\displaystyle \text{16}}\hfill & \hfill {\displaystyle \text{ 21 }}\hfill & \hfill {\displaystyle \text{ 26 }}\hfill & \hfill {\displaystyle \text{ 37 }}\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{ ez megoldás }}\hfill \\ \hfill {\displaystyle \text{20}}\hfill & \hfill {\displaystyle \text{ 20 }}\hfill & \hfill {\displaystyle \text{ 20 }}\hfill & \hfill {\displaystyle \text{ 40 }}\hfill & \hfill {\displaystyle }\hfill & {\displaystyle \text{ a törtek egyszerűsíthetőek, illetve <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo>≥</mo><mi>b</mi></math> }}\hfill \\ \hline\end{array}}$   Vagyis azt kaptuk, hogy az egyetlen megoldás: $a=16$, $b=21$, $c=26$, $d=37$. Ezt leellenőrizve ($a\mathrm{,}b$ illetve $c\mathrm{,}d$ valóban relatív prímek) $\begin{array}{c}{\displaystyle \left(1+\frac{16}{21}\right)\left(1+\frac{26}{37}\right)=\left(\frac{37}{21}\right)\left(\frac{63}{37}\right)=\frac{63}{21}=3.}\end{array}$