Kezdőlap


Cím:	Térbe kilépő bizonyítások III.
Szerző(k):	Kós Géza
Füzet:	2019/december, 516 - 522. oldal	PDF \| MathML

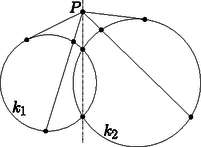
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Hatványvonalak és hatványsíkok

Ebben a cikksorozatban olyan bizonyításokat mutatunk be, amikor a geometriai alakzatokat ,,térbe kilépve'', három- vagy akár még magasabb dimenziós objektumok vetületeként vagy metszeteként állítjuk elő.

A harmadik részben körök hatványvonalaival és gömbök hatványsíkjaival fogunk játszani. Legyen a

k

egy körvonal, a középpontja

O

, sugara

r

, és

P

tetszőleges pont a síkon, az

O

-tól

d

távolságra. Húzzunk

P

-n keresztül egy

e

egyenest, ami elmetszi

k

-t az

A

és

B

pontokban; a szelőtétel szerint a

P A \cdot P B

előjeles szorzat nem függ az

e

választásától. Ezt a számot hívjuk a

P

pontnak a

k

körre vonatkozó hatványának.
Az 1. ábrán az

O

-n átmenő szelőről leolvashatjuk, hogy a hatvány értéke

P A_{0} \cdot P B_{0} = (d - r) (d + r) = d^{2} - r^{2}

. Ha

P

a körön kívül van, akkor a szelő két határhelyzete a két

P

-ből húzott érintő, ezért ha az érintő szakaszok hossza

P T_{1} = P T_{2} = t

, akkor a

O P T_{1}

és

O P T_{2}

derékszögű háromszögekből is megkaphatjuk, hogy a hatvány értéke

t^{2} = d^{2} - r^{2}

1. ábra

2. ábra

Ha nem egy, hanem két körünk van,

k_{1}

és

k_{2}

, és a középpontjuk különböző, akkor azoknak a pontoknak a halmaza a síkon, amelyeknek a két körre vonatkozó hatványa egyenlő, egy egyenes; ezt az egyenest hívjuk

k_{1}

és

k_{2}

hatványvonalának. A hatványvonal merőleges a két kör centrálisára¹.
Térben, ha

G_{1}

és

G_{2}

két gömb a térben, és a középpontjuk különböző, akkor azoknak a pontoknak a halmaza, amelyeknek a két gömbre vonatkozó hatványa egyenlő, egy sík; ezt a síkot hívjuk

G_{1}

és

G_{2}

hatványsíkjának.
Azt, hogy két kör hatványvonala egyenes, az iskolában koordinátákkal vagy vektorokkal szoktuk levezetni; felírjuk az

(x, y)

pont hatványait a két körre, és vesszük a kettő különbségét. A különbség egy kétváltozós lineáris függvény, tehát egy egyenes egyenlete.

Miért egyenes a hatványvonal?

Az iskolai levezetésből tudjuk, hogy a hatványvonal egyenes, csak az nem teljesen világos, hogy miért. Lássunk egy másik bizonyítást, amelyből közvetlenül derül ki, hogy a kérdéses pontok tényleg egy egyenesen vannak.
Vegyük fel a

k_{1}

és

k_{2}

köröket a

Σ

síkban, és nevezzünk egy

P \in Σ

pontot érdekesnek, ha a

P

-ből

k_{1}

-hez és

k_{2}

-höz húzott érintő szakaszok egyenlő hosszúak. (A definícióból sajnos kimaradnak a körökön belüli pontok; a bizonyításunk csak a kívül elhelyezkedő pontokra fog működni.) Konstruálunk egy egyenest, ami átmegy az összes érdekes ponton.
Illesszünk a két körvonalra egy-egy gömbfelületet, amelyek sugara ugyanakkora; a gömbök legyenek

G_{1}

és

G_{2}

, középpontjuk

K_{1}

, illetve

K_{2}

. A gömböket úgy válasszuk, hogy

K_{1}

és

K_{2}

Σ

síknak ugyanazon az oldalán legyenek.
Tekintsünk tetszőlegesen egy érdekes

P

pontot a

Σ

síkban, és húzzunk

P

-ből egy-egy érintőt a két körhöz; a két érintési pont legyen

T_{1}

, illetve

T_{2}

. A

P T_{1}

és

P T_{2}

egyenesek nem csak a két kört, hanem a két gömböt is érintik (3. ábra).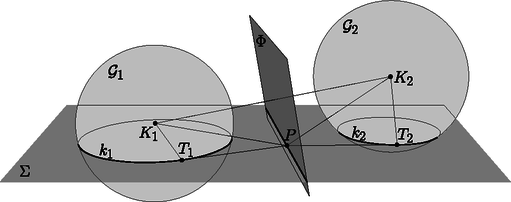

3. ábra

P K_{1} T_{1}

háromszög egybevágó a

P K_{2} T_{2}

háromszöggel, mert

K_{1} T_{1} = K_{2} T_{2}

a két gömb közös sugara,

P T_{1} = P T_{2}

az érdekes

P

pontból a körökhöz húzott érintő szakaszok, és

P T_{1} K_{1} ∢ = P T_{2} K_{2} ∢ = 90^{\circ}

, mert a gömböt érintő szakaszok merőlegesek az érintési pontból húzott sugarakra. Ezért a háromszögek átfogói is egyenlők,

P K_{1} = P K_{2}

; ez viszont azt jelenti, hogy a

P

pont a

K_{1} K_{2}

szakasz felező merőleges síkjában van.
Jelöljük a

K_{1} K_{2}

szakasz felező merőleges síkját

Φ

-vel. A

K_{1}

és

K_{2}

pont választása miatt

Σ

nem lehet azonos

Φ

-vel, például mert

Φ

felezi, míg

Σ

nem is metszi a

K_{1} K_{2}

szakaszt.
Az érdekes pontok nem csak a

Σ

-nak, hanem a

Φ

síknak is pontjai. Ez a két sík különböző, tehát a közös részük vagy üres, vagy egy egyenes. Az érdekes pontok tehát, ha egyáltalán léteznek, a két sík metszésvonalán vannak.
Érdemes meggondolni, hogy a két sík mikor lehetne párhuzamos. A

Φ

sík merőleges a

K_{1} K_{2}

szakaszra, ezért a két sík párhuzamosságának feltétele, hogy a

K_{1} K_{2}

szakasz is merőleges legyen

Σ

-ra. Ebben az esetben a két középpont,

K_{1}

és

K_{2}

vetülete

Σ

-n egybeesne, vagyis

k_{1}

és

k_{2}

koncentrikus² lenne.

Hatványvonalak nemeuklideszi geometriákban

Az előbbi bizonyítást többféle irányban is lehetséges kiterjeszteni, általánosítani. Az első, kézenfekvő irány a dimenzió növelése. Térben, két gömb hatványsíkja mindig sík, és ezt úgy igazolhatjuk, hogy a gömbfelületekre azonos sugarú, 4-dimenziós gömböket illesztünk. Ezt ugyan nem tudjuk elképzelni és lerajzolni, de minden más lépés gond nélkül működik.
Van egy másik irány, ami talán nem annyira nyilvánvaló. A bizonyításunkban csak háromszögek egybevágóságát és szimmetriát (szakaszfelező merőleges síkot) használtunk; nem volt szükségünk párhuzamosságra és hasonlóságra. Ezért a bizonyítás olyan geometriai struktúrákban is elmondható, ahol nincs párhuzamosság és hasonlóság.

A gömbi geometriában, az eddigi sík helyett, a pontok egy egységsugarú gömbfelület pontjai, az egyenesek helyét a gömb főkörei veszik át. Két pont távolsága a pontokat összekötő (rövidebb) főkörív hossza. A gömbfelületen is bármelyik két körvonalhoz definiálhatjuk az ,,érdekes'' pontokat.
Ugyanaz az okoskodás a gömbön is működik, persze a

G_{1}

és

G_{2}

gömböket egy

1

-gyel magasabb dimenziójú gömbi geometriában kell elhelyeznünk; a bizonyítás végén azok a pontok, amelyek egyenlő távol vannak a

K_{1}

és

K_{2}

pontoktól, egy

2

-dimenziós gömbfelületen vannak, és a két gömbfelület metszete egy főkör. Megint csak a személyes korlátainkkal kell megküzdenünk, amikor az elrendezést megpróbáljuk elképzelni vagy lerajzolni.

A hiperbolikus geometriák létezését egymástól függetlenül Bolyai János³ és Nyikolaj Lobacsevszkij⁴ bizonyította be, ők publikáltak először olyan geometriai rendszereket, amelyekben a szokásos euklideszi axiómák teljesülnek, kivéve a párhuzamossági axiómát, ami helyett az igaz, hogy bármely egyeneshez bármely rajta kívül fekvő pontból végtelen sok párhuzamost lehet húzni. (A nemeuklideszi geometriák kutatásában Gaussnak⁵ is voltak publikálatlan eredményei.)
A Pitagorasz- és a szelőtételnek is léteznek megfelelői a gömbi és hiperbolikus geometriákban, ezért pont körre vagy gömbre vonatkozó hatványát is lehet képletekkel definiálni. Sajnos a Pitagorasz- és a szelőtételek nemeuklideszi alakja kicsit különbözik, és különböző hatványfogalmakat tennének logikussá.
Az alábbi táblázatban összegyűjtöttem a Pitagorasz-tétel, pont körre vonatkozó hatványa és a szelőtétel gömbön és a hiperbolikus geometriákban érvényes megfelelőit. A

k

rögzített pozitív szám a hiperbolikus geometria paramétere (egyfajta skálázás),

r

a kör sugara,

d

a pontnak a középponttól való távolsága,

x_{1}

x_{2}

és

t

két egyirányú szelődarab, illetve a körhöz húzott érintő szakasz hossza. A

ch

és

th

a hiperbolikus koszinusz-, illetve tangensfüggvény:

ch x = \frac{e^{x} + e^{- x}}{2}

th x = \frac{e^{2 x} - 1}{e^{2 x} + 1}

\begin{matrix} Pitagorasz-tétel & Hatvány def. & szelőtétel (alternatív def.) \\ euklideszi & t^{2} + r^{2} = d^{2} & d^{2} - r^{2} & x_{1} \cdot x_{2} = (d + r) (d - r) \\ gömbi & cos t cos r = cos d & \frac{cos d}{cos r} & tan \frac{x_{1}}{2} \cdot tan \frac{x_{2}}{2} = tan \frac{d + r}{2} tan \frac{d - r}{2} \\ hip. & ch \frac{t}{k} ch \frac{r}{k} = ch \frac{d}{k} & \frac{ch \frac{d}{k}}{ch \frac{r}{k}} & th \frac{x_{1}}{2 k} \cdot th \frac{x_{2}}{2 k} = th \frac{d + r}{2 k} th \frac{d - r}{2 k} \end{matrix}

Ezekből a képletekből le lehet vezetni, hogy a hatványvonal egyenes, illetve főkör, de az előbb látott térbe kilépés is működik: ugyanúgy definiálhatjuk az érdekes pontokat, és elismételhetjük a bizonyítást. A hiperbolikus eset végén egyetlen furcsa közjáték történhet: a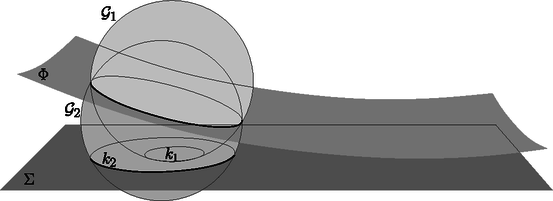

Σ

és a

Φ

síkok úgy is lehetnek párhuzamosak, hogy a

k_{1}

és

k_{2}

körök középpontja különböző; a hatványvonal ilyenkor nem jön létre (4. ábra).

4. ábra

Alternatív bizonyítás a gömbön: a békaszem-módszer

A gömbi esetben a nehézségeinket az okozta, hogy plusz egy dimenziót már felhasználtunk a gömbfelület elhelyezéséhez, és a háromdimenziós gömbi geometriát már csak a négydimenziós euklideszi térbe tudnánk beágyazni. Most mutatok egy olyan bizonyítást, amikor a kétdimenziós gömbfelületből a háromdimenziós euklideszi térbe lépünk ki, így nem lesz szükségünk még egy dimenzióra. Az euklideszi tételeink közül fel fogjuk használni, hogy két különböző középpontú gömb hatványsíkja egy síkfelület.
Legyen

B

egy

O

középpontú gömbfelület, és rajta

k_{1}

és

k_{2}

két különböző, főkörnél kisebb körvonal. Nevezzük

B

egy

P

pontját érdekesnek, ha

P

-ből a két körvonalhoz egyenlő hosszúságú érintő főköríveket lehet húzni. Azt szeretnénk igazolni, hogy az érdekes pontok a

B

gömb valamelyik főkörén vannak.
Legyen

G_{1}

és

G_{2}

az a két gömb, amely

k_{1}

, illetve

k_{2}

mentén merőlegesen metszi

B

-t. (A

B

gömb a béka teste,

G_{1}

és

G_{2}

a két szemgolyója.)
Tekintsünk egy tetszőleges érdekes

P

pontot a

B

felületen, és legyen

T_{1}

és

T_{2}

egy-egy olyan pont a két körvonalon, amelyre a

P T_{1}

és

P T_{2}

főkörívek érintik

k_{1}

-t, illetve

k_{2}

-t (5. ábra).

5. ábra

G_{1}

gömb merőlegesen metszi

B

-t, ezért

G_{1}

-et érinti a

B

gömb

O T_{1}

sugara; ezen kívül a

P T_{1}

főkör is érinti. Ezért

G_{1}

-et érinti az

O P T_{1}

sík és vele együtt a

P T_{1}

szakasz is. Hasonlóan láthatjuk, hogy a

P T_{2}

szakasz érinti a

G_{2}

gömböt. A feltevésünk szerint

P

egy érdekes pont, vagyis a

P T_{1}

és

P T_{2}

ívek egyforma hosszúak; ebből következik, hogy a

P T_{1}

és

P T_{2}

szakaszok is egyforma hosszúak. Tehát a

P

pontból egyforma hosszú érintőt lehet húzni a

G_{1}

és

G_{2}

gömbökhöz. Ezért a

P

pont benne van a

G_{1}

és

G_{2}

gömbök hatványsíkjában. Jelöljük ezt a síkot

Φ

-vel.
Vegyük észre, hogy az

O

pontból a

G_{1}

és

G_{2}

gömbökhöz húzott

O T_{1}

és

O T_{2}

érintők is egyforma hosszúak, mert a

B

sugarai. Tehát

O

is a

Φ

síkban van. Az összes érdekes pont a

B

gömbfelület és a középpontján átmenő

Φ

sík közös részében van, ami egy főkör.

Azonos meredekségű kúpok metszete

Gömbök hatványsíkjainak egy alkalmazása a következő, jól ismert tétel.

Tétel. Ha két egyenes körkúppalást tengelye párhuzamos, és a nyílásszögük ugyanakkora, akkor a két kúp közös pontjai egy síkban vannak.

(Ezt a tételt is könnyű lenne koordinátákkal bizonyítani, lásd a 3. feladatot).
Jelöljük két kúpot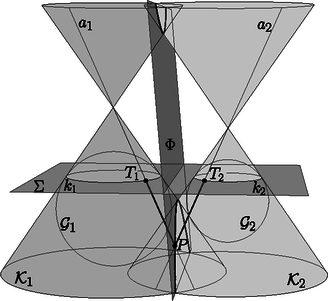

K_{1}

-gyel és

K_{2}

-vel, és metsszük el a kúpokat egy, a tengelyekre merőleges

Σ

síkkal; a két metszetkör legyen

k_{1}

és

k_{2}

. Legyen

G_{1}

és

G_{2}

az a két gömb, amely

k_{1}

, illetve

k_{2}

mentén érinti a két kúppalástot (6. ábra).

6. ábra

Tekintsük a két kúpnak egy közös

P

pontját. Ezen átmegy a kúpoknak egy-egy alkotója; legyenek ezek

a_{1}

és

a_{2}

. A

k_{1}

kör és az

a_{1}

egyenes metszéspontja legyen

T_{1}

, a

k_{2}

és

a_{2}

metszéspontja

T_{2}

. Az alkotók érintik a beírt gömböket, tehát

P T_{1}

T_{1}

pontban érinti

G_{1}

-et, és

P T_{2}

T_{2}

pontban érinti

G_{2}

-t.
Mivel a két kúp nyílásszöge ugyanakkora, a

P T_{1}

és

P T_{2}

szakaszok ugyanakkora szöget zárnak be a

Σ

síkkal. Ezért

P T_{1} = P T_{2}

. A

P

pontból tehát ugyanolyan hosszú érintőt lehet húzni a két gömbhöz, így

P

a két gömb

Φ

hatványsíkjában van.
Ezzel bebizonyítottuk, hogy

K_{1}

és

K_{2}

közös pontjai mind a

G_{1}

és

G_{2}

gömbök hatványsíkjában vannak.

Vegyük észre, hogy nem is használtuk a kúpok csúcsait; a bizonyítás változtatás nélkül működik egyköpenyű forgáshiperboloidokra⁶, ha a tengelyeik párhuzamosak, és az alkotóik ugyanakkora szöget zárnak be a tengelyekkel.
Ezt az állítást és a bizonyítást is át lehet vinni nemeuklideszi geometriákba. A párhuzamos tengelyek helyett azt kötjük ki, hogy van egy olyan

Σ

sík, amely merőlegesen elmetszi mindkét kúp tengelyét, az egyenlő nyílásszög helyett azt írjuk elő, hogy a két kúp alkotói ugyanakkora szögben döfjék

Σ

-t.
A gömbi változatban ismét csak a képzeletünk határaiba ütközünk: Hogy képzeljünk el egy gömbi kúppalástot? A hiperbolikus esetben az okozhat nehézséget, hogy a

G_{1}

és

G_{2}

gömbök nem mindig léteznek. Ezen úgy segíthetünk, ha a gömbök helyett más, állandó görbületű, de nem összezáródó felületeket, úgynevezett horoszférákat és hiperszférákat is használunk. A hiperbolikus változat továbbgondolásához további tanulásra is szükségünk van.

Ajánlott irodalom

[1]	Gömbi trigonometriáról Obádovics Gyula: Matematika c. klasszikus zsebkönyvét (5.3.12‐5.15. részek) ajánlom.

[2]	Reiman István: A geometria és határterületei c. könyve utolsó fejezetében szerepel a hiberbolikus geometria egy, a Beltrami‐Cayley‐Klein-féle modellre épülő felépítése.

[3]	H. S. M. Coxeter: A geometriák alapjai c. könyvében a 16. fejezet szól a hiperbolikus geometriákról. Itt egy rövid rész szerepel horo- és hiperciklusokról és a horoszféra geometriájáról.

Feladatok

1. Módosítsuk a békaszem-módszert; vizsgáljuk a szemgolyók helyett a két körvonal síkjait.

2. Módosítsuk a békaszem-módszert úgy, hogy a szemgolyók a körökre illeszkedő, az

O

ponton átmenő gömbök legyenek.

3. Legyenek

H_{1}

és

H_{2}

egymástól különböző körkúp vagy egyköpenyű forgáshiperboloid-felületek a térbeli derékszögű koordinátarendszerben úgy, a tengelyük párhuzamos a

z

-tengellyel, és a két felület alkotói ugyanakkora szögben döfik az

x y

koordinátasíkot. Igazoljuk, hogy két felület egyenletének különbsége lineáris függvény.

4. Bizonyítsuk be a gömbi szelőtételt.

Sose feledjük:

Ha békával találkozunk, vizsgáljuk meg a szemgolyói hatványsíkját!

¹centrális: a középpontokat összekötő egyenes

²koncentrikus: a középpontjaik egybeesnek

³Bolyai János magyar matematikus, 1802‐1860

⁴Nyikolaj Ivanovics Lobacsevszkij orosz matematikus, 1792‐1856

⁵Carl Friedrich Gauss német matematikus, 1777‐1855

⁶forgásfelület, amit úgy kaphatunk, hogy egy egyenest (a hiperboloid alkotóját) körbeforgatunk egy tőle kitérő tengely körül