Cím:	Megoldásvázlatok a 2019/7. szám emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Németh László
Füzet:	2019/november, 469 - 480. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Oldjuk meg a $\text{cos}2x=5\text{cos}x-3$ egyenletet, ha $x\in \left[-\pi ;2\pi \right]$.  (5 pont) $b)$ Oldjuk meg a valós számok halmazán a $\begin{array}{c}{\displaystyle 2\sqrt[]{\frac{x}{5}}-\sqrt[]{x+2-\sqrt[]{x+4}}\ge 0}\end{array}$ egyenlőtlenséget.  (7 pont)   Megoldás. $a)$ $\left(2\text{cos}{}^{2}x-1\right)-5\text{cos}x+3=0$; $2\text{cos}{}^{2}x-5\text{cos}x+2=0$; $\begin{array}{c}{\displaystyle {\left(\text{cos}x\right)}_{\mathrm{1,2}}=\frac{5\pm \sqrt[]{25-16}}{4}=\frac{5\pm 3}{4}\mathrm{.}}\end{array}$ ${\left(\text{cos}x\right)}_1=2$ nem lehetséges; ${\left(\text{cos}x\right)}_2=\frac{1}{2}\Rightarrow x=\pm \frac{\pi }{3}+2k\pi$, $k\in \text{Z}$. Az egyenletnek ezek közül három megoldása van az adott halmazon: $-\frac{\pi }{3}$, $\frac{\pi }{3}$, $\frac{5\pi }{3}$. $b)$ Kikötések: $x\ge 0$; $x+4\ge 0$; $x+2-\sqrt[]{x+4}\ge 0$. Ha az első teljesül, akkor a második is. Ezek teljesülését feltéve alakítsuk a harmadikat: $x+2\ge \sqrt[]{x+4}$; mindkét oldal pozitív, a négyzetre emelés ekvivalens művelet, ezért ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x^2+4x+4}& {\displaystyle \ge x+4;}\hfill \\ \hfill {\displaystyle x^2+3x}& {\displaystyle \ge 0;}\hfill \end{array}}$ ebből $x\le -3$ vagy $0\le x$ adódik. Ezt egybevetve a korábbiakkal végül $x\ge 0$ a feltétel. Rendezzük az egyenlőtlenséget: $\begin{array}{c}{\displaystyle 2\sqrt[]{\frac{x}{5}}\ge \sqrt[]{x+2-\sqrt[]{x+4}}\mathrm{.}}\end{array}$ Most is négyzetre emelhetünk, ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 4\cdot \frac{x}{5}}& {\displaystyle \ge x+2-\sqrt[]{x+4};}\hfill \\ \hfill {\displaystyle \sqrt[]{x+4}}& {\displaystyle \ge \frac{x}{5}+2;}\hfill \\ \hfill {\displaystyle x+4}& {\displaystyle \ge \frac{x^2}{25}+\frac{4}{5}x+4;}\hfill \\ \hfill {\displaystyle 0}& {\displaystyle \ge \frac{x^2}{25}-\frac{x}{5};}\hfill \\ \hfill {\displaystyle 0}& {\displaystyle \ge x^2-5x;}\hfill \end{array}}$ ebből $0\le x\le 5$ következik, ami a kikötéseknek is megfelel. Tehát a megoldás: $x\in \left[0;5\right]$.   2. Vizsgáljuk meg az $a_n=\frac{2n-3}{n+1}$, $n\in {\text{Z}}^{+}$ sorozatot korlátosság, monotonitás és konvergencia szempontjából. Megállapításainkat igazoljuk.  (11 pont)   Megoldás. A sorozat korlátos, mert alulról pl. a $-1$, felülről a 2 korlátja. $\frac{2n-3}{n+1}>-1$; $n+1>0$, tehát $2n-3>-\left(n+1\right)$; $3n>2$, ami igaz, ide ekvivalens lépéseken keresztül jutottunk, ezért a kiinduló állítás is igaz. $\begin{array}{c}{\displaystyle \frac{2n-3}{n+1}<2;2n-3<2n+2;-3<2}\end{array}$ (indoklás ugyanaz, mint az előbb). A sorozat szigorúan monoton növő, azaz $a_n<a_{n+1}$ minden $n\in {\text{Z}}^{+}$ esetén. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{2n-3}{n+1}}& {\displaystyle <\frac{2\left(n+1\right)-3}{\left(n+1\right)+1};}\hfill \\ \hfill {\displaystyle \left(2n-3\right)\left(n+2\right)}& {\displaystyle <\left(2n-1\right)\left(n+1\right);}\hfill \\ \hfill {\displaystyle 2n^2+n-6}& {\displaystyle <2n^2+n-1;}\hfill \\ \hfill {\displaystyle -6}& {\displaystyle <-1}\hfill \end{array}}$ (ismét egy mindig igaz állítást kaptunk, $\text{...}$). A sorozat konvergens, határértéke 2. $\begin{array}{c}{\displaystyle a_n=\frac{n(2-\frac{3}{n})}{n(1+\frac{1}{n})}=\frac{2-\frac{3}{n}}{1+\frac{1}{n}}\mathrm{.}}\end{array}$ Tudjuk, hogy $\underset{n\to \infty }{\overset{}{\text{lim}}}\frac{1}{n}=0$, a konvergens sorozatokra vonatkozó tételek szerint a $3\cdot \frac{1}{n}$ sorozat határértéke $3\cdot 0=0$; a számlálóé 2, a nevezőé 1, így a hányadosé 2 lesz. Ha az $\epsilon >0$, $n_0$-os definíciót használjuk, akkor a megsejtett 2 határértékkel felírhatjuk, hogy $\begin{array}{c}{\displaystyle \left|2-\frac{2n-3}{n+1}\right|<\epsilon ;\frac{5}{n+1}<\epsilon ;\frac{5}{\epsilon }-1<n;}\end{array}$ amiből $\epsilon \ge 5$ esetén $n_0=1$, egyébként $n_0=\left[\frac{5}{\epsilon }-1\right]$ (a $\left[\right]$ egészrészt jelent), tehát van minden pozitív $\epsilon$-hoz küszöbindex.   3. Egy baráti társaságban $32$ lapos magyar kártyával játszottak. (Itt a ,,színek'': piros, zöld, makk, tök; mindegyik színen belül ász, király, felső, alsó, tízes, kilences, nyolcas, hetes lapok találhatók.) Egyik este Károly feljegyezte, hogy az első tíz osztás alkalmából hány piros lapot kapott. Az 1, 3, 0, 2, 4, 2, 5, 3, 2, 4 adatokat írta fel. $a)$ Mennyi az átlag, módusz, medián, szórás?  (4 pont) Egyszer a piros lap előfordulásának törvényszerűségeit vizsgálták úgy, hogy a jól megkevert pakliból találomra kihúztak egy lapot, feljegyezték, hogy piros-e vagy sem, majd visszatették a többi közé. Ezt összesen nyolcszor végezték el. $b)$ Mennyi a valószínűsége, hogy legfeljebb $5$-ször kaptak pirosat?  (6 pont) Később megváltoztatták a húzás módját, ekkor egyszerre vettek ki $8$ lapot a megkevert pakliból. $c)$ Mennyi a valószínűsége, hogy legalább $6$ piros lap van közöttük?  (3 pont)   Megoldás. $a)$ Az átlag 2,6; módusz 2; medián 2,5; szórás 1,43. $b)$ A piros húzásának esélye: $p=\frac{1}{4}$; nem pirosé: $q=\frac{3}{4}$. Jelölje $\xi$ azt, hogy hányszor lett piros a húzás eredménye. Kevesebb számolással kapjuk a komplementer esemény valószínűségét, így ezt számítjuk ki először (négy tizedesjegyre kerekítünk). $P\left(\xi =6\right)=\left(\genfrac{}{}{0ex}{}{8}{6}\right)(\frac{1}{4}{)}^6(\frac{3}{4}{)}^2=0\mathrm{,}0038$, $P\left(\xi =7\right)=\left(\genfrac{}{}{0ex}{}{8}{7}\right)(\frac{1}{4}{)}^7\frac{3}{4}=0\mathrm{,}0004$, $P\left(\xi =8\right)=(\frac{1}{4}{)}^8=0\mathrm{,}0000$; ezek összege: 0,0042, tehát az esemény valószínűsége $P\left(A\right)=1-0\mathrm{,}0042=0\mathrm{,}9958$. $\begin{array}{c}{\displaystyle P\left(B\right)=\frac{\left(\genfrac{}{}{0ex}{}{8}{6}\right)\left(\genfrac{}{}{0ex}{}{24}{2}\right)}{\left(\genfrac{}{}{0ex}{}{32}{8}\right)}+\frac{\left(\genfrac{}{}{0ex}{}{8}{7}\right)\left(\genfrac{}{}{0ex}{}{24}{1}\right)}{\left(\genfrac{}{}{0ex}{}{32}{8}\right)}+\frac{\left(\genfrac{}{}{0ex}{}{8}{8}\right)\left(\genfrac{}{}{0ex}{}{24}{0}\right)}{\left(\genfrac{}{}{0ex}{}{32}{8}\right)}=\frac{7921}{10518300}=0\mathrm{,}0008.}\end{array}$ (*)   4. $a)$ Van-e olyan másodfokú egyenlet, amelynek egyik gyöke racionális, a másik irracionális szám?  (3 pont) $b)$ Van-e olyan egész együtthatós másodfokú egyenlet, amelynek egyik gyöke racionális, a másik irracionális szám?  (6 pont) $c)$ Van-e olyan egyszerű gráf, amelynek $8$ pontja és $29$ éle van?  (3 pont) Ha az előbbi kérdésekre igen a válasz, adjunk példát ilyen esetre, ha nem, indokoljuk a választ. $d)$ Mutassuk meg, hogy az $A$, $B$ kijelentések tetszőleges logikai értéke esetén $A\vee \left(A^B\right)=A$.  (3 pont)   Megoldás. $a)$ Igen, pl. $\left(x-1\right)\left(x-\sqrt[]{2}\right)=0$; felbontva, rendezve: $\begin{array}{c}{\displaystyle x^2-\left(1+\sqrt[]{2}\right)x+\sqrt[]{2}=0;}\end{array}$ vagy pl. $x\left(x-\pi \right)=0$; $x^2-\pi x=0$ stb. $b)$ Nincs ilyen egyenlet. Először belátjuk, hogy egy racionális és egy irracionális szám összege irracionális szám. Tegyük fel, hogy $q_1+q^{*}=q_2$; $q^{*}=q_2-q_1$; ez azonban ellentmondás, mert a racionális számok halmaza a négy alapműveletre nézve zárt halmaz, azaz két racionális szám különbsége is racionális. Az általános másodfokú egyenlet együtthatói és gyökei közötti egyik összefüggés szerint $x_1+x_2=-\frac{b}{a}$. Tegyük fel, hogy az egyik gyök racionális, a másik irracionális, ekkor a bal oldal irracionális, a jobb oldal racionális, ami lehetetlen. $c)$ Nincs ilyen gráf. Ha a gráf egyszerű teljes gráf volna, akkor $\left(\genfrac{}{}{0ex}{}{8}{2}\right)=28$ éle lenne. Mivel 29 éle van, legalább egy hurokélnek kell lennie, ekkor viszont nem egyszerű a gráf. $d)$ Készítsük el az igazság táblázatot:   ${\displaystyle \begin{array}{|cccc|}\hline \hfill {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>}}\hfill & \hfill {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math>}}\hfill & \hfill {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mo>^</mo><mi>B</mi></math>}}\hfill & \hfill {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mo>∨</mo><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>A</mi><mo>^</mo><mi>B</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math> }}\hfill \\ \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i }}\hfill \\ \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ i }}\hfill \\ \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h }}\hfill \\ \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h }}\hfill \\ \hline\end{array}}$   Láthatjuk, hogy az első és utolsó oszlop rendre egyezik, ezzel az állítást igazoltuk.   II. 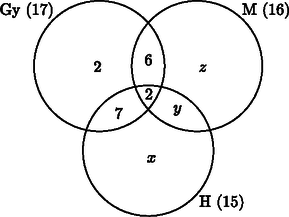rész     5. Nyári vitorlástábor $26$ fiataljának úszásoktatást szerveztek fizikai erőnlétük javítása, vízi biztonságuk erősítése céljából. A táborban gyors-, mell- és hátúszás oktatására volt szakképzett oktató, így a résztvevők e három úszásnemre jelentkezhettek. Mindenkinek legalább egyet választania kellett. $17$-en választották a gyorsúszást, $15$-en jelentkeztek hátúszásra, $16$-an pedig mellúszásra. $8$ olyan, gyorsúszást választott fiatal van, aki hátúszásra nem jelentkezett. Azok közül, akik a gyorsot választották, $8$-an mellre is jelentkeztek. Csupán ketten választották mindhárom úszásnemet. $a)$ Hány résztvevő választotta a mell- és hátúszást is?  (7 pont) Az oktatás végén a balatonboglári uszodában versenyt rendeztek a táborlakók számára. A leány mellúszás döntőjébe Anna, Bea, Cecília, Dóra, Edit és Flóra került. $b)$ Hányféleképpen végződhetett a döntő, ha tudjuk, Dóra nem lett dobogós (nem volt az első háromban), de nem is lett utolsó, továbbá Bea megelőzte Flórát, azonban kikapott Edittől? Holtverseny nem volt.  (6 pont) A táborzáró estén díjak, jutalmak átadására került sor. A szponzorok három értékes tárgyat sorsolással kívántak kiosztani, ezért a táborozók nevét felírták egy-egy cédulára és ezeket egy urnába dobták, majd a főszponzor kihúzott három cédulát. $c)$ Mennyi a valószínűsége annak, hogy mindhárom nyertes csak egy úszásnem oktatásán vett részt?  (3 pont)   Megoldás. $a)$ A leírásban szereplő adatok alapján elkészíthetjük a mellékelt ábrát, ahol az ismeretlen részhalmazok elemeinek számát $x$, $y$, $z$ jelöli. Felírhatjuk az alábbi egyenleteket: ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle x+y}& {\displaystyle =6}\hfill \\ \hfill {\displaystyle y+z}& {\displaystyle =8}\hfill \\ \hfill {\displaystyle \left(x+y\right)+z}& {\displaystyle =9}\hfill \end{array}}\}\Rightarrow 6+z=9\Rightarrow }\hfill \\ \hfill {\displaystyle \Rightarrow z=\mathrm{3,}y=\mathrm{5,}x=1.}\hfill \end{array}}$     Tehát a mell- és hátúszást is 7 résztvevő választotta. $b)$ Dóra 4., vagy 5. lett. Tegyük fel, hogy Dóra negyedik helyezett lett. Edit, Bea és Flóra egymáshoz képest ilyen sorrendben következtek, tehát ha kiválasztjuk a maradék öt helyezésből azt a hármat, amelyikre őket tesszük, akkor a fennmaradó két helyen Anna és Cecília osztozik. A három hely kiválasztása $\left(\genfrac{}{}{0ex}{}{5}{3}\right)=10$-féleképpen lehetséges, Anna és Cecília kétféleképpen helyezkedhetnek el, így ebben az esetben 20 lehetőség adódik. Ugyanez a helyzet akkor is, ha Dóra ötödik lett. Tehát a döntő 40-féleképpen végződhetett. $c)$ Összesen 6 olyan fiatal volt, aki csak egy úszásnem oktatásán vett részt, közülük $\left(\genfrac{}{}{0ex}{}{6}{3}\right)=20$-féleképpen választhatjuk ki a három nyertest (sorrend nem számít, hiszen nem ismétlődhetnek), míg az összes lehetőség $\left(\genfrac{}{}{0ex}{}{26}{3}\right)=2600$, tehát $\begin{array}{c}{\displaystyle P\left(A\right)=\frac{20}{2600}=\frac{1}{130}=0\mathrm{,}0077.}\end{array}$   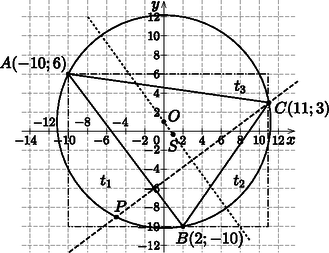6. Az $ABC$ háromszög csúcsainak koordinátái: $A\left(-10;6\right)$, $B\left(2;-10\right)$, $C\left(11;3\right)$. $a)$ Írjuk fel a háromszög körülírt körének egyenletét.  (4 pont) $b)$ Jelölje $O$ a körülírt kör középpontját, $S$ a súlypontot. Írjuk fel az $OS$ egyenes egyenletét. Milyen helyzetű az $OS$ egyenes az $AB$ egyeneshez viszonyítva? Igazoljuk észrevételünket.  (4 pont) $c)$ Hol van a $C$-n átmenő magasságvonal és a körülírt kör $C$-től különböző metszéspontja?  (4 pont) $d)$ Mekkora a háromszög területe?  (4 pont)   Megoldás. $a)$ I. megoldás. A kör egyenlete ${\left(x-u\right)}^2+{\left(y-v\right)}^2=R^2$, ahol $O\left(u;v\right)$ a kör középpontja, $R$ a sugara.     ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle {\left(-10-u\right)}^2+{\left(6-v\right)}^2}& {\displaystyle =R^2\mathrm{,}}\hfill & \text{(<mi>*</mi>)}\\ \hfill {\displaystyle *{\left(2-u\right)}^2+{\left(-10-v\right)}^2}& {\displaystyle =R^2\mathrm{,}}\hfill & \text{(<mi>*</mi>)}\\ \hfill {\displaystyle {\left(11-u\right)}^2+{\left(3-v\right)}^2}& {\displaystyle =R^2;\text{felbontva}}\hfill & \text{(<mi>*</mi>)}\\ \hfill {\displaystyle u^2+v^2+20u-12v+136}& {\displaystyle =R^2\mathrm{,}}\hfill & \text{(<mi>*</mi>)}\\ \hfill {\displaystyle u^2+v^2-4u+20v+104}& {\displaystyle =R^2\mathrm{,}}\hfill & \text{(<mi>*</mi>)}\\ \hfill {\displaystyle u^2+v^2-22u-6v+130}& {\displaystyle =R^2\mathrm{,}}\hfill & \text{(<mi>*</mi>)}\\ \hfill {\displaystyle 24u-32v+32}& {\displaystyle =0\Rightarrow 3u=4v-\mathrm{4,}}\hfill & \text{(<mi>*</mi>)}\\ \hfill {\displaystyle -18u-26v+26}& {\displaystyle =\mathrm{0,}}\hfill & \text{(<mi>*</mi>)}\\ \hfill {\displaystyle -6\left(4v-4\right)-26v+26}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle -24v+24-26v+26}& {\displaystyle =0;50v=50;}\hfill \end{array}}$ $v=1$; $3u=4-4$; $u=0$; $O\left(0;1\right)$; $R^2=125$. A körülírt kör egyenlete : $x^2+{\left(y-1\right)}^2=125$. II. megoldás. Az oldalak felezőmerőlegeseit felírva (bármelyik kettőt), a belőlük alkotott egyenletrendszer megoldása a körülírt kör középpontjának koordinátáit eredményezi. Ezt bármelyik csúccsal összekötve, a kapott szakasz hossza adja a kör sugarát. Az $a$ oldal felezőmerőlegesének egyenlete: $9x+13y=13$; a $b$ oldal felezőmerőlegesének egyenlete: $7x-y=-1$; a $c$ oldal felezőmerőlegesének egyenlete: $3x-4y=-4$. $O\left(0;1\right)$, $R=5\sqrt[]{5}$. $b)$ A háromszög súlypontja ${\displaystyle \begin{array}{c}\hfill {\displaystyle S\left(\frac{-10+2+11}{3};\frac{6-10+3}{3}\right);S\left(1;-\frac{1}{3}\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \overrightarrow{OS}\left(1-0;-\frac{1}{3}-1\right);\overrightarrow{OS}\left(1;-\frac{4}{3}\right)\mathrm{.}}\hfill \end{array}}$ Használjuk irányvektornak az $\overrightarrow{OS}$-sel párhuzamos $\text{v}\left(3;-4\right)$ vektort, pontnak $O$-t, így az $OS$ egyenes egyenlete: $\begin{array}{c}{\displaystyle v_{2}x-v_{1}y=v_2{x}_0-v_1{y}_0;-4x-3y=0-3;4x+3y=3.}\end{array}$ Az $OS$ egyenes (Euler-egyenes) párhuzamos $AB$-vel, mert $\overrightarrow{AB}\left(12;-16\right)$ párhuzamos $\overrightarrow{OS}$-sel. $c)$ A $C$-n átmenő magasságvonal merőleges $AB$-re, így a $\text{v}\left(3;-4\right)$ vektor a magasságvonal normálvektora lesz. A magasságvonal egyenlete: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle n_{1}x+n_{2}y}& {\displaystyle =n_1{x}_0+n_2{y}_0;}\hfill \\ \hfill {\displaystyle 3x-4y}& {\displaystyle =33-12.}\hfill \end{array}}$ Innen $y=\frac{3}{4}x-\frac{21}{4}$, ezt beírva a körülírt kör egyenletébe: $\begin{array}{c}{\displaystyle x^2+{\left(\frac{3}{4}x-\frac{21}{4}-1\right)}^2=125.}\end{array}$ Összevonás, négyzetre emelés után az $\begin{array}{c}{\displaystyle x^2+\frac{9}{16}{x}^2-\frac{150}{16}x+\frac{625}{16}=125}\end{array}$ egyenletet kapjuk. 16-tal szorozva, 25-tel osztva az $x^2-6x-55=0$ egyenlethez jutunk. Ebből $\begin{array}{c}{\displaystyle x_{\mathrm{1,2}}=\frac{6\pm \sqrt[]{36+220}}{2}=\frac{6\pm 16}{2}\mathrm{,}}\end{array}$ $x_1=11$, ez a $C$ pont abszcisszája, $x_2=-5$; $y_2=\frac{3}{4}\left(-5\right)-\frac{21}{4}=-9$; tehát $P\left(-5;-9\right)$.$$ $d)$ A területet a legegyszerűbben úgy kaphatjuk meg, hogy téglalapba foglaljuk a háromszöget és levágjuk a felesleget. A téglalap vízszintes oldala 21 egység, a függőleges 16 egység, így területe 336 területegység. $\begin{array}{c}{\displaystyle t_1=\frac{16\cdot 12}{2}=96;t_2=\frac{9\cdot 13}{2}=58\mathrm{,}5;t_3=\frac{21\cdot 3}{2}=31\mathrm{,}5;}\end{array}$ tehát a háromszög területe: $T=336-\left(96+58\mathrm{,}5+31\mathrm{,}5\right)=150$ területegység. További megoldások is vannak, nézzünk vázlatosan néhányat. I. Meghatározzuk $AB$ egyenletét, ez: $4x+3y=-22$, összekapcsolva a $C$-n átmenő magasságvonal $3x-4y=21$ egyenletével, a megoldás a magasság talppontjának koordinátáit eredményezi: $T\left(-1;-6\right)$. Az $AB$ hossza 20, a $TC$ hossza 15 egység, innen a terület $150$ területegység. II. Koszinusz tétellel kiszámítjuk az $A$ csúcsnál levő szöget, erre ${45}^{\circ }$ adódik, alkalmazzuk a trigonometrikus területképletet: $\begin{array}{c}{\displaystyle T=\frac{20\cdot 15\sqrt[]{2}\cdot \frac{\sqrt[]{2}}{2}}{2}=150.}\end{array}$ III. Használjuk a Heron-képletet. Sok számolással jár, ugyanezt az eredményt adja.   7. Egy mértani sorozat első négy tagjából rendre $1$-et, $2$-t, $5$-öt, $11$-et elvéve egy számtani sorozat négy szomszédos tagját kapjuk. $a)$ Mennyi a mértani sorozat első tagja és hányadosa?  (8 pont) Számítsuk ki az adott eljárással a számtani sorozat elemeit, majd képzeletben folytassuk mindkét irányba a sorozatot. $b)$ Van-e ebben a számsorban olyan szomszédos elemekből álló rész, amelyben az elemek összege $2019?$ Ha igen, adjuk meg az összes megoldást. Indokoljuk a választ.  (8 pont)   Megoldás. $a)$ A mértani sorozat első négy tagja: $a$, $aq$, $a{q}^2$, $a{q}^3$. Az alakítás utáni számtani sorozat elemei: $a-1$; $aq-2$; $a{q}^2-5$; $a{q}^3-11$. Tudjuk, hogy a számtani sorozat $n$-edik elemére $a_n=\frac{a_{n-1}+a_{n+1}}{2}$ $\left(n\ge 2\right)$ teljesül, ezért felírhatjuk az alábbi egyenleteket: ${\displaystyle \begin{array}{cccccc}\hfill {\displaystyle 2\left(aq-2\right)}& {\displaystyle =\left(a-1\right)+\left(a{q}^2-5\right)}\hfill & {\displaystyle \Rightarrow 0}\hfill & \hfill {\displaystyle =a{q}^2-2aq+a-2}& {\displaystyle \Rightarrow 2}\hfill & {\displaystyle =a{\left(q-1\right)}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle 2\left(a{q}^2-5\right)}& {\displaystyle =\left(aq-2\right)+\left(a{q}^3-11\right)}\hfill & {\displaystyle \Rightarrow 0}\hfill & \hfill {\displaystyle =a{q}^3-2a{q}^2+aq-3}& {\displaystyle \Rightarrow 3}\hfill & {\displaystyle =aq{\left(q-1\right)}^2\mathrm{.}}\hfill \end{array}}$ Ez utóbbiban az $a{\left(q-1\right)}^2$-t 2-vel helyettesítve $3=2q$-t kapunk,   amiből $q=\frac{3}{2}$, ezt felhasználva $2=a(\frac{3}{2}-1{)}^2$, ebből $a=8$. A mértani sorozat első tagja 8, hányadosa $\frac{3}{2}$. Ellenőrzés: a mértani sorozat első négy tagja: 8; 12; 18; 27, ezekből a levonások után 7; 10; 13; 16 lesz, amely számok közötti különbség mindenütt 3, azaz egy számtani sorozat (amely csupa egész számból áll) négy szomszédos eleme. $b)$ $\text{...}\mathrm{,}-\mathrm{5,}-\mathrm{2,1,4,}\text{7, 10, 13, 16}\mathrm{,19,22,25,28,}\text{...}\mathrm{.}$ Tegyük fel, hogy van ilyen rész, az első tagját jelöljük $b$-vel, a benne szereplő tagok számát $k$-val. Ekkor $\begin{array}{c}{\displaystyle b+\left(b+3\right)+\left(b+6\right)+\text{...}+\left[b+\left(k-1\right)3\right]=2019.}\end{array}$ Használjuk az összegképletet: $k\frac{b+b+\left(k-1\right)3}{2}=2019$; $k(b+\frac{k-1}{2}3)=2019$ $\left(k\in {\text{Z}}^{+}\right)$. Mivel $2019=3\cdot 673$, ezért $k$ lehetséges értéke 1, 3, 673, 2019, az ezekhez tartozó második tényező rendre 2019, 673, 3, 1. ${\displaystyle \begin{array}{cccccccc}\hfill {\displaystyle k}& {\displaystyle =\mathrm{1,}}\hfill & {\displaystyle b+\frac{1-1}{2}\cdot 3}\hfill & \hfill {\displaystyle =2019}& {\displaystyle \Rightarrow }\hfill & {\displaystyle }\hfill & \hfill {\displaystyle b}& {\displaystyle =\mathrm{2019,}}\hfill \\ \hfill {\displaystyle k}& {\displaystyle =\mathrm{3,}}\hfill & {\displaystyle b+\frac{3-1}{2}\cdot 3}\hfill & \hfill {\displaystyle =673}& {\displaystyle \Rightarrow }\hfill & {\displaystyle }\hfill & \hfill {\displaystyle b}& {\displaystyle =\mathrm{670,}}\hfill \\ \hfill {\displaystyle k}& {\displaystyle =\mathrm{673,}}\hfill & {\displaystyle b+\frac{673-1}{2}\cdot 3}\hfill & \hfill {\displaystyle =3}& {\displaystyle \Rightarrow }\hfill & {\displaystyle }\hfill & \hfill {\displaystyle b}& {\displaystyle =-\mathrm{1005,}}\hfill \\ \hfill {\displaystyle k}& {\displaystyle =\mathrm{2019,}}\hfill & {\displaystyle b+\frac{2019-1}{2}\cdot 3}\hfill & \hfill {\displaystyle =1}& {\displaystyle \Rightarrow }\hfill & {\displaystyle }\hfill & \hfill {\displaystyle b}& {\displaystyle =-3026.}\hfill \end{array}}$ Szerepelnek-e ezek a számok a számsorban? Ha a 670, illetve 2019 benne volna, akkor a négy számtól ‐ a felsorolás szerint ‐ jobbra lenne, a 7-től az $n$-edik helyen. $670=7+n\cdot 3\Rightarrow n=221$; $2019=7+n\cdot 3\Rightarrow n=670\mathrm{,}\dot{6}\notin {\text{Z}}^{+}$. Azt kaptuk, hogy a 670 tagja a számsornak, a 2019 pedig nem ($670+673+676=2019$). Ugyanígy járhatunk el a két másik $b$-vel, ezek balra vannak, tehát $-1005=7+n\left(-3\right)\Rightarrow n=337\mathrm{,}\dot{3}\notin {\text{Z}}^{+}$; $-3026=7+n\left(-3\right)\Rightarrow n=1011$, azaz a $-1005$ nincs a számok között, a $-3026$ viszont igen (7-től balra az 1011. helyen). Ez utóbbi esetben a $-3026$-tól kezdve 2019 számot véve a számsorból, ezek összege is 2019 lesz: $\begin{array}{c}{\displaystyle 2019\frac{\left[-3026+\left(-3026+2018\cdot 3\right)\right]}{2}=2019\frac{-3026+3028}{2}=2019.}\end{array}$ Tehát van a számsorban két olyan rész, amelyben a szomszédos tagok összege 2019.   Megjegyzés: a 670, 673, 676 számhármasra viszonylag könnyen rá lehet jönni, mert a 2019 szorzattá bontásakor a $3\cdot 673$-at kapjuk, tehát csak azt kell megnézni, hogy a 673 benne van-e a számsorban. Ha ugyanis igen, akkor a 3-as differencia miatt a két szomszédja is, és ennek a három számnak az összege 2019. Mint tudjuk, a 673 benne van a számsorban. A másikra a számsor ($\text{...}\mathrm{,}-\mathrm{11,}-\mathrm{8,}-\mathrm{5,}-\mathrm{2,1,4,7,10,13,}\text{...}$) 1 elemének szomszédjait összeadva jöhetünk rá, ugyanis 2-t kapunk eredményül; ha a második szomszédokat adjuk össze, szintén 2 lesz az eredmény, és így tovább. Ilyen módon 1009 párt képezve, majd a végén az 1-et hozzáadva 2019-et kapunk. Könnyen kiszámítható, hogy a legtávolabbi pár bal vége $-3026$, a jobb vége pedig 3028. Ezek után természetesen igazolni kellene, hogy további megoldások nincsenek.   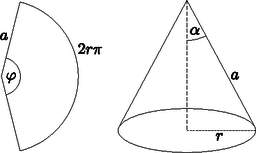8. Egységsugarú körből megfelelő körcikket kivágva, majd egyenes körkúp palástjának kialakítva tölcsért készítünk. $a)$ Mekkora a körcikk középponti szöge, ha a tölcsér térfogata a lehető legnagyobb?  (9 pont) Rendelkezésre áll egy $10\times 16$ egység oldalú téglalap alakú lemez, amelyből az $a)$ részben kapott maximális térfogatú tölcséreket szeretnénk kialakítani. $b)$ Tudunk-e ebből a lemezből $50$ db ilyen tölcsért csinálni? Megállapításunkat indokoljuk.  (7 pont)   Megoldás. $a)$ I. megoldás. Legyen a kúp félnyílásszöge $\alpha$, ekkor az alapkör sugara $r=\text{sin}\alpha$, magassága $m=\text{cos}\alpha$, térfogata $V=\frac{\pi \text{sin}{}^2\alpha \cdot \text{cos}\alpha }{3}$, ${\displaystyle \begin{array}{cc}\hfill {\displaystyle V\text{'}\left(\alpha \right)}& {\displaystyle =\frac{\pi }{3}\left[2\text{sin}\alpha \text{cos}{}^2\alpha +\text{sin}{}^2\alpha \left(-\text{sin}\alpha \right)\right]=\frac{\pi }{3}\left[2\text{sin}\alpha \left(1-\text{sin}{}^2\alpha \right)-\text{sin}{}^3\alpha \right]=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{\pi }{3}\left(2\text{sin}\alpha -3\text{sin}{}^3\alpha \right)\mathrm{.}}\hfill \end{array}}$ Ahol az első derivált 0, ott lehet szélsőértéke a függvénynek: $\begin{array}{c}{\displaystyle 0=\text{sin}\alpha \left(2-3\text{sin}{}^2\alpha \right)\mathrm{.}}\end{array}$ I. eset. $\text{sin}\alpha =0\Rightarrow \alpha =0$, ez nem lehet maximumhely. II. eset. ${\displaystyle \begin{array}{c}\hfill {\displaystyle 0=2-3\text{sin}{}^2\alpha \Rightarrow \text{sin}\alpha =\sqrt[]{\frac{2}{3}}\Rightarrow \alpha =54\mathrm{,}{74}^{\circ }\left(0<\alpha <{90}^{\circ }\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle V\text{'}\text{'}\left(\alpha \right)=\frac{\pi }{3}\left(2\text{cos}\alpha -9\text{sin}{}^2\alpha \text{cos}\alpha \right)=\frac{\pi }{3}\text{cos}\alpha \left(2-9\frac{2}{3}\right)<\mathrm{0,}}\hfill \end{array}}$ itt tehát valóban maximuma van a térfogatnak. Ekkor a körcikk középponti szöge ($\phi )$: $\phi \cdot 1=2r\pi$; $\phi =2\pi \sqrt[]{\frac{2}{3}}\approx 5\mathrm{,}13$. A legnagyobb térfogatú tölcsérhez tartozó körcikk középponti szöge $293\mathrm{,}{93}^{\circ }$. II. megoldás. Az egyenes körkúp félnyílásszöge és kiterített palástjának középponti szöge között összefüggés van. Egyrészt $\phi \cdot a=2r\pi$, másrészt $\begin{array}{c}{\displaystyle \text{sin}\alpha =\frac{r}{a}\Rightarrow \phi a=2\pi a\text{sin}\alpha \Rightarrow \phi =2\pi \text{sin}\alpha \mathrm{,}}\end{array}$ innen     $\begin{array}{c}{\displaystyle \text{sin}\alpha =\frac{\phi }{2\pi }\mathrm{,}\text{cos}\alpha =\sqrt[]{1-{\left(\frac{\phi }{2\pi }\right)}^2}\mathrm{.}}\end{array}$ A térfogatfüggvény: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle V\left(\phi \right)}& {\displaystyle =\frac{\pi }{3}{\left(\frac{\phi }{2\pi }\right)}^2\sqrt[]{1-{\left(\frac{\phi }{2\pi }\right)}^2}=\frac{\pi }{3}\frac{{\phi }^2}{4{\pi }^2}\frac{\sqrt[]{4{\pi }^2-{\phi }^2}}{2\pi }=\frac{1}{24{\pi }^2}\sqrt[]{4{\pi }^2{\phi }^4-{\phi }^6}=}\hfill \\ \hfill {\displaystyle *}& {\displaystyle =\frac{1}{24\sqrt[]{2}{\pi }^2}\sqrt[]{8{\pi }^2{\phi }^4-2{\phi }^6}\mathrm{.}}\hfill \end{array}}$ Mivel a négyzetgyök függvény szigorúan monoton nő, ezért elég meghatározni a gyökjel alatti mennyiség maximumát. Ezt megoldhatjuk elemi úton is: $\begin{array}{c}{\displaystyle {\phi }^2{\phi }^2\left(8{\pi }^2-2{\phi }^2\right)=8{\pi }^2{\phi }^4-2{\phi }^6\mathrm{,}}\end{array}$ a számtani-mértani közép közötti összefüggést használva kapjuk, hogy $\begin{array}{c}{\displaystyle \frac{{\phi }^2+{\phi }^2+\left(8{\pi }^2-2{\phi }^2\right)}{3}\ge \sqrt[3]{{\phi }^2{\phi }^2\left(8{\pi }^2-2{\phi }^2\right)};\frac{8{\pi }^2}{3}\ge \sqrt[3]{{\phi }^2{\phi }^2\left(8{\pi }^2-2{\phi }^2\right)}\mathrm{.}}\end{array}$ A bal oldal állandó, a jobb oldali mennyiség akkor lesz a legnagyobb, ha az egyenlőség teljesül, ez pedig csak a tényezők egyenlősége esetén valósul meg (a köbgyök függvény is szigorúan monoton növekvő). $\begin{array}{c}{\displaystyle 8{\pi }^2-2{\phi }^2={\phi }^2\Rightarrow 8{\pi }^2=3{\phi }^2\Rightarrow \phi =2\pi \sqrt[]{\frac{2}{3}}\mathrm{,}}\end{array}$ ami $293\mathrm{,}{93}^{\circ }$-nak felel meg. 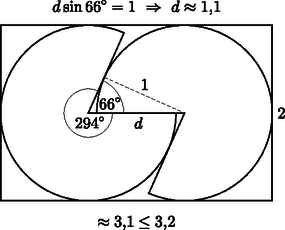$b)$ Az hamar belátható, hogy egységsugarú körökből nem lehet kivágni 50 db-ot az adott méretű lemezből. (Ellenőrizhető, hogy legfeljebb 41 kör fér el a $10\times 16$-os téglalapon.) Azonban két ‐ a legnagyobb térfogatot eredményező ‐ körcikk befoglalható egy $2\times 3\mathrm{,}2$ egység oldalú téglalapba az ábrának megfelelően. $16:3\mathrm{,}2=5$, $10:2=5$, ezért a lemezből kivágható 25 db ilyen kis téglalap, mindegyikben 2 körcikkel, tehát tudunk 50 db tölcsért készíteni.       9. Adott az $f\left(x\right)=\text{cos}x$ és a $g\left(x\right)=\text{sin}2x$ függvény $\left(x\in \text{R}\right)$. $a)$ Írjuk fel a $h\left(x\right)=f\circ g$, illetve $k\left(x\right)=g\circ f$ függvényeket, állapítsuk meg az értékkészletüket.  (6 pont) $b)$ Hol metszi egymást az $f\left(x\right)$ és $g\left(x\right)$ függvény grafikonja? Adjuk meg a metszéspontok koordinátáit.  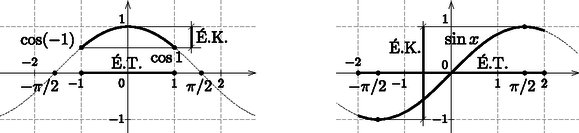(5 pont) $c)$ Mekkora e két görbe által közrefogott síkidom területe, ha $x\in [-\frac{\pi }{2};\frac{\pi }{2}]?$   (5 pont)   Megoldás. $a)$ $h\left(x\right)=f\circ g=\text{cos}\left(\text{sin}2x\right)$; $k\left(x\right)=g\circ f=\text{sin}\left(2\text{cos}x\right)$. Mindkét esetben a belső függvény értékkészlete lesz a külső függvény értelmezési tartománya.     $h\left(x\right)$ esetén: $-1\le \text{sin}2x\le 1$; $\text{cos}\left(-1\right)=\text{cos}1$, ezért $\text{cos}1\le h\left(x\right)\le 1$, más jelöléssel $h\left(x\right)\in \left[\text{cos}1;1\right]$. $k\left(x\right)$ esetén: $-2\le 2\text{cos}x\le 2$, ennek részhalmaza $a[-\frac{\pi }{2};\frac{\pi }{2}]$, ahol a $\text{sin}x$ $-1$-től $+1$-ig minden valós értéket felvesz, így $-1\le k\left(x\right)\le 1$, vagy $k\left(x\right)\in \left[-1;1\right]$. 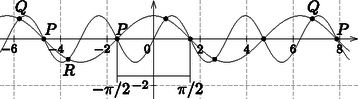$b)$ A metszéspontok abszcisszája a $\text{cos}x=\text{sin}2x$ egyenlet megoldása. $\begin{array}{c}{\displaystyle \text{cos}x=2\text{sin}x\cdot \text{cos}x;0=\text{cos}x\left(2\text{sin}x-1\right);\text{cos}x=0\Rightarrow x_1=\frac{\pi }{2}+p\pi \mathrm{,}p\in \text{Z};}\end{array}$ vagy $2\text{sin}x-1=0\Rightarrow \text{sin}x=\frac{1}{2}$. Innen $x_2=\frac{\pi }{6}+2q\pi$, $q\in \text{Z}$, illetve $x_3=\frac{5\pi }{6}+2r\pi$, $r\in \text{Z}$. Ezekhez tartozó ordináták rendre: $y_1=0$; $y_2=\frac{\sqrt[]{3}}{2}$; $y_3=-\frac{\sqrt[]{3}}{2}$. A metszéspontok tehát: $\begin{array}{c}{\displaystyle P\left(\frac{\pi }{2}+p\pi ;0\right)\mathrm{,}Q\left(\frac{\pi }{6}+2q\pi ;\frac{\sqrt[]{3}}{2}\right)\mathrm{,}R\left(\frac{5\pi }{6}+2r\pi ;-\frac{\sqrt[]{3}}{2}\right)\mathrm{,}p\mathrm{,}q\mathrm{,}r\in \text{Z}\mathrm{.}}\end{array}$     A trigonometrikus egyenlet II. megoldása: $\text{cos}x=\text{sin}(\frac{\pi }{2}-x)$ (pótszögek közötti összefüggés) $\text{sin}(\frac{\pi }{2}-x)=\text{sin}2x$, 1. eset: $\frac{\pi }{2}-x=2x+2k\pi$, innen $x=\frac{\pi }{6}-\frac{2k\pi }{3}$, $k\in \text{Z}$. 2. eset: $\frac{\pi }{2}-x+2x=\pi +2l\pi$, innen $x=\frac{\pi }{2}+2l\pi$, $l\in \text{Z}$. Meggyőződhetünk, hogy ezek az előbbi megoldással azonosak. $c)$ A területszámítást két részre bontjuk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle t_1}& {\displaystyle ={\int }_{-\frac{\pi }{2}}^{\frac{\pi }{6}}\left(\text{cos}x-\text{sin}2x\right)\text{d}x={\left[\text{sin}x+\frac{\text{cos}2x}{2}\right]}_{-\frac{\pi }{2}}^{\frac{\pi }{6}}=\frac{1}{2}+\frac{1}{4}-\left(-1-\frac{1}{2}\right)=\frac{9}{4};}\hfill \\ \hfill {\displaystyle t_2}& {\displaystyle ={\int }_{\frac{\pi }{6}}^{\frac{\pi }{2}}\left(\text{sin}2x-\text{cos}x\right)\text{d}x={\left[-\frac{\text{cos}2x}{2}-\text{sin}x\right]}_{\frac{\pi }{6}}^{\frac{\pi }{2}}=\frac{1}{2}-1-\left(-\frac{1}{4}-\frac{1}{2}\right)=\frac{1}{4}\mathrm{.}}\hfill \end{array}}$ $t=t_1+t_2=\frac{9}{4}+\frac{1}{4}=\frac{5}{2}$. A bezárt síkidom területe $\frac{5}{2}$.