Cím:	Térbe kilépő bizonyítások II.
Szerző(k):	Kós Géza
Füzet:	2019/november, 456 - 466. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Vetítés és inverzió Ebben a cikksorozatban olyan bizonyításokat mutatunk be, amikor a geometriai alakzatokat ,,térbe kilépve'', három- vagy akár még magasabb dimenziós objektumok vetületeként vagy metszeteként állítjuk elő. A második részben olyan példákat veszünk sorra, amikor egy síkbeli alakzatot egy másik síkra vagy egy gömbfelületre vetítünk egy pontból. Az alakzataink pontokból, egyenesekből és körvonalakból fognak állni. Az új helyzetben az ábrának további szimmetriái lesznek, és szimmetriából fog következni a bizonyítandó állítás. Többször is használni fogunk egy fontos geometriai transzformációt, az inverziót. Az inverzió legfontosabb tulajdonságait a Függelékben foglaltam össze.   Körvonal vetítése körvonalra A módszert először a következő, a cikk előző részéből is ismert tételen mutatom be.   1. példa. Ha az $ABCD$ érintőnégyszög beírt köre az $AB$, $BC$, $CD$, $DA$ oldalakat rendre az $E$, $F$, $G$, illetve $H$ pontban érinti, akkor az $AC$, $BD$, $EG$ és $FH$ szakaszok egy ponton mennek át.   A tételt az eddigi eszközeinkkel is sokféleképpen be lehet bizonyítani (lásd az 1.a‐1.c feladatokat), de most következzen inkább egy újabb térbe kilépés. Jelöljük $k$-val a beírt kört, és legyen $K$ az $EG$ és $FH$ húrok metszéspontja. Ha akkora szerencsénk van, hogy $K$ éppen a $k$ középpontja, akkor rengeteg szimmetriát láthatunk az ábrában (1. ábra). 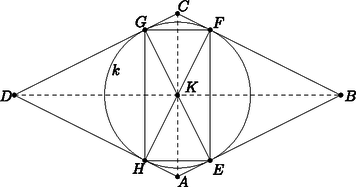    1. ábra   Az $EFGH$ négyszögben az $EG$ és $FH$ átlók a kör átmérői, a $K$ középpontban felezik egymást és egyenlő hosszúak, tehát a négyszög egy téglalap. A téglalap egyik szimmetriatengelye az $EF$ és a $GH$ oldalak közös felezőmerőlegese. Erre a tengelyre szimmetrikusak a körhöz $E$-ben és $F$-ben húzott érintők is; ezek metszéspontja, $B$ tehát rajta van a szimmetriatengelyen. Ugyanígy $D$ is, és persze a téglalap középpontja, $K$ is a tengelyen van. Ugyanezt a másik szimmetriatengelyre is elmondhatjuk, és így látjuk, hogy a $K$ ponton az $AC$ egyenes is átmegy. Az általános esetben azzal próbálkozunk, hogy az ábra $\Sigma$ síkját a térben helyezzük el, és valamilyen $O$ pontból egy másik $\Sigma \text{'}$ síkra vetítjük át. Szokás szerint a különböző alakzatok képét vesszővel jelölve, a célunk, hogy a $k$ kör képe, $k\text{'}$ az új síkon egy $K\text{'}$ középpontú körvonal legyen (2. ábra). 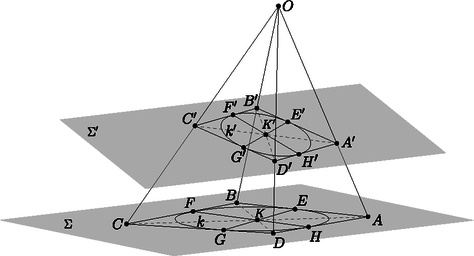    2. ábra   Ha ilyen vetítés létezik, akkor a $\Sigma \text{'}$ síkban az előbbi, szimmetrikus ábrát kapjuk meg újra, és már láttuk, hogy az $A\text{'}C\text{'}$, $B\text{'}D\text{'}$, $E\text{'}G\text{'}$, és $F\text{'}H\text{'}$ szakaszok mind átmennek a $K\text{'}$ ponton. Az $O$-ból visszavetítve a pontokat az eredeti $\Sigma$ síkra, a bizonyítandó állítást kapjuk. A bizonyításhoz szükséges vetítés mindig létezik, de ez nem magától értetődő; rövidesen mutatok rá egy lehetséges konstrukciót.   Ugyanennek az ötletnek egy másik alkalmazása a következő, néhány évvel ezelőtti KöMaL-feladat.   2. példa. Az $ABCD$ konvex érintőnégyszögbe írt kör az $AB$ és $BC$ oldalakat az $E$, illetve az $F$ pontban érinti. Az $AC$ átló a beírt kört a $P$ és a $Q$ pontban metszi; a $Q$ pont az $A$ és a $P$ pontok között helyezkedik el. Mutassuk meg, hogy a $BD$, $EP$ és $FQ$ egyenesek egy ponton mennek át. (KöMaL A. 594., 2013. szeptember)   Megoldás. Az 1. példához hasonlóan definiáljuk a $G$, $H$ és $K$ pontokat, majd az egész ábrát úgy vetítsük egy új síkra, hogy a beírt kör képe körvonal legyen, és a középpontja a $K\text{'}$ pont. A vetítés után az ábra szimmetrikus a $B\text{'}D\text{'}$ egyenesre; speciálisan az $E\text{'}P\text{'}$ és $F\text{'}Q\text{'}$ szakaszok egymás tükörképei, ezért a tükrözés tengelyét, a $B\text{'}D\text{'}$ egyenest ugyanabban a pontban metszik (3. ábra). 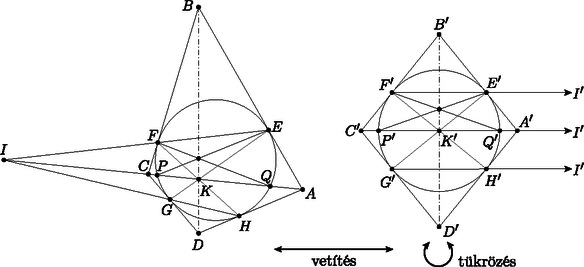    3. ábra     Az ábrán még egy érdekes pontot megjelöltem: az $I$ pont az $EF$ és $GH$ egyenesek metszéspontja. A vetítés után ezek képei, az $E\text{'}F\text{'}$ és $G\text{'}H\text{'}$ párhuzamosak az $A\text{'}C\text{'}$ egyenessel, és könnyű meggondolni, hogy a vetítéshez használt $OI$ egyenes is párhuzamos velük. Ezért az $I\text{'}$ pont nem jön létre, vagy pedig úgy is mondhatjuk, hogy ‐ a $\Sigma \text{'}$ síkot projektív értelemben kiterjesztve ‐ $I\text{'}$ ezeknek az egyeneseknek a közös végtelen távoli, ideális pontja. Érdemes a megoldáshoz felhasznált három transzformáció egymás utánját is megvizsgálni: először a szimmetrikus helyzetbe vetítünk, utána tükrözünk a $B\text{'}D\text{'}$ egyenesre, végül visszavetítjük a pontokat és egyeneseket az eredeti síkra. Ez a transzformáció felcseréli az $A$‐$C$, $E$‐$F$, $G$‐$H$, $P$‐$Q$ pontpárokat, és fixen hagyja a $BD$ egyenes pontjait. Az $EF$ és $GH$ egyenesek önmaguk képei, ezért a metszéspontjuk, az $I$ pont is fix. A szorzat transzformációnk a projektív síknak egyfajta tükrözése. Egyenestartó, vagyis egyenesek képe egyenes, van egy tengelye, amelynek minden pontját önmagára képezi, és a tengelyen kívül még egy fixpontja. A sík többi pontjait párosával egymásnak felelteti meg. A projektív transzformációkról, ezek osztályozásáról (és főleg a latin neveikről) sokkal többet lehetne írni, de ez most nem cél.   Körvonal vetítése körvonalra térbeli inverzióval Még adósok vagyunk annak igazolásával, hogy egy körvonalat és egy belső pontját egy másik körvonalba és annak középpontjába lehet vetíteni.   1. lemma. Legyen $k$ körvonal a $\Sigma$ síkban, és $K$ a kör egy belső pontja. Ekkor létezik a térben olyan $\Sigma \text{'}$ sík és olyan, a két síkra nem illeszkedő $O$ pont, hogy $O$-ból vetítve a $k$ kör vetülete a $\Sigma \text{'}$ síkon szintén körvonal, és ennek a körvonalnak a középpontja $K$ vetülete.   Bizonyítás. Húzzuk meg a $k$ körnek a $K$ ponton átmenő egyik átmérőjét, legyen ez $AB$. A $\Sigma$ síkra állítsunk merőleges egyenest a $K$ pontban, és válasszuk ezen az egyik olyan $O$ pontot, amelyre $AOB\sphericalangle$ derékszög. A $K$ pont merőleges vetülete az $OA$ és $OB$ szakaszokon legyen $A\text{'}$, illetve $B\text{'}$. Ezek a pontok mind az $ABO$ háromszög síkjában vannak. Az $OA\text{'}KB\text{'}$ négyszög téglalap, mert az $O$, $A\text{'}$ és $B\text{'}$ csúcsainál is derékszöge van. Legyen $K\text{'}$ a téglalap középpontja; ekkor tehát az $OK$ és $A\text{'}B\text{'}$ szakaszok a $K\text{'}$ pontban felezik egymást (4. ábra). 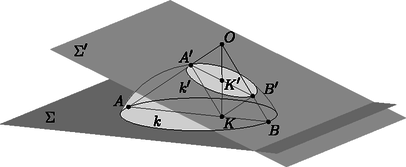    4. ábra   Tekintsük most az $O$ középpontú, $K$-n átmenő gömbre való inverziót; ez a $k$ körvonalat egy $k\text{'}$ körvonalba képezi. Ennek az új körnek a síkja legyen $\Sigma \text{'}$. Az $OAK$ és $OBK$ derékszögű háromszögekben $A\text{'}$, illetve $B\text{'}$ a derékszögű csúcsnak az átfogóra eső vetülete; a befogótétel miatt $OA\cdot OA\text{'}=OB\cdot OB\text{'}=O{K}^2$, tehát az $A$ pont inverzió szerinti képe $A\text{'}$, a $B$ pont képe $B\text{'}$. A $k\text{'}$ kör tehát átmegy az $A\text{'}$ és a $B\text{'}$ ponton. A $k$ kör merőleges az $ABO$ síkra, ezért a $k\text{'}$ is merőleges rá, tehát a $k\text{'}$ körnek az $A\text{'}B\text{'}$ szakasz átmérője, és így a $K\text{'}$ pont a $k\text{'}$ középpontja. Az $O$ pontból vetítve a $\Sigma \text{'}$ síkra, a $k$ kör vetülete a $k\text{'}$ kör, a $K$ pont vetülete pedig $k\text{'}$ középpontja, $K\text{'}$.   Megjegyzés. Nem az imént megszerkesztett $O$ pont (és $\Sigma$-ra való tükörképe) az egyetlen, amely eleget tesz az 1. lemma feltételeinek. Végtelen sok lehetséges vetítési középpont létezik, ezzel kapcsolatban lásd a  485. oldalon a B. 5060. feladatot.   Körök vetítése gömbfelületre A továbbiakban két olyan példa következik, amelyekben egyeneseket és körvonalakat vetítünk a síkból egy gömbfelületre. Ha a síkot invertáljuk egy külső pontból, a sík képe egy gömbfelület, egyedül az inverzió pólusa nem áll elő képként. Ezt a kölcsönösen egyértelmű megfeleltetést sztereografikus projekciónak is hívjuk. A síkbeli egyeneseknek és köröknek a gömbfelületen körvonalak felelnek meg; az egyenesek megfelelői azok a körvonalak, amelyek átmennek az inverzió pólusán. (5. ábra) 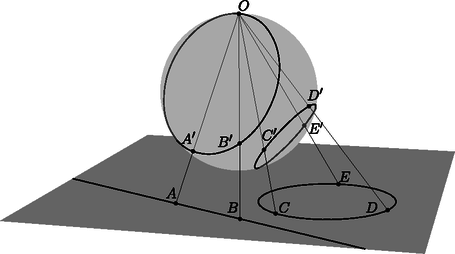    5. ábra   A projektív síkhoz hasonlóan, a síkot kiegészíthetjük egyetlen ideális ponttal, ami az inverzió pólusának felel meg. A sík minden egyenese átmegy ezen az ideális ponton. Az így kapott rendszert hívjuk inverzív síknak. A példáinkban két, közös pont nélküli körvonalat vagy egy kört és egy egyenest fogunk a gömb két párhuzamos körvonalára vetíteni. A következő lemma szerint ez mindig lehetséges.   2. lemma. $a)$ Ha $k$ egy körvonal és $e$ egy egyenes a $\Sigma$ síkban, és nincs közös pontjuk, akkor ezekhez létezik a síkon kívül olyan $O$ pont, hogy $O$-ból invertálva, a $k$ és $e$ képei párhuzamos síkokban fekszenek. $b)$ Ha $k_1$ és $k_2$ két, közös pont nélküli körvonal a $\Sigma$ síkban, akkor ezekhez létezik a síkon kívül olyan $O$ pont, hogy $O$-ból invertálva, a $k_1$ és $k_2$ képei párhuzamos síkokban fekszenek.   Bizonyítás. Mindkét állításhoz hasonló konstrukciót mutatunk, mint az 1. lemma bizonyításában. $a)$ Legyen $AB$ a $k$ kör $e$-re merőleges átmérője, $E$ az $e$ és az $AB$ egyenes metszéspontja. Az $A\mathrm{,}B$ pontokat válasszuk olyan sorrendben, hogy $B$ az $AE$ szakasz belsejében helyezkedjen el. Állítsunk $B$-n keresztül egy $\Sigma$-ra merőleges egyenest, és legyen ezen $O$ olyan pont, amelyre $AOE\sphericalangle ={90}^{\circ }$. A $B$ pont merőleges vetülete az $OA$ és $OE$ szakaszokon legyen $A\text{'}$, illetve $E\text{'}$. Az $OA\text{'}BE\text{'}$ négyszög téglalap (6. ábra). 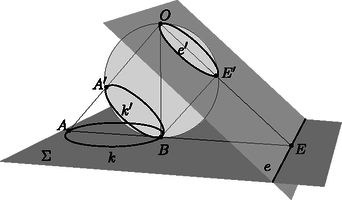    6. ábra   Tekintsük most az $O$ középpontú, $B$-n átmenő gömbre vonatkozó inverziót. Az $A$, $B$, $E$ pontok képe rendre $A\text{'}$, $B\text{'}$, illetve $E\text{'}$, a $\Sigma$ sík képe az $OB$ átmérőjű gömb. A $k$ és $e$ képei az $A\text{'}B$, illetve $OE\text{'}$ egyeneseken keresztül, az $ABO$ síkra állított merőleges síkokban fekszenek, amelyek párhuzamosak egymással. $b)$ Ha a két kör egymáson kívül fekszik, akkor messe a két kör centrálisa a két körvonalat az $A\mathrm{,}B$, illetve $C\mathrm{,}D$ pontokban, ebben a sorrendben. A $\Sigma$ síkra merőlegesen vegyük fel az $AC$ és $BD$ félköröket, ezek metszéspontja legyen $O$. Legyen $O$ merőleges vetülete a síkon $T$, és legyen $T$ merőleges vetülete az $OA$, $OB$, $OC$, $OD$ szakaszokon rendre $A\text{'}$, $B\text{'}$, $C\text{'}$, illetve $D\text{'}$. Az $O$ középpontú, $T$-n átmenő gömbre vonatkozó inverzió a $\Sigma$ síkot az $OT$ átmérőjű gömbre képezi, ezen belül az $A$, $B$, $C$, $D$ pontok képe rendre $A\text{'}$, $B\text{'}$, $C\text{'}$, illetve $D\text{'}$. Mivel $A\text{'}OC\text{'}\sphericalangle =B\text{'}OD\text{'}\sphericalangle ={90}^{\circ }$, a gömbnek $A\text{'}C\text{'}$ és $B\text{'}D\text{'}$ átmérői; emiatt $A\text{'}B\text{'}C\text{'}D\text{'}$ is téglalap. A $k_1$ és $k_2$ körök képei az $A\text{'}B\text{'}$ és $C\text{'}D\text{'}$ átmérőjű, az $ABO$ síkra merőleges körök, amelyek tehát egyenlő sugarúak, és egymással párhuzamos síkokban vannak (7. ábra). 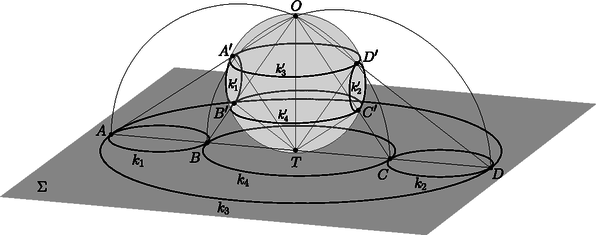    7. ábra   Ha $k_1$ és $k_2$ nem egymáson kívül helyezkedik el, akkor az ábrán a $k_3$ és $k_4$ körökkel mondhatjuk el ugyanezt.   Megjegyzés. Vegyük észre, hogy mindkét esetben az $ABO$ sík merőleges volt a $\Sigma$ síkra. Az $a)$ részben az $OE$ egyenes merőleges $e$-re. Be lehet bizonyítani, hogy csak ilyen tulajdonságú $O$ pontok teljesíthetik a lemma feltételeit.   3. példa. Legyen az $ABC$ háromszög körülírt köre $\omega$, és $\ell$ egy egyenes, amelynek nincs közös pontja $\omega$-val. Jelöljük $P$-vel $\omega$ középpontjának merőleges vetületét $\ell$-en. A $BC$, $CA$, $AB$ oldalegyenesek $\ell$-et rendre a $P$-től különböző $X$, $Y$, illetve $Z$ pontokban metszik. Bizonyítsuk be, hogy az $AXP$, $BYP$ és $CZP$ háromszögek köré írt köröknek vagy van még egy, $P$-től különböző közös pontja, vagy pedig $P$-ben érintik egymást (8. ábra). (IMO Shortlist 2012/G8; Cosmin Pohoata feladata) 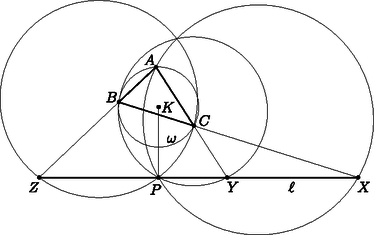      8. ábra     Megoldás. Invertáljuk az ábrát a 2. lemma $a)$ része szerint egy alkalmas $O$ pontból úgy, hogy az $\omega$ kör és az $\ell$ egyenes képei párhuzamos síkokban fekvő körök legyenek. Az egyes objektumok képét most is vesszővel fogjuk jelölni. Az ábra síkjának képe egy $\text{G}$ gömb; ennek felszínén helyezkedik el az $\omega \text{'}$ kör, ami átmegy az $A\text{'}$, $B\text{'}$ és $C\text{'}$ pontokon, továbbá az $\ell \text{'}$ kör, amely átmegy az $X\text{'}$, $Y\text{'}$, $Z\text{'}$ és $P\text{'}$ pontokon és az inverzió pólusán, az $O$ ponton. A 2. lemma konstrukciójában $OP$ merőleges $\ell$-re, ezért az $OP\text{'}$ szakasz az $\ell \text{'}$ körnek átmérője. A Thalész-tétel miatt tehát 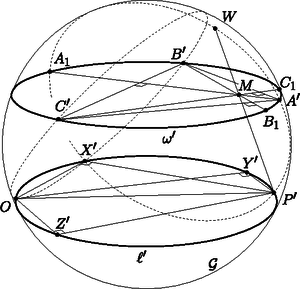$OX\text{'}P\text{'}\sphericalangle =OY\text{'}P\text{'}\sphericalangle =OZ\text{'}P\text{'}\sphericalangle ={90}^{\circ }$ (9. ábra).       9. ábra     Az $BCX$ egyenes inverzió szerinti képe egy $O$-t átmenő körvonal, ezért a $B\text{'}$, $C\text{'}$, $X\text{'}$, $O$ pontok egy körvonalon vannak. Ennek a körnek a síkja az $\omega \text{'}$ és $\ell \text{'}$ körök egymással párhuzamos síkjait párhuzamos egyenesekben metszi, vagyis a $B\text{'}C\text{'}$ szakasz párhuzamos $OX\text{'}$-vel. Legyen $A_1$ az $\omega \text{'}$ kör és az $A\text{'}P\text{'}X\text{'}$ kör második, $A\text{'}$-től különböző metszéspontja. Az $A\text{'}P\text{'}X\text{'}$ sík szintén két párhuzamos egyenesben metszi az $\omega \text{'}$ és $\ell \text{'}$ körök síkjait, ezért $A\text{'}{A}_1$ párhuzamos $P\text{'}X\text{'}$-vel. Mivel az $OX\text{'}$ és $P\text{'}X\text{'}$ szakaszok merőlegesek, a velük párhuzamos $B\text{'}C\text{'}$ és $A\text{'}{A}_1$ szakaszok merőlegesek egymásra. Tehát az $A\text{'}B\text{'}C\text{'}$ háromszögben $A\text{'}{A}_1$ a $BC$ oldalhoz tartozó magasságvonal. Hasonlóan, legyen $B_1$ és $C_1$ a $\omega \text{'}$ kör második metszéspontja a $B\text{'}P\text{'}Y\text{'}$ és $C\text{'}P\text{'}Z\text{'}$ körökkel; ekkor $B\text{'}{B}_1$ és $C\text{'}{C}_1$ az $A\text{'}B\text{'}C\text{'}$ háromszög másik két magassága. Legyen ezután $M$ az $A\text{'}B\text{'}C\text{'}$ háromszög magasságpontja, és legyen $W$ a $P\text{'}M$ egyenes másik, $P\text{'}$-től különböző metszéspontja a $\text{G}$ gömbbel. Az $A\text{'}$, $P\text{'}$, $X\text{'}$ és $W$ pontok az egymással párhuzamos $A\text{'}{A}_1$ és $P\text{'}X\text{'}$ szakaszok síkjában, tehát egy körvonalon vannak. Visszainvertálva a síkra azt kapjuk, hogy $W$ képe, $W\text{'}$ rajta van az $AXP$ körön. Ugyanígy láthatjuk, hogy a $BYP$ és a $CZP$ kör is átmegy a $W\text{'}$ ponton. Ha a $W$ pont nem jön létre, mert az $P\text{'}M$ egyenes érinti a gömböt, akkor az $PM\text{'}$ egyenes közös érintője az $A\text{'}X\text{'}P\text{'}$, $B\text{'}Y\text{'}P\text{'}$ és $C\text{'}Z\text{'}P\text{'}$ köröknek, ezért a síkbeli $AXP$, $BYP$ és $CZP$ körök is érintik egymást a $P$ pontban.   4. példa. Adottak a síkon a $k_0$, $k_1$, $k_2$, $k_3$ és $k_4$ körök úgy, hogy $i=\mathrm{1,2,3,4}$ esetén $k_i$ kívülről érinti $k_0$-t a $T_i$ pontban, továbbá $k_i$ kívülről érinti $k_{i+1}$-et az $S_i$ pontban ($k_5=k_1$). Legyen $O$ a $k_0$ középpontja, $T$ a $T_1{T}_3$ és $T_2{T}_4$ egyenesek metszéspontja, és legyen $S$ az $S_1{S}_3$ és $S_2{S}_4$ egyenesek metszéspontja. Igazoljuk, hogy $O$, $T$ és $S$ egy egyenesen van. (KöMaL A. 597., 2013. október; Mester Márton feladata)   Megoldás. Először megmutatjuk, hogy az $S_1$, $S_2$, $S_3$, $S_4$ pontok egy körön vannak. 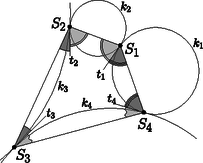      10. ábra     Jelöljük $t_i$-vel a $k_1$ és $k_{i+1}$ közös belső érintőjét. Az $S_i{S}_{i+1}$ húrok ugyanakkora szöget zárnak be a $t_i$ és $t_{i-1}$ érintőkkel. Ebből láthatjuk, hogy az $S_1{S}_2{S}_3{S}_4$ négyszög szemközti szögeinek összege egyenlő, $S_1{S}_2{S}_3{S}_4$ húrnégyszög (10. ábra). Jelöljük a körülírt körét $u$-val, $u$ középpontját $U$-val. Az $u$ kör $S_i{S}_{i+1}$ íve a $k_{i+1}$ kör belsejében fekszik, így a $k_1$, $k_2$, $k_3$, $k_4$ körök lefedik $u$-t, míg ugyanezek a körök kívülről érintik $k_0$-t. Ezért a $k_0$ és $u$ köröknek nincs közös pontja. A 2. lemma $b)$ része szerint létezik olyan térbeli inverzió, ami a $k_0$ és $u$ köröket párhuzamos síkú körökbe viszi. Tekintsünk egy ilyen inverziót; a pólusa legyen $X$, az egyes objektumok képét most is vesszővel fogjuk jelölni. (11. ábra). A sík képe egy gömbfelület, a körök és egyenesek képe egy-egy, a gömbre illeszkedő kör; egymást érintő görbék képei egymást érintő görbék. 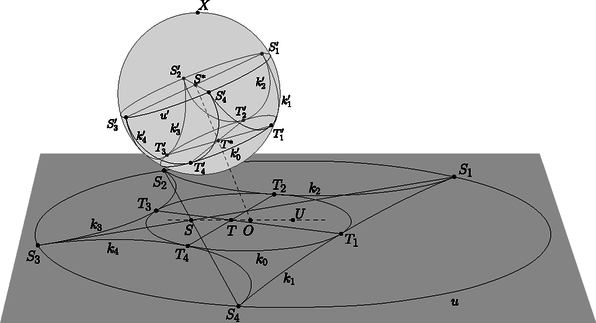    11. ábra   Minden egyes $i$-re a $k_i\text{'}$ és $u\text{'}$ körök szöge, valamint a $k_{i+1}\text{'}$ és $u\text{'}$ körök szöge ${180}^{\circ }$-ra egészíti ki egymást. Ebből következik, hogy $k_1\text{'}$ és $k_3\text{'}$, illetve $k_2\text{'}$ és $k_4\text{'}$ ugyanakkora, $S_1\text{'}{S}_2\text{'}{S}_3\text{'}{S}_4\text{'}$ téglalap, $T_1\text{'}{T}_2\text{'}{T}_3\text{'}{T}_4\text{'}$ pedig négyzet. Legyen $S^{*}=S_1\text{'}{S}_3\text{'}\cap S_3\text{'}{S}_4\text{'}$ és $T^{*}=T_1\text{'}{T}_3\text{'}\cap T_3\text{'}{T}_4\text{'}$ az $u\text{'}$, illetve a $k_0\text{'}$ kör középpontja. Mivel $X$, $T_i$ és $T_i\text{'}$ egy egyenesre esik, az $X$, $T_i$, $T_{i+2}$, $T_i\text{'}$, $T_{i+2}\text{'}$ pontok egy síkra esnek ($i=\mathrm{1,2}$). E két sík metszésvonala $X{T}^{*}T$. Hasonlóan, $X$, $S^{*}$, $S$ egy egyenesen van. Az $X{S}^{*}{T}^{*}$ síkra a $k_0\text{'}$ és az $u\text{'}$ kör is szimmetrikus, ezért az inverzeik is; ezért középpontjaik, $O$, illetve $U$ a $X{S}^{*}{T}^{*}$ síkban van. Az $O$, $U$, $S$, $T$ pontok mindegyike az eredeti sík és az $X{S}^{*}{T}^{*}$ sík közös részén helyezkedik el, ez a négy pont tehát egy egyenesen van.   Függelék: Az inverzió alaptulajdonságai Az inverzió egy geometriai transzformáció, síkban és térben is értelmezzük. Síkban a tengelyes, térben a síkra való tükrözéshez hasonlít, de a tengely helyett síkban egy körvonalra, térben egy gömbfelületre ,,tükrözünk''. A síkbeli inverzió definíciójához vegyünk fel egy $O$ középpontú, $r$ sugarú $k$ kört; az $O$ pont az inverzió középpontja vagy pólusa; a $k$ lesz az inverzió alapköre. Bármely, $O$-tól különböző $P$ pontra legyen $P\text{'}$ az $OP$ félegyenesnek az a pontja, amelyre $OP\cdot OP\text{'}=r^2$; ez a $P\text{'}$ a $P$ pont $k$-ra vonatkozó inverze vagy tükörképe. Az inverzió a sík $O$-tól különböző pontjait rendeli egymáshoz. Az világos, hogy $P\text{'}$ inverze a $P$ pont, és az alapkör pontjai önmaguk inverzei. Ezért is tekinthetjük a $k$ kört egyfajta szimmetriatengelynek. Bizonyítás nélkül felsoroljuk az inverzió néhány legfontosabb tulajdonságát. Ezek bizonyítása jó gyakorló feladat; hasonló háromszögekkel és az $O$ pont különböző körökre vonatkozó hatványaival nem nehezek. $•$ Az $O$-n átmenő egyenesek képei (eltekintve az $O$ ponttól) önmaguk. $•$ Ha egy egyenes nem megy át $O$-n, akkor az inverze egy $O$-n átmenő körvonal, és fordítva: az $O$-n átmenő körök képei $O$-ra nem illeszkedő egyenesek. $•$ Az $O$-t nem tartalmazó körvonalak képei $O$-t nem tartalmazó körvonalak. $•$ Az alapkört merőlegesen metsző körvonalak önmaguk képei. $•$ Az inverzió érintés-, merőleges- és általában szögtartó: ha $a$ és $b$ két egyenes vagy kör, amelyek az $O$-tól különböző $P$ pontban $\alpha$ szögben metszik egymást, akkor képeik, $a\text{'}$ és $b\text{'}$ a $P\text{'}$ pontban szintén $\alpha$ szögben metszik egymást. $•$ Az inverzió kettősviszonytartó: ha $A$, $B$, $C$, $D$ négy pont egy egyenesen vagy körön, akkor $\left(A\mathrm{,}B\mathrm{,}C\mathrm{,}D\right)=\left(A\text{'}\mathrm{,}B\text{'}\mathrm{,}C\text{'}\mathrm{,}D\text{'}\right)$. $•$ Az inverzió szimmetriatartó: ha $t$ egyenes vagy kör, $P$ és $Q$ egymás tükörképe $t$-re, akkor képeik, $P\text{'}$ és $Q\text{'}$ is egymás tükörképei $t\text{'}$-re. A térbeli inverzió definíciója lényegében ugyanaz, csak kör helyett egy $O$ középpontú, $r$ sugarú gömbre invertálunk. Az $O$-n átmenő síkokon belül a fenti tulajdonságok érvényben maradnak. $•$ Az $O$-n átmenő egyenesek és síkok képei (eltekintve az $O$ ponttól) önmaguk. $•$ Ha egy egyenes nem megy át $O$-n, akkor az inverze ugyanabban a síkban egy $O$-n átmenő körvonal, és fordítva: az $O$-n átmenő körvonalak képei $O$-ra nem illeszkedő egyenesek. $•$ Ha egy sík nem megy át $O$-n, akkor az inverze egy $O$-n átmenő gömbfelület, és fordítva: az $O$-n átmenő gömbfelületek képei $O$-ra nem illeszkedő síkok. $•$ Az $O$-t nem tartalmazó gömbfelületek képei $O$-t nem tartalmazó gömbfelületek. $•$ Az alapgömböt merőlegesen metsző gömbfelületek önmaguk képei. $•$ Az egyenesek és körvonalak inverzei is egyenesek vagy körvonalak. $•$ Az inverzió térben is szögtartó: ha $a$ és $b$ két egyenes, kör, sík vagy gömbfelület, amelyeknek van legalább egy, $O$-tól különböző pontjuk, és $\alpha$ szögben metszik egymást, akkor képeik, $a\text{'}$ és $b\text{'}$ szintén $\alpha$ szögben metszik egymást. $•$ Az inverzió szimmetriatartó: ha $\text{S}$ sík vagy gömbfelület, $P$ és $Q$ egymás tükörképe $\text{S}$-re, akkor képeik, $P\text{'}$ és $Q\text{'}$ is egymás tükörképei $\text{S}\text{'}$-re.   A síkban és a térben is, a definícióban az $r^2$ helyére negatív számot is írhatunk. Az így módosított definícióban $P\text{'}$ az $OP$ egyenesnek az a pontja, amelyre $\overrightarrow{OP}\cdot \overrightarrow{OP\text{'}}=\lambda$; ha a $\lambda$ paraméter pozitív, akkor $P\text{'}$ és $P$ az $O$-nak ugyanazon az oldalán, negatív $\lambda$ esetén ellentétes oldalon vannak.   További olvasnivaló Projektív transzformációkról és inverzióról ismét csak Reiman István Geometria és határterületei c. könyvét tudom ajánlani. A bemutatott példákra sokféle más megoldás is létezik; néhányat megtaláltok ezeken a címeken: https://www.komal.hu/feladat?a=feladat&f=A594 https://www.komal.hu/feladat?a=feladat&f=A597 https://www.imo-official.org/problems/IMO2012SL.pdf, 38‐41. oldal.   Feladatok   1. $a)$ Igazoljuk az 1. példa állítását csupán a kerületi szögek tételének felhasználásával. Legyen az $EG$ és $FH$ szakaszok metszéspontja $K$, a beírt kör középpontja $I$, és $I$ merőleges vetülete az $AC$ átlón $T$. Mutassuk meg, hogy az $E\mathrm{,}F\mathrm{,}K\mathrm{,}T$, valamint a $G\mathrm{,}H\mathrm{,}K\mathrm{,}T$ pontok is egy-egy körön vannak, és az $AC$ átló átmegy a $K$ ponton. $b)$ Igazoljuk az 1. példa állítását úgy, hogy felírjuk a Brianchon-tételt az $AEBCGD$ és $ABFCDH$ elfajuló érintőhatszögekre. $c)$ Igazoljuk az 1. példa állítását úgy, hogy felírjuk a Pascal-tételt az $EEGFFH$,$$$$ $EGGFHH$, $EEFHHG$ és $EFFHGG$ elfajuló húrhatszögekre.   2. Az $ABCD$ érintőnégyszögben legyen $PQ$ a beírt kör $AC$-re merőleges átmérője. Tegyük fel, hogy a $BP$ és $DQ$ egyenesek az $X$, a $BQ$ és $DP$ egyenesek az $Y$ pontban metszik egymást. Mutassuk meg, hogy az $X$ és $Y$ pontok az $AC$ egyenesen vannak. (International Olympiad of Metropolises, Moszkva, 2018/2)   3. Adott egy $k$ kör és rajta kívül két pont, $A$ és $B$. Az $A$-ból $k$-hoz húzott érintő szakaszok $A{C}_1$ és $A{C}_2$, a $B$-ből $k$-hoz húzott érintő szakaszok $B{D}_1$ és $B{D}_2$. Igazoljuk, hogy a $C_1{C}_2$ egyenes akkor és csak akkor megy át a $B$ ponton, ha a $D_1{D}_2$ egyenes átmegy az $A$ ponton. (Avagy, $A$ polárisa akkor és csak akkor megy át $B$-n, ha $B$ polárisa átmegy $A$-n.)   4. Igazoljuk, hogy ha két, egy síkban fekvő körnek nincs közös pontja, akkor van olyan inverzió, amely ezeket a köröket koncentrikus körökbe képezi.   5. Adott a térben két körvonal, $k_1$ és $k_2$ úgy, hogy a síkjaik metszik egymást. Mutassuk meg, hogy ha a két kört egymásra lehet vetíteni egy alkalmas $O$ pontból, akkor a két körvonal egymás inverze egy $O$ középpontú inverzió szerint.