Cím:	Megoldásvázlatok a 2019/6. szám emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Fridrik Richárd
Füzet:	2019/október, 402 - 412. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Dani kerékpárversenyre készül. Először hegynek felfelé, utána vízszintes terepen, majd lejtőn lefelé hajtja a biciklit, ezután visszafelé ugyanezen az útvonalon hajt végig. Lejtőn lefelé $60\frac{\text{km}}{\text{h}}$, vízszintes terepen $40\frac{\text{km}}{\text{h}}$, míg hegynek felfelé $20\frac{\text{km}}{\text{h}}$ állandó sebességgel képes haladni. Az odafele utat 1,75 óra alatt, míg a visszafele utat 2,25 óra alatt tette meg. Milyen hosszúak az egyes útszakaszok, ha oda-vissza összesen 130 km-t biciklizett? (Közben sehol sem állt meg, a visszafordulás időveszteség nélkül zajlódik le.)   (13 pont)   Megoldás. Jelöljük az egymás után következő utak hosszát (km-ben megadva) rendre $a$; $b$; $c$-vel. Dani az odafelé és a visszafelé vezető úton is először hegynek felfelé, majd vízszintes úton, végezetül lejtőn lefelé halad. Az odafelé vezető úton $a$, míg a visszafelé vezető úton $c$ km hosszú úton halad hegynek felfelé. Az előbbieket és a $t=\frac{s}{v}$ összefüggést felhasználva kapjuk a következő egyenletrendszert: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle \frac{a}{20}+\frac{b}{40}+\frac{c}{60}}& {\displaystyle =1\mathrm{,}\mathrm{75,}}\hfill & \text{(<mi>I</mi>)}\\ \hfill {\displaystyle \frac{c}{20}+\frac{b}{40}+\frac{a}{60}}& {\displaystyle =2\mathrm{,}\mathrm{25,}}\hfill & \text{(<mi>I</mi><mi>I</mi>)}\\ \hfill {\displaystyle 2\cdot \left(a+b+c\right)}& {\displaystyle =\mathrm{130,}}\hfill & \text{(<mi>I</mi><mi>I</mi><mi>I</mi>)}\end{array}}$ azaz ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle 6a+3b+2c}& {\displaystyle =\mathrm{210,}}\hfill & \text{(<mi>I</mi>)}\\ \hfill {\displaystyle 2a+3b+6c}& {\displaystyle =\mathrm{270,}}\hfill & \text{(<mi>I</mi><mi>I</mi>)}\\ \hfill {\displaystyle a+b+c}& {\displaystyle =65.}\hfill & \text{(<mi>I</mi><mi>I</mi><mi>I</mi>)}\end{array}}$ Fejezzük ki a III. egyenletből $c$-t és helyettesítsük be a másik két egyenletbe. Mivel $c=65-a-b$, ezért ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle 4a+b}& {\displaystyle =\mathrm{80,}}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle 4a+3b}& {\displaystyle =120}\hfill & \text{(<mn>2</mn>)}\end{array}}$ adódik. Ezt megoldva kapjuk, hogy az egyes útszakaszok $a=15$; $b=20$; $c=30$ km hosszúak. Ellenőrzés a feladat szövege alapján.   2. Tekintsük a következő állításokat. $A$: Meg tudunk úgy adni végtelen sok prímet, hogy bármely kettő összege ne legyen prím. $B$: Ha az $a_n^2$ sorozat konvergens, akkor $a_n$ is konvergens. $C$: Ha öt különböző természetes szám összege osztható öttel, akkor öttel osztva különböző maradékot adnak. $a)$ Döntsük el, hogy igazak vagy hamisak az állítások. Válaszainkat indokoljuk.   (8 pont) $b)$ Fogalmazzuk meg a $C$ állítás megfordítását. Döntsük el, hogy igaz vagy hamis az állítás megfordítása. Válaszunkat indokoljuk.  (4 pont)   Megoldás. $a)$ Az $A$ állítás igaz, hiszen ha vesszük a páratlan prímeket, azok kielégítik a feltételeket. Nyilván végtelen sok van belőlük, mert végtelen sok prímszám van és az egyedüli páros prím a 2. Másrészt bármely két páratlan prím összege 2-nél nagyobb páros szám, ami biztosan nem prím. A $B$ állítás hamis, pl. $a_n={\left(-1\right)}^n$ esetén $a_n^2=1$, ami nyilván konvergens, de az $a_n={\left(-1\right)}^n$ sorozatról tudjuk, hogy nem konvergens. A $C$ állítás hamis, pl. 5; 10; 15; 20; 25 különböző számok összege osztható öttel, de öttel osztva nem adnak különböző maradékot (sőt, azonos maradékot adnak). $b)$ A $C$ állítás megfordítása: Ha öt különböző természetes szám öttel osztva különböző maradékot ad, akkor összegük osztható öttel. Ez igaz, hiszen egy szám ötös maradéka 0; 1; 2; 3; 4 lehet, de a feltételek szerint ezek mindegyike fel is lép, méghozzá pontosan egyszer. A maradékok összege 10, ami osztható öttel. Az állítás megfordítása igaz.   3. $a)$ Döntsük el, hogy az implikáció asszociatív művelet-e, azaz tetszőleges $A$; $B$; $C$ kijelentések esetén fennáll-e, hogy $\left(A\to B\right)\to C=A\to \left(B\to C\right)$.  (4 pont) $b)$ Határozzuk meg azon $P\left(x;y\right)$ pontok halmazát a derékszögű koordinátarendszerben, amelyek koordinátáira igaz, hogy ${PA}^2+{PB}^2=22$, ahol $A\left(1;2\right)$ és $B\left(3;0\right)$.   (8 pont)   Megoldás. $a)$ Írjuk fel az igazságtáblázatot. Mivel van olyan kiértékelés, amelynél a két állítás logikai értéke nem egyezik meg, ezért a két állítás nem egyezik meg, azaz az implikáció nem asszociatív művelet.   ${\displaystyle \begin{array}{|ccccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mo stretchy="true">→</mo><mi>B</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi><mo stretchy="true">→</mo><mi>C</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>A</mi><mo stretchy="true">→</mo><mi>B</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="true">→</mo><mi>C</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mo stretchy="true">→</mo><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>B</mi><mo stretchy="true">→</mo><mi>C</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math> }}\hfill \\ \hfill {\displaystyle \text{i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i }}\hfill \\ \hfill {\displaystyle \text{i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h }}\hfill \\ \hfill {\displaystyle \text{i}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i }}\hfill \\ \hfill {\displaystyle \text{h}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i }}\hfill \\ \hfill {\displaystyle \text{i}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i }}\hfill \\ \hfill {\displaystyle \text{h}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ i }}\hfill \\ \hfill {\displaystyle \text{h}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i }}\hfill \\ \hfill {\displaystyle \text{h}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ i }}\hfill \\ \hline\end{array}}$   $b)$ Írjuk fel a két pont távolságára vonatkozó összefüggést: $\begin{array}{c}{\displaystyle PA=\sqrt[]{{\left(x-1\right)}^2+{\left(y-2\right)}^2}\text{és}PB=\sqrt[]{{\left(x-3\right)}^2+{\left(y-0\right)}^2}\mathrm{.}}\end{array}$ Mivel ${PA}^2+{PB}^2=22$, ezért ${\left(x-1\right)}^2+{\left(y-2\right)}^2+{\left(x-3\right)}^2+y^2=22$. Ezt kibontva és rendezve azt kapjuk, hogy $2x^2+2y^2-8x-4y-8=0$. Egyszerűsítve 2-vel és teljes négyzeteket kialakítva kapjuk, hogy ${\left(x-2\right)}^2+{\left(y-1\right)}^2=9$. Tehát a keresett pontok mértani helye egy kör, melynek középpontja $K\left(2;1\right)$ és sugara $r=3$. Könnyen látszik, hogy a körvonal minden pontja kielégíti a feladat feltételeit.   4. Legyen $A$ a $2^x+2^{1-x}\le 3$ egyenlőtlenség megoldáshalmaza, $B$ pedig az alábbi két függvény értékkészletének közös része: $\begin{array}{c}{\displaystyle f\left(x\right)=\frac{2}{3}\cdot \text{sin}\left(2019\pi x\right)\text{és}g\left(x\right)={4x}^2-4x+\frac{3}{2}\mathrm{.}}\end{array}$ $a)$ Határozzuk meg az $A$ halmazt.  (5 pont) $b)$ Határozzuk meg a megadott függvények értékkészletét és a $B$ halmazt.   (7 pont) $c)$ Hány eleme van az $\left(A\setminus B\right)\cap \text{Z}$ halmaznak, ahol $\text{Z}$ az egész számok halmazát jelöli?  (2 pont)   Megoldás. $a)$ $2^x+2^{1-x}\le 3\leftrightarrow 2^x+\frac{2}{2^x}\le 3$. Mindkét oldalt szorozzuk meg a $2^x>0$ kifejezéssel és rendezzük az egyenlőtlenséget. Ekkor az egyenlőtlenség iránya nem változik meg, hiszen pozitív kifejezéssel szoroztunk. ${\left(2^x\right)}^2-3\cdot 2^x+2\le \mathrm{0,}$ vezessük be az $a=2^x>0$ ismeretlent. Az $a^2-3a+2\le 0$ egyenlőtlenség megoldása: $1\le a\le 2$. Most írjuk vissza $a=2^x$-t. Az $f\left(x\right)=2^x$ függvény szigorúan monoton nő, ezért az $1\le 2^x\le 2$ egyenlőtlenség megoldása: $x\in \left[0;1\right]$. Tehát $A=\left[0;1\right]$. $b)$ Mivel $\forall t\in \text{R}$ esetén $-1\le \text{sin}t\le 1$, ezért $-1\le \text{sin}\left(2019\pi x\right)\le 1$, így az $f$ függvény értékkészlete: $R_f=[-\frac{2}{3};\frac{2}{3}]$. A $g$ függvényt teljes négyzetté alakítjuk: $\begin{array}{c}{\displaystyle g\left(x\right)=4x^2-4x+\frac{3}{2}=4\cdot {\left(x-\frac{1}{2}\right)}^2+\frac{1}{2}\mathrm{,}}\end{array}$ így $R_g=[\frac{1}{2};\infty [$. Innen $R_f\cap R_g=[\frac{1}{2};\frac{2}{3}]$. Tehát $B=[\frac{1}{2};\frac{2}{3}]$. $c)$ Látható, hogy $A\setminus B=[0;\frac{1}{2}[\cup ]\frac{2}{3};1]$. Innen kapjuk, hogy $\left(A\setminus B\right)\cap \text{Z}=\left\{0;1\right\}$, ennek a halmaznak pedig két eleme van.   II. rész     5. $a)$ Egyik este Anna, Bea, Csilla, Dóra és Emese elmentek vacsorázni a közeli pizzázóba. Mindannyian másféle pizzát rendeltek. A pincér még új, így a rendelt ételeket véletlenszerűen osztotta ki a lányoknak (de azokat hozta ki, amiket rendeltek). Jelölje $X$ azt a valószínűségi változót, amely azt adja meg, hogy hányan kapták a saját rendelésüket. Határozzuk meg $X$ várható értékét.  (8 pont) $b)$ Oldjuk meg az alábbi egyenletet a pozitív egész számok halmazán: $\begin{array}{c}{\displaystyle 2^n-1=m^2\mathrm{.}}\end{array}$ (8 pont)   Megoldás. $a)$ Könnyen látható, hogy $X$ értékkészlete a $\left\{0;1;2;3;5\right\}$ halmaz. Ezek valóban megvalósíthatók. Az $X$ nyilván nem veheti fel a 4 értéket, mert ha 4 pizzát a megfelelő személy kap, akkor az ötödiket is csak az azt megrendelő személy kaphatja. A pincér összesen $5!=120$ különböző módon oszthatja ki a pizzákat, így $P\left(X=5\right)=\frac{1}{120}$. $P\left(X=3\right)=\frac{\left(\genfrac{}{}{0ex}{}{5}{3}\right)}{120}=\frac{10}{120}$, mivel ki kell választani azt a 3 főt, akik jó pizzát kapnak és a másik 2 ember csak egyféleképpen nem kaphatja a sajátját. $P\left(X=2\right)=\frac{\left(\genfrac{}{}{0ex}{}{5}{2}\right)\cdot 2}{120}=\frac{20}{120}$, mivel ki kell választani azt a 2 főt, akik jó pizzát kapnak és a másik 3 embernél kétféleképpen történhet meg az, hogy senki sem kapja a saját rendelését. Ugyanis jelöljük pl. $A$; $B$; $C$-vel azokat az embereket, akik az $a$; $b$; $c$ pizzákat rendelték és egyikük sem kapta a sajátját. Ennek lehetőségei:   ${\displaystyle \begin{array}{|ccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>b</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math> }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi></math> }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>b</mi></math> }}\hfill \\ \hline\end{array}}$ $P\left(X=1\right)=\frac{\left(\genfrac{}{}{0ex}{}{5}{1}\right)\cdot 9}{120}=\frac{45}{120}$. Itt egyedül a 9-et érdemes magyarázni az alábbi táblázattal:   ${\displaystyle \begin{array}{|cccccccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>b</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>b</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>b</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>d</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>d</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>d</mi></math> }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>d</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>d</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>d</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math> }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>d</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>d</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>d</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>b</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>b</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>b</mi></math> }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>b</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>b</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>b</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi></math> }}\hfill \\ \hline\end{array}}$   A várható érték kiszámolásához $P\left(X=0\right)$ értékére nincs szükségünk, ugyanis ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle E\left(X\right)}& {\displaystyle =}\hfill & {\displaystyle 0\cdot P\left(X=0\right)+1\cdot P\left(X=1\right)+2\cdot P\left(X=2\right)+3\cdot P\left(X=3\right)+}\hfill \\ \hfill {\displaystyle }& {\displaystyle }\hfill & {\displaystyle +5\cdot P\left(X=5\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =}\hfill & {\displaystyle 0+1\cdot \frac{45}{120}+2\cdot \frac{20}{120}+3\cdot \frac{10}{120}+5\cdot \frac{1}{120}=1.}\hfill \end{array}}$   Megjegyzések. $P\left(X=0\right)$ értéke többféle módon is meghatározható. 1. Tudjuk, hogy $P\left(X=0\right)+P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=5\right)=1$, hiszen ezek eloszlást alkotnak. Innen $P\left(X=0\right)=\frac{44}{120}$ adódik. 2. Lényegében azt kell meghatározni $P\left(X=0\right)$ esetén, hogy mennyi a kedvező esetek száma. Ezen esetek száma valójában azt adja meg, hogy öt elemnek hány olyan permutációja van, amikor semelyik sem kerül a helyére, ún. fixpontmentes. Ismert az alábbi összefüggés $n$ elem fixpontmentes permutációinak számára: $\begin{array}{c}{\displaystyle n!\cdot \left(\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}-\text{...}+\frac{{\left(-1\right)}^n}{n!}\right)\mathrm{.}}\end{array}$ Itt $n$ helyére 5-öt helyettesítve éppen 44-et kapunk eredményül. 3. A 44-et másképpen is megkaphatjuk. Gondoljuk meg, hogy pl. Anna $a$ pizzája hány helyre kerülhet: 4 helyre. Kerüljön pl. Beához. Ezen belül vizsgálunk két lényegesen eltérő esetet aszerint, hogy Bea $b$ pizzája hová kerül. $i)$ Ha Bea $b$ pizzája Annához kerül. Ekkor lényegében arról van szó, hogy Anna kapta Bea pizzáját és viszont. Így azt kell megválaszolni, hogy hány olyan eset van, amikor Csilla, Dóra és Emese egyike sem kapja a saját pizzáját. Ebből 2 eset van, ezt már láttuk. Ekkor összesen $4\cdot 2=8$ jó esetünk van. $ii)$ Ha Bea $b$ pizzája nem Annához kerül. Ekkor 4 embernek kell kiosztani 4 pizzát úgy, hogy mindegyiknél pontosan 1 pizza van tiltva, hogy odakerüljön. Ezen eseteket is megszámoltuk már, ezekből 9 eset van. Ekkor összesen $4\cdot 9=36$ jó esetünk van. Tehát összesen $8+36=44$ jó eset van. 4. Ha $d_n$-nel jelöljük a fixpontmentes permutációk számát $n$ elem esetén, akkor teljesül az alábbi rekurzió: $d_1=0$; $d_2=1$; $d_n=\left(n-1\right)\cdot d_{n-1}+\left(n-1\right)\cdot d_{n-2}$, $n\ge 3$ esetén. $b)$ Mivel $n\in {\text{N}}^{+}$, ezért $2^n-1$ páratlan, így $m^2$ is páratlan, tehát $m$ páratlan. Legyen $m=2k+1$, ahol $k\in \text{N}$. Egyenletünk az alábbi alakot ölti: $2^n-1={\left(2k+1\right)}^2$, ahonnan $2^n=4k^2+4k+2$. A jobb oldali kifejezés 4-gyel osztva (sőt 8-cal osztva is) 2 maradékot ad. Ha $n\ge 2$, akkor $4\mid 2^n$. Ekkor nem kapunk megoldást. Tehát, ha van megoldás, az csak akkor lehet, ha $n=1$. Ha $n=1$, akkor $m=1$. Ez valóban megoldása az egyenletnek.   6. $a)$ Egy derékszögű háromszög beírt és köré írt körének sugarát jelölje $r$ és $R$. Mekkorák a háromszög oldalai, ha tudjuk, hogy $r+R=31$ és $rR=150?$  (8 pont) $b)$ Egy szabályos ötszög mindegyik oldalát kiszínezzük három adott szín valamelyikével. Hányféleképpen tehetjük ezt meg, ha két színezést nem tekintünk különbözőnek, ha forgatással egymásba vihetők?  (8 pont)   Megoldás. $a)$ Megoldjuk az ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle r+R}& {\displaystyle =\mathrm{31,}}\hfill & \text{(<mi>I</mi>)}\\ \hfill {\displaystyle rR}& {\displaystyle =150}\hfill & \text{(<mi>I</mi><mi>I</mi>)}\end{array}}$ egyenletrendszert. Mivel $R=31-r$, ezért $r\left(31-r\right)=150$, innen $r_1=25$; $r_2=6$ és $R_1=6$; $R_2=25$ adódik. Derékszögű háromszögben teljesül, hogy $r=\frac{a+b-c}{2}$ és $R=\frac{c}{2}$. A továbbiakban két esetet vizsgálunk meg. 1. eset: Ha $r=25$ és $R=6$. Érezhető, hogy ekkor nem fogunk megoldást kapni, de ezt igazoljuk is. $\frac{a+b-c}{2}=25$ és $\frac{c}{2}=6$, így $c=12;a+b=62$. Pitagorasz tétele szerint $a^2+b^2=c^2=144$, így mivel $b=62-a$, az alábbi másodfokú egyenletet kapjuk, melynek nincs valós megoldása: $a^2-62a+1850=0$. 2. eset: Ha $r=6$ és $R=25$. Ekkor $\frac{a+b-c}{2}=6$ és $\frac{c}{2}=25$, így $c=50$; $a+b=62$. Pitagorasz tétele szerint $a^2+b^2=c^2=2500$, továbbá $b=62-a$. Az alábbi másodfokú egyenletet kapjuk: $a^2-62a+672=0$. Így $a_1=14$; $a_2=48$ adódik, melyekre a $b_1=48$; $b_2=14$ értékeket kapjuk. Tehát a háromszög oldalai: 14; 48; 50, melyek valóban kielégítik a feladat feltételeit. $b)$ Legyen a három szín pl. piros, kék és zöld. Aszerint fogunk eseteket vizsgálni, hogy a színezés során hány különböző színt használunk. 1. eset: Ha 1 színt használunk. Ekkor nyilván 3 jó színezés van. 2. eset: Ha 2 színt használunk. Először eldöntjük, hogy melyik 2 színt használjuk, erre $\left(\genfrac{}{}{0ex}{}{3}{2}\right)=3$ lehetőségünk van. Legyen pl. piros és kék. Ezekből rendre $4+1$; $3+2$; $2+3$ vagy $1+4$ színelosztás lehetséges. A $4+1$ és $1+4$ elosztások mindegyikéből csak 1 lehetőség van a forgásszimmetria miatt. A $3+2$ és $2+3$ elosztásokból a forgásszimmetria miatt rögzítsük a 2 egyforma színűből az egyiket, pl. a szabályos ötszög ,,talpa'' legyen piros. A másik piros helyére 2 lehetőségünk van, ezeket az alábbi ábrák mutatják:     Tehát a 2. esetben összesen $\left(\genfrac{}{}{0ex}{}{3}{2}\right)\cdot \left(2+2\cdot 2\right)=18$ jó színezés van. 3. eset: Ha 3 színt használunk. Ezekből $3+1+1$ vagy $2+2+1$ színelosztás lehetséges. A $3+1+1$ elosztásnál először eldöntjük, hogy melyik színből használunk hármat, erre $\left(\genfrac{}{}{0ex}{}{3}{1}\right)=3$ lehetőségünk van. Legyen pl. piros, ekkor 3 piros, 1 kék és 1 zöld színt használunk fel. A forgásszimmetria miatt rögzítsük a zöld helyét, legyen   az ötszög ,,talpa'' zöld színű. Ekkor a maradék 4 hely bármelyike lehet kék színű és mindegyik különböző esetet jelent. Így a $3+1+1$ elosztásból összesen $\left(\genfrac{}{}{0ex}{}{3}{1}\right)\cdot 4=12$ jó színezés van.     A $2+2+1$ elosztásnál először eldöntjük, hogy melyik színből használunk egyet, erre $\left(\genfrac{}{}{0ex}{}{3}{1}\right)=3$ lehetőségünk van. Legyen pl. piros, ekkor 1 piros, 2 kék és 2 zöld színt használunk fel. A forgásszimmetria miatt rögzítsük a piros helyét, ismét legyen az ötszög ,,talpa'' piros színű. Ekkor, ha a maradék 4 helyet bárhogyan is színezzük 2 kékkel és 2 zölddel, mindig különböző eseteket kapunk. Erre $\left(\genfrac{}{}{0ex}{}{4}{2}\right)=6$ lehetőség van. Így a $2+2+1$ elosztásnál összesen $\left(\genfrac{}{}{0ex}{}{3}{1}\right)\cdot \left(\genfrac{}{}{0ex}{}{4}{2}\right)=18$ jó színezés van. Tehát összesen $3+18+12+18=51$ jó színezése van az ötszögnek.   Megjegyzés. Megmutatható, hogy ha egy szabályos $p$-szöget a feladatbeli feltételeknek megfelelően színezünk $a$ darab színnel, ahol $p$ prím, akkor a jó színezések száma $\frac{a^p-a}{p}+a$.   7. $a)$ A lappföldi Mikulásnak két rénszarvasa van: Vágta és Éppenhogycsak. Ha valamelyik nap Vágta egyedül $x$ sebességgel ($x>1)$ húzná a szánt, akkor Éppenhogycsakot melléfogva az még $1/x$ sebességet tud hozzáadni. A Mikulás már öreg, emiatt ijedős. Minél gyorsabban megy a szán, annál többször fogja vissza az állatokat. A precíz mérések szerint, ha Vágta $x$ sebességgel húzná a szánt, akkor ez éppen $\text{ln}x$ sebességcsökkenést eredményez. Egyszer egy ellenőrzésnél azzal vádolják meg a Mikulást, hogy lassan hajtott. Lappföldön a lassúhajtás határa $7/4$. Meg tudja-e védeni magát a Mikulás? $($Használjuk fel, hogy $\left(\text{ln}x\right)\text{'}=\frac{1}{x}\mathrm{.})$  (9 pont) $b)$ A sakk egy érdekes változata az ún. Fischer random sakk, melyet Robert Fischer amerikai világbajnok hozott létre $1996$-ban. A lényegi eltérés a tisztek $($király (K), vezér (V), $2$ bástya (B), $2$ huszár (H), $2$ futó (F)) elhelyezkedésében rejlik. Az alapállás szabályai: $•$ A király a bástyák között foglal helyet. $•$ A futók ellentétes színű mezőn állnak. A felsorolt tiszteket az alábbi $1\times 8$-as táblázatba kell elhelyezni (az ábrán egy helyes kitöltés látható):     Az azonos minőségű tisztek között (pl. két huszár stb.) csak a futóknál van megkötés arra, hogy szükségszerűen különböző színen kell állniuk. Mutassuk meg, hogy $960$ megengedett alapállás lehetséges a Fischer random sakkban.  (7 pont)   Megoldás. $a)$ A Mikulás akkor tudja magát megvédeni, ha $\forall x\in \left]1;\infty \right[$ esetén $x+\frac{1}{x}-\text{ln}x>1\mathrm{,}75$. Vezessük be az $f:\left]1;\infty \right[\to \text{R}$; $f\left(x\right)=x+\frac{1}{x}-\text{ln}x$ függvényt. A függvényvizsgálatot deriválás segítségével végezzük el. Egy differenciálható függvénynek ott lehet szélsőértéke, ahol $f\text{'}\left(x\right)=0$. $\begin{array}{c}{\displaystyle f\text{'}\left(x\right)=1-\frac{1}{x^2}-\frac{1}{x}=0\to x^2-x-1=0;}\end{array}$ $x_1=\frac{1+\sqrt[]{5}}{2}\approx 1\mathrm{,}618$; $x_2=\frac{1-\sqrt[]{5}}{2}\approx -0\mathrm{,}618$. Minket csak az $\frac{1+\sqrt[]{5}}{2}$ érdekel, mert $D_f=\left]1;\infty \right[$. Mivel $f\text{'}\text{'}\left(x\right)=\frac{2}{x^3}+\frac{1}{x^2}>0$, $\forall x\in \left]1;\infty \right[$ esetén, így az $f$ függvénynek $x=\frac{1+\sqrt[]{5}}{2}$ helyen helyi minimuma van. $\begin{array}{c}{\displaystyle f\left(\frac{1+\sqrt[]{5}}{2}\right)=\frac{1+\sqrt[]{5}}{2}+\frac{1}{\frac{1+\sqrt[]{5}}{2}}-\text{ln}\frac{1+\sqrt[]{5}}{2}\approx 1\mathrm{,}7549>1\mathrm{,}75.}\end{array}$ Tehát a Mikulás biztosan gyorsabban hajtott, mint $\frac{7}{4}$, így képes magát megvédeni. $b)$ Először a futóknak keressük meg a helyüket. Erre $4\cdot 4=16$ lehetőség van, hiszen a világos és sötét mezejű futóknak egymástól függetlenül 4 lehetséges helye van. A maradék 6 helyből megkeressük, hogy hányféleképpen foglalhat helyet a 2 bástya és a király. Ezen figuráknak az egymáshoz való elrendezése rögzített, hiszen a király a 2 bástya között van, továbbá a bástyák között nincs kitüntetettség. Ezek elhelyezésére $\left(\genfrac{}{}{0ex}{}{6}{3}\right)=20$ lehetőség van. A maradék 3 helyre a vezért és a 2 huszárt kell elhelyezni. Ezt nyilván $\left(\genfrac{}{}{0ex}{}{3}{1}\right)=3$-féle módon tehetjük meg. Tehát a figurák elhelyezésére valóban $4\cdot 4\cdot \left(\genfrac{}{}{0ex}{}{6}{3}\right)\cdot \left(\genfrac{}{}{0ex}{}{3}{1}\right)=960$ lehetőség van.   8. $a)$ Egy tizenkét elemű, egész számokból álló mintából ismerünk hét értéket: 4; 4; 4; 5; 7; 9; 13. Tudjuk, hogy a minta egyetlen módusza $5$ és a minta átlagának szórás sugarú környezete három tizedesjegyre kerekítve $\left]\overline{x}-\sigma ;\overline{x}+\sigma \right[=\left]3\mathrm{,}292;8\mathrm{,}708\right[$. Határozzuk meg a minta hiányzó öt elemét.  (8 pont) $b)$ Egyenlő szárú háromszög szára 13 cm, alapja 24 cm. Számítsuk ki a háromszög súlypontjának a háromszög köré írható kör középpontjától való távolságát.   (8 pont)   Megoldás. $a)$ A minta módusza 5 és van 3 darab 4-es benne, ezért az 1 darab 5-ös mellett még biztosan van legalább 3 darab 5-ös. Tehát a minta az alábbi módon néz ki: 4; 4; 4; 5; 7; 9; 13; 5; 5; 5; $x$; $y$, ahol $x\mathrm{,}\mathrm{,}y\in \text{Z}$. Tudjuk, hogy $\overline{x}-\sigma =3\mathrm{,}292$ és $\overline{x}+\sigma =8\mathrm{,}708$. Ezért $\overline{x}=6$ és $\sigma =2\mathrm{,}708$. Mivel $\overline{x}=6$, ezért $\frac{3\cdot 4+4\cdot 5+7+9+13+x+y}{12}=6$, ahonnan $x+y=11$ adódik. Mivel $\sigma =2\mathrm{,}708$, ezért ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\sigma }^2=2\mathrm{,}{708}^2=}\hfill \\ \hfill {\displaystyle =\frac{3\cdot {\left(6-4\right)}^2+4\cdot {\left(6-5\right)}^2+{\left(6-7\right)}^2+{\left(6-9\right)}^2+{\left(6-13\right)}^2+{\left(6-x\right)}^2+{\left(6-y\right)}^2}{12}\mathrm{,}}\hfill \end{array}}$ innen ${\left(6-x\right)}^2+{\left(6-y\right)}^2=13$. Tehát meg kell oldani az ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle x+y}& {\displaystyle =\mathrm{11,}}\hfill & \text{(<mi>I</mi>)}\\ \hfill {\displaystyle {\left(6-x\right)}^2+{\left(6-y\right)}^2}& {\displaystyle =13}\hfill & \text{(<mi>I</mi><mi>I</mi>)}\end{array}}$ egyenletrendszert az egész számok halmazán. Az $y=11-x$ összefüggést beírva a másik egyenletbe, kibontva és rendezve az alábbit kapjuk: $x^2-11x+24=0$. Innen adódik, hogy $x_1=3$; $x_2=8$ és $y_1=8$; $y_2=3$. Tehát a minta hiányzó öt eleme: 3; 5; 5; 5; 8, ezzel a rendezett minta az alábbi módon néz ki: 3; 4; 4; 4; 5; 5; 5; 5; 7; 8; 9; 13. Ellenőrzés a feladat szövege alapján. 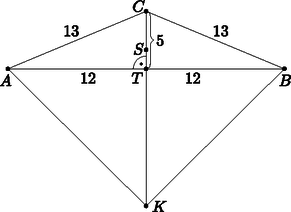$b)$ Készítsünk ábrát a feladathoz. Mivel ${13}^2+{13}^2<{24}^2$, ezért a feladatban szereplő háromszög tompaszögű, így a háromszög köré írt kör középpontja a háromszögön kívül helyezkedik el. Szimmetriaokok miatt a $K$ köré írt kör középpont rajta van a $C$-ből induló magasságvonalon. A háromszög alaphoz tartozó magassága Pitagorasz tétele miatt 5 cm hosszú, melyet a súlypont harmadol, ezért $TS=\frac{5}{3}$ cm. A háromszög területe $T=\frac{24\cdot 5}{2}=60{\text{cm}}^2$, köré írt körének sugara $R=\frac{abc}{4T}=16\mathrm{,}9$ cm. Mivel $R=KC=16\mathrm{,}9$ cm és $SC=\frac{10}{3}$ cm, így a keresett $KS$ távolság $16\mathrm{,}9-\frac{10}{3}=\frac{407}{30}\approx 13\mathrm{,}57$ cm.   9. $a)$ Bence nemrég tanulta az iskolában a szinusztételt és a koszinusztételt. Sajnos rosszul emlékezett rájuk és azokat az alábbi módon jegyezte meg (a jelölések a szokásosak): $\begin{array}{c}{\displaystyle c^2=a^2+b^2+2ab\cdot \text{sin}\gamma \text{és}\frac{a}{b}=\frac{\text{cos}\alpha }{\text{cos}\beta }\mathrm{.}}\end{array}$ Mekkorák annak a háromszögnek a szögei, amelyre igazak a Bence által megtanult összefüggések?  (7 pont) $b)$ Határozzuk meg az $a$; $b$; $c$ egész paraméterek értékét úgy, hogy az $f\left(x\right)=a{x}^2+bx+c$ egyenletű parabola az alábbi feltételek mindegyikét teljesítse. $1.$ $f\text{'}\left(3\right)=-11$. $2.$ $\underset{-1}{\overset{1}{\int }}f\left(x\right)\text{d}x=\frac{2}{3}$. $3.$ Csúcspontja illeszkedik az $y=\frac{1}{2}x+1$ egyenletű egyenesre.  (9 pont)   Megoldás. $a)$ A koszinusztétel szerint $c^2=a^2+b^2-2ab\cdot \text{cos}\gamma$, ezt összevetve Bence formulájával azt kapjuk, hogy $2ab\cdot \text{sin}\gamma =-2ab\cdot \text{cos}\gamma$. Mivel $a;b>0$, ezért $\text{sin}\gamma =-\text{cos}\gamma$ adódik. Ha $\text{cos}\gamma =0$ lenne, akkor $\text{sin}\gamma =0$ adódna, de ez ellentmond a $\text{sin}{}^2\gamma +\text{cos}{}^2\gamma =1$ összefüggésnek. Tehát $\text{cos}\gamma \ne 0$, így oszthatunk vele. Azt kapjuk, hogy $tg\gamma =-1$, innen $\gamma ={135}^{\circ }$ (mivel háromszög belső szögéről van szó). A sinustétel szerint $\frac{a}{b}=\frac{\text{sin}\alpha }{\text{sin}\beta }$, ezt összevetve Bence formulájával azt kapjuk, hogy $\frac{\text{sin}\alpha }{\text{sin}\beta }=\frac{\text{cos}\alpha }{\text{cos}\beta }$. Innen $\frac{\text{sin}\alpha }{\text{cos}\alpha }=\frac{\text{sin}\beta }{\text{cos}\beta }$, azaz $\text{tg}\alpha =\text{tg}\beta$. Mivel háromszög belső szögeiről van szó, ezért $\alpha =\beta$. Mivel $\alpha +\beta +\gamma ={180}^{\circ }$, $\gamma ={135}^{\circ }$ és $\alpha =\beta$, ezért $\alpha =\beta =22\mathrm{,}{5}^{\circ }$ adódik. Tehát a háromszög szögei $22\mathrm{,}{5}^{\circ }$; $22\mathrm{,}{5}^{\circ }$; ${135}^{\circ }$.   Megjegyzés. Az alábbi befejezést is választhattuk volna. A koszinusztételből $\text{cos}\alpha =\frac{b^2+c^2-a^2}{2bc}$ és $\text{cos}\beta =\frac{a^2+c^2-b^2}{2ac}$, így $\begin{array}{c}{\displaystyle \frac{a}{b}=\frac{\text{cos}\alpha }{\text{cos}\beta }=\frac{\frac{b^2+c^2-a^2}{2bc}}{\frac{a^2+c^2-b^2}{2ac}}\mathrm{.}}\end{array}$ Innen $\frac{a}{b}=\frac{a}{b}\cdot \frac{b^2+c^2-a^2}{a^2+c^2-b^2}\to a=b$. Mivel $a=b$, ezért $\alpha =\beta$. Innentől ugyanúgy fejezhető be a feladat, mint előbb.   $b)$ Mivel $f\left(x\right)=a{x}^2+bx+c$, ezért $f\text{'}\left(x\right)=2ax+b$, így $f\text{'}\left(3\right)=6a+b=-11$. A 2. feltétel szerint $\begin{array}{c}{\displaystyle \underset{-1}{\overset{1}{\int }}f\left(x\right)\text{d}x=\underset{-1}{\overset{1}{\int }}\left(a{x}^2+bx+c\right)\text{d}x={\left[a\frac{x^3}{3}+b\frac{x^2}{2}+cx\right]}_{-1}^1=\frac{2a}{3}+2c=\frac{2}{3}\mathrm{,}}\end{array}$ innen $a+3c=1$. Ismert, hogy az $f\left(x\right)=a{x}^2+bx+c$ parabolának $x=-\frac{b}{2a}$ helyen van szélsőértéke, mely egyben csúcspontjának $x$-koordinátája is. Mivel $f(-\frac{b}{2a})=\frac{-b^2+4ac}{4a}$, ezért a parabola csúcspontjának koordinátái: $T(-\frac{b}{2a};\frac{-b^2+4ac}{4a})$, így a 3. feltétel miatt $\frac{-b^2+4ac}{4a}=-\frac{b}{4a}+1$, azaz $b^2+4a=b+4ac$. Feladatunk megoldani az alábbi egyenletrendszert az egész számok halmazán: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle 6a+b}& {\displaystyle =-\mathrm{11,}}\hfill & \text{(<mi>I</mi>)}\\ \hfill {\displaystyle a+3c}& {\displaystyle =\mathrm{1,}}\hfill & \text{(<mi>I</mi><mi>I</mi>)}\\ \hfill {\displaystyle b^2+4a}& {\displaystyle =b+4ac\mathrm{.}}\hfill & \text{(<mi>I</mi><mi>I</mi><mi>I</mi>)}\end{array}}$ Mivel $b=-6a-11$ és $c=\frac{1-a}{3}$, ezért a III. egyenlet így alakul: $\begin{array}{c}{\displaystyle {\left(-6a-11\right)}^2+4a=-6a-11+4a\cdot \frac{1-a}{3}\mathrm{.}}\end{array}$ Ezt összevonva, majd rendezve az alábbi másodfokú egyenletet kapjuk: $\begin{array}{c}{\displaystyle 56a^2+211a+198=0.}\end{array}$ A gyökök: $a_1=-2$; $a_2=\frac{-99}{56}$. Mivel $a;b;c\in \text{Z}$, ezért csak $a=-2$ lehet jó. Ekkor $b=1$ és $c=1$. Tehát $a=-2$; $b=1$; $c=1$. Ellenőrzés a feladat feltételei alapján.