Cím:	Beszámoló a 2019. évi Eötvös-versenyről
Szerző(k):	Tichy Géza ,  Vankó Péter ,  Vigh Máté
Füzet:	2020/február, 106 - 114. oldal	PDF  |  MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén), Hővezetés, Nyugalmi indukció, Kötelek (láncok) dinamikája

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Beszámoló a 2019. évi Eötvös-versenyről   Az Eötvös Loránd Fizikai Társulat 2019. évi Eötvös-versenye október 11-én délután 3 órai kezdettel tizenkét magyarországi helyszínen1 került megrendezésre. Ezért külön köszönettel tartozunk mindazoknak, akik ebben szervezéssel, felügyelettel a segítségünkre voltak. A versenyen a három feladat megoldására 300 perc áll rendelkezésre, bármely írott vagy nyomtatott segédeszköz használható, de (nem programozható) zsebszámológépen kívül minden elektronikus eszköz használata tilos. Az Eötvös-versenyen azok vehetnek részt, akik vagy középiskolai tanulók, vagy a verseny évében fejezték be középiskolai tanulmányaikat. Összesen 56 versenyző adott be dolgozatot, 19 egyetemista és 37 középiskolás. Ismertetjük a feladatokat és azok megoldását.   $*$     1. Egy könnyen mozgó dugattyú egy hőszigetelt, vízszintes tengelyű hengert kezdetben két azonos, $V_0$ térfogatú részre oszt. Mindkét részben $p_0$ nyomású, egyatomos ideális gáz van. A bal oldali részben a kezdeti hőmérséklet $2T_0$, míg a jobb oldali részben $T_0$. A két részt elválasztó dugattyú mérsékelten hővezető, hőátadását az $\alpha$ paraméter jellemzi, azaz $\Delta T$ hőmérséklet-különbség esetén a dugattyún időegységenként átáramló hő $\alpha \Delta T$. $a)$ Mekkora lesz a két részben a gázok térfogata, hőmérséklete és nyomása hosszú idő elteltével? $b)$ Adjuk meg az idő függvényében a két térrészben levő gáz $V_1\left(t\right)$ és $V_2\left(t\right)$ térfogatát! 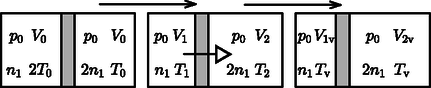(Tasnádi Tamás)   Megoldás. $a)$ Amint a feladat szövege is mutatja, a kezdeti értékeket nulla indexszel, a bal oldali részt egyes, és a jobb oldali részt kettes indexszel jelöljük. A végső állapot mennyiségeit a ,,v'' index mutatja. Az 1. ábra a folyamatot és az állapotjelzők értékeit foglalja össze.     1. ábra   Mivel mindkét részben egyatomos ideális gáz van, a szabadsági fok $f=3$. A kezdeti állapotra felírt gáztörvényből, $\begin{array}{c}{\displaystyle p_0{V}_0=n_{1}R2T_0\mathrm{,}{p}_0{V}_0=n_{2}R{T}_0\mathrm{,}}\end{array}$ megkapjuk, hogy a jobb oldalon a mólok száma kétszer annyi, mint a bal oldalon: $n_2=2n_1$. A dugattyú hőátadása következtében a bal oldali gáz lassan lehűl, és a jobb oldali melegszik, miközben a dugattyú balra tolódik. A folyamat lassúsága következtében a dugattyú két oldalán a nyomásnak meg kell egyeznie, azaz $p_1=p_2$. Továbbá a rendszerben az energia megmarad, tehát a belső energiák összege állandó: $\begin{array}{c}{\displaystyle \frac{f}{2}{n}_{1}R2T_0+\frac{f}{2}2n_{1}R{T}_0=\frac{f}{2}{n}_{1}R{T}_1+\frac{f}{2}2n_{1}R{T}_2\mathrm{,}}\end{array}$ amely egyszerűsítések után, és a gáztörvényt felhasználva: $\begin{array}{c}{\displaystyle p_0{V}_0+p_0{V}_0=p_1{V}_1+p_1{V}_2\mathrm{.}}\end{array}$ A jobb és bal oldali térfogat összege nem változik, és így a fenti egyenletből következik, hogy a nyomás végig mindkét oldalon állandó marad, azaz $\begin{array}{c}{\displaystyle p_1=p_2=p_0\mathrm{,}}\end{array}$ és a folyamat izobár. Most rátérünk a végső állapot meghatározására. Már tudjuk, hogy a végső nyomás megegyezik a kezdetivel. A dugattyún történő hőátadás következtében a végső hőmérséklet a két oldalon ugyanakkora. Az energiamegmaradás $\begin{array}{c}{\displaystyle \frac{f}{2}{n}_{1}R2T_0+\frac{f}{2}2n_{1}R{T}_0=\frac{f}{2}{n}_{1}R{T}_{\text{v}}+\frac{f}{2}2n_{1}R{T}_{\text{v}}}\end{array}$ egyenletéből $\begin{array}{c}{\displaystyle T_{\text{v}}=\frac{4}{3}{T}_0\mathrm{.}}\end{array}$ Gay-Lussac első törvényéből $\begin{array}{c}{\displaystyle V_{1\text{v}}=\frac{2}{3}{V}_0\text{és}{V}_{2\text{v}}=\frac{4}{3}{V}_0\mathrm{.}}\end{array}$ $b)$ Most térjünk rá a folyamat vizsgálatára. A bal oldali rész lehűl, a jobb oldali melegszik, azaz a bal oldal $\Delta t$ idő alatt bekövetkező kicsiny $\Delta T_1$ hőmérséklet-változása negatív, míg a jobb oldalra $\Delta T_2>0$. A folyamat izobár, ezért a bal és jobb oldal egyenlete: $\begin{array}{c}{\displaystyle \frac{f+2}{2}{n}_{1}R\Delta T_1=\alpha \left(T_2-T_1\right)\Delta t\mathrm{,}\text{illetve}\frac{f+2}{2}2n_{1}R\Delta T_2=\alpha \left(T_1-T_2\right)\Delta t\mathrm{.}}\end{array}$ Ezek az egyenletek az $\begin{array}{c}{\displaystyle \frac{f+2}{2}{n}_{1}R\frac{\text{d}{T}_1}{\text{d}t}=\alpha \left(T_2-T_1\right)\mathrm{,}\text{illetve}\frac{f+2}{2}2n_{1}R\frac{\text{d}{T}_2}{\text{d}t}=\alpha \left(T_1-T_2\right)}\end{array}$ differenciálegyenleteknek felelnek meg. Ezekből kifejezve a $\text{d}{T}_1/\text{d}t$ és $\text{d}{T}_2/\text{d}t$ hányadosokat, valamint bevezetve a $\Delta T=T_1-T_2$ hőmérséklet-különbséget $\begin{array}{c}{\displaystyle \frac{\text{d}\Delta T}{\text{d}t}=-\frac{3\alpha }{\left(f+2\right)n_{1}R}\Delta T\text{és}\frac{\text{d}\left(T_1+2T_2\right)}{\text{d}t}=0.}\end{array}$ A második egyenletben a differenciálandó mennyiség nem változik, és kezdeti értékét ismerjük, tehát $\begin{array}{c}{\displaystyle T_1+2T_2=4T_0\mathrm{.}}\end{array}$ Az első egyenletben található állandó a hőátadási folyamat lecsengési együtthatója: $\begin{array}{c}{\displaystyle \lambda =\frac{3\alpha }{\left(f+2\right)n_{1}R}=\frac{6\alpha T_0}{5p_0{V}_0}\mathrm{.}}\end{array}$ A fentihez hasonló differenciálegyenlet a tudományokban számos helyen előfordul. Ezek közül a legismertebb a radioaktív bomlás, amelynek a megoldása a $\lambda$ állandóval lecsengő exponenciális függvény. Mivel ismerjük ennek a függvénynek a kezdeti értékét, ennélfogva $\begin{array}{c}{\displaystyle \Delta T=T_0{\text{e}}^{-\lambda t}\mathrm{,}}\end{array}$ és így $\begin{array}{c}{\displaystyle T_1\left(t\right)=\frac{4}{3}{T}_0+\frac{2}{3}{T}_0{\text{e}}^{-\lambda t}\mathrm{,}{T}_2\left(t\right)=\frac{4}{3}{T}_0-\frac{1}{3}{T}_0{\text{e}}^{-\lambda t}\mathrm{.}}\end{array}$ A térfogatok változását most is Gay-Lussac első törvénye adja: $\begin{array}{c}{\displaystyle V_1\left(t\right)=\frac{2}{3}{V}_0+\frac{1}{3}{V}_0{\text{e}}^{-\lambda t}\mathrm{,}{V}_2\left(t\right)=\frac{4}{3}{V}_0-\frac{1}{3}{V}_0{\text{e}}^{-\lambda t}\mathrm{.}}\end{array}$ Ezeket a függvényeket a 2. ábra grafikonjain is bemutatjuk, ahol a hőmérsékletet $T_0$, a térfogatot $V_0$, az időt pedig $1/\lambda$ egységekben mértük. 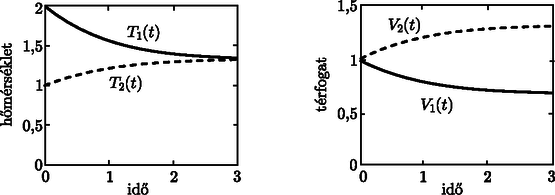 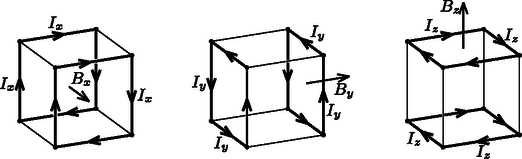   2. ábra     2. Egy $a$ oldalélű kocka minden éle egyforma, $R$ ellenállású huzalból készült. A kocka homogén, kezdetben $B_0$ indukciójú mágneses mezőbe merül, amit $\tau$ idő alatt egyenletesen nullára csökkentünk. Mekkora a folyamat közben keletkező Joule-hő, ha a mágneses indukcióvektor a kocka egy csúcsban találkozó éleivel rendre $\alpha$, $\beta$ és $\gamma$ hegyesszöget zár be? $\left(\text{cos}{}^2\alpha +\text{cos}{}^2\beta +\text{cos}{}^2\gamma =1.\right)$ (Vigh Máté)   Megoldás. Képzeljük el egy pillanatra, hogy a mágneses térnek csak az $x$ irányú, időben $\begin{array}{c}{\displaystyle B_x\left(t\right)=B_{x\mathrm{,0}}\left(1-t/\tau \right)}\end{array}$ szerint változó komponense létezik, a másik két komponens pedig zérus! Ekkor a szimmetria miatt a 3. ábra bal szélén látható árameloszlás jönne létre. A kocka 8 élében folyó, egyforma nagyságú $I_x$ áramokat a Faraday-féle indukciótörvényből lehet meghatározni: $\begin{array}{c}{\displaystyle U_{\text{<span style="font-weight: normal;font-style: normal;">ind</span>}}=-\frac{\text{d}\Phi }{\text{d}t}\to 4R{I}_x=a^2\frac{B_{x\mathrm{,0}}}{\tau }\mathrm{,}}\end{array}$ ahol felhasználtuk, hogy a mágneses tér irányára merőleges lapokon átmenő, kezdeti $a^2{B}_{x\mathrm{,0}}$ nagyságú fluxus $\tau$ idő alatt csökken nullára.     3. ábra   Hasonlóan kapjuk az élekben folyó áramerősségeket azokra az elképzelt esetekre, melyekben a mágneses mezőnek csak az $y$- vagy $z$-komponense van jelen (3. ábra középső és jobb szélső rajza): $\begin{array}{c}{\displaystyle I_x=\frac{a^2}{4R}\frac{B_{x\mathrm{,0}}}{\tau }\mathrm{,}{I}_y=\frac{a^2}{4R}\frac{B_{y\mathrm{,0}}}{\tau }\mathrm{,}{I}_z=\frac{a^2}{4R}\frac{B_{z\mathrm{,0}}}{\tau }\mathrm{.}}\end{array}$   Ha a mágneses térnek mindhárom komponense jelen van, akkor a kialakuló feszültség- és árameloszlást a fenti három eset szuperpozíciójaként kapjuk, ezt mutatja a 4. ábra. A teljes Joule-hő teljesítménye az időben állandó erősségű áramok miatt konstans, nagysága pedig az egyes élekben disszipálódó $R{I}^2$ teljesítmények összege: 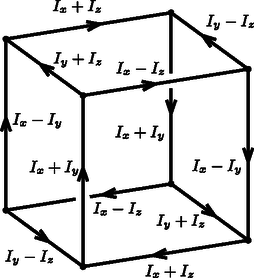${\displaystyle \begin{array}{ccc}\hfill {\displaystyle P}& {\displaystyle =}\hfill & {\displaystyle 2R{\left(I_x+I_y\right)}^2+2R{\left(I_x-I_y\right)}^2+}\hfill \\ \hfill {\displaystyle }& {\displaystyle }\hfill & {\displaystyle +2R{\left(I_y+I_z\right)}^2+2R{\left(I_y-I_z\right)}^2+}\hfill \\ \hfill {\displaystyle }& {\displaystyle }\hfill & {\displaystyle +2R{\left(I_x+I_z\right)}^2+2R{\left(I_x-I_z\right)}^2\mathrm{.}}\hfill \end{array}}$   4. ábra   Ha a zárójeleket felbontjuk, az ${\left(I_x+I_y\right)}^2+{\left(I_x-I_y\right)}^2=2I_x^2+2I_y^2$ összefüggés miatt a teljesítmény az alábbi alakra egyszerűsödik: $\begin{array}{c}{\displaystyle P=8R\left(I_x^2+I_y^2+I_z^2\right)\mathrm{.}}\end{array}$ A keletkező Joule-hőt az előbb kiszámított teljesítmény és a $\tau$ idő szorzataként számolhatjuk. Az $I_x$, $I_y$, $I_z$ áramerősségekre korábban levezetett eredmények felhasználásával kapjuk a következőt: $\begin{array}{c}{\displaystyle Q=P\tau =\frac{a^4}{2R}\frac{B_{x\mathrm{,0}}^2+B_{y\mathrm{,0}}^2+B_{z\mathrm{,0}}^2}{\tau }=\frac{a^4}{2R}\frac{B_0^2}{\tau }\mathrm{.}}\end{array}$ Azt az érdekes eredményt kaptuk, hogy a Joule-hő független a mágneses tér irányától, csupán annak nagyságától függ. A feladatban megadott $\alpha$, $\beta$ és $\gamma$ szögekre tehát nem is volt szükség!   3. Egy nagyon hosszú kötelet vízszintes helyzetben, a súlyánál sokkal nagyobb $F_0$ erővel megfeszítünk. A kötél a pozitív $x$ tengelyen helyezkedik el, egyik vége pedig az origóban van. $a)$ Ha a kötél origóban lévő végét $A$ amplitúdójú, $f$ frekvenciájú harmonikus rezgőmozgással az $x$ tengelyre merőleges, vízszintes $y$ irányban mozgatjuk, a kötélben transzverzális hullámok jönnek létre, amelyek (a kötél hosszegységre eső tömegétől és a feszítettségétől függő) $c$ sebességgel terjednek. (A hullámok amplitúdója kicsi, vagyis $A\ll c/f$.) Adjuk meg a kötél $x$ koordinátájú pontjának $t$ időpillanatbeli $y\left(x\mathrm{,}t\right)$ kitérését! $b)$ Mekkora átlagos teljesítmény szükséges a kötél végének mozgatásához? $c)$ Most a kötél origóban lévő vége $y$ irányban szabadon elmozdulhat, de mozgását a kötél végének $v\left(t\right)$ sebességével arányos, $-\gamma v\left(t\right)$ erő fékezi. A kötélen egy $A$ amplitúdójú szinuszhullám érkezik az origó felé. Azt tapasztaljuk, hogy a hullám részben vagy esetleg teljesen visszaverődik, melynek következtében egy, az origótól távolodó, $B$ amplitúdójú szinuszhullám is kialakul. Mekkora a visszavert hullám amplitúdója? Adjuk meg a $B/A$ arányt! Vizsgáljuk a $\gamma \to \infty$ és $\gamma \to 0$ (nagyon erős és nagyon gyenge csillapítás) eseteket! Van-e olyan $\gamma$ csillapítási tényező, amelynél egyáltalán nem verődik vissza hullám a kötél végéről? (Gnädig Péter)   Megoldás. $a)$ A kötél végpontjának rezgőmozgását az   $\begin{array}{c}{\displaystyle y\left(t\right)=A\text{sin}\left(2\pi ft+{\phi }_0\right)}\end{array}$   függvénnyelírhatjukle,ahol$$ {\phi }_0$$a rezgésfázisaa 0időpillanatban,amelyaz időméréskezdeténekmegfelelőmegválasztásávalnullalehet. Arezgés$c$sebességgelterjedaz $x$ tengelymentén,   $x$ távolságra $\frac{x}{c}$ idő alatt ér el. Így az $x$ koordinátájú pontban a kitérés akkora, mint az origóban $\frac{x}{c}$ idővel korábban volt. Ez alapján a keresett hullámfüggvény: $\begin{array}{c}{\displaystyle y\left(x\mathrm{,}t\right)=A\text{sin}\left[2\pi f\left(t-\frac{x}{c}\right)\right]=A\text{sin}\left(2\pi ft-\frac{2\pi f}{c}x\right)\mathrm{.}}\end{array}$ $b)$ A kötél alakját egy rögzített $t=t_1$ pillanatban az $\begin{array}{c}{\displaystyle y\left(x\right)=y\left(x\mathrm{,}t=t_1\right)=A\text{sin}\left(2\pi f{t}_1-\frac{2\pi f}{c}x\right)}\end{array}$ egyváltozós függvény adja meg, ahol $2\pi f{t}_1$ egy konstans. Bármely $x$ pontban a kötél $x$ tengellyel bezárt szögének tangense éppen ennek a függvénynek a meredeksége, amit legegyszerűbben (az $x$ változó szerinti) deriválással határozhatunk meg: $\begin{array}{c}{\displaystyle \text{tg}\alpha \left(x\mathrm{,}t=t_1\right)=\frac{\text{d}y}{\text{d}x}=-A\frac{2\pi f}{c}\text{cos}\left(2\pi f{t}_1-\frac{2\pi f}{c}x\right)\mathrm{.}}\end{array}$ A kötél alakja azonban változik az idővel, így egy adott ponton a meredekség (és az $\alpha$ szög is) az idő függvénye lesz. Az origóban (az $x=0$ helyen) a kötél iránytangense eszerint: $\begin{array}{c}{\displaystyle \text{tg}\alpha \left(t\right)=\text{tg}\alpha \left(x=\mathrm{0,}t\right)=-A\frac{2\pi f}{c}\text{cos}\left(2\pi ft-\frac{2\pi f}{c}0\right)=-A\frac{2\pi f}{c}\text{cos}\left(2\pi ft\right)\mathrm{.}}\end{array}$ A kötél mozgatásához szükséges (időben változó) pillanatnyi teljesítményt a 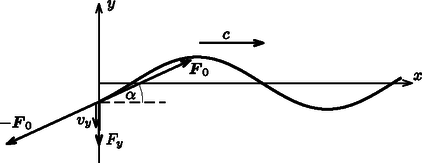$\begin{array}{c}{\displaystyle P\left(t\right)=F_y\left(t\right)v_y\left(t\right)}\end{array}$ szorzat határozza meg, ahol $F_y\left(t\right)$ az általunk a kötél végére kifejtett $y$-irányú erő, $v_y\left(t\right)$ pedig a kötél origóban lévő végének ($y$-irányú) sebessége (5. ábra).     5. ábra   Az $y$-irányú erő (felhasználva, hogy $\alpha \ll 1$): $\begin{array}{c}{\displaystyle F_y=-F_0\text{sin}\alpha \approx -F_0\text{tg}\alpha =F_{0}A\frac{2\pi f}{c}\text{cos}\left(2\pi ft\right)\mathrm{.}}\end{array}$ A kötél végének sebessége a rezgőmozgását leíró $y\left(t\right)=y\left(x=\mathrm{0,}t\right)$ egyváltozós függvény ($t$ szerinti, jól ismert) deriváltja: $\begin{array}{c}{\displaystyle v_y=\frac{\text{d}y}{\text{d}t}=2\pi fA\text{cos}\left(2\pi ft\right)\mathrm{.}}\end{array}$ A pillanatnyi teljesítmény ezek alapján: $\begin{array}{c}{\displaystyle P\left(t\right)=F_y\left(t\right)v_y\left(t\right)=\frac{4{\pi }^2{f}^2{A}^2{F}_0}{c}\text{cos}{}^2\left(2\pi ft\right)\mathrm{.}}\end{array}$   6. ábra   A keresett átlagos teljesítmény ‐ a $\text{cos}{}^2\left(2\pi ft\right)$ függvény 6. ábráról leolvasható, jól ismert átlagértéke alapján ‐ a maximális teljesítmény fele: $\begin{array}{c}{\displaystyle \overline{P}=\frac{P_{\text{max}}}{2}=\frac{2{\pi }^2{f}^2{A}^2{F}_0}{c}\mathrm{.}}\end{array}$ $c)$ Ebben a részben az origó felé érkezik egy hullám. Ennek hullámfüggvénye az ellenkező irányú terjedés miatt: $\begin{array}{c}{\displaystyle y_{\leftarrow }\left(x\mathrm{,}t\right)=A\text{sin}\left(2\pi ft+\frac{2\pi f}{c}x\right)\mathrm{.}}\end{array}$ A visszaverődő hullám ismét a pozitív irányban halad: 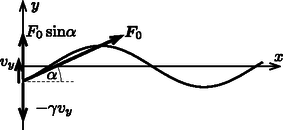  $\begin{array}{c}{\displaystyle y_{\to }\left(x\mathrm{,}t\right)=B\text{sin}\left(2\pi ft-\frac{2\pi f}{c}x+\phi \right)\mathrm{,}}\end{array}$ itt fel kell vennünk egy egyelőre ismeretlen $\phi$ fáziskülönbséget is. A kötélen kialakuló hullám ennek a két hullámnak a szuperpozíciója: $\begin{array}{c}{\displaystyle y\left(x\mathrm{,}t\right)=y_{\leftarrow }\left(x\mathrm{,}t\right)+y_{\to }\left(x\mathrm{,}t\right)\mathrm{.}}\end{array}$   7. ábra   A kötél vége $y$ irányban szabadon mozoghat, így a rá ható $y$-irányú erők eredőjének minden pillanatban nullának kell lennie: $\begin{array}{c}{\displaystyle F_0\text{sin}\alpha -\gamma v_y\approx F_0\frac{\text{d}y}{\text{d}x}-\gamma \frac{\text{d}y}{\text{d}t}=0.}\end{array}$ A hullámfüggvény és a deriváltak: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle y}& {\displaystyle =y_{\leftarrow }+y_{\to }=A\text{sin}\left(2\pi ft+\frac{2\pi f}{c}x\right)+B\text{sin}\left(2\pi ft-\frac{2\pi f}{c}x+\phi \right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{\text{d}y}{\text{d}x}}& {\displaystyle =\frac{2\pi f}{c}A\text{cos}\left(2\pi ft+\frac{2\pi f}{c}x\right)-\frac{2\pi f}{c}B\text{cos}\left(2\pi ft-\frac{2\pi f}{c}x+\phi \right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{\text{d}y}{\text{d}t}}& {\displaystyle =2\pi fA\text{cos}\left(2\pi ft+\frac{2\pi f}{c}x\right)+2\pi fB\text{cos}\left(2\pi ft-\frac{2\pi f}{c}x+\phi \right)\mathrm{.}}\hfill \end{array}}$ Ezeket behelyettesítve az erőegyensúly képletébe, és rendezve: ${\displaystyle \begin{array}{c}\hfill {\displaystyle {F_0\frac{\text{d}y}{\text{d}x}|}_{x=0}={\gamma \frac{\text{d}y}{\text{d}t}|}_{x=0}\mathrm{,}}\hfill \\ \hfill {\displaystyle F_0\frac{2\pi f}{c}A\text{cos}\left(2\pi ft\right)-F_0\frac{2\pi f}{c}B\text{cos}\left(2\pi ft+\phi \right)=}\hfill \\ \hfill {\displaystyle =\gamma 2\pi fA\text{cos}\left(2\pi ft\right)+\gamma 2\pi fB\text{cos}\left(2\pi ft+\phi \right)\mathrm{,}}\hfill \\ \hfill {\displaystyle F_{0}A\text{cos}\left(2\pi ft\right)-F_{0}B\text{cos}\left(2\pi ft\right)\text{cos}\phi +F_{0}B\text{sin}\left(2\pi ft\right)\text{sin}\phi =}\hfill \\ \hfill {\displaystyle \gamma cA\text{cos}\left(2\pi ft\right)+\gamma cB\text{cos}\left(2\pi ft\right)\text{cos}\phi -\gamma cB\text{sin}\left(2\pi ft\right)\text{sin}\phi \mathrm{.}}\hfill \end{array}}$ Ezeknek az egyenleteknek minden időpontban teljesülnie kell, így a $\text{cos}\left(2\pi ft\right)$-s és a $\text{sin}\left(2\pi ft\right)$-s tagokra külön-külön is: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle F_{0}A-F_{0}B\text{cos}\phi }& {\displaystyle =\gamma cA+\gamma cB\text{cos}\phi \mathrm{,}}\hfill \\ \hfill {\displaystyle F_{0}B\text{sin}\phi }& {\displaystyle =-\gamma cB\text{sin}\phi \mathrm{.}}\hfill \end{array}}$ A második egyenlet alapján $\text{sin}\phi =0$, $\phi =0$ (vagy $\phi =\pi$) és így $\text{cos}\phi =1$ (vagy $\text{cos}\phi =-1$). Ezt felhasználva az első egyenlet alapján: $\begin{array}{c}{\displaystyle B=\frac{F_0-\gamma c}{F_0+\gamma c}A\mathrm{.}}\end{array}$ Ha $\gamma \to \infty$ (rögzítjük a kötél végét), akkor $B=-A$, tehát a hullám azonos amplitúdóval, de ellentétes fázisban ($\pi$ fázisugrással) verődik vissza. Ha $\gamma \to 0$ (a kötél vége teljesen szabadon mozog), akkor $B=A$, azaz a hullám szintén azonos amplitúdóval, de most azonos fázisban verődik vissza. $B=0$-t akkor kapunk, ha $\gamma =F_0/c$, ilyenkor tehát egyáltalán nincs visszaverődés.   Megjegyzés. A $b)$ és $c)$ kérdésekre válaszolhatunk energetikai megfontolásokkal is. Ehhez a hullám ‐ mozgási és rugalmas helyzeti energiából származó ‐ energiasűrűségét kell meghatározni.     $*$     Az ünnepélyes eredményhirdetésre és díjkiosztásra 2019. november 22-én délután került sor az ELTE TTK Konferenciatermében. Jelen volt a 70 évvel ezelőtti, háború utáni első Eötvös-verseny győztese, Holics László, aki pár szóban visszaemlékezett erre a versenyre. Meghívást kaptak az 50 és 25 évvel ezelőtti Eötvös-verseny nyertesei is. Az 50 évvel ezelőtti díjazottak közül Láz József volt jelen, a 25 évvel ezelőtti díjazottak közül pedig Horváth Péter, Kovács Krisztián, Tóth Gábor Zsolt és Varga Dezső jött el ‐ ők pár mondatban beszéltek a pályafutásukról. Ezután következett a 2019. évi verseny feladatainak és megoldásainak bemutatása. Az 1. feladat megoldását Tichy Géza, a 2. feladatét Vigh Máté, a 3. feladatét Vankó Péter ismertette. Az esemény végén került sor az eredményhirdetésre. A díjakat Sólyom Jenő, az Eötvös Loránd Fizikai Társulat elnöke adta át. Mindhárom feladat helyes megoldásáért I. díjban részesült Elek Péter, a BME fizika BSc. szakos hallgatója, a Debreceni Református Kollégium Dóczy Gimnáziumának érettségizett tanulója, Tófalusi Péter tanítványa. Két feladat hibátlan megoldásáért, illetve mindhárom feladat kisebb hibákkal való megoldásáért II. díjban részesült Bokor Endre, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 11. osztályos tanulója, Schramek Anikó tanítványa, Fajszi Bulcsú, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 12. osztályos tanulója, Horváth Gábor tanítványa, valamint Fitos Bence, a BME fizika BSc. szakos hallgatója, a Budapesti Németh László Gimnázium érettségizett tanulója, Szászvári Irén és Dégen Csaba tanítványa. Két feladat lényegében helyes megoldásáért III. díjban részesült Csépányi István, a BME fizika BSc. szakos hallgatója, az Egri Szilágyi Erzsébet Gimnázium érettségizett tanulója, Szabó Miklós tanítványa, Máth Benedek Huba, a BME fizika BSc. szakos hallgatója, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium érettségizett tanulója, Horváth Gábor és Nagy Piroska Mária tanítványa, Olosz Adél, a BME építőmérnöki BSc. szakos hallgatója, a PTE Gyakorló Általános Iskola és Gimnázium érettségizett tanulója, Koncz Károly tanítványa, valamint Svastits Domonkos, a BME fizika BSc. szakos hallgatója, a budapesti Piarista Gimnázium érettségizett tanulója, Chikán Éva tanítványa. Egy feladat hibátlan megoldásáért dicséretben részesült Kondákor Márk, a BME fizika BSc. szakos hallgatója, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium érettségizett tanulója, Horváth Gábor és Nagy Piroska Mária tanítványa, Magyar Róbert Attila, a BME fizika BSc. szakos hallgatója, az Egri Dobó István Gimnázium érettségizett tanulója, Hóbor Sándor tanítványa, valamint Pácsonyi Péter, a Zalaegerszegi Zrínyi Miklós Gimnázium 12. osztályos tanulója, Pálovics Róbert tanítványa. Az első díjjal a verseny plakettjén kívül az NKFI Hivatal által nyújtott támogatásból 70 ezer, a második díjjal 50 ezer, a harmadik díjjal 30 ezer, a dicsérettel 20 ezer forint pénzjutalom járt, a díjazottak tanárai és az országos verseny szervezői pedig a Typotex Kiadó könyveit kapták. A verseny megszervezését az Eötvös Loránd Fizikai Társulat ebben az évben szintén az NKFI Hivatal által az Eötvös 100 emlékév alkalmából nyújtott támogatásból fedezte.     ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{<span style="font-weight: bold;">Tichy Géza, Vankó Péter, Vigh Máté</span>}}\hfill \end{array}}$ 1Részletek a verseny honlapján: http://eik.bme.hu/~vanko/fizika/eotvos.htm