Kezdőlap


Cím:	Térbe kilépő bizonyítások I.
Szerző(k):	Kós Géza
Füzet:	2019/október, 391 - 399. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek, Projektív geometria

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Projektív geometriai tételek

Ebben a cikksorozatban olyan bizonyításokat mutatunk be, amikor a geometriai alakzatokat ,,térbe kilépve'', három- vagy akár még magasabb dimenziós objektumok vetületeként vagy metszeteként állítjuk elő.

Az első részben olyan tételeket fogunk vizsgálni, amelyekben csak pontok, egyenesek és ezek illeszkedései szerepelnek, esetleg még egy kör vagy kúpszelet is. Gyakorlott versenyzők számára ezek a tételek jól ismertek, gyakran használjuk versenyfeladatok megoldásához is.

Vetítés az ablaküvegre

Klasszikus ábrázolási módszer, hogy a helyszínt egy üveglapon (ablakon) át nézzük, és az üvegre rajzoljuk rá a tárgyak körvonalait. Valójában a tárgyakat egy pontból ‐ a szemünkből ‐ vetítjük az ablak síkjára. Az ablakkeret a végtelen nagy képből vág ki egy téglalap alakú részletet.
Az ablakkal párhuzamos egyenesek vetületei az ablakon is párhuzamos egyenesek; speciálisan, ha az ablak függőleges irányú, akkor a függőleges egyenesek a képen is függőlegesek. Az ablak síkjával nem párhuzamos egyenesek képei viszont csak félegyenesek (mert nem látjuk a hátunk mögé eső részüket). Az egymással párhuzamos, de az ablakot döfő egyenesek képei egy pontból induló félegyenesek; a közös végpont az üvegen az a pont, ahol a szemünkön keresztül húzott párhuzamos döfi az ablak síkját. Ez a közös ,,iránypont'' az adott irányú ,,végtelen távoli'' vagy ,,ideális'' pont képe.
Különösen műszaki rajzokon fordul elő, hogy csak néhány, esetleg csak háromféle irányt használunk. Attól függően, hogy a fő irányok közül hány (nem) párhuzamos a kép síkjával, beszélhetünk egy, kettő vagy három iránypontos perspektíváról (1., 2. és 3. ábra).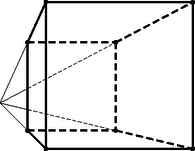

1. ábra. Egy iránypontos perspektíva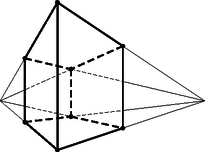

2. ábra. Két iránypontos perspektíva

A rajzórán persze nem meresztjük a szemünket az ablaküvegen keresztül a szomszéd háztömbre; sokkal egyszerűbbnek tűnik, hogy valahogy felvesszük az iránypontokat és néhány további pontot, és vonalzóval elkezdjük összekötögetni. Képzeljük el, hogy a 3. ábrán látható rajzrészletet készítettük el.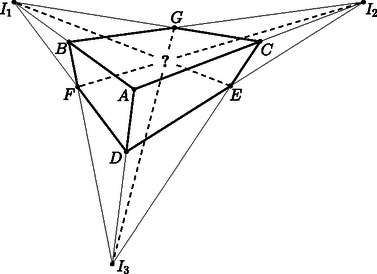

3. ábra. Három iránypontos perspektíva

Ha ez a rajz egy valódi téglatest képe, akkor az

I_{1} E

I_{2} F

és

I_{3} G

egyenesek egy ponton, a téglatest nyolcadik csúcsának képén mennek át. Ha viszont csak úgy, találomra vettünk fel pontokat és húztunk egyeneseket, nem lehetünk biztosak ebben. Márpedig nem szeretnénk megszégyenülve pironkodni, főleg nem a rajztanár előtt. (,,Látod, kisfiam, ha nem csaltál volna, az a három egyenes egy ponton menne át

...

!'') Szerencsére a vetítést visszafelé is el tudjuk végezni, és ki tudunk találni valamilyen térbeli alakzatot, amelynek a rajzrészletünk a vetülete. Azt is meg lehetne próbálni, hogy ,,valódi'' párhuzamosokat találjunk a térben, de erre nem lesz szükség.
Jelöljük

Σ

-val a rajzunk síkját. Vegyünk fel a térben egy új

A'

pontot, ami nincs a

Σ

síkban, de az

Σ

-ra való merőleges vetülete éppen az

A

pont. Az

I_{1} A

I_{2} A

és

I_{3} A

szakaszokon legyen rendre

B'

C'

, illetve

D'

az a belső pont, amelynek merőleges vetülete

Σ

-ra

B

C

, illetve

D

. Az

I_{1} I_{2} A'

háromszögben az

I_{1} C'

és

I_{2} B'

Ceva-szakaszok¹ metszéspontja legyen

G'

. Mivel az

I_{1} C'

és

I_{2} B'

merőleges vetülete

Σ

-n

I_{1} C

és

I_{2} B

, ugyanez igaz a metszéspontjaikra: a

G'

merőleges vetülete

Σ

-n a

G

pont. Hasonlóan, legyen

I_{1} D'

és

I_{3} B'

metszéspontja

F'

, és legyen

I_{2} D'

és

I_{3} C'

metszéspontja

E'

; ezek vetülete

Σ

-n

F

, illetve

E

(4. á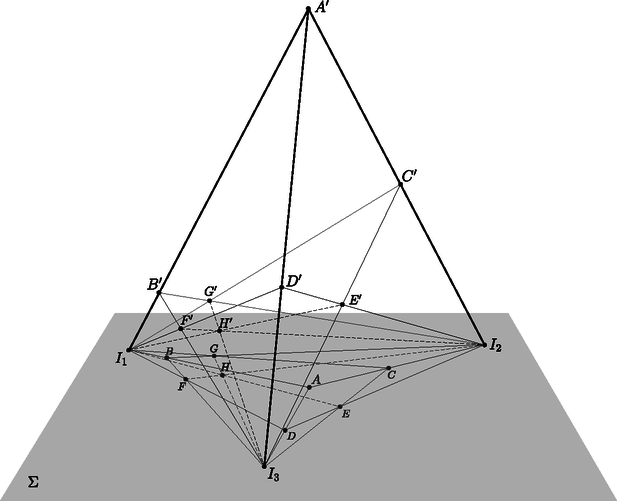bra).

4. ábra. Térbeli rekonstrukció a három iránypontos perspektívából

Most tekintsük az

I_{1} I_{2} D'

I_{1} I_{3} C'

, és

I_{2} I_{3} B'

háromszögek síkjait, jelölje ezeket

Σ_{12}

Σ_{13}

, illetve

Σ_{23}

. A

Σ_{12}

és

Σ_{13}

síkoknak

I_{1}

és

E'

is közös pontja, tehát a két sík metszésvonala az

I_{1} E'

egyenes. Hasonlóan,

Σ_{12}

és

Σ_{23}

metszésvonala az

I_{2} F'

Σ_{13}

és

Σ_{23}

metszésvonala az

I_{3} G'

egyenes.
Az

I_{1} I_{2} D'

háromszögben az

I_{1} E'

és

I_{2} F'

Ceva-szakaszok a háromszög belsejében metszik egymást; a metszéspontjukat jelöljük

H'

-vel. Mivel

I_{1} E'

Σ_{12}

és

Σ_{13}

I_{2} F'

pedig az

Σ_{12}

és

Σ_{23}

síkok metszete, a metszéspont mindhárom síknak közös pontja. Ezért a

H'

ponton a

Σ_{13}

és

Σ_{23}

síkok metszésvonala, az

I_{3} G'

egyenes is átmegy. Ha a

H'

pont

Σ

-ra való vetületét elnevezzük

H

-nak, akkor azt kaptuk, hogy

I_{1} E

I_{2} F

I_{3} G

egyenesek egy ponton,

H

-n mennek át.

Három sík, három egyenes

Az előző bizonyítás fő lépését érdemes általánosabban is végiggondolni és kimondani. A következő tényt nagyon gyakran alkalmazhatjuk térbe kilépő bizonyításokban.

Lemma.² Ha adott három egyenes úgy, hogy közülük bármelyik kettő egy síkban van (tehát metszik egymást vagy párhuzamosak), de a három egyenes együtt nincs egy síkban, akkor a három egyenes vagy egy ponton megy át, vagy pedig párhuzamosak egymással.

A Lemma bizonyítása. Jelölje a három egyenest

e_{1}

e_{2}

és

e_{3}

, és legyen

i = 1,2,3

esetén

Σ_{i, i + 1}

e_{i}

és az

e_{i + 1}

egyenesek síkja. (Szokás szerint ciklikusan indexelünk:

e_{4}

azonos

e_{1}

-gyel, és

e_{5}

azonos

e_{2}

-vel.)
Először is vegyük észre, hogy az

e_{1}

egyenes nem lehet a

Σ_{23}

síkban ‐ mert akkor akkor mindhárom egyenes ebben a síkban lenne ‐, ezért

e_{1}

biztosan különbözik

e_{2}

-től és

e_{3}

-tól. Ugyanígy láthatjuk, hogy

e_{2}

és

e_{3}

egymástól is különbözik. Két különböző egyenesre legfeljebb csak egyféle sík illeszthető, ezért a

Σ_{12}

Σ_{23}

és

Σ_{31}

síkok egyértelműen meghatározottak. Mivel a három egyenes nincs egy síkban, a

Σ_{12}

Σ_{23}

és

Σ_{31}

síkok különbözők. A

Σ_{i + 2, i}

és

Σ_{i, i + 1}

metszésvonala az

e_{i}

egyenes mindegyik

i

indexre.
Két, egy síkban fekvő egyenes vagy párhuzamos, vagy metszi egymást. Ha a három egyenes párhuzamos akkor kész vagyunk, a Lemma állítása teljesül (5. ábra). Ellenkező esetben a három közül valamelyik két egyenes, mondjuk

e_{1}

és

e_{2}

metszi egymást egy

P

pontban. A

P

e_{1}

egyenesen van, ami viszont a

Σ_{12}

és

Σ_{31}

síkok metszete. Ugyanígy a

P

ponton az

e_{2}

egyenes is átmegy, ami a

Σ_{12}

és

Σ_{23}

síkok metszésvonala. A

P

pont tehát mindhárom síkra illeszkedik; emiatt

P

közös pontja a

Σ_{23}

és

Σ_{31}

síkoknak; akkor viszont ezek metszésvonala, a harmadik,

e_{3}

egyenes is átmegy

P

-n (6. ábr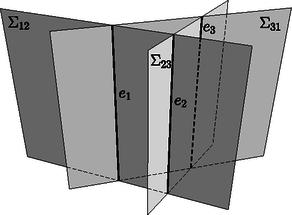a).

5. ábra.

e_{1}

e_{2}

e_{3}

párhuzamosak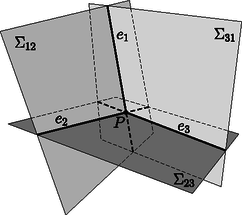

6. ábra.

e_{1}

e_{2}

e_{3}

metszőek

Két klasszikus projektív geometriai tétel

A Lemma alkalmazására két példát mutatunk.

Desargues³ tétele: Legyen

A_{1} A_{2} A_{3}

és

B_{1} B_{2} B_{3}

két háromszög a síkon, amelyek csúcsai és oldalegyenesei is különbözők. Legyen az

A_{1} A_{2}

és

B_{1} B_{2}

egyenesek metszéspontja

X_{12}

, az

A_{1} A_{3}

és

B_{1} B_{3}

egyenesek metszéspontja

X_{13}

, és az

A_{2} A_{3}

és

B_{2} B_{3}

egyenesek metszéspontja

X_{23}

. A következő két állítás ekvivalens:

(a)

A két háromszög megfelelő csúcsait összekötő

A_{1} B_{1}

A_{2} B_{2}

és

A_{3} B_{3}

egyenesek egy ponton mennek át vagy párhuzamosak.

(b)

A két háromszög megfelelő oldalainak metszéspontjai, vagyis az

X_{12}

X_{13}

és

X_{23}

pontok egy egyenesre esnek (7. ábra).
A tétel bizonyítása azon múlik, hogy ez a tíz pontból és tíz egyenesből álló elrendezés egy térbeli geometriai alakzat vetülete (8. ábra).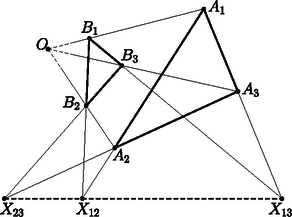

7. ábra. A Desargues-tétel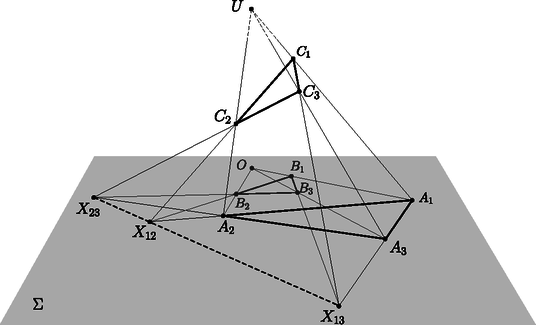

8. ábra. A Desargues-tétel bizonyítása

Az (a)

\Rightarrow

(b) irány bizonyítása:
Az ábra síkját most is jelöljük

Σ

-val. Ha az

A_{1} B_{1}

A_{2} B_{2}

és

A_{3} B_{3}

egyenesek az

O

ponton mennek át, akkor vegyünk fel a térben egy

U

pontot, amelynek merőleges vetülete a

Σ

síkon

O

. Az

U A_{1}

U A_{2}

és

U A_{3}

egyeneseken legyen

C_{1}

C_{2}

, illetve

C_{3}

az a pont, amelynek vetülete

B_{1}

B_{2}

, illetve

B_{3}

. Ha

A_{1} B_{1}

A_{2} B_{2}

és

A_{3} B_{3}

párhuzamosak, akkor vegyünk a térben, az

A_{1}

A_{2}

A_{3}

pontokon keresztül három, egymással párhuzamos egyenest, amelyek merőleges vetülete éppen

A_{1} B_{1}

A_{2} B_{2}

, illetve

A_{3} B_{3}

, és ezeken vegyük fel azokat a

C_{1}

C_{2}

, illetve

C_{3}

pontokat, amelynek vetülete

B_{1}

B_{2}

, illetve

B_{3}

.
Alkalmazzuk most a Lemmát az

A_{1} A_{2}

B_{1} B_{2}

és

C_{1} C_{2}

egyenesekre. Az

A_{1} A_{2}

és

B_{1} B_{2}

egyenesek a

Σ

síkban fekszenek; a

C_{1} C_{2}

B_{1} B_{2}

-n keresztül

Σ

-ra állított merőleges síkban, végül az

A_{1} A_{2}

és

C_{1} C_{2}

egyenesek az

A_{1} C_{1}

és

A_{2} C_{2}

egyenesek síkjában vannak. A

C_{i}

pontok nem lehetnek a

Σ

síkban, mert akkor a teljes

A_{1} C_{1}

egyenes, és vele az

U

pont is

Σ

-ban lenne. A Lemma feltételei teljesülnek: az

A_{1} A_{2}

B_{1} B_{2}

és

C_{1} C_{2}

egyenesek közül bármelyik kettő egy síkban van, de a három egyenes együtt nincs egy síkban. Ezért a három egyenes egy ponton megy át; mivel

A_{1} A_{2}

és

B_{1} B_{2}

X_{12}

pontban metszi egymást, ez azt jelenti, hogy a

C_{1} C_{2}

egyenes is átmegy az

X_{12}

ponton. Az indexek permutálásával ugyanígy láthatjuk, hogy a

C_{13}

egyenes átmegy átmegy

X_{13}

-on, illetve

C_{23}

átmegy átmegy

X_{23}

-on.
Ezek után az

X_{12}

X_{13}

X_{23}

pontok mind közös pontjai az

C_{1} C_{2} C_{3}

és a

Σ

síknak, ezért egy egyenesen vannak.

A (b)

\Rightarrow

(a) irány bizonyítása:
Ugyanezt a térbeli ábrát építjük fel, csak fordított sorrendben. Az

X_{12} X_{13} X_{23}

egyenesen keresztül fektessünk egy

Σ'

síkot, ami különbözik

Σ

-tól, de nem merőleges rá, és ezen jelöljük ki azokat a

C_{1}, C_{2}, C_{3}

pontokat, amelyek

Σ

-ra eső merőleges vetülete

B_{1}

B_{2}

, illetve

B_{3}

. A

C_{1}

C_{2}

X_{12}

pontok közös pontjai az

Σ'

síknak és a

B_{1} B_{2}

egyenesen keresztül

Σ

-ra állított merőleges síknak, ezért egy egyenesre, a két sík metszésvonalára esnek. Ugyanígy látható, hogy

C_{1}

C_{3}

és

X_{13}

, valamint

C_{2}

C_{3}

és

X_{23}

is egy egyenesre esik.
A Lemmát most az

A_{1} C_{1}

A_{2} C_{2}

A_{3} C_{3}

egyenesekre alkalmazzuk. Bármely

1 \leq i < j \leq 3

indexpárra az

A_{i} C_{i}

és

A_{j} C_{j}

egyenesek az

A_{i} C_{i} X_{i j}

síkban vannak, tehát a három egyenes közül bármelyik kettő egy síkban van; ugyanakkor az

A_{1}, A_{2}, A_{3}, C_{1}, C_{2}, C_{3}

pontok nincsenek egy síkban. A Lemma szerint tehát az

A_{1} C_{1}

A_{2} C_{2}

A_{3} C_{3}

egyenesek egy ponton mennek át vagy párhuzamosak. A három egyenest visszavetítve

Σ

-ra látjuk, hogy az

A_{1} B_{1}

A_{2} B_{2}

A_{3} B_{3}

egyenesek egy ponton mennek át vagy párhuzamosak.

Brianchon⁴ tétele: Ha az

A_{1} A_{2} A_{3} A_{4} A_{5} A_{6}

(esetleg hurkolt) hatszög oldalegyenesei érintői egy nem elfajuló kúpszeletnek (kör, ellipszis, parabola vagy hiperbola), akkor a hatszög szemközti pontjait összekötő

A_{1} A_{4}

A_{2} A_{5}

és

A_{3} A_{6}

egyenesek egy ponton mennek át vagy párhuzamosak (9. ábra).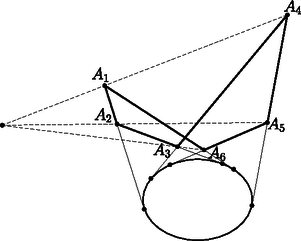

9. ábra. A Brianchon-tétel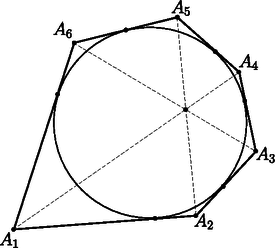

10. ábra. A Brianchon-tétel érintőhatszögben

A tételnek számtalan változatát, speciális és határesetét lehetne felsorolni, az egybeeső oldalegyenesek esetétől a (parabolát érintő) végtelen távoli oldal esetéig. A kedves Olvasónak ajánljuk, hogy valamilyen számítógépes programmal, mint például a GeoGebra, próbáljon minél többféle speciális vagy elfajuló esetet keresni. Itt most nem célunk ezeknek az áttekintése; a tételnek csak az egyik legegyszerűbb esetét fogjuk bizonyítani.

Brianchon tétele, speciális eset: Ha az

A_{1} A_{2} A_{3} A_{4} A_{5} A_{6}

konvex hatszögbe kört lehet írni, akkor a hatszög

A_{1} A_{4}

A_{2} A_{5}

és

A_{3} A_{6}

átlói egy ponton mennek át (10. ábra).

Bizonyítás a speciális esetre. Az ábra síkját most is

Σ

-val fogjuk jelölni. A hatszögbe írt kör érintési pontjai legyenek

T_{1}, ..., T_{6}

a 11. ábra szerint. Válasszunk egy

α

hegyesszöget, és jelöljük ki a térben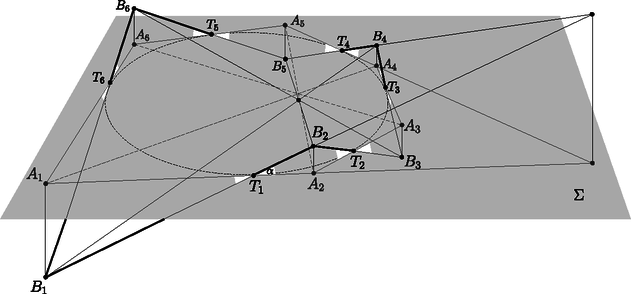

11. ábra. A Brianchon-tétel bizonyítása

azokat a

B_{1}, ..., B_{6}

pontokat, amelyek felváltva

Σ

két oldalán helyezkednek el, merőleges vetületük a

Σ

síkon rendre

A_{1}, ..., A_{6}

, és az

A_{i} T_{i} B_{i} ∢

és

A_{i} T_{i - 1} B_{i} ∢

szögek mindegyike

α

nagyságú. Mivel a körhöz húzott érintő szakaszok egyenlők, mindegyik

i

indexre

A_{i} T_{i} = A_{i} T_{i - 1}

, így az

A_{i} T_{i} B_{i}

és

A_{i} T_{i - 1} B_{i}

derékszögű háromszögek egybevágók, és az

A_{i} T_{i} B_{i} ∢

és

A_{i} T_{i - 1} B_{i} ∢

szögek automatikusan egyenlők. (Úgy is mondhatnánk, hogy a hatszög oldalegyeneseit

Σ

-ra merőlegesen

α

szöggel megdöntjük, és az így kapott egyeneseknek vesszük a metszéspontjait.)
A Lemmát most a

B_{1} B_{4}

B_{2} B_{5}

és

B_{3} B_{6}

egyenesekre alkalmazzuk. A

B_{1} B_{2}

és

B_{4} B_{5}

egyenesek egymás tükörképei a

T_{1} T_{4}

szakasz felező merőleges síkjára, ezért egy síkban vannak; ebben a síkban fekszik a

B_{1} B_{4}

és a

B_{2} B_{5}

egyenes. Ugyanígy láthatjuk, hogy a

B_{2} B_{5}

és

B_{3} B_{6}

, illetve a

B_{3} B_{6}

és

B_{1} B_{4}

egyenesek egy síkban vannak.
Hátra van még annak ellenőrzése, hogy a

B_{1} B_{4}

B_{2} B_{5}

és

B_{3} B_{6}

egyenesek nem lehetnek egy síkban; ez nyilvánvalónak látszik, de formálisabban is igazolhatjuk: ha a

B_{1} B_{4}

B_{2} B_{5}

és

B_{3} B_{6}

egyenesek valamilyen síkban vannak, akkor ebben a síkban vannak a

B_{1}, ..., B_{6}

pontok, a teljes

B_{1} ... B_{6}

töröttvonal, és vele együtt a

T_{1}, ..., T_{6}

pontok is. A

T_{1}, ..., T_{6}

pontok síkja csak a

Σ

lehet, de ez nem lehetséges, mert a

B_{1}

pontokat

Σ

-n kívül vettük fel.
A Lemma feltételei tehát teljesülnek, ezért a

B_{1} B_{4}

B_{2} B_{5}

és

B_{3} B_{6}

egyenesek egy ponton mennek át vagy párhuzamosak. Ugyanez igaz a merőleges vetületeikre, az

A_{1} A_{4}

A_{2} A_{5}

és

A_{3} A_{6}

egyenesekre is. Mivel azonban az

A_{1} A_{4}

A_{2} A_{5}

és

A_{3} A_{6}

átlók közül bármelyik kettő metszi egymást, ez csak úgy lehet, ha a három átló egy ponton megy át.

Ajánlott irodalom

A fenti tételek teljesebb tárgyalásához be kellene vezetnünk a projektív sík és tér ,,ideális'' objektumait, ez most nem volt célunk. Emiatt a tételeket sem mondtuk ki legáltalánosabb formájukban.
Ha valaki szeretne többet tanulni a projektív geometriáról, annak a következő könyveket ajánlom.

[1]	Reiman István: A geometria és határterületei. Gondolat, Budapest, 1986.

[2]	H. S. M. Coxeter: Projektív geometria. Gondolat, Budapest, 1986.

Feladatok

1.	Igazoljuk, hogy a 3. ábrán az $A G$ , $C E$ és $D F$ szakaszok egy ponton mennek át.

2.	Egy perspektivikus képen, csak egyenes vonalzót használva, hogyan jelölhetünk ki egyenlő szakaszokat egy egyenesen? Hogyan többszörözhetünk, felezhetünk vagy harmadolhatunk egy szakaszt?

3.	Vezessük le a Desargues-tételből, hogy a háromszög súlyvonalai egy ponton mennek át.

A B C

háromszög beírt köre az oldalakat az

A_{1}

B_{1}

C_{1}

pontokban érinti. Jól ismert, hogy az

A A_{1}

B B_{1}

C C_{1}

Ceva-szakaszok egy ponton, a háromszög Gergonne-pontján mennek át. Gondoljuk meg, hogy ez a tény a Brianchon-tételnek milyen elfajuló esete, és igazoljuk közvetlenül, térbe kilépéssel is.

5.	Az $A B C D$ érintőnégyszög beírt köre az $A B$ , $B C$ , $C D$ , $D A$ oldalakat rendre az $E$ , $F$ , $G$ , illetve $H$ pontban érinti. Mutassuk meg, hogy az $A C$ , $B D$ , $E G$ és $F H$ szakaszok egy ponton mennek át.

Legyen

A_{1} A_{2} A_{3} A_{4} A_{5} A_{6}

érintőhatszög, legyen az

A_{1} A_{3}

és

A_{4} A_{6}

egyenesek metszéspontja

P

, az

A_{2} A_{4}

és

A_{5} A_{1}

egyenesek metszéspontja

Q

, az

A_{3} A_{5}

és

A_{6} A_{2}

egyenesek metszéspontja

R

. Mutassuk meg, hogy a

P

Q

és

R

pontok egy egyenesen vannak.

¹Olyan szakaszok, amelyek a háromszög egyik csúcsát a szemközti oldal egyik pontjával kötik össze.

²A görög ,, $λ \overset{´}{η} μ μ α$ '' szó jelentése kapott valami, például ajándék, profit vagy korrupt pénz. Matematikában olyan állítást, tételt jelent, ami nem önmagában érdekes, hanem más tételek bizonyításához használjuk fel. A ,,lemma'' helyett a ,,segédtétel'' vagy ,,segédállítás'' szavakat is írhatnánk.

³Gérard Desargues francia matematikus és építész, 1591‐1662.

⁴Charles Julien Brianchon francia matematikus, 1783‐1864.