Cím: A 60. Nemzetközi Matematikai Diákolimpia feladatainak megoldása I.
Szerző(k):  Schrettner Jakab ,  Szabó Kristóf ,  Zsigri Bálint 
Füzet: 2019/október, 386 - 391. oldal  PDF  |  MathML 
Témakör(ök): Cikkek, Nemzetközi Matematikai Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A hagyományoknak megfelelően ebben az évben is közöljük a nyári matematikai diákolimpia feladatainak a megoldásait; lényegében úgy, ahogyan a legilletékesebbek, a magyar csapat tagjai leírták. Közreműködésüket köszönjük és ezúton is gratulálunk eredményeikhez.

 

 
A szerkesztőség

 
Első nap*

 
1. Jelölje Z az egész számok halmazát. Határozzuk meg az összes olyan f:Z→Z függvényt, amelyre minden egész a, b esetén teljesül
f(2a)+2f(b)=f(f(a+b)).


 
Szabó Kristóf megoldása. Jelölje P(a,b) a függvényegyenletet:
P(a,b):f(2a)+2f(b)=f(f(a+b))∀a,b∈Z.
Minden függvényegyenletet érdemes behelyettesítések kipróbálásával elkezdeni. Esetünkben a 0 egy olyan helyettesítési érték, amely a képletben szereplő kifejezéseket jelentősen leegyszerűsíti:
P(0,b):f(0)+2f(b)=f(f(b)),(1)P(a,0):f(2a)+2f(0)=f(f(a))=(1)f(0)+2f(a),(2)f(2a)=2f(a)-f(0).(2.1)
A (2)-nél felhasználtuk az (1) egyenletet, majd rendezéssel kaptuk a (2.1)-et. Az (1) és (2.1)-es egyenlettel jelentősen leegyszerűsíthető az eredeti P egyenlet:
2f(a)-f(0)+2f(b)=(2.1)f(2a)+2f(b)=f(f(a+b))=(1)2f(a+b)+f(0),f(a)+f(b)=f(a+b)+f(0).(3)


Ebből minden n pozitív egészre:
f(n)=f(n-1)+f(1)-f(0)=f(n-2)+2f(1)-2f(0)=...==n(f(1)-f(0))+f(0);
hasonlóan, ha n negatív:
f(n)+f(1)=f(n+1)+f(0)=...=n(f(1)-f(0))+f(0).
Legyen u=f(1)-f(0) és v=f(0). (Mivel f(0),f(1) egészek voltak, így u és v is az.) Az előzőek alapján f(n)=un+v. Visszahelyettesítve az eredetibe (P):
2ua+v+2ub+2v=u2(a+b)+uv+v.(4)
Az a, b helyére 0-t helyettesítve:
3v=(u+1)v.(4.1)
Ezt kivonva a (4)-ből kapjuk, hogy:
2u(a+b)=u2(a+b).
Ebből következik, hogy 2u=u2, tehát u=0 vagy 2.
Ha u=0, akkor (4.1) miatt v=0, tehát f(n)=0.
Ha u=2, akkor tetszőleges v-re f(n)=2n+v megoldás lesz. Ellenőrzés:
4a+v+4b+2v=2(2(a+b)+v)+v=4a+4b+3v.

Ezzel megadtuk az összes lehetséges f függvényt.
 
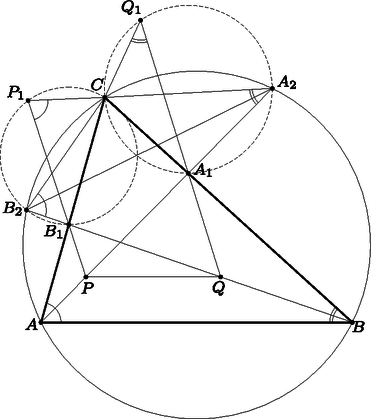
2. Az ABC háromszögben A1 a BC oldalon, B1 pedig az AC oldalon fekszik. Legyenek P és Q rendre az AA1 és BB1 szakaszok olyan pontjai, amelyekre PQ párhuzamos AB-vel. Legyen P1 a PB1 egyenes egy olyan pontja, amire B1 a PP1 szakasz belsejében fekszik, és PP1C∢=BAC∢. Hasonlóan legyen Q1 a QA1 egyenes egy olyan pontja, amire A1 a QQ1 szakasz belsejében fekszik, és CQ1Q∢=CBA∢.
Bizonyítsuk be, hogy a P, Q, P1, Q1 pontok egy körön fekszenek.
 
 
 

 
Schrettner Jakab megoldása. Legyen az AA1 és BB1 egyenesek második metszéspontja az ABC háromszög körülírt körével rendre A2 és B2. Szögszámolással kapjuk, hogy
CA2A1∢=CA2A∢=CBA∢=CQ1Q∢=CQ1A1∢,
felhasználva, hogy A2 és B2 is az ABC körön vannak. Ebből következik, hogy C, A1, A2, Q1 egy körre esnek. Hasonlóan kaphatjuk, hogy C, B1, B2, P1 is egy körre esnek.
Mivel PQ párhuzamos AB-vel, illetve a fentebb kapott húrnégyszögek miatt
QPA2∢=BAA2∢=BB2A2∢=QB2A2∢,
így P, Q, A2, B2 egy körre esnek. Továbbá
P1PA2∢=PB1A∢+B1AP∢=P1B1C∢+CAA2∢=P1B2C∢+CB2A2∢==P1B2A2∢.
Azaz P1, B2, P, A2 egy körre esnek. Így P1 is rajta van a P, Q, A2, B2 pontokat tartalmazó körön. Ugyanezen szögszámolást elvégezve a másik oldalon kapjuk, hogy Q1, A2, Q, B2 is egy körre esnek, tehát Q1 is rajta van a P, Q, A2, B2 pontokat tartalmazó körön.
Azt kaptuk tehát, hogy a P, Q, P1, Q1, A2, B2 pontok mind egy körre esnek, amiből a feladat állítása is következik.
 
3. Egy szociális hálózatnak 2019 tagja van, közülük némely párok barátai egymásnak. Ha A barátja B-nek, akkor B is barátja A-nak. A következő típusú esemény előfordulhat többször egymás után, egy időben mindig csak egy ilyen esemény történik:
 

Ha A, B, C olyanok, hogy A barátja B-nek is és C-nek is, de B nem barátja C-nek, akkor barátságot változtathatnak úgy, hogy B és C most már barátai egymásnak, A és B, valamint A és C barátsága viszont megszűnik. Az összes többi barátság változatlan marad.
 

Kezdetben 1010 olyan tag van, amelyek mindegyikének pontosan 1009 barátja van, és 1009 olyan tag, amelyek mindegyikének pontosan 1010 barátja van. Bizonyítsuk be, hogy létezik a fenti típusú eseményeknek egy olyan sorozata, amelyek végén minden tagnak legfeljebb egy másik tag a barátja.
 
Zsigri Bálint megoldása. Gondoljunk a problémára egy gráfként.
Vegyük észre, hogy minden lépésben az élek száma eggyel csökken, és hogy bármely csúcs fokszámának a paritása állandó marad. Figyeljük meg továbbá a kiinduló gráf következő tulajdonságait. A gráfban nem lehet teljes gráf komponens, mert annak 1010 vagy 1011 csúcsúnak kéne lennie (hiszen minden csúcs fokszáma 1009 vagy 1010), vagyis csak 1010 csúcsú lehet: az 1010 darab 1009 fokú csúcs; viszont ekkor tetszőleges 1010 fokú csúcsra igaz, hogy mivel csak 1008 másik ilyen van, ezért össze van kötve 1009 fokúval is, ami ellentmondás. Az előzőek alapján szintén igaz, hogy a gráf minden komponensében van páratlan fokú csúcs. Tehát a kiinduló gráf olyan komponensekből áll, melyek mindegyike az alábbi három kategória egyikébe esik:
1.Izolált pont (eredetileg 0 darab).
2.2 csúcsú teljes gráf (eredetileg 0 darab).
3.Egyéb nem teljes gráf, mely tartalmaz páratlan fokú csúcsot.

Ha van 3. típusú komponens, akkor nyilván tudunk lépni. Belátom, hogy ekkor olyat is tudunk lépni, amellyel továbbra is csak ilyen komponensek maradnak.
1.Tegyük fel, hogy tudunk olyat lépni, hogy azzal a gráf adott komponense továbbra is összefüggő marad.
Ekkor ez a komponens továbbra is tartalmazni fog páratlan fokú csúcsot (mivel a csúcsok fokszámainak paritása állandó), és a többi komponens változatlan marad; tehát csak annyit kell belátni, hogy ez a komponens nem alakul teljes gráffá. Ehhez vizsgáljuk meg, hogyan keletkezhet teljes gráf.
Ha egy izolált teljes gráf komponens keletkezik, akkor a keletkező komponens egyik csúcsának benne kellett lennie abban a három csúcsban, amelyre a lépést végrehajottuk.
a)Ha csak az egyik csúcsa volt benne a keletkező teljes gráfnak a csúcshármasban, akkor az lehetett a cseresznye egyik vége, vagy a középső csúcs.
i)Ha a cseresznye egyik vége benne volt a keletkező teljes gráfban, de a másik tehát nem (a cseresznyének csak 1 csúcsa volt benne!), akkor a keletkező komponens nem lesz izolált teljes gráf, mivel a cseresznye másik vége egy éllel hozzá lesz kötve (ellentmondásra jutunk).
ii)Ha a cseresznyének a közepe van benne a keletkező teljes gráfban, akkor a cseresznyének a két vége a keletkező teljes gráf semelyik másik csúcsával sincs összekötve (hiszen izolált lesz a teljes gráf), tehát ők ezen lépés után elszakadnak. Mivel az 1. pontban vagyunk, ezért ez jelen esetben ellentmondásra vezetne (nem maradna a komponens összefüggő).

b)Ha két csúcsa is benne van a csúcshármasnak a keletkező teljes gráfban, akkor azok közt eredetileg nem lehetett él, hiszen a lépés után muszáj köztük élnek lenni. Ekkor a cseresznye közepe nyilván nem lehetett benne a teljes gráfban, és nem is lehetett összekötve annak egyéb csúcsaival, tehát a lépés után ő elszakad tőle. Mivel az 1. pontban vagyunk, ezzel a lehetőséggel szintén nem kell törődnünk.

Tehát ilyen esetben izolált teljes gráf komponens nem keletkezhet.
2.Tegyük fel most, hogy csak olyat tudunk lépni, hogy attól egy komponens kettészakad.
a)Tételezzük fel, hogy van olyan 2 fokú csúcs, amely egy lehetséges lépésben a cseresznye közepe.
Ekkor ezt a lépést végrehajtva ő elszakad, és 1. típusú komponens lesz, valamint a volt komponensének maradékában továbbra is lesz páratlan fokú csúcs (hiszen minden csúcs fokszámának paritása állandó). A komponensének a maradéka így vagy nem lesz teljes gráf, és ezzel 3. típusú lesz, vagy
i)2 csúcsú teljes gráf lesz, vagyis 2. típusú.
ii)Tegyük fel, hogy 3 csúcsú teljes gráf lesz.
Ekkor az eredeti komponens egy 4 csúcsú kör volt, ami ellentmond az indukciós feltevésnek, mert a 3 kategória egyikébe sem esik bele. Ezzel tehát nem kell törődnünk.
iii)Tegyük fel, hogy legalább 4 csúcsú teljes gráf lesz.
Ekkor a csúcs, mely elszakad, eredetileg egy-egy éllel volt hozzákötve egy teljes gráfhoz, melynek egy éle (értelemszerűen) hiányzott. Ez az izolált teljes gráfok keletkezési lehetőségeinek fentebb tárgyalt módjaiból következik, és abból, hogy a cseresznye közepe 2 fokú. Ha viszont ebben az esetben egy olyan cseresznyével lépnénk, aminek a közepe az eredeti cseresznyénk egyik vége, és az egyik vége az eredeti cseresznyénk közepe (ő a teljes gráf semelyik másik csúcsával nincs összekötve, kivéve azt az egyet, amellyel az új középső nincs összekötve), akkor a komponens nem szakadna ketté (maradna a cseresznyén kívül 2 összekötött csúcs, amik együtt mindenkivel össze vannak kötve; az egyik az eredeti cseresznye másik vége, a másik pedig akármelyik másik). Mivel a 2. részben vagyunk, ez ellentmondás, és nem történhet meg.
Tehát a tulajdonság az a) esetben valóban megmarad.
b)Most azt tegyük fel, hogy minden cseresznye, amivel lehet lépni legalább 3 fokú középső csúccsal rendelkezik.
Legyen egy tetszőleges ilyen cseresznye középső csúcsa A, két vége pedig B és C, továbbá D az A-nak egy B-től és C-től különböző szomszédja. Mivel a BAC cseresznyével lépve (ahol A a középső csúcs) a komponens kettészakad, ezért B és D, illetve C és D közt nem futhat él (hiszen A-nak és B-nek, illetve A-nak és C-nek különböző komponensbe kell kerülnie), és minden köztük futó út átmegy A-n. Tehát a BAD és CAD cseresznyékkel is léphetünk. Ha ezek közül az egyikkel lépünk, akkor A és D különböző komponensekbe kerülnek, így A bármely másik szomszédja és D közt csak A-n keresztül vezethet út. Ugyanebből a lépésből ismert, hogy B és C közt is csak A-n keresztül mehet út.
Ebből általánosságban tudjuk, hogy A (aki tetszőleges cseresznye-közép volt!) bármely két csúcsa közt csak A-n keresztül vezethet út. Vagyis A-t elhagyva a gráfból minden szomszédja külön komponensbe kerül. Tekintsünk egy tetszőleges ilyen komponenst.
Ismert, hogy egy gráfban a fokszámok összege mindig páros, vagyis páros sok páratlan fokú csúcs van benne. A kiválasztott komponensünkbe viszont megy még kívülről egy él (A-ból), ami egy csúcs fokának a paritását megváltoztatja, vagyis páratlan sok páratlan fokú csúcsnak kell lennie egy ilyen leendő komponensben, tehát lennie kell páratlan fokú csúcsnak.
Mivel a kettészakadás után mindkét komponensben benne lesz egy-egy teljes ilyen komponens (legalább 3 ág van!), ezért mindkettőben lesz páratlan fokú csúcs. Így mindkét komponensre igaz, hogy vagy 2. típusú, vagy csak annyit kell róla belátni, hogy nem izolált teljes gráf. Tegyük fel indirekt módon, hogy mégis teljes gráf keletkezik.
i)Ha az 1./a)/ii) módon keletkezik a teljes gráf, akkor ezen cseresznye helyett azzal lépve, amelynek a közepe az eredeti közepe, egyik vége az eredeti egyik vége, és a másik vége a keletkező teljes gráf egyik csúcsa, a komponens nem szakadna ketté; tehát nem a 2. részben lennénk.
ii)Ha az 1./b) módon keletkezik a teljes gráf, akkor az eredeti cseresznye helyett azzal lépve, amelynek a közepe az eredeti egyik vége, egyik vége az eredeti közepe, a másik vége pedig a keletkező teljes gráfban van, a komponens nem szakadna ketté, és ekkor sem a 2. részben vagyunk.

Tehát egyik keletkező komponens nem lehet teljes gráf, vagyis 2. vagy 3. típusú.
Beláttuk tehát, hogy ha tudunk lépni, akkor tudunk úgy lépni, hogy minden komponens beleessen a fent felsorolt 3 kategória egyikébe, viszont csak akkor nem tudunk lépni, ha csak 1. és 2. típusú komponensek maradtak. Mivel minden lépésben az élek száma eggyel csökken, és kezdetben csak véges sok él volt, ezért csak véges sokat tudunk így lépni, vagyis előbb-utóbb a fent leírt állapotba jutunk, ami a feladat által leírt állapot. Tehát a feladat által meghatározott állapotba biztosan el tudunk jutni.
*A második nap feladatainak megoldását a novemberi számban közöljük.