Cím: Megoldásvázlatok a 2019/5. szám emelt szintű matematika gyakorló feladatsorához
Szerző(k):  Varga Péter 
Füzet: 2019/május, 270 - 283. oldal  PDF  |  MathML 

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. rész
 

 
1. a) A 2, 0, 1, 9 számjegyekből az összes lehetséges módon háromjegyű természetes számokat képeztünk. Számítsuk ki annak a valószínűségét, hogy a képzett számok közül egyet véletlenszerűen kiválasztva, annak számjegyei különbözők.
  (3 pont) b) Oldjuk meg a [π2;π] halmazon a sin(x+2019π)=-12 egyenletet.  (8 pont)
 
Megoldás. a) A képzett számok első számjegye háromféle (2, 1 vagy 9), második és harmadik számjegye négyféle (2, 0, 1, vagy 9) lehet, ezért az összes lehetőség száma (az előbbiek szorzata, azaz) 3⋅42=48. A megadott számjegyekből 32⋅2=18 különböző számjegyekből álló háromjegyű szám képezhető.
Ez a kedvező esetek száma. Így a keresett valószínűség: 1848=38.
b) I. megoldás. Az addíciós tétel alapján:
sinx⋅cos(2019⋅π)+cosx⋅sin(2019⋅π)=-12.
sinx⋅(-1)+cosx⋅0=-12. Az egyenletet rendezve: sinx=12. Ebből x=π6+2kπ, k∈Z, vagy x=5π6+2lπ, l∈Z. A megadott alaphalmazon csak x=5π6 megoldás.
Ellenőrzés behelyettesítéssel, vagy az ekvivalens átalakításokra hivatkozással.
II. megoldás. A szinusz függvény periodicitása miatt: sin(x+1009⋅2⋅π+π)=-12, sin(x+π)=-12. Az egyenletet x-re megoldva: x+π=7π6+2kπ, k∈Z.
Ebből (az egyik gyök) x=π6+2kπ, k∈Z. Az egyenletet x-re megoldva: x+π=11π6+2lπ, l∈Z. Ebből (a másik gyök) x=5π6+2lπ, l∈Z. A megadott alaphalmazon csak x=5π6 megoldás.
Ellenőrzés behelyettesítéssel, vagy az ekvivalens átalakításokra hivatkozással.
III. megoldás. Az egyenletet x-re megoldva: x+2019⋅π=7π6+2kπ, k∈Z.
Ebből az egyik gyök x=π6+2kπ, k∈Z. Az egyenletet x-re megoldva:
x+2019⋅π=11π6+2lπ,l∈Z.
Ebből a másik gyök x=5π6+2lπ, l∈Z. A megadott alaphalmazon csak x=5π6 megoldás.
Ellenőrzés behelyettesítéssel, vagy az ekvivalens átalakításokra hivatkozással.
 

 
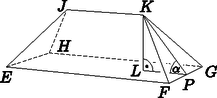
2. A Regéci Vár egy 1300 körül épült vár, ahol II. Rákóczi Ferenc fejedelem a gyermekkorát töltötte. Az 1. ábrán ennek a várnak a XIV. századi állapota látható, a 2. ábrán pedig egy vázlatos képet láthatunk annak tornyáról.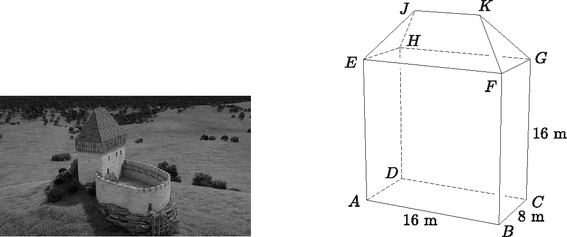

1. ábra        2. ábra

A torony az ABCDEFGH téglatestből és az EFGHJK tetőből áll. A tornyot alkotó téglatest külső méretei: AB=16 m, BC=8 m és CG=16 m.
a) Mekkora az oldalfalak térfogata, ha a fal vastagsága 2 m és az összes faltérfogatot az ablakok, ajtók és lőrések 5%-kal csökkentik?  (4 pont) Tudjuk, hogy az EFGHJK tető magassága 5 méter, és az EJH és FKG egyenlő szárú háromszögek síkjai 50∘-os szöget zárnak be az EFGH síkkal.
b) Mekkora a JK szakasz hossza?  (5 pont) A vár 2018-as rekonstrukciója során gimnazisták több napon keresztül segítették a régészek munkáját. A diákok 60%-a ásásban, 30%-a feltárásban, és 45%-a talicskázásban segített. Egyféle munkát 29-en végeztek, pontosan kétféle munkafolyamatban a tanulók 15 része, mindháromban pedig 7,5%-a vett részt.
c) Hány tanuló vett részt összesen a munkálatokban?  (3 pont)
 
Megoldás. a) I. megoldás. Az ABCDEFGH téglatest térfogata:
VABCDEFGH=16⋅8⋅16=2048(m3).
A belső téglatest 12 m hosszú, 4 m széles és 16 m magas, így ennek térfogata: Vbelső=12⋅4⋅16=768(m3).
Az oldalfalak térfogata: V=VABCDEFGH-Vbelső=2048-768=1280(m3), melyet az ablakok, ajtók és lőrések miatt 5%-kal csökkentve a keresett térfogat 1280⋅0,95=1216m3 lesz.
II. megoldás. A hosszabbik oldalfal 16 m hosszú, 16 m magas és 2 m vastag, így ennek térfogata: V1=16⋅16⋅2=512(m3). A rövidebbik oldalfal 4 m hosszú, 16 m magas és 2 m vastag, így ennek térfogata: V2=4⋅16⋅2=128(m3).
Mivel a hosszabbik és a rövidebbik oldalfalból kettő van, így a teljes térfogat: V=(512+128)⋅2=1280(m3), melyet az ablakok, ajtók és lőrések miatt 5%-kal csökkentve a keresett térfogat 1280⋅0,95=1216m3 lesz.
 

b) Az EFGHJK tető magassága a tető K csúcsából az EFGH síkra bocsátott merőleges szakasz. Az EFGHJK tető K csúcsából induló magasságát és az FKG háromszög alaphoz tartozó magasságát behúzva, a tető és az EFGH sík hajlásszöge α.

Az LPK derékszögű háromszögben: tg50∘=5LP, ahonnan LP=5tg50∘(≈4,2m).
Mivel a tető szimmetrikus, ezért JK=16-2⋅5tg50∘≈7,61 m hosszú.
c) I. megoldás. Jelölje x a munkálatokban részt vevő tanulók számát. Ekkor:
  mindhárom munkafolyamatban0,075x;pontosan két munkafolyamatban0,2x;pontosan egy munkafolyamatban29 tanuló vesz részt.  

Ebben az esetben tehát az egyenlet: 0,075x+0,2x+29=x. Ebből x=40.
II. megoldás. Jelölje x a munkálatokban részt vevő tanulók számát. Ha az egyes munkafolyamatokat összegezzük, akkor egyszeresen számoltuk azokat, akik csak egyféle, kétszeresen, akik kétféle, és háromszorosan azokat, akik mindhárom tevékenységet végezték.
Ebben az esetben tehát az egyenlet: 1,35x=29+2⋅0,2x+3⋅0,075x. Ebből x=40.
 

 
3. a) Oldjuk meg az alábbi egyenlőtlenséget a valós számok halmazán.
log2x≤log12(4x)(7 pont)

b) Oldjuk meg az alábbi egyenletrendszert, ahol x és y nemnegatív valós számok.
x-y=8,xy=33.}(7 pont)

 
Megoldás. a) I. megoldás. A két logaritmus csak akkor értelmezhető, ha x>0. A két oldalt azonos alapra hozva:
log2x≤log2(4x)log212.
A logaritmus azonossága alapján: log2x≤log2(4x)-1. A logaritmusfüggvény szigorú monotonitása vagy kölcsönös egyértelműsége miatt: x≤14x.
Mivel x>0, így az egyenlőtlenséget rendezve: x2≤14. Ebből -12≤x≤12, melyet az értelmezési tartománnyal összevetve az egyenlőtlenség megoldáshalmaza ]0;12].
II. megoldás. A két logaritmus csak akkor értelmezhető, ha x>0. A két oldalt azonos alapra hozva:
log2x≤log2(4x)log212.
A nevezővel beszorozva: -log2x≥log2(4x). A logaritmus azonossága alapján: -log2x≥log24+log2x. Az egyenlőtlenséget rendezve: log2x≤-1(=log212).
A logaritmusfüggvény szigorú monotonitása vagy kölcsönös egyértelműsége miatt: x≤12, melyet az értelmezési tartománnyal összevetve az egyenlőtlenség megoldáshalmaza ]0;12].
b) I. megoldás. Mindkét egyenletet négyzetre emelve:
x-2xy+y=64,xy=1089.
A második egyenletet az elsőbe helyettesítve kapjuk, hogy x+y=130, ahonnan y=130-x. A második egyenletből y=130-x helyettesítéssel: x2-130x+1089=0. Ebből x1=121 és x2=9, majd visszahelyettesítve y1=9 és y2=121.
Ellenőrzés behelyettesítéssel:
x1=121 és y1=9 megoldása az egyenletnek;
x2=9 és y2=121 nem megoldása az egyenletnek.
II. megoldás. A gyökvonás azonossága alapján:
x-y=8,x⋅y=33.
Az első egyenletből: y=x-8, melyet a második egyenletbe helyettesítve: x-8x-33=0. Ebből (x)1=11 és (x)2=-3. Az egyenlet gyökei: x1=121 és x2=9, majd visszahelyettesítve y1=9 és y2=121.
Ellenőrzés behelyettesítéssel:
x1=121 és y1=9 megoldása az egyenletnek;
x2=9 és y2=121 nem megoldása az egyenletnek.
 

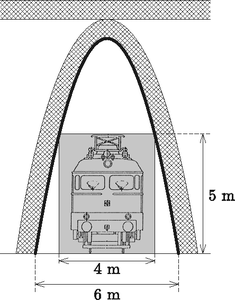
4. A vasúti szaknyelvben űrszelvénynek nevezik a szerelvények akadálytalan áthaladásához szükséges térnek a vágányokra merőleges keresztmetszetét. A nemzetközi szabványok szerint az űrszelvény jellemzően 4 m széles és 5 m magas. Az alakja általában követi a szerelvény alakját, de az egyszerűség kedvéért ez legyen most az ábrán szürkével jelzett téglalap. A vasút egy olyan híd alatt halad át, amelynek acél tartószerkezete parabolaív alakú. A tartószerkezet belső íve (az ábrán vastag fekete vonallal) a sínek szintjén 6 m széles és éppen nem lóg be az űrszelvénybe.
a) Milyen magas a híd tartószerkezete a belső ívének középső, legmagasabb pontján?   (8 pont)

A vasútvonal áthalad egy olyan 24 méter hosszú, egyenes alagúton is, amelynek keresztmetszete parabolaszelet alakú. A parabolaszeletet a koordináta-rendszerben megadott
y=-12x2+8
egyenletű parabola és az x tengely határolja. A koordináta-rendszerben 1 egység 1 métert jelent.
b) Hány m3 követ kellett kitermelni az alagút építése közben? Válaszunkat egészre kerekítve adjuk meg.  (6 pont)
 

 
Megoldás. a) Rögzítsünk úgy egy koordináta-rendszert, hogy az x-tengely a sínek szintje, az y-tengely pedig a parabolaív szimmetriatengelye legyen. Ekkor ennek a parabolának az általános egyenlete: y=-12px2+v.
Ebben a koordináta-rendszerben a parabolaív első síknegyedbe eső részén ki tudunk jelölni két pontot: A(3;0), és B(2;5). Az előbbi két pontot a parabola általános egyenletébe behelyettesítve megoldandó az alábbi egyenletrendszer:
0=-12p⋅32+v,5=-12p⋅22+v.
Ebből v=9 és p=0,5.
Mivel v éppen a keresett magasság, a tartószerkezet a belső ívének középső, legmagasabb pontján 9 méter magas.
b) A keresett térfogat a parabolaszelet területének és az alagút hosszának a szorzata. A parabola két zérushelye: x1=-4 és x2=4. A kiszámítandó T terület:
T=∫-44(-12x2+8)dx.
A határozott integrál értéke:
[-x36+8x]-44=(-646+32)-(646-32)=1283.
Tehát a kitermelt kő térfogata 1283⋅24=1024(m3).
 

II. rész
 

5. a) Határozzuk meg azt a legkisebb, különböző számjegyekből álló 6-jegyű természetes számot, amely a 0;1;2;3;4;5 számjegyekből áll és osztható 12-vel.  (5 pont)
b) A {0;1;2;3;4;5} halmaznak hány részhalmaza tartalmaz legalább 1 db páratlan számot?
  (3 pont)
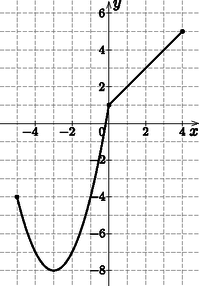
c) Adjuk meg az ábrán látható függvény hozzárendelési szabályát, és számítsuk ki a függvény E(-1;-4) pontjában húzott érintőjének meredekségét.  (8 pont)
 
 

 
Megoldás. a) Egy tízes számrendszerbeli szám pontosan akkor osztható 12-vel, ha osztható 3-mal és 4-gyel is. A képzett szám biztosan osztható 3-mal, mert a számjegyek összege (0+1+2+3+4+5=)15. A képzett szám csak akkor osztható 4-gyel, ha az utolsó két számjegye: 04; 12; 20; 24; 32; 40 vagy 52. A keresett szám akkor lesz a legkisebb, ha a nagy alaki értékű számjegyek kis helyiértéken állnak.
(Mivel a szám nem kezdődhet 0-val), a legkisebb feltételeknek megfelelő szám a 103 452.
 

b) A {0;1;2;3;4;5} halmaznak összesen 26=64 db részhalmaza van. Azok a részhalmazok, amelyek nem tartalmaznak páratlan számot, a {0;2;4} halmaz részhalmazai, melyek száma 23=8.
A kérdéses részhalmazok száma: 26-23=56.
 

c) Az ábrázolt függvény két részből áll: egy másodfokú és egy lineáris függvényből. A felfelé nyíló nem nyújtott parabola talppontja (és egyben a függvény minimuma) a (-3;-8) pont, így ha x∈[-5;0], akkor f(x)=(x+3)2-8. A lineáris függvény az y tengelyt a (0;1) pontban metszi, meredeksége 1, tehát ha x∈]0;4], akkor f(x)=x+1.
A függvény hozzárendelési szabálya:
f(x)={(x+3)2-8,ha  x∈[-5;0],x+1,ha  x∈]0;4].
Az E-ben húzott érintő meredekségét az f deriváltfüggvényének az x=-1 helyen felvett helyettesítési értéke adja meg: f'(x)=2x+6, f'(-1)=4.
 

 
6. Tekintsük az an=n2+2 sorozatot.
a) Határozzuk meg a limn→∞1an határértéket. Válaszunkat indokoljuk.  (2 pont) b) Számítsuk ki az (an) sorozat első száz tagjának összegét.  (4 pont) Az (an) sorozat egymást követő tagjai segítségével a bn=an+1-an sorozatot képeztük.
c) Igazoljuk, hogy a (bn) sorozat számtani sorozat.  (3 pont) d) Igazoljuk teljes indukcióval, hogy az (an) sorozat a1=3 és n>1 esetén megadható az
an=(1+2n-1n2-2n+3)⋅an-1
rekurzióval is.  (7 pont)
 
Megoldás. a) Ha n→∞, akkor n2+2 is végtelenbe tart. (Mivel a tört nevezője végtelenbe tart), ezért
limn→∞1n2+2=0.

b) A sorozat első száz tagját összeadva:
a1+a2+...+a100=(12+2)+(22+2)+...+(1002+2)=
a jobb oldalon lévő összeg tagjait csoportosítva:
=(12+22+...+1002)+2⋅100.
A zárójelben az első 100 db pozitív egész szám négyzetének összege (n(n+1)(2n+1)6) szerepel, ezért a sorozat első száz tagjának összege:
100(100+1)(2⋅100+1)6+2⋅100=338550.
 

c) Azt kell megmutatni, hogy a (bn) sorozat egymást követő tagjainak különbsége állandó. A sorozat képzési szabályába behelyettesítve:
bn=an+1-an=[(n+1)2+2]-[(n2+2)]=2n+1,bn-bn-1=(2n+1)-(2n-2+1)=2,
tehát a sorozat valóban számtani.
 

d) Teljes indukciót alkalmazunk. Ha n=1, akkor az állítás igaz, mert mindkét képzési szabályból a1=3.
Tegyük fel, hogy az állítás igaz egy k pozitív egész számra, azaz létezik olyan k szám, amelyre teljesül, hogy ak-1=(k-1)2+2. Ekkor igazolnunk kell, hogy:
ak=(1+2k-1k2-2k+3)⋅ak-1=k2+2.
Az indukciós feltevés miatt:
ak=(1+2k-1k2-2k+3)⋅((k-1)2+2)==(1+2k-1k2-2k+3)⋅(k2-2k+3)==k2-2k+3+2k-1==k2+2.
 

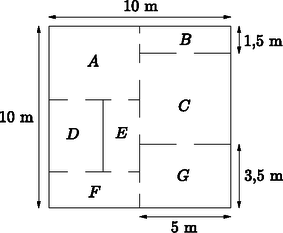
7. Az ábrán egy családi ház földszintjének alaprajza látható a benne lévő hét helyiséggel és az ajtókkal együtt. A rajzon feltüntettük a földszint és néhány helyiség méretét is. (A földszinti bejárati ajtó nem szerepel az ábrán, mert a megoldáshoz az nem szükséges.)

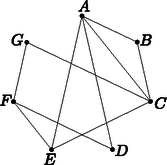
a) A házban lévő helyiségeket és az ajtókat egy gráffal szemléltethetjük úgy, hogy a gráf csúcsai (A,B,C,D,E,F,G) a helyiségeket jelölik, a gráf két csúcsa között pedig pontosan akkor vezet él,
ha a két csúcsnak megfelelő helyiség között van ajtó. Rajzoljuk fel a családi ház földszintjének gráfját (a csúcsok azonosításával együtt), és határozzuk meg a felrajzolt gráfban a fokszámok összegét.  (3 pont)
A lakás fölött a földszinttel megegyező méretű padlás, a ház alapterületének negyede alatt pince is van. A család macskája a pince padlóján fele olyan szívesen, a padláson viszont kétszer olyan szívesen van, mint a földszinten.
b) Mekkora valószínűséggel fekszik a macska a C jelű szobában?  (8 pont)
c) Legalább hány élt kell kitörölni egy 7 csúcsú teljes gráfból ahhoz, hogy az már ne legyen összefüggő? Állításunkat igazoljuk.  (5 pont)
 
Megoldás. a) A családi ház földszintjének gráfja:
A fokszámok összege: 2⋅4+2⋅3+3⋅2=20.
 
 

b) I. megoldás. A földszint és a padlás alapterülete is 100 m2, a pince alapterülete 25 m2. Ezek összege 225 m2.
Ha a macska a földszinten van, akkor a valószínűség 100225⋅p, ha a padláson, akkor 100225⋅2p, ha a pincében, akkor 25225⋅p2. A kedvező esetek száma: 100225⋅p. Az összes eset száma:
100225⋅p+100225⋅2p+25225⋅p2.
Annak a valószínűsége, hogy a macska a földszinten van:
P=100225⋅p100225⋅p+100225⋅2p+25225⋅p2=0,32.
Mivel a C jelű szoba alapterülete 25 m2, a földszint alapterülete 100 m2, így az ott tartózkodás valószínűsége: 25100⋅0,32=0,08.
 

II. megoldás. Jelölje p annak a valószínűségét, hogy a macska a földszinten tartózkodik. Ez esetben annak a valószínűsége, hogy a padláson van 2p, annak a valószínűsége, hogy a pincében fekszik p8. Mivel a macska vagy a pincében, vagy a földszinten vagy a padláson tartózkodik, ezért az egyes helyeken való tartózkodások valószínűségeinek összege biztosan 1:
p8+p+2p=1,ebbőlp=825.
Mivel a C jelű szoba alapterülete 25 m2, a földszint alapterülete 100 m2, így az ott tartózkodás valószínűsége: 25100⋅0,32=0,08.
 

c) I. megoldás. Ha arra törekszünk, hogy egy 7 csúcsú teljes gráfból a lehető legkevesebb élt töröljük ki, akkor az úgy teljesülhet, ha csak 2 részgráfra, ‐ amelyek teljes gráfok ‐, szakítjuk szét az eredeti gráfot. Ez egy 7 csúcsú teljes gráf esetén háromféleképpen jöhet létre: ha az eredeti gráfot egy 3 és 4 csúcsú teljes gráfra szakítjuk szét, akkor a két gráf éleinek száma összesen 9.
Ha az eredeti gráfot egy 2 és 5 csúcsú teljes gráfra szakítjuk szét, akkor a két gráf éleinek száma összesen 11.
Ha az eredeti gráfot egy 1 és 6 csúcsú teljes gráfra szakítjuk szét, akkor a két gráf éleinek száma összesen 15.
Így az eredeti gráfból legalább 21-15=6 db élt kell kitörölni, hogy ne legyen összefüggő.
 

II. megoldás. Ha arra törekszünk, hogy egy 7 csúcsú teljes gráfból a lehető legkevesebb élt töröljük ki, akkor az úgy teljesülhet, ha csak 2 részgráfra, ‐ amelyek teljes gráfok ‐, szakítjuk szét az eredeti gráfot.
Jelölje az egyik részgráfban lévő csúcsok számát x, ekkor a másik részgráfban 7-x csúcs lesz, így az egyes részgráfok éleinek száma:
x⋅(x-1)2és(7-x)⋅(6-x)2.
A megmaradó élek száma x függvényében:
e(x)=x⋅(x-1)2+(7-x)⋅(6-x)2=x2-7x+21.
Mivel x∈{1;2;3;4;5;6}, ezért az e függvény akkor maximális, ha x=1 vagy x=6 (azaz ha egyetlen izolált pont keletkezik).
Így az eredeti gráfból legalább 6 db élt kell kitörölni, hogy ne legyen összefüggő.
 

III. megoldás. Ha arra törekszünk, hogy egy 7 csúcsú teljes gráfból a lehető legkevesebb élt töröljük ki, akkor az úgy teljesülhet, ha csak 2 részgráfra, ‐ amelyek teljes gráfok ‐, szakítjuk szét az eredeti gráfot.
Jelölje az egyik részgráfban lévő csúcsok számát x, ekkor a másik részgráfban 7-x csúcs lesz. Mivel minden csúcs minden csúccsal össze van kötve a teljes gráfban, ezért az x csúcsú részgráf mindegyik csúcsából a másik részgráfba vezető mindegyik élt ki kell törölni, ezért a kitörlendő élek száma x függvényében
k(x)=-x2+7x.
Mivel x∈{1;2;3;4;5;6}, ezért az k függvény akkor minimális, ha x=1 vagy x=6 (azaz ha egyetlen izolált pont keletkezik).
Így az eredeti gráfból legalább 6 db élt kell kitörölni, hogy ne legyen összefüggő.
 

 
8. Az alábbi táblázat hazánk napsütéses óráinak átlagos mennyiségét mutatja órában mérve az egyes évszakokban.
 
Tavasz  Nyár  Ősz  Tél  575,2  845,7  403  180,1  
 

a) Határozzuk meg a napsütéses órák mennyiségének átlagát és szórását.
 
 (4 pont)
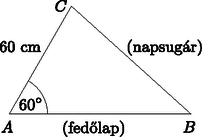
Az ábrán látható napóra egy magyar városban található. A napóra mutatójának hossza 60 cm, északi irányba áll és a vízszintes talapzattal 60∘-os szöget zár be. A tavaszi nap-éj egyenlőség idején (2018. március 20-án) a Nap delelési magassága 42∘ volt. A Nap delelési magasságán a Nap irányába mutató félegyenesnek a vízszintessel bezárt szögét értjük.
 
 

b) Milyen hosszú volt ekkor a napóra mutatójának árnyéka a vízszintes alaplapon?  (5 pont)
A napóra felületének koszolódását úgy szeretnék csökkenteni, hogy talapzatra helyezik a napórát. A talapzat egy olyan téglatest alakú betontömb, amelynek fedőlapját és oldallapjait 2 cm vastag márványlappal borítják be. A márvánnyal beborított betontömb alaplapja 1 m oldalhosszúságú négyzet, magassága 80 cm. A márványbevonat készítése közben a megvásárolt mennyiség 10%-a hulladék lesz.
c) Mennyibe kerül a betontömb beborításához szükséges márvány, ha 1 m3 2 cm vastag márványlap ára 540 000 Ft? Válaszunkat tízezer forintra kerekítve adjuk meg.  (7 pont)
 
Megoldás. a) A napsütéses órák átlaga:
x¯=575,2+845,7+403+180,14=501  (óra).
A napsütéses órák szórása:
σ=(-74,2)2+344,72+(-98)2+(-320,9)24≈243,36  (óra).
 

b) A feladat megértését tükröző ábra:
 
 

Az ABC∢=β=42∘, így a háromszög C csúcsánál lévő γ szöge 78∘. Az ABC háromszögben a szinusztétel alapján:
sin78∘sin42∘=AB60,
ahonnan AB≈87,71 cm.
 

c) I. megoldás. A betonnal kiöntésre kerülő test egy négyzet alapú hasáb, melynek alapéle 0,96 m, magassága 0,78 m. A betonnal kiöntött rész térfogata:
Vb=0,96⋅0,96⋅0,78(≈0,72m3).
A talapzat térfogata:
Vt=1⋅1⋅0,8(=0,8m3).
A talapzatba beépítésre kerülő márvány térfogata:
Vm=Vt-Vb≈0,08m3.
Mivel a vásárolt mennyiség 10%-a hulladék lesz, ezért a beépítésre kerülő térfogat a vásárolt mennyiség 90%-a, ezért a vásárolt márvány térfogata:
V=10090⋅Vm≈0,09m3.
A márványborítás ára kb. 50 000 Ft.
 

II. megoldás. A márványborítás területét megkapjuk, ha a fedőlap területéhez hozzáadjuk a két-két egyforma oldallap területét. A fedőlap élei 1 méter hosszúak, az egyik oldallap élei 1 m és 0,78 m, a szomszédos oldallap élei 0,96 m és 0,78 m hosszúságúak.
A=1⋅1+2⋅1⋅0,78+2⋅0,96⋅0,78≈4,06m2.
(A márványlapok térfogata:)
V≈4,06⋅0,02≈0,08m3.
Mivel a vásárolt mennyiség 10%-a hulladék lesz, ezért a beépítésre kerülő térfogat a vásárolt mennyiség 90%-a, ezért a vásárolt márvány térfogata:
V=10090⋅Vm≈0,09m3.
A márványborítás ára kb. 50 000 Ft.
 

 
9. Az alábbi táblázatban a gyorshajtás miatt bekövetkezett halálos közúti balesetek száma látható a Nyugat-Dunántúlon 2010-től 2018-ig a megadott időszakban.
 

Halálos közúti balesetek száma 2010-től 2018-ig 01.01-től 02.28-ig (Nyugat-Dunántúl)
 

Év  2010  2011  2012  2013  2014  2015  2016  2017  2018  Balesetek száma  9  8  12  7  18  14  15  12  8  
 

a) Határozzuk meg a balesetek számának mediánját és terjedelmét.  (3 pont)
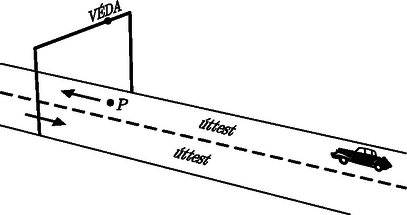
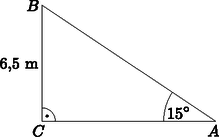
Hazánkban a rendőrség rendszámtábla alapján azonosítja a gyorshajtókat. Egy sebességmérés alkalmával az úttesten szabályosan közlekedő autós éppen szemben van a mérést végző készülékkel, amit VÉDÁ-nak hívnak. A 6,5 m magas állványra szerelt sebességmérő berendezésből 15∘-os lehajlási szögben érkezik az úttestre a lézernyaláb.
(A lézernyaláb szélességétől az egyszerűség kedvéért most tekintsünk el.)
 

b) Érzékeli-e a sebességmérő berendezés az ebben a pillanatban a P ponttól 40 m távolságban az úttest közepén a VÉDA irányába közlekedő személyautót?
  (4 pont)
Egy biztosító honlapján a következőket olvashatjuk:
,,Az autóbiztosítással rendelkező ügyfeleink 65 százalékát férfiak, 35 százalékát nők teszik ki. Balesetek szempontjából a férfiak a károkozók 69 százalékát teszik ki. Úgy tűnik, a hölgyek biztonságosabban vezetnek, ugyanis a károkozók körében csak 31 százalékos az arányuk.''
c) Vizsgáljuk meg, hogy (a leírtak alapján) az alábbi két esemény közül melyiknek nagyobb a valószínűsége.  (9 pont)
I. Ha hölgy vezeti az autót, akkor ő okozza a balesetet.
II. Ha férfi vezeti az autót, akkor ő okozza a balesetet.
 
Megoldás. a) A medián: 12, a terjedelem: 11.
 

b) Készítsünk ábrát.

Az ABC derékszögű háromszögben:
tg15∘=6,5AC, ahonnan AC=6,5tg15∘≈24,26m.
Tehát a sebességmérő berendezés 40 m távolságból nem érzékeli a személyautót.
 

c) Jelölje A azt az eseményt, hogy a biztosított ügyfél férfi, B azt, hogy nő, C pedig azt, hogy baleset történik. Ekkor a feladat szövege alapján: P(A)=0,65; P(B)=0,35 és P(C)=p.
Annak a valószínűsége, hogy ha baleset történik, akkor azt nő okozza:
P(B|C)=0,31.
Annak a valószínűsége, hogy ha baleset történik, akkor azt férfi okozza: P(A|C)=0,69.
(A feltételes valószínűség definíciója alapján:)
P(B|C)=P(BC)P(C)ésP(A|C)=P(AC)P(C),
ahonnan P(BC)=0,31p és P(AC)=0,69p.
 

Annak a valószínűsége, hogy ha nő vezeti az autót, akkor ő okozza a balesetet:
P(C|B)=0,31p0,35≈0,89p.
Annak a valószínűsége, hogy ha férfi vezeti az autót, akkor ő okozza a balesetet:
P(C|A)=0,69p0,65≈1,06p.
Mivel P(C|B)<P(C|A), így a II. esemény bekövetkezésének valószínűsége nagyobb.