A nyílt kulcsú titkosító algoritmus matematikai alapjait 1976-ban fektette le Ron Rivest, Adi Shamir és Len Adleman. A nevük kezdőbetűi alapján elnevezett RSA algoritmus napjaink egyik leggyakrabban használt adattitkosító eljárása. A szakirodalomban elérhető matematikai alapok felhasználásával magam is elkészítettem a titkosító eljárás ‐ gyakorlatban is jól használható ‐ programját. A kulcsgenerálás algoritmusának pontosabb vizsgálatával sikerült kimutatni, hogy a prímek mellett speciális összetett számok is kiválóan alkalmazhatók kulcsok generálásához, sőt jelentősen csökkenthetik a kulcsok előállításának időtartamát.
A dolgozat megmutatja, hogy a Fermat féle prímteszt ‐ annak ellenére, hogy prímek keresésére nem megbízható, mert átbújhatnak rajta összetett számok is ‐ tökéletesen alkalmas megbízható RSA kulcsok generálására.
A továbbiakban összefoglaljuk azokat a matematikai tételeket, algoritmusokat, melyek az eljárás elvi alapjait adják.

 

Bizonyítás. Az $a\mathrm{,2}a\mathrm{,}\text{...}\mathrm{,}\left(p-1\right)a$ számokat osszuk el $p$-vel és a maradékok legyenek $m_1\mathrm{,}{m}_2\mathrm{,}\text{...}\mathrm{,}{m}_{p-1}$, azaz:

${\displaystyle \begin{array}{ccc}\hfill {\displaystyle a}& {\displaystyle =}\hfill & {\displaystyle k_{1}p+m_1\mathrm{,}}\hfill \\ \hfill {\displaystyle 2a}& {\displaystyle =}\hfill & {\displaystyle k_{2}p+m_2\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle ⋮}\hfill & {\displaystyle }\hfill \\ \hfill {\displaystyle \left(p-1\right)a}& {\displaystyle =}\hfill & {\displaystyle k_{p-1}p+m_{p-1}\mathrm{.}}\hfill \end{array}}$

A maradékok között nem lehet két egyenlő, mert ha $m_i=m_j$ lenne, akkor $\left(i-j\right)a$ osztható lenne $p$-vel, de ez lehetetlen, mert sem $\left(i-j\right)$, sem $a$ nem osztható $p$-vel.
A fenti egyenlőségek oldalait összeszorozva $\left(p-1\right)!a^{p-1}=Kp+\left(p-1\right)!$ , hiszen a jobb oldalon megjelenik a $p-1$ darab különböző maradék szorzataként $\left(p-1\right)!$ . Ebből átrendezéssel következik, hogy $\left(p-1\right)!\left(a^{p-1}-1\right)=Kp$. Mivel $\left(p-1\right)!$ nem osztható $p$-vel, azért $a^{p-1}-1$ osztható $p$-vel, azaz $a^{p-1}\equiv 1\left(\text{mod}p\right)$.

 

Definíció. Legyen $\phi \left(n\right)$ az $n$-nél nem nagyobb, nemnegatív, $n$-hez relatív prím számok darabszáma ‐ ez az Euler-féle $\phi$ függvény.

 

Tétel. Ha $A$ és $N$ relatív prímek, akkor $A^{\phi \left(N\right)}\equiv 1\left(\text{mod}N\right)$ (Euler tétele ‐ a kis Fermat-tétel Euler-féle általánosítása).
A bizonyítás lényegében ugyanaz, mint a kis Fermat-tétel esetében: Legyenek $m_1\mathrm{,}{m}_2\mathrm{,}\text{...}\mathrm{,}{m}_{\phi \left(N\right)}$ az $N$-hez relatív prím osztási maradékok, és ezek $A$-szorosainak is tekintsük az $N$-nel való osztásnál keletkező maradékait:

${\displaystyle \begin{array}{ccc}\hfill {\displaystyle A{m}_1}& {\displaystyle \equiv }\hfill & {\displaystyle s_1\left(\text{mod}N\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle A{m}_2}& {\displaystyle \equiv }\hfill & {\displaystyle s_2\left(\text{mod}N\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle ⋮}\hfill & {\displaystyle }\hfill \\ \hfill {\displaystyle A{m}_{\phi \left(N\right)}}& {\displaystyle \equiv }\hfill & {\displaystyle s_{\phi \left(N\right)}\left(\text{mod}N\right)\mathrm{.}}\hfill \end{array}}$

Könnyen belátható, hogy az $s_1\mathrm{,}{s}_2\mathrm{,}\text{...}\mathrm{,}{s}_{\phi \left(N\right)}$ számok az $m_1\mathrm{,}{m}_2\mathrm{,}\text{...}\mathrm{,}{m}_{\phi \left(N\right)}$ számok egy permutációja. Ehhez elegendő megmutatni, hogy az $s_i$ számok relatív prímek $N$-hez, és nincs közöttük két egyenlő. Ha $\left(s_i\mathrm{,}N\right)=p>1$ lenne, akkor $A{m}_i$ is osztható lenne $p$-vel, ami lehetetlen. Ha lenne köztük két egyenlő, akkor
$A\left(m_i-m_j\right)=A{m}_i-A{m}_j$ osztható lenne $N$-nel, ami szintén lehetetlen, mert $\left(A\mathrm{,}N\right)=1$ és $|m_i-m_j|<N$. A fenti kongruenciák szorzatából ‐ a maradékok szorzatával való egyszerűsítés után ‐ következik az állítás.
Ha $N$ prím, akkor $\phi \left(N\right)=N-1$, így belátható, hogy Euler tétele valóban a kis Fermat-tétel általánosítása.
Megemlítjük még a $\phi$ függvény néhány ‐ későbbiekben felhasznált ‐ alapvető tulajdonságát:

 

Tétel. Ha $p$ és $q$ relatív prímek, akkor $\phi \left(pq\right)=\phi \left(p\right)\phi \left(q\right)$.
Speciálisan, ha $p$ és $q$ egymástól különböző prímek, akkor $\phi \left(pq\right)=\phi \left(p\right)\phi \left(q\right)=\left(p-1\right)\left(q-1\right)$.

 

Tétel. Tetszőleges $n\ge 1$ és $p$ prím esetén $\phi \left(p^n\right)=\left(p-1\right)p^{n-1}$.

 

Bizonyítás. Mivel $p$ prím, azért az $\mathrm{1,2,3,}\text{...}\mathrm{,}{p}^n$ számok között $p$-vel csak a $p\mathrm{,2}p\mathrm{,3}p\mathrm{,}\text{...}\mathrm{,}{p}^{n-1}\cdot p=p^n$ számok oszthatók, a többi relatív prím $p^n$-hez. A $p$-vel oszthatók száma $p^{n-1}$, tehát a fenti intervallum $p^n$-hez relatív prímjeinek száma $p^n-p^{n-1}=p^{n-1}\left(p-1\right)$.

 

Tétel. Legyen $n$ prímtényezős alakja

$\begin{array}{c}{\displaystyle n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\text{...}{p}_r^{{\alpha }_r}=\prod _{i=1}^r{p}_i^{{\alpha }_i}\mathrm{,}\text{ahol}{\alpha }_i>0.}\end{array}$

Ekkor $\phi \left(n\right)$ felírható a következő szorzat alakjában:

$$\begin{gathered} \begin{array}{c}{\displaystyle \phi \left(n\right)=\prod _{i=1}^r{p}_i^{{\alpha }_i-1}\left(p_i-1\right)=n\prod _{i=1}^r\left(1-\frac{1}{p_i}\right)=n\prod _{p\mid n \\ p\text{ <span style="font-weight: normal;font-style: normal;">prím</span>}}^{}\left(1-\frac{1}{p}\right)\mathrm{.}}\end{array} \end{gathered}$$

 

2. Az $\text{<span style="font-weight: bold;"><span style="font-style: italic;">a</span></span>}x+by=1$ diophantoszi egyenlet megoldhatósága és
a modális inverz fogalma

 

Tétel. Legyenek $a$ és $b$ egész számok. Az $ax+by=1$ diophantoszi egyenletnek akkor és csak akkor van egészekből álló $x$, $y$ megoldása, ha $a$ és $b$ relatív prímek, azaz $\left(a\mathrm{,}b\right)=1$.
$a)$ Ha $a$ és $b$ legnagyobb közös osztójára $\left(a\mathrm{,}b\right)>1$, akkor az egyenlet átírható $\left(a\mathrm{,}b\right)\left(a_{1}x+b_{1}y\right)=1$ alakba.
Semmilyen $x$, $y$ pár nem elégítheti ki az előbbi egyenletet, mert a jobb oldalon álló 1 nem osztható $\left(a\mathrm{,}b\right)$-vel.
$b)$ Legyen $\left(a\mathrm{,}b\right)=1$. Az általánosság csorbítása nélkül feltehető, hogy $a$ és $b$ pozitív. Átrendezés után $x=\frac{1-by}{a}$, azaz keresni kell azt az $y$ egész számot, amelyre $by$-nak az $a$-val való osztási maradéka 1; megmutatjuk, hogy létezik ilyen $y$ szám. A $b$ számot szorozzuk meg az $\mathrm{1,2,}\text{...}\mathrm{,}a$ számokkal, és képezzük az $a$-val való osztás maradékait:

${\displaystyle \begin{array}{ccc}\hfill {\displaystyle 1b}& {\displaystyle =}\hfill & {\displaystyle k_{1}a+m_1\mathrm{,}}\hfill \\ \hfill {\displaystyle 2b}& {\displaystyle =}\hfill & {\displaystyle k_{2}a+m_2\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle ⋮}\hfill & {\displaystyle }\hfill \\ \hfill {\displaystyle ab}& {\displaystyle =}\hfill & {\displaystyle k_{a}a+m_a\left(m_a=0\right)\mathrm{.}}\hfill \end{array}}$

Belátható, hogy az $m_1\mathrm{,}{m}_2\mathrm{,}\text{...}\mathrm{,}{m}_a$ maradékok a $\mathrm{0,1,2,}\text{...}\mathrm{,}a-1$ számok egy permutációja, tehát elő kell fordulnia 1-nek is mint osztási maradéknak. Indirekte tegyük fel ugyanis, hogy van köztük két egyenlő, például $m_i=m_j$, ekkor $\left(i-j\right)b=\left(k_i-k_j\right)a\left(\ne 0\right)$. Mivel $|i-j|<a$, azért $i-j$ nem lehet osztható $a$-val, de akkor ‐ $\left(a\mathrm{,}b\right)=1$ miatt ‐ $\left(i-j\right)b$ sem.

 

1. következmény. Az $ax+by=c$ diophantoszi egyenletnek mindig van megoldása, ha $\left(a\mathrm{,}b\right)=1$. (Ugyanis, ha $x_0$ és $y_0$ megoldása $ax+by=1$-nek, akkor $c{x}_0$ és $c{y}_0$ megoldása $ax+by=c$-nek.)

 

2. következmény. Az $ax+by=\left(a\mathrm{,}b\right)$ diophantoszi egyenletnek mindig van megoldása. Ez eredetileg Bézout lemmája. A megoldás nem egyértelmű, mert ha $x$ és $y$ megoldás, akkor $x_1=x+kb$ és $y_1=y-ka$ is az. Az $a\mathrm{,}b$ számok legnagyobb közös osztóját, illetve az egyenlet egy $x$, $y$ megoldását a kiterjesztett euklideszi algoritmussal lehet meghatározni (lásd ott).

 

Az $ax+by=1$ alakú diophantoszi egyenletek szoros kapcsolatban vannak az $ax\equiv 1\left(\text{mod}n\right)$ alakú kongruenciákkal. Formális okok miatt az $ax\equiv 1\left(\text{mod}n\right)$ kongruencia $x$ megoldását tekinthetjük az $a$ szám modális multiplikatív inverzének, azaz jelölhetjük így is: $x\equiv a^{-1}\left(\text{mod}n\right)$. Természetesen ha $x_0$ megoldás, akkor $x_0+kn$ is az ($k$ tetszőleges egész szám lehet).

 

Tétel. Az $ax\equiv 1\left(\text{mod}n\right)$ kongruenciának akkor és csak akkor van x megoldása, ha $\left(a\mathrm{,}n\right)=1$. $($Ha van megoldás, akkor szimmetria okok miatt $\left(x\mathrm{,}n\right)=1.)$

 

Bizonyítás. Tekintsük az $ax+ny=1$ diophantoszi egyenletet. Ennek akkor és csak akkor van megoldása, ha $\left(a\mathrm{,}n\right)=1$. Másrészt, az $ax=1-ny$ alakból látszik, hogy az egyenlet éppen azt jelenti, hogy $ax\equiv 1\left(\text{mod}n\right)$.

 

Következmény. Az Euler‐Fermat-tételt felhasználva, ha $\left(a\mathrm{,}n\right)=1$, akkor az $ax\equiv 1\left(\text{mod}n\right)$ kongruencia megoldása felírható $x\equiv a^{\phi \left(n\right)-1}\left(\text{mod}n\right)$ alakban is. Ez az alak többnyire csak elméleti jelentőségű, mivel konkrét esetekben a modális inverz meghatározásához a kiterjesztett euklideszi algoritmust használjuk; ez eldönti, hogy az $\left(a\mathrm{,}n\right)=1$ feltétel teljesül-e, s ha igen, akkor egyidejűleg megadja az inverzet is.

 

 

3. A rend és a primitív gyök fogalma

Képezzük $g$ egymás utáni ($\mathrm{1.,2.,}\text{...}\mathrm{,}k$-adik) hatványait $\left(\text{mod}p\right)$. Ha az így képzett számok között megjelenik a 0, akkor minden további szám már 0 marad. Ha nem jelenik meg a 0, akkor előbb-utóbb ciklusba esik, azaz létezik egy legkisebb $k>1$ egész, amelyre $g\equiv g^k\left(\text{mod}p\right)$ lesz. Ekkor a ciklus hossza $k-1$. (Vegyük észre, hogy ha $\left(g\mathrm{,}p\right)=1$, akkor 0 nem jelenik meg.)
Ha a tetszőlegesen választott $g$ és $p$ esetében létrejön a fenti típusú ciklus, akkor definíció szerint a ciklus hossza $g$ rendje $\left(\text{mod}p\right)$ ‐ melynek jelölése $o_p\left(g\right)$ (kiejtve ordo $g\left(\text{mod}p\right)$).
Könnyen belátható, hogy ha $\left(g\mathrm{,}p\right)=1$ akkor $o_p\left(g\right)$ mindig létezik, és az Euler‐Fermat-tétel miatt $o_p\left(g\right)\le \phi \left(p\right)$. Sőt, az is belátható, hogy ha $g^k\equiv 1\left(\text{mod}p\right)$, akkor a ciklikusság miatt $o_p\left(g\right)$ osztja $k$-t, speciálisan $o_p\left(g\right)-\phi \left(p\right)$ is mindig fennáll.
Ha $\left(g\mathrm{,}p\right)=1$ és $o_p\left(g\right)=\phi \left(p\right)$, akkor $g$-t $p$ primitív gyöknek nevezzük $\left(\text{mod}p\right)$. Ha $g$ primitív gyök $\left(\text{mod}p\right)$, akkor a $g^1\mathrm{,}{g}^2\mathrm{,}\text{...}\mathrm{,}{g}^{\phi \left(p\right)}\equiv 1$ számok $\left(\text{mod}p\right)$ maradékai a $p$-hez relatív prím maradékok egy permutációját adják.
Most megmutatjuk, hogy a $\left(g\mathrm{,}p\right)=1$ nem csak elégséges, de szükséges feltétel is $o_p\left(g\right)$ létezésére, így arra is, hogy $g$ primitív gyök legyen $\left(\text{mod}p\right)$. Ennek belátásához csupán azt kell észrevennünk, hogy $a\equiv b\left(\text{mod}m\right)$ esetén $\left(a\mathrm{,}m\right)=\left(b\mathrm{,}m\right)$. Ha létezik $o_p\left(g\right)$, akkor van olyan $k>0$ egész szám, amelyre $g^k\equiv 1\left(\text{mod}p\right)$, így $\left(g^k\mathrm{,}p\right)=\left(\mathrm{1,}p\right)=1$, ezért $\left(g\mathrm{,}p\right)=1$-nek is teljesülnie kell.
Bizonyítás nélkül közöljük a primitív gyök létezésére vonatkozó alábbi tételt:

 

Primitív gyök pontosan (csak) az $N=\mathrm{2,4,}{p}^k\mathrm{,2}{p}^k$ alakú modulusokra létezik, ahol $p$ páratlan prímszám és $k>0$ egész.

 

 

4. A kiterjesztett euklideszi algoritmus

Két szám legnagyobb közös osztójának meghatározására ‐ nagy számok esetében ‐ a prímtényezős felbontásra alapozott eljárás időben kivárhatatlan.
Az $a$, $b$ számok legnagyobb közös osztóját (LNKO) a közismert euklideszi algoritmussal lehet hatékonyan meghatározni. Az eljárás kiterjesztésével (veremtechnika alkalmazásával) az $ax+by=\left(a\mathrm{,}b\right)$ egyenlet $x$, $y$ megoldását és az $ax\equiv 1\left(\text{mod}n\right)$ kongruenciából az $x\left(\text{mod}n\right)$ inverzét is gyorsan kiszámíthatjuk.
Legyen $M_0$ és $M_1$ két pozitív egész szám, melyekből sorozatos maradékos osztásokkal képezzük a következő nemnegatív egészeket:

${\displaystyle \begin{array}{ccc}\hfill {\displaystyle M_0}& {\displaystyle =}\hfill & {\displaystyle k_0{M}_1+M_2\left(M_2<M_0\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle M_1}& {\displaystyle =}\hfill & {\displaystyle k_1{M}_2+M_3\left(M_3<M_1\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle M_2}& {\displaystyle =}\hfill & {\displaystyle k_2{M}_3+M_4\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle ⋮}\hfill & {\displaystyle }\hfill \\ \hfill {\displaystyle M_n}& {\displaystyle =}\hfill & {\displaystyle k_n{M}_{n+1}+0.}\hfill \end{array}}$

Mivel az $M_2\mathrm{,}{M}_3\mathrm{,}\text{...}$ folyamatosan csökkennek (a páros indexűek monoton csökkenek $M_0$-tól, míg a páratlan indexűek $M_1$-től lefelé), ezért az $n+1$ osztás után a maradék 0 lesz.
Az $M_{n+1}$ értéke $\left(a\mathrm{,}b\right)$, azaz az LNKO. Az, hogy $M_{n+1}$ a kiinduló két ($M_0$ és $M_1$) szám közös osztója, következik az algoritmusból, a hátulról induló sorozatos visszahelyettesítésekből. Azt, hogy $M_{n+1}$ a kiinduló két ($M_0$ és $M_1$) szám legnagyobb közös osztója a következő módon láthatjuk be: Legyen $P$ az $M_0$ és $M_1$ számok egyik közös osztója. Az algoritmusból következik, hogy $P$ osztója $M_2$-nek is, illetve tovább folytatva a gondolatmenetet valamennyi $M_i$-nek, beleértve $M_{n+1}$-et is. Tehát $M_{n+1}$-et osztja valamennyi $P$ közös osztó, ezért $M_{n+1}$ a legnagyobb közös osztó.
A fenti algoritmus hátulról visszafelé alkalmazva, lehetővé teszi az $ax+by=\left(a\mathrm{,}b\right)$ egyenlet $x$, $y$ megoldásainak meghatározását is (ez az algoritmus kiterjesztése).
Foglaljuk táblázatba a fenti algoritmus egy-egy sorának számait ($A$, $B$, $R$, $K$) az alábbiak szerint: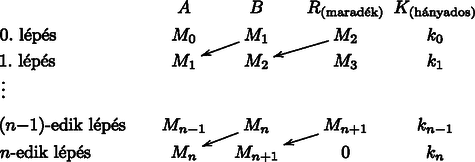

 

 

 

Az $A$, $B$, $R$, $K$ oszlopok számait ‐ az $i$-edik sorban ‐ jelöljük $a_i\m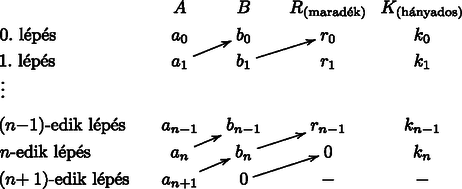athrm{,}{b}_i\mathrm{,}{r}_i\mathrm{,}{k}_i$-vel.

 

 

 

Vegyük észre, hogy minden sorban az $\left(a_i\mathrm{,}{b}_i\right)=a_{n+1}\left(=\text{LNKO}\right)$ azonosak minden $i=\mathrm{0,}\text{...}\mathrm{,}n+1$ esetén. (Az $\left(n+1\right)$-edik sort az egységes jelölés végett szúrtuk csak be.)
Az $ax+by=1$ diophantoszi egyenlet vizsgálatánál említett 2. következmény (Bézout-lemma) miatt minden sorra igaz, hogy az $\left(a_i\mathrm{,}{b}_i\right)=a_i{x}_i+b_i{y}_i$ egyenletnek van $x_i$, $y_i$ megoldása. Speciálisan az $\left(n+1\right)$-edik sornál $x_{n+1}=1$, $y_{n+1}=0$.
Megmutatjuk, hogy az $i$-edik sor $x_i$, $y_i$ együtthatói származtathatók az $\left(i+1\right)$-edik sor együtthatóiból, azaz hátulról visszafelé indulva az $x_{n+1}\mathrm{,}{y}_{n+1}=\mathrm{1,0}$ párból kiszámítható az $x_0$, $y_0$ pár, azaz meghatározható az $\left(a\mathrm{,}b\right)=ax+by$ diophantoszi egyenlet megoldása.
Tegyük fel, hogy az $\left(a_{i+1}\mathrm{,}{b}_{i+1}\right)=a_{i+1}{x}_{i+1}+b_{i+1}{y}_{i+1}$ egyenlet $x_{i+1}$, $y_{i+1}$ megoldása már ismert. Ugyanezt az összefüggést az $i$-edik sorra alkalmazva $\left(a_i\mathrm{,}{b}_i\right)=a_i{x}_i+b_i{y}_i$. Behelyettesítve a felfelé mutató nyilakkal jelölt egyenlőségeket, valamint felhasználva a sor elemei közötti belső összefüggést:

${\displaystyle \begin{array}{cc}\hfill {\displaystyle \left(a_i\mathrm{,}{b}_i\right)}& {\displaystyle =a_i{x}_i+b_i{y}_i=\left(k_i{b}_i+r_i\right)x_i+b_i{y}_i=\left(k_i{a}_{i+1}+b_{i+1}\right)x_i+a_{i+1}{y}_i=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =a_{i+1}\left(k_i{x}_i+y_i\right)+b_{i+1}{x}_i=\left(a_{i+1}\mathrm{,}{b}_{i+1}\right)\mathrm{.}}\hfill \end{array}}$

Az együtthatók egyenlőségéből $x_{i+1}=k_i{x}_i+y_i$ és $y_{i+1}=x_i$, ahonnan átrendezéssel:

${\displaystyle \begin{array}{cc}\hfill {\displaystyle x_i}& {\displaystyle =y_{i+1}\mathrm{,}}\hfill \\ \hfill {\displaystyle y_i}& {\displaystyle =x_{i+1}-k_i{x}_i=x_{i+1}-k_i{y}_{i+1}\mathrm{,}}\hfill \end{array}}$

vagyis az $i$-edik sor együtthatói kiszámíthatók az $\left(i+1\right)$-edik sor együtthatóiból, tehát az eljárás végén megkapjuk a keresett $x_0$, $y_0$ megoldást.
Vegyük észre, hogy az algoritmus alkalmazásakor szükségünk van a $k_i$ hányadosokra, melyeket az LNKO meghatározásakor veremben kell elhelyezni. Mivel az $ax\equiv 1\left(\text{mod}n\right)$ kongruencia megoldása ekvivalens az $ax-ny=1$ diophantoszi egyenlet megoldásával, a fenti eljárással az $a$ modális inverzét is meg tudjuk határozni.

 

A cikk folytatása a szeptemberi számban lesz olvasható.