Az első, testek statikai egyensúlyával kapcsolatos eredmények Arkhimédész nevéhez fűződnek, mely eredményeket még a 17. századi hajóépítők is használták. A statikai egyensúlyi pontok vizsgálata végigvonul a fizika és a mérnöki tudományok történetén.
Mi is egy test egyensúlyi pontja? Mi az alábbi módon fogalmazzuk meg.

 

1. ábra. Egy gömb minden pontja egyensúlyi pont a tömegközéppontra nézve,
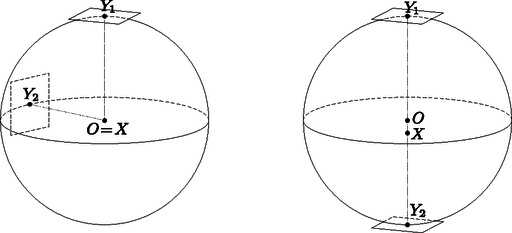de más pontra nézve csak a hozzá legközelebbi, illetve a tőle legtávolabbi
pontok egyensúlyi pontok

 

Bizonyítás. Legyen $T$ egy tetszőleges tetraéder, melynek csúcsai $A$, $B$, $C$ és $D$. A tetraéder súlypontját jelölje $S$, és az $A$-val szemközti háromszöglap súlypontját $S_A$. Legyen a tetraéder $A$-ból induló magasságának talppontja $M_A$, és $S$-nek a $BCD$ háromszög síkjára vett merőleges vetülete $X_A$. Legyen $m_A=\overline{A{M}_A}$ és $x_A=\overline{S{X}_A}$ (lásd 2. ábra). Hasonlóan definiáljuk az $S_B$, $S_C$ és $S_D$ pontokat, valamint az $m_B$, $x_B$, $m_C$, $x_C$, $m_D$, $x_D$ mennyiségeket.

 

 

2. ábra. Az $ABCD$ tetraéderre vonatkozó jelölések

 

Ismert, hogy a tetraéder súlypontja a tetraéder minden súlyvonalát $1:3$ arányban osztja, azaz

$\begin{array}{c}{\displaystyle \frac{\overline{A{S}_A}}{\overline{S{S}_A}}=\frac{\overline{B{S}_B}}{\overline{S{S}_B}}=\frac{\overline{C{S}_C}}{\overline{S{S}_C}}=\frac{\overline{D{S}_D}}{\overline{S{S}_D}}=4.}\end{array}$

Vegyük észre, hogy az $S{S}_A{X}_A$ és az $A{S}_A{M}_A$ háromszögek hasonlóak. A megfelelő oldalaik arányára így

$\begin{array}{c}{\displaystyle \frac{m_A}{x_A}=\frac{\overline{A{S}_A}}{\overline{S{S}_A}}=4}\end{array}$

adódik. Hasonlóan kapjuk az

$\begin{array}{c}{\displaystyle \frac{m_B}{x_B}=\frac{m_C}{x_C}=\frac{m_D}{x_D}=4}\end{array}$

egyenlőségeket. Mivel a tetraéder térfogatát úgy számolhatjuk ki, hogy tetszőleges lap területét megszorozzuk a hozzátartozó magasság harmadával, azt kapjuk, hogy a súlypont tetszőleges két lap közül pontosan ahhoz van közelebb, melynek a területe nagyobb.
Egy lapon pontosan akkor van stabil egyensúlyi pont, ha $S$ merőleges vetülete a lap síkjára a lap belsejébe esik. Másrészt, mivel a súlypont a tetraéder egy belső pontja, a tetraéder egyik lapjáról csak úgy billenhet át egy másik lapjára, ha a két lap közti lapszög tompaszög. A billenés után a súlypont lejjebb kerül, azaz a tetraéder csak olyan lapjára tud átbillenni, amelynek a síkjához a súlypont közelebb van. Az előző bekezdésben meggondoltak szerint így a tetraéder csak kisebb területű lapról egy nagyobb területű lapra tud átbillenni.
Tegyük most fel, hogy $T$-nek csak egy stabil lapja van. Vegyük észre, hogy a fentiek szerint a stabil lap így a legnagyobb területű lap. Legyen $T$ legnagyobb lapja $BCD$, és a második legnagyobb lapja $ACD$. A tetraéder egy harmadik lapja így vagy először az $ACD$ lapra, és arról a $BCD$ lapra gördül, vagy ez a lap és az $ACD$ lap is közvetlenül a $BCD$ lapra gördül. Mindkét esetben igaz az, hogy a két legnagyobb lap egyikéhez két derékszögnél nagyobb lapszög tartozik, és az egyik ilyen lapszög a két legnagyobb lap közti lapszög. Jelölje ezt a lapot $F$, és a tetraéder negyedik lapját $G$. Ekkor $F$ és $G$ szöge hegyesszög, és $G$ merőleges vetülete $F$ síkjára szigorúan tartalmazza $F$-et. De így $F$ területe határozottan kisebb, mint $G$ területe, ami ellentmond annak a feltevésnek, hogy $F$ a két legnagyobb, $G$ pedig a két legkisebb területű lap egyike.  $\square$

 

1967-ben Heppes Aladár [6] konstruált egy $T$ tetraédert egy érdekes, a fenti problémához kapcsolódó tulajdonsággal: a Heppes-féle `double-tipping' tetraédernek két lapján található stabil pont, és egy harmadik lapján megtámasztva a tetraéder először a negyedik lapra gördül, mielőtt találna egy egyensúlyi helyzetet valamelyik stabil lapon. Hogyan is néz ki ez a tetraéder? Ezt mutatjuk meg a továbbiakban.
Legyen $A=\left(-7;-7;0\right)$, $B=\left(-1;0;0\right)$, $C=\left(1;0;0\right)$ és $D=\left(7;8;8\right)$ egy $T$ tetraéder négy csúcsa. Ekkor a tetraéder alaplapja az $\left(x\mathrm{,}y\right)$-koordinátasíkban helyezkedik el, és súlypontja, melynek koordinátáit az egyes csúcsok megfelelő koordinátájaként számolhatjuk ki, az $S=\left(0;\mathrm{0,25};2\right)$ pont, melynek vetülete az alaplap síkjára $S\text{'}=\left(0;\mathrm{0,25};0\right)$. A tetraéder alaplapja az $ABC$ lap, amin az $S\text{'}$ pont kívül esik, tehát $T$ ebből a helyzetből átfordul egy másik lapra.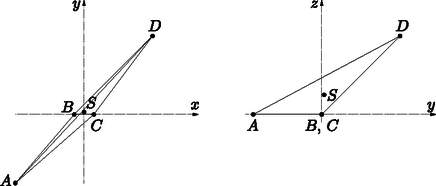

 

 

3. ábra. A $T$ tetraéder vetülete az $\left(x\mathrm{,}y\right)$ és az $\left(y\mathrm{,}z\right)$ síkokra

 

A $D$ csúcs vetülete az $ABC$ lap síkjára a $D\text{'}=\left(7;8;0\right)$ pont, ami az $A$, $B$ és $C$ pontokkal együtt egy konvex négyszöget alkot. Ebből látható, hogy az $ABCD$ tetraéder $AB$ és $AC$ élénél levő lapszöge hegyesszög, tehát az $ABC$ lapról $T$ a $BC$ él mentén, vagyis az $x$-tengely körül fordul át a $BCD$ lapra.
Vegyük észre, hogy mind az $ABC$, mind a $BCD$ lap merőleges az $\left(y\mathrm{,}z\right)$-koordinátasíkra. A tetraéder csúcsainak merőleges vetületei erre a síkra rendre $\overline{A}=\left(0;-7;0\right)$, $\overline{B}=\overline{C}=\left(0;0;0\right)$ és $\overline{D}=\left(0;8;8\right)$. Ebből látható, hogy a $T$ tetraéder $BC$ élénél levő lapszöge ${135}^{\circ }$, azaz az átfordulás szöge az $x$-tengely körül ${45}^{\circ }$. Minthogy a forgás során a pontok $x$-koordinátái nem változnak, kiszámolhatóak az elfordult $T_f$ tetraéder csúcsainak koordinátái, melyek rendre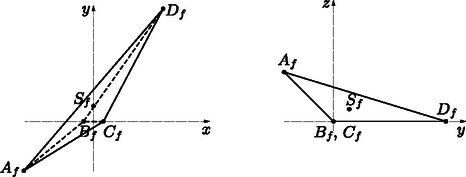

${\displaystyle \begin{array}{cc}\hfill {\displaystyle A_f}& {\displaystyle =\left(-7;-\mathrm{3,5}\sqrt[]{2};\mathrm{3,5}\sqrt[]{2}\right);B_f=B=\left(-1;0;0\right);}\hfill \\ \hfill {\displaystyle C_f}& {\displaystyle =C=\left(1;0;0\right);D_f=\left(7;8\sqrt[]{2};0\right)\mathrm{.}}\hfill \end{array}}$

A $T_f$ tetraéder súlypontja, és ennek vetülete az $\left(x\mathrm{,}y\right)$-koordinátasíkra rendre

$\begin{array}{c}{\displaystyle S_f=\left(0;1\mathrm{,}125\sqrt[]{2};0\mathrm{,}875\sqrt[]{2}\right);S{\text{'}}_f=\left(0;1\mathrm{,}125\sqrt[]{2};0\right)\mathrm{.}}\end{array}$

 

 

4. ábra. Az elfordult $T_f$ tetraéder vetülete az $\left(x\mathrm{,}y\right)$ és az $\left(y\mathrm{,}z\right)$ síkokra

 

Könnyen kiszámolható, hogy $S{\text{'}}_f$ kívül esik az átfordult tetraéder $B_f{C}_f{D}_f$ alaplapján. Így a tetraédernek ez a lapja sem stabil, azaz $T_f$ ebből a helyzetből is átfordul valamelyik éle mentén egy harmadik lapjára, mely az első tételünk szerint stabil.

 

Láttuk, hogy minden tetraédernek legalább két stabil lapja van. Esetleg igaz-e az is, hogy minden konvex poliédernek van legalább két stabil lapja? Conway és Guy [2] alábbi konstrukciója mutatja, hogy ez viszont nem igaz.

 

2. tétel. Van olyan $19$ lapú $K$ konvex poliéder, melynek pontosan egy stabil lapja van a tömegközéppontjára nézve.

 

A bizonyítás ötlete Először egy $A$ $\left(2n-1\right)$-szöget definiálunk az $\left(x\mathrm{,}y\right)$-síkon az alábbi módon, ahol $n\ge 2$.
Legyen $\beta =\frac{\pi }{n}$, és $P_1{P}_{2}O$ egy olyan derékszögű háromszög, melyben $\overline{O{P}_1}=1$, $P_{1}O{P}_2\sphericalangle =\beta$ és $P_1{P}_{2}O\sphericalangle =\frac{\pi }{2}$ (ld. 5. ábra). Írjunk a háromszög $O{P}_2$ befogójára egy $O{P}_2{P}_3$ háromszöget, mely hasonló az $O{P}_1{P}_2$ háromszöghöz, átfogója $O{P}_2$, és $O$-nál levő szöge $\beta$. Ezen háromszög $O{P}_3$ befogójára ugyancsak írjunk egy hasonló háromszöget, melynek átfogója $O{P}_3$, és $O$-nál levő szöge $\beta$. Az eljárást folytatjuk, amíg eljutunk az $O{P}_n{P}_{n+1}$ háromszöghöz, amely ugyancsak hasonló az $O{P}_1{P}_2$ háromszöghöz, átfogója $O{P}_n$, és $O$-nál levő szöge $\beta$. Ekkor $\beta$ definíciója miatt a $P_1$, $O$, $P_{n+1}$ pontok egy egyenesen vannak, és a $P_n{P}_{n+1}O$ szög derékszög.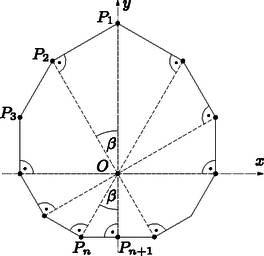

 

5. ábra. Az $A$ $\left(2n-1\right)$-szög konstrukciója

 

Trigonometrikus függvények használatával könnyen látható, hogy $\overline{O{P}_2}=\text{cos}\beta$, $\overline{O{P}_3}=\text{cos}{}^2\beta$, illetve általában $\overline{O{P}_i}=\text{cos}{}^{i-1}\beta$ minden $i=\mathrm{1,2,}\text{...}\mathrm{,}n+1$ esetén, azaz speciálisan $P_n$ és $P_{n+1}$ rajta vannak az $\left(x\mathrm{,}y\right)$-sík $y=-\text{cos}{}^n\beta$ egyenletű egyenesén.
A $P_2\mathrm{,}{P}_3\mathrm{,}\text{...}\mathrm{,}{P}_n$ pontokat tükrözzük az $y$-tengelyre, és jelölje a tükörképeket rendre $P_2\text{'}\mathrm{,}{P}_3\text{'}\mathrm{,}\text{...}\mathrm{,}{P}_n\text{'}$. A konstruálni kívánt $A$ sokszöget a $P_1{P}_2\text{...}{P}_n{P}_n\text{'}\text{...}{P}_2\text{'}$ töröttvonal határolta konvex sokszögként definiáljuk. Vegyük észre, hogy az $O{P}_{n+1}$ szakasz tetszőleges belső pontjára igaz, hogy $A$ oldalegyeneseire vett merőleges vetületei közt egyetlenegy van, amelyik $A$-nak is pontja; ez a pont a $P_{n+1}$ pont a $P_n{P}_n\text{'}$ oldal egyenesén. Ez az észrevétel lesz az alapja a konstrukciónknak.
Legyen $G$ az a végtelen gúla, melyet úgy kapunk, hogy $A$ minden pontjában merőlegest bocsátunk az $\left(x\mathrm{,}y\right)$-síkra, és vesszük az összes így keletkezett egyenes unióját. Ebből a végtelen gúlából egy korlátos $K$ gúlát fogunk konstruálni úgy, hogy elmetsszük két $S_1$, $S_2$ síkkal, melyek szimmetrikusak az $\left(x\mathrm{,}y\right)$-síkra, és merőlegesek az $\left(x\mathrm{,}z\right)$-síkra (ld. 6. ábra). Ezen síkok metszete az $\left(y\mathrm{,}z\right)$-síkkal egy-egy egyenes. Az $S_1$, $S_2$ síkokat úgy választjuk, hogy $S_1$ tartalmazza a $Q\left(0;1;a\right)$ és az $R\left(0;-\text{cos}{}^n\beta \mathrm{,}a+b\right)$ pontot, ahol $a\mathrm{,}b>0$, és az $S_2$ sík $S_1$ tükörképe az $\left(x\mathrm{,}y\right)$-síkra. $\left(2n-1\right)$-szög. A poliéder szimmetriái miatt látható, hogy a poliéder súlypontja a $P_1{P}_{n+1}$ szakasz egy pontja.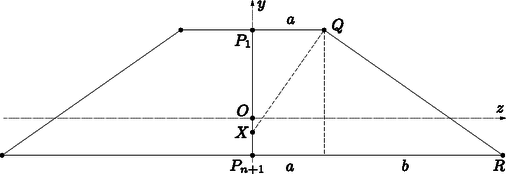

 

 

6. ábra. A $K$ csonkolt gúla $\left(y\mathrm{,}z\right)$-síkra vett merőleges vetületének képe

 

Állítsunk merőlegest az $S_1$ síkra a $Q$ pontban, és a merőleges egyenes $y$-tengellyel vett metszéspontját jelölje $X$. Ha a poliéder súlypontja az $OX$ szakasz egy belső pontja, akkor $K$-nak csak egy stabil lapja van; ez a lap a $P_{n}P{\text{'}}_n$ szakaszt tartalmazó lap. Megmutatjuk, hogy ha $a$ értéke rögzített és $b$ értéke nagyon nagy $a$-hoz képest, akkor $n=9$ esetén ez teljesül.
Ha $b\gg a$, akkor $P_{n+1}\in OX$, tehát csak azt kell megvizsgálnunk, hogy a súlypont $y$-koordinátája negatív-e. Kiszámolható, hogy a $t=\text{cos}\beta$ jelöléssel a súlypont $y$-koordinátája

$\begin{array}{c}{\displaystyle y_s=-\frac{t}{12\text{sin}\beta }[-2a\left(1+t^{3n}\right)\frac{\left(1-t^2\right)\left(1+2t^2\right)}{1+t^2-t^4}+\frac{b}{1+t^n}\cdot }\end{array}$

$\begin{array}{c}{\displaystyle \cdot \left(\left(1-t^{4n}\right)\frac{1+2t^2+4t^4+2t^6-3t^8}{\left(1+t^2\right)\left(1+t^2+3t^4-t^6\right)}-2\left(1+t^{3n}\right)\frac{\left(1-t^2\right)\left(1+2t^2\right)}{1+t^2-t^4}\right)]\mathrm{,}}\end{array}$

amiből látható, hogy $b\gg a$ esetén, ha a második sorban levő kifejezés pozitív, akkor $y_s$ negatív. Számolással adódik, hogy a legkisebb $n$ érték, melyre ez teljesül, $n=9$. Ebben az esetben $K$ egy $19$ lapú, pontosan egy stabil lappal rendelkező poliéder.
  $\square$

 

A fenti eredmények több további kérdést is felvetnek.
(1) Van-e inhomogén sűrűségű tetraéder, melynek pontosan egy stabil lapja van?
(2) Mennyi a monostabil, azaz (a súlypontjukra) pontosan egy stabil lappal rendelkező konvex poliéderek lapszámának minimuma?
(3) Speciálisan, igaz-e, hogy a négyszög alaplapú gúlák közt nincs monostabil?
(4) Egyensúlyi ponttal rendelkező lapok helyett egyensúlyi ponttal rendelkező csúcsokat is vizsgálhatunk. Ezekre igaz-e az első tételünk ,,duális'' változata, azaz igaz, hogy minden tetraédernek van legalább kettő egyensúlyi ponttal rendelkező csúcsa?
Az első kérdésre Conway adta meg az igenlő választ, melyről bővebb információ található a [4] cikkben.
Jelölje a monostabil poliéderek minimális lapszámát $l_m$. Ekkor az eddig ismertetett eredményeket az $5\le l_m\le 19$ egyenlőtlenségekben foglalhatjuk össze. A második kérdést illetően Conway eredménye, mely szerint $l_m\le 19$, meglepően sokáig a legjobb felső becslés maradt $l_m$ értékére. Az első javítás Bezdek Andrásnak [1] köszönhető, aki, ugyancsak elemi geometriai módszerekkel, 2011-ben konstruált egy $18$ lapú monostabil poliédert. Ezt 2014-ben Reshetov [7] javította $14$-re számítógépes módszerek alkalmazásával. A harmadik, Conway és Guy által 1969-ben feltett kérdés, hogy a négyszöglapú gúlák közt van-e monostabil, még ma is nyitott.
Az utolsó kérdésre igenlő a válasz (ld. [5]), de ennek tárgyalása meghaladja ezen cikk kereteit.

 

Hivatkozások

[1]	A. Bezdek, On stability of polyhedra, in: Workshop on Discrete Geometry, Sept. 13‐16, 2011, Fields Institute, Canada, 2490‐2491.

[2]	J. H. Conway, M. Goldberg and R. K. Guy, Problem 66-12, SIAM Rev. 11 (1969), 78‐82.

[3]	R. Dawson, Monostatic simplexes, Amer. Math. Monthly, 92 (1985), 541‐546.

[4]	R. Dawson and W. Finbow, What shape is a loaded die?, Math. Intelligencer, 22 (1999), 32‐37.

[5]	G. Domokos, F. Kovács, Z. Lángi, K. Regős and P.T. Varga, Balancing polyhedra, arXiv:1810.05382 [math.MG], October 12, 2018.

[6]	A. Heppes A double-tipping tetrahedron, SIAM Rev., 9 (1967), 599‐600.

[7]	A. Reshetov, A unistable polyhedron with $14$ faces (English summary), Internat. J. Comput. Geom. Appl., 24 (2014), 39‐59.