Cím:	Megoldásvázlatok a 2019/3. szám emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Németh László (Fonyód)
Füzet:	2019/április, 205 - 217. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Oldjuk meg a valós számok halmazán az alábbi egyenleteket: $a)$ ${\displaystyle \frac{2x}{x-1}}+{\displaystyle \frac{3}{x+1}}={\displaystyle \frac{6}{1-x^2}}$,  (4 pont)   $b)$ $\text{cos}\left(2x\right)+5\text{sin}x=3$,  (5 pont)   $c)$ $|x-2|+x=4\sqrt[]{x}-2$.  (5 pont)   Megoldás. $a)$ ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{2x}{x-1}+\frac{3}{x+1}=-\frac{6}{\left(x-1\right)\left(x+1\right)}/\cdot \left(x-1\right)\left(x+1\right)\mathrm{,}x\ne \pm 1}\hfill \\ \hfill {\displaystyle 2x\left(x+1\right)+3\left(x-1\right)=-6;2x^2+5x+3=0;x_{\mathrm{1,2}}=\frac{-5\pm \sqrt[]{25-24}}{4}\mathrm{.}}\hfill \end{array}}$ $x_1=-1$, ez a kikötés miatt nem gyöke az egyenletnek; $x_2=-\frac{3}{2}$. Az egyenlet megoldása: $x=-1\mathrm{,}5$. (Ellenőrzés: $-4\mathrm{,}8=-4\mathrm{,}8$.) ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 1-2\text{sin}{}^{2}x+5\text{sin}x=3;0=2\text{sin}{}^{2}x-5\text{sin}x+2;}\hfill & \text{(<mi>*</mi>)}\\ \hfill {\displaystyle {\left(\text{sin}x\right)}_{\mathrm{1,2}}=\frac{5\pm \sqrt[]{25-16}}{4}=\frac{5\pm 3}{4}\mathrm{.}}\hfill \end{array}}$ ${\left(\text{sin}x\right)}_1=2$ nem lehetséges; ${\left(\text{sin}x\right)}_2=\frac{1}{2}\Rightarrow x_1=\frac{\pi }{6}+2k\pi$, $\left(k\in \text{Z}\right)$; $x_2=\frac{5\pi }{6}+2l\pi$, $\left(l\in \text{Z}\right)$. (Ellenőrzés: $\frac{1}{2}+\frac{5}{2}=3$.)   $c)$ Kikötés: $0\le x$. Ha $2\le x$, akkor $x-2+x=4\sqrt[]{x}-2$; $2x=4\sqrt[]{x}$, innen $\sqrt[]{x}\left(\sqrt[]{x}-2\right)=0\Rightarrow x_1=0$; $x_2=4$; az $x_1$ kisebb 2-nél, tehát nem megoldás, a 4 azonban igen. Ha $x<2$, akkor $-\left(x-2\right)+x=4\sqrt[]{x}-2$; ebből a $4=4\sqrt[]{x}$ egyenletet kapjuk, aminek a megoldása $x_3=1$. Az egyenlet gyökei tehát $x_2=4$; $x_3=1$. (Ellenőrzés: $2=2$, illetve $6=6$.)     2. Egy háromszögben az egyik oldal kétszer akkora, mint egy másik oldal; az előbbivel szemközti szög ${60}^{\circ }$-kal nagyobb az utóbbival szemközti szögnél. A háromszög területe $2\sqrt[]{3}$ területegység. Mekkorák a háromszög oldalai és szögei?   (12 pont)   Megoldás. Legyen a $c$ oldal kétszerese $a$-nak, így $\gamma =\alpha +{60}^{\circ }$, írjuk fel a szinusz-tételt: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{\text{sin}\left(\alpha +{60}^{\circ }\right)}{\text{sin}\alpha }=\frac{2a}{a}\mathrm{,}\text{sin}\left(\alpha +{60}^{\circ }\right)=2\text{sin}\alpha ;}\hfill \\ \hfill {\displaystyle \text{sin}\alpha \cdot \text{cos}{60}^{\circ }+\text{cos}\alpha \cdot \text{sin}{60}^{\circ }=2\text{sin}\alpha ;\text{sin}\alpha \cdot \frac{1}{2}+\text{cos}\alpha \cdot \frac{\sqrt[]{3}}{2}=2\text{sin}\alpha ;}\hfill \\ \hfill {\displaystyle \frac{\sqrt[]{3}}{2}\cdot \text{cos}\alpha =\frac{3}{2}\text{sin}\alpha /\cdot \frac{2}{3}\mathrm{,}:\text{cos}\alpha \ne 0;}\hfill \\ \hfill {\displaystyle \text{tg}\alpha =\frac{\sqrt[]{3}}{3}\Rightarrow \alpha ={30}^{\circ };\gamma ={90}^{\circ };\beta ={60}^{\circ }\mathrm{.}}\hfill \end{array}}$ Alkalmazzuk a trigonometrikus területképletet:   $\frac{a\cdot \left(2a\right)\text{sin}{60}^{\circ }}{2}=2\sqrt[]{3}$; $a^2\frac{\sqrt[]{3}}{2}=2\sqrt[]{3}$; innen $a^2=4\Rightarrow a=2$, $c=4$, $b=\frac{\sqrt[]{3}}{2}\cdot 4=2\sqrt[]{3}$. Megkaptuk a keresett adatokat.     3. $a)$ Igaz-e az $A$, $B$ kijelentések tetszőleges logikai értékénél, hogy $\begin{array}{c}{\displaystyle \left(\left(\neg A\to \neg B\right)^A\right)\to B=\text{i}?}\end{array}$ $\left(\neg A=\text{nem }A\mathrm{.}\right)$  (5 pont) $b)$ Igaz-e, ha $\underset{n\to \infty }{\overset{}{\underset{}{\overset{}{\text{lim}}}}}\left(a_n+b_n\right)=0$, akkor $\underset{n\to \infty }{\overset{}{\underset{}{\overset{}{\text{lim}}}}}\left(a_n\right)+\underset{n\to \infty }{\overset{}{\underset{}{\overset{}{\text{lim}}}}}\left(b_n\right)=0$? Válaszunkat indokoljuk.  (3 pont) $c)$ Hány pontja lehet annak az egyszerű, összefüggő gráfnak, amelynek $8$ éle van?  (4 pont)   Megoldás. $a)$ A válasz: NEM, az indoklás:   ${\displaystyle \begin{array}{|ccccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>¬</mo><mi>A</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>¬</mo><mi>B</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>¬</mo><mi>A</mi><mo stretchy="true">→</mo><mo>¬</mo><mi>B</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">(</mo><mrow><mo>¬</mo><mi>A</mi><mo stretchy="true">→</mo><mo>¬</mo><mi>B</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo>∧</mo><mi>A</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">(</mo><mrow><mrow><mo fence="true" stretchy="true">(</mo><mrow><mo>¬</mo><mi>A</mi><mo stretchy="true">→</mo><mo>¬</mo><mi>B</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo>∧</mo><mi>A</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="true">→</mo><mi>B</mi></math> }}\hfill \\ \hfill {\displaystyle \text{i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i }}\hfill \\ \hfill {\displaystyle \text{i}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ h }}\hfill \\ \hfill {\displaystyle \text{h}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ i }}\hfill \\ \hfill {\displaystyle \text{h}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ i }}\hfill \\ \hline\end{array}}$   Azaz, ha $A=\text{i}$, $B=\text{h}$, akkor a művelet eredménye hamis.   Megjegyzés. Itt az a tipikusan hibás következtetés van kicsit átfogalmazva, amit gyakran tapasztalhatunk: ,,Ha $A$, akkor $B$, mivel nem $A$, tehát nem $B$''.   $b)$ A válasz: NEM. Elég egy megfelelő ellenpéldát mutatni.     $c)$ A pontok száma nem lehet 4, vagy annál kevesebb, mert az ilyen gráfok éleinek száma legfeljebb 6 lehet (ha a 4 pontú gráf teljes gráf). Az $n$ pontú legkevesebb élt tartalmazó összefüggő gráf (fa gráf) éleinek száma $n-1$. Ha $n-1=8$, akkor $n=9$. A gráf pontjainak száma nem lehet 9-nél nagyobb, mert akkor nem lenne összefüggő. A megoldás tehát: $5\le n\le 9$, azaz legalább 5 és legfeljebb 9. Ezek mindegyike előállítható.     4. $a)$ Hány olyan kétjegyű szám van, amelyben a számjegyek különbségének abszolút értéke legfeljebb $3?$  (8 pont) $b)$ Ha ezek közül véletlenszerűen kiválasztunk kettő különböző számot, mennyi a valószínűsége annak, hogy az egyik páros, a másik páratlan lesz?  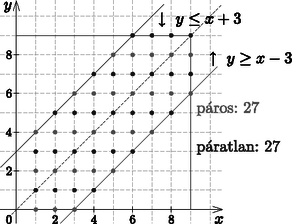(5 pont)   Megoldás. $a)$ Legyen a kétjegyű szám első jegye $x$, a második $y$, ahol $1\le x\le 9$, $0\le y\le 9$ és $x\mathrm{,}y\in N$. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle |x-y|\le \mathrm{3,}}& {\displaystyle \text{ha <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>≤</mo><mi>x</mi></math>, akkor }x-y\le 3\Rightarrow y\ge x-3;}\hfill \\ \hfill {\displaystyle }& {\displaystyle \text{ha <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo>≤</mo><mi>y</mi></math>, akkor }y-x\le 3\Rightarrow y\le x+3.}\hfill \end{array}}$ Ábrázolva az egyeneseket, a megadott tartományban 54 rácspont van, azaz 54 ilyen szám van.   $b)$ Az ábráról az is könnyen leolvasható, hogy 27 páros, 27 páratlan szám van közöttük, így $\begin{array}{c}{\displaystyle P\left(A\right)=\frac{\left(\genfrac{}{}{0ex}{}{27}{1}\right)\cdot \left(\genfrac{}{}{0ex}{}{27}{1}\right)}{\left(\genfrac{}{}{0ex}{}{54}{2}\right)}=\frac{27\cdot 27}{\frac{54\cdot 53}{2\cdot 1}}=\frac{27}{53}\mathrm{.}}\end{array}$   II. rész     5. Egy téglalap oldalainak mérőszáma egész szám. Ezt a téglalapot oldalaival párhuzamos egyenesekkel egységnégyzetekre daraboltuk, majd a széleken levőket fehérre, a többit feketére festettük. $a)$ Mekkorák a téglalap oldalai, ha kétszer annyi fekete négyzet lett, mint amennyi fehér?  (9 pont) $b)$ Az $a)$ részben kapott téglalapokból kiválasztottuk azt, amelynek oldalméretei között legkisebb a különbség, majd egy $8$ egység sugarú piros körlap közepére erősítettük. Az így kapott eszközt céltáblának használjuk, ahol a telitalálatot az jelenti, ha fehér mezőbe csapódik a lövedék. Feltesszük, hogy minden lövés eltalálja a céltáblát, és annak minden pontját egyenlő valószínűséggel. Mekkora a valószínűsége, hogy Vilmos négy lövésből legalább kétszer telitalálatot ér el? Az eredményt százalékban egészre kerekítve fejezzük ki.  (7 pont)   Megoldás. $a)$ A téglalap oldalainak hosszát jelölje $n$, $k$ ($n\mathrm{,}k\in {\text{Z}}^{+})$, a fekete négyzetek száma $\left(n-2\right)\left(k-2\right)$, ez kétharmada az összes négyzet számának, vagyis ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{2}{3}n\cdot k=\left(n-2\right)\left(k-2\right);2nk=3\left(nk-2n-2k+4\right);}\hfill \\ \hfill {\displaystyle 0=nk-6n-6k+12/+24;}\hfill \\ \hfill {\displaystyle 24=nk-6n-6k+36;24=\left(n-6\right)\left(k-6\right);24=2^3\cdot \mathrm{3,}}\hfill \end{array}}$ ezért a 24-nek 8 pozitív osztója van. A lehetséges párosítások: ${\displaystyle \begin{array}{cccc}\hfill {\displaystyle n-6=\mathrm{1,}}& {\displaystyle k-6=24;}\hfill & {\displaystyle n-6=\mathrm{2,}}\hfill & \hfill {\displaystyle k-6=12;}\\ \hfill {\displaystyle n-6=\mathrm{3,}}& {\displaystyle k-6=8;}\hfill & {\displaystyle n-6=\mathrm{4,}}\hfill & \hfill {\displaystyle k-6=6.}\end{array}}$ (A többi ugyanezeket a számpárokat adja felcserélve.) A téglalap két oldalának hosszára tehát a következő lehetőségek adódnak:   ${\displaystyle \begin{array}{ccc}{\displaystyle \text{ 7, 30, }}\hfill & {\displaystyle \text{ ekkor }}\hfill & {\displaystyle \text{ 70 fehér, 140 fekete }}\hfill \\ {\displaystyle \text{ 8, 18, }}\hfill & {\displaystyle }\hfill & {\displaystyle \text{ 48 fehér, 96 fekete}}\hfill \\ {\displaystyle \text{ 9, 14, }}\hfill & {\displaystyle }\hfill & {\displaystyle \text{ 42 fehér, 84 fekete}}\hfill \\ \multicolumn{2}{c}{{\displaystyle \text{10, 12 (egység),}}}& {\displaystyle \text{ 40 fehér, 80 fekete négyzet keletkezett. }}\hfill \end{array}}$   $b)$ A céllaphoz választott téglalap a $10\times 12$-es lesz, itt a legkevesebb a különbség az oldalak hossza között. A középpontokat egymáshoz illesztve látható, hogy a téglalap a körlap belsejében van, a félátló kisebb a sugárnál ($5^2+6^2<8^2)$. Annak a valószínűsége, hogy egy lövés telitalálatot ér: $p=\frac{40}{8^2\pi }=0\mathrm{,}1989$, nem ér telitalálatot: $q=0\mathrm{,}8011$. Jelölje $\xi$ azt, hogy a négy lövésből hány telitalálat lett. $\xi$ lehetséges értékei: $\mathrm{0,1,2,3,4}$. $\begin{array}{c}{\displaystyle P\left(\xi =0\right)=\left(\genfrac{}{}{0ex}{}{4}{0}\right)p^0{q}^4=0\mathrm{,}4119;P\left(\xi =1\right)=\left(\genfrac{}{}{0ex}{}{4}{1}\right)p^1{q}^3=0\mathrm{,}4090.}\end{array}$ A komplementer esemény valószínűsége: $P\left(\xi =0\right)+P\left(\xi =1\right)=0\mathrm{,}4119+0\mathrm{,}4090=0\mathrm{,}8209$, ezért az esemény valószínűsége: $1-0\mathrm{,}8209=0\mathrm{,}1791$. Annak a valószínűsége, hogy Vilmos négy lövésből legalább kétszer telitalálatot ér el,$18\%$.     6. 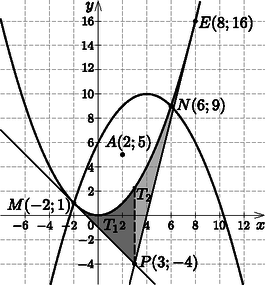$a)$ Az $f\left(x\right)=\frac{x^2}{4}$ függvény grafikonját tükrözzük az $A\left(2;5\right)$ pontra. Hol metszi az így kapott görbe az $f\left(x\right)$ grafikonját?  (5 pont) $b)$ Húzzunk érintőt a $P\left(3;-4\right)$ pontból $f\left(x\right)$ grafikonjához. Írjuk fel az érintők egyenletét.  (6 pont) $c)$ Mekkora a területe annak a síkidomnak, melyet az $f\left(x\right)$ függvény grafikonja és a $P\left(3;-4\right)$ ponton átmenő érintők zárnak közre?  (5 pont)   Megoldás. $a)$ Az $f\left(x\right)$ függvény grafikonja egy parabola, amelynek tengelypontja az origó, tengelye az $y$ tengely, paramétere 2. Az $A\left(2;5\right)$ pontra tükrözve a tengelypontja $T\text{'}\left(4;10\right)$ lesz, tengelye párhuzamos marad az $y$ tengellyel, lefelé nyílik, így egyenlete: $y-10=-\frac{1}{4}{\left(x-4\right)}^2$, $y$-ra rendezve: $y=-\frac{1}{4}{x}^2+2x+6$. (Ezt megkaphatjuk másképpen is. Legyen a $P\left(x;y\right)$ pont tükörképe az $A\left(2;5\right)$ pontra nézve $P\text{'}\left(x\text{'};y\text{'}\right)$, ekkor a felezőpont koordinátáira vonatkozó tétel szerint $\frac{x+x\text{'}}{2}=2$, $\frac{y+y\text{'}}{2}=5\Rightarrow x=4-x\text{'}$; $y=10-y\text{'}$. Ezeket beírva az $y=\frac{1}{4}{x}^2$-be kapjuk, hogy $4\left(10-y\text{'}\right)={\left(4-x\text{'}\right)}^2$, ami rendezve: $y\text{'}=-\frac{1}{4}x{\text{'}}^2+2x\text{'}+6$, tehát ugyanaz, mint a korábban kapott egyenlet.) A két görbe metszéspontjait az $\frac{1}{4}{x}^2=-\frac{1}{4}{x}^2+2x+6$ egyenletből kapjuk. Rendezve: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{1}{2}{x}^2-2x-6=\mathrm{0,}}\hfill \\ \hfill {\displaystyle x_{\mathrm{1,2}}=\frac{2\pm \sqrt[]{{\left(-2\right)}^2-4\cdot \frac{1}{2}\cdot \left(-6\right)}}{2\cdot \frac{1}{2}}=\frac{2\pm \sqrt[]{16}}{1}\mathrm{,}}\hfill \\ \hfill {\displaystyle x_1=6;y_1=\mathrm{9,}}\hfill \\ \hfill {\displaystyle x_2=-2;y_2=1.}\hfill \end{array}}$ A metszéspontok: $M\left(-2;1\right)$, $N\left(6;9\right)$.   $b)$ A $P\left(3;-4\right)$ ponton átmenő, $m$ meredekségű egyenes egyenlete: $y-\left(-4\right)=m\left(x-3\right)$; $y=mx-3m-4$. Ezt beírva $y$ helyére $mx-3m-4=\frac{1}{4}{x}^2$, majd rendezve az $x^2-4mx+12m+16=0$ paraméteres másodfokú egyenletet kaptuk, amelynek egy megoldása van a két görbe érintkezése miatt, vagyis $D=0$, azaz ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\left(-4m\right)}^2-4\cdot 1\cdot \left(12m+16\right)=0;16m^2-48m-64=0/:16;}\hfill \\ \hfill {\displaystyle m^2-3m-4=0;m_{\mathrm{1,2}}=\frac{3\pm \sqrt[]{9+16}}{2}\Rightarrow m_1=4;m_2=-1.}\hfill \end{array}}$ Az érintők egyenlete: $y=4x-16$, $y=-x-1$.   Eljuthatunk az érintők egyenletéhez más módon is. Az $f\left(x\right)$ függvény deriváltja $f\text{'}\left(x\right)=\frac{1}{4}\cdot 2x=\frac{1}{2}x$. A parabola $P_0(x_0;\frac{1}{4}{x}_0^2)$ pontjához húzott érintő meredeksége $m=f\text{'}\left(x_0\right)=\frac{1}{2}{x}_0$, az érintő egyenlete $\begin{array}{c}{\displaystyle y-\frac{1}{4}{x}_0^2=\frac{1}{2}{x}_0\left(x-x_0\right);y=\frac{1}{2}{x}_{0}x-\frac{1}{4}{x}_0^2\mathrm{.}}\end{array}$     Ennek az egyenesnek pontja a $P\left(3;-4\right)$ pont, tehát: $\begin{array}{c}{\displaystyle -4=\frac{1}{2}{x}_0\cdot 3-\frac{1}{4}{x}_0^2;}\end{array}$ rendezve: ${\displaystyle \begin{array}{c}\hfill {\displaystyle x_0^2-6x_0-16=0;}\hfill \\ \hfill {\displaystyle {\left(x_0\right)}_{\mathrm{1,2}}=\frac{6\pm \sqrt[]{36+64}}{2}\Rightarrow }\hfill \\ \hfill {\displaystyle {\left(x_0\right)}_1=8;{\left(x_0\right)}_2=-2.}\hfill \end{array}}$ Megkaptuk az érintési pontok első koordinátáit. (Ezek egyébként kellenek majd a $c)$ részhez.) Az érintők egyenlete: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle y}& {\displaystyle =\frac{1}{2}\cdot 8x-\frac{1}{4}\cdot 8^2=4x-16;}\hfill \\ \hfill {\displaystyle y}& {\displaystyle =\frac{1}{2}\cdot \left(-2\right)\cdot x-\frac{1}{4}\cdot {\left(-2\right)}^2=-x-1.}\hfill \end{array}}$ $c)$ Az érintési pontok abszcisszái az $x_{\mathrm{1,2}}=\frac{4m}{2}$ egyenletből adódnak (illetve a $b)$ rész második megoldásából már ismerjük őket), $m=4$ esetén 8; $m=-1$ esetén $-2$ lesz értékük. A területszámítást két részre bontjuk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_1}& {\displaystyle =\underset{-2}{\overset{3}{\int }}\left(\frac{1}{4}{x}^2-\left(-x-1\right)\right)\text{d}x={\left[\frac{1}{4}\frac{x^3}{3}+\frac{1}{2}{x}^2+x\right]}_{-2}^3=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{1}{4}\cdot \frac{27}{3}+\frac{1}{2}\cdot 9+3-\left(\frac{1}{4}\cdot \frac{-8}{3}+\frac{1}{2}\cdot 4-2\right)=\frac{125}{12}\mathrm{,}}\hfill \\ \hfill {\displaystyle T_2}& {\displaystyle =\underset{3}{\overset{8}{\int }}\left(\frac{1}{4}{x}^2-\left(4x-16\right)\right)\text{d}x={\left[\frac{1}{4}\cdot \frac{x^3}{3}-4\frac{x^2}{2}+16x\right]}_3^8=\frac{128}{3}-\frac{129}{4}=\frac{125}{12}\mathrm{.}}\hfill \end{array}}$ A síkidom területe $T=T_1+T_2=\frac{125}{6}$ területegység lett.   7. $a)$ Mutassuk meg, hogy minden $n$ természetes számra igaz, hogy $3\mid n^3+8n$.  (6 pont) $b)$ Oldjuk meg a $p+q^n=2019$ egyenletet, ahol $p$, $q$ pozitív prím, $n$ pozitív egész szám. Használjuk a függvénytáblázatot.  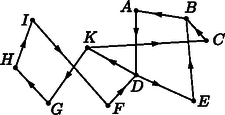(6 pont) $c)$ Nagy úr éppen most kísérte végig vendégeit a birtokán, amelynek során minden ajtón pontosan egyszer mentek át. A bemutató végén a nappaliban pezsgővel koccintottak a találkozásra. Melyik helyiség a nappali? A helyiségek betűjelének felsorolásával adjunk meg egy lehetséges bejárási sorrendet.  (4 pont) 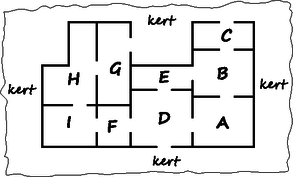    Nagy úr házának alaprajza     Megoldás. $a)$ I. megoldás. $n^3+8n=n\left(n^2+8\right)$, az $n$ 3-mal osztva 0-t, vagy $\pm 1$-et ad maradékul. Ha $n=3k$, akkor a szorzat első tényezője osztható 3-mal, így a szorzat is. Ha $n=3k\pm 1$, akkor ${\displaystyle \begin{array}{cc}\hfill {\displaystyle n^2}& {\displaystyle ={\left(3k\pm 1\right)}^2=9k^2\pm 6k+1;}\hfill \\ \hfill {\displaystyle n^2+8}& {\displaystyle =9k^2\pm 6k+9=3\left(3k^2\pm 2k+3\right)\mathrm{,}}\hfill \end{array}}$ ebben az esetben a második tényező osztható 3-mal. Ezzel bizonyítottuk az állítást.   II. megoldás. $\begin{array}{c}{\displaystyle n^3+8n=\left(n^3-n\right)+9n=n\left(n^2-1\right)+9n=n\left(n-1\right)\left(n+1\right)+9n\mathrm{.}}\end{array}$ Az átalakítás után a kéttagú kifejezés második tagja nyilván osztható 3-mal, az első tagban pedig három szomszédos egész szám szerepel, ezek egyike biztosan osztható 3-mal, így a szorzat is. Mivel két 3-mal osztható szám összege is osztható 3-mal, az állítás igaz.   (Megjegyzés. Itt felismerhetjük a ,,kis Fermat-tétel'' $p=3$-ra vonatkozó esetét: $p\mid n^p-n$, ahol $p$ prímszám, $n$ egész szám.)   III. megoldás: teljes indukcióval. $n=0$-ra igaz, tegyük fel, hogy $n$-re igaz, bizonyítjuk, hogy $\left(n+1\right)$-re is igaz: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left(n+1\right)}^3+8\left(n+1\right)}& {\displaystyle =n^3+3n^2+3n+1+8n+8=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\left(n^3+8n\right)+3\left(n^2+n+3\right)\mathrm{.}}\hfill \end{array}}$ Az első tag az indukciós feltétel miatt osztható 3-mal, a második is osztható 3-mal, így az összeg is.   $b)$ Az egyik prímnek 2-nek kell lennie, különben a bal oldal páros volna, nem lehetne az összeg 2019. Legyen $p=2$, ekkor $q^n=2017$. Mivel 2017 prím, így a $q=2017$, $n=1$ megoldást kaptuk. Legyen most $q=2$, ekkor $p=2019-2^n$. Az $n$ értéke legfeljebb 10 lehet, nagyobb $n$-re $p$ negatív lenne. Az áttekinthetőség kedvéért készítsük el az alábbi táblázatot:   ${\displaystyle \begin{array}{|ccccccccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>n</mi></math>}}\hfill & \hfill {\displaystyle \text{ 1}}\hfill & \hfill {\displaystyle \text{ 2}}\hfill & \hfill {\displaystyle \text{ 3}}\hfill & \hfill {\displaystyle \text{ 4}}\hfill & \hfill {\displaystyle \text{ 5}}\hfill & \hfill {\displaystyle \text{ 6}}\hfill & \hfill {\displaystyle \text{ 7}}\hfill & \hfill {\displaystyle \text{ 8}}\hfill & \hfill {\displaystyle \text{ 9}}\hfill & \hfill {\displaystyle \text{ 10 }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mn>2</mn></mrow><mrow><mi>n</mi></mrow></msup></mrow></math> }}\hfill & \hfill {\displaystyle \text{ 2}}\hfill & \hfill {\displaystyle \text{ 4}}\hfill & \hfill {\displaystyle \text{ 8}}\hfill & \hfill {\displaystyle \text{ 16}}\hfill & \hfill {\displaystyle \text{ 32}}\hfill & \hfill {\displaystyle \text{ 64}}\hfill & \hfill {\displaystyle \text{ 128}}\hfill & \hfill {\displaystyle \text{ 256}}\hfill & \hfill {\displaystyle \text{ 512}}\hfill & \hfill {\displaystyle \text{ 1024 }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>p</mi></math> }}\hfill & \hfill {\displaystyle \text{ 2017}}\hfill & \hfill {\displaystyle \text{ 2015}}\hfill & \hfill {\displaystyle \text{ 2011}}\hfill & \hfill {\displaystyle \text{ 2003}}\hfill & \hfill {\displaystyle \text{ 1987}}\hfill & \hfill {\displaystyle \text{ 1955}}\hfill & \hfill {\displaystyle \text{ 1891}}\hfill & \hfill {\displaystyle \text{ 1763}}\hfill & \hfill {\displaystyle \text{ 1507}}\hfill & \hfill {\displaystyle \text{ 995 }}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{ prím}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>5</mn><mo>⋅</mo><mn>403</mn></math>}}\hfill & \hfill {\displaystyle \text{ prím}}\hfill & \hfill {\displaystyle \text{ prím}}\hfill & \hfill {\displaystyle \text{ prím}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>5</mn><mo>⋅</mo><mn>391</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>31</mn><mo>⋅</mo><mn>61</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>41</mn><mo>⋅</mo><mn>43</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>11</mn><mo>⋅</mo><mn>137</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>5</mn><mo>⋅</mo><mn>199</mn></math> }}\hfill \\ \hline\end{array}}$   Megjegyzés. A függvénytáblázat 4000-ig felsorolja a prímeket, célszerű használni, de ha nem, akkor a 2015, 1955, 995 nyilván nem prím, a többiek sem oszthatók 2, 3, 5-tel, elég az osztásokat 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43-mal elvégezni $\left(\sqrt[]{2019}\approx 44\mathrm{,}93\right)$, ami ,,rabszolgamunka'', de viszonylag gyorsan elvégezhető. A megoldások tehát:  ${\displaystyle \begin{array}{|ccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>p</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>q</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>n</mi></math> }}\hfill \\ \hfill {\displaystyle \text{2}}\hfill & \hfill {\displaystyle \text{ 2017}}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill \\ \hfill {\displaystyle \text{2017}}\hfill & \hfill {\displaystyle \text{ 2}}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill \\ \hfill {\displaystyle \text{2011}}\hfill & \hfill {\displaystyle \text{ 2}}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill \\ \hfill {\displaystyle \text{2003}}\hfill & \hfill {\displaystyle \text{ 2}}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill \\ \hfill {\displaystyle \text{1987}}\hfill & \hfill {\displaystyle \text{ 2}}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill \\ \hline\end{array}}$   $c)$ Ábrázoljuk egy 10 pontú gráffal az egyes helyiségek ajtóval való összeköttetéseit (a kert is helyiség) úgy, hogy a pontokat (helyiségek) ott köti össze él, ahol ajtó van közöttük. A gráfban $K$ és $B$ foka 3, $D$-é 4, a többié 2.     Olyan útvonalat keresünk, amely minden élet pontosan egyszer érint, ez csak olyan lehet, amelyik $K$-ból indul és $B$-ben végződik, vagy fordítva, mert a többi pont páros foka miatt a végén (vagy elején) nem tartózkodhatnánk ott, hiszen az egyik élen érkeztünk, a másikon távoztunk (a $D$-nél ezt kétszer). A nappali tehát a $B$ helyiség. Egy lehetséges útvonal: $KCBADKGHIFDEB$ (nyitott Euler-vonal).     8. Egy kozmetikai cég saját termékét három változatban forgalmazza a hatóanyag töménységétől, a kiszerelés mennyiségétől és a csomagolástól függően. Az $A$ jelű termék 150 g-os, $10\%$ töménységű; a $B$ jelű 100 g-os, $20\%$ töménységű; a $C$ jelű 50 g-os, $30\%$ töménységű. A hatóanyag és az oldószer a termék árában a mennyiségével egyenes arányban jelenik meg; az $A$ és $B$ jelű termék csomagolása kétszer annyiba kerül, mint a $C$ jelű terméké. Az üzletben az $A$ 2275 Ft-ba, a $B$ 2500 Ft-ba, a $C$ pedig 1725 Ft-ba kerül dobozonként. $a)$ Mennyi a hatóanyag és az oldószer grammonkénti ára?  (7 pont) Anna egyik nap észrevette, hogy az üzlet egyik polcán az $A$, $B$, $C$ jelű termékekből annyi van, hogy számuk egy növekvő mértani sorozat három szomszédos elemével egyenlő. A számok átlaga $14$, szórása $2\sqrt[]{14}$. $b)$ Hány termék volt a polcon az egyes fajtákból?  (9 pont)   Megoldás. $a)$ A hatóanyag ára: $x$ Ft/g; az oldószeré $y$ Ft/g; a $C$ jelű termék dobozának ára $z$. Az $A$ jelű termékben 15 g hatóanyag és 135 g oldószer van, így az ára: $15x+135y+2z=2275$ (Ft). A $B$ jelűben 20 g hatóanyag és 80 g oldószer van, ára: $20x+80y+2z=$ =2500 (Ft). A $C$ jelűben 15 g hatóanyag és 35 g oldószer van, ára: $15x+35y+z=$ =1725 (Ft). A harmadik egyenletet szorozzuk meg $\left(-2\right)$-vel, majd adjuk hozzá a másik kettőhöz. Az elsőből: $-15x+65y=-1175/\cdot 2$; $-30x+130y=-2350$. A másodikból: $-10x+10y=-950$ $/\cdot \left(-3\right)$; $30x-30y=2850$. Összeadva $100y=500$. Ebből $y=5$, ezt beírva $-10x+50=-950$-be, $x$-re 100 adódik. A hatóanyag ára 100 Ft, az oldószeré 5 Ft grammonként. (A $C$ termék csomagolása 50, az $A$ és $B$ terméké pedig 100-100 Ft-ba került.) Ellenőrzéssel győződhetünk meg az eredmények helyességéről.   $b)$ Jelölje a termékek számát $\frac{a}{q}$, $a$, $aq$, ahol $0<a$, $1<q$, $a\in \text{N}$, $q\in \text{Q}$. ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{\frac{a}{q}+a+aq}{3}=14;a\left(q+\frac{1}{q}\right)=42-a;q+\frac{1}{q}=\frac{42}{a}-1;}\hfill \\ \hfill {\displaystyle {\left(q+\frac{1}{q}\right)}^2=\frac{1764}{a^2}-\frac{84}{a}+1;q^2+2+\frac{1}{q^2}=\frac{1764}{a^2}-\frac{84}{a}+1;}\hfill \\ \hfill {\displaystyle \text{innen}{q}^2+\frac{1}{q^2}=\frac{1764}{a^2}-\frac{84}{a}-1.}\hfill \\ \hfill {\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle \sqrt[]{{\displaystyle \frac{(14-\frac{a}{q}{)}^2+{\left(14-a\right)}^2+{\left(14-aq\right)}^2}{3}}}}& {\displaystyle =2\sqrt[]{14};}\hfill \\ \hfill {\displaystyle {\left(14-{\displaystyle \frac{a}{q}}\right)}^2+{\left(14-a\right)}^2+{\left(14-aq\right)}^2}& {\displaystyle =168;}\hfill \\ \hfill {\displaystyle 196-{\displaystyle \frac{28a}{q}}+{\displaystyle \frac{a^2}{q^2}}+196-28a+a^2+196-28aq+a^2{q}^2}& {\displaystyle =168;}\hfill \\ \hfill {\displaystyle a^2\left(q^2+{\displaystyle \frac{1}{q^2}}\right)-28a\left(q+{\displaystyle \frac{1}{q}}\right)+a^2-28a+420}& {\displaystyle =0;}\hfill \\ \hfill {\displaystyle a^2\left({\displaystyle \frac{1764}{a^2}}-{\displaystyle \frac{84}{a}}-1\right)-28a\left({\displaystyle \frac{42}{a}}-1\right)+a^2-28a+420}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle 1764-84a-a^2-1176+28a+a^2-28a+420}& {\displaystyle =0;}\hfill \end{array}}}\hfill \end{array}}$ ebből $1008=84a$, vagyis $a=12$ adódik. ${\displaystyle \begin{array}{c}\hfill {\displaystyle q+\frac{1}{q}=\frac{42}{12}-1;q+\frac{1}{q}=\frac{5}{2};2q^2-5q+2=0;}\hfill \\ \hfill {\displaystyle q_{\mathrm{1,2}}=\frac{5\pm \sqrt[]{25-16}}{4}=\frac{5\pm 3}{4}\Rightarrow q_1=\mathrm{2,}{q}_2=\frac{1}{2};}\hfill \end{array}}$ mivel $1<q$, ezért $q=2$. A polcon az $A$ jelűből 6, a $B$ jelűből 12, a $C$ jelűből 24 doboz volt.     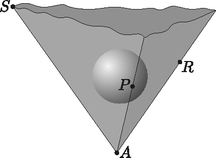9. A $2$ egység élű $ABCDEFGH$ csúcsú kocka $ABCD$ alaplapjának középpontja $P$; $DCGH$ oldallapjának középpontja $Q$; $AEHD$ előlapjának középpontja $R$; a $BF$ él felezőpontja $S$. $(A$-t $E$-vel, $B$-t $F$-fel, $C$-t $G$-vel, $D$-t $H$-val köti össze él.$)$ $a)$ Mekkora az $A$, $P$, $Q$, $R$, $S$ csúcsú poliéder térfogata?  (8 pont) $b)$ Mekkora a poliéderbe írt gömb sugara?  (8 pont)   Megoldás. $a)$ I. megoldás. A kocka $AHC$ csúcsai egy $2\sqrt[]{2}$ oldalú szabályos háromszöget alkotnak, amelynek oldalfelező pontjai a $P$, $Q$, $R$ pontok (1. ábra). Az $A$, $P$, $Q$, $R$ pontok tehát egy síkban vannak, a $PQR$ háromszög és az $APR$ háromszög egy-egy $\sqrt[]{2}$ oldalú szabályos háromszög, ezek együtt adják az $APQR$ rombuszt; így $APQRS$ egy rombusz alapú gúla (2. ábra). Az $SQ$, $SA$, $SR$ szakaszok hossza $\sqrt[]{5}$, mert mindegyikük egy-egy 1 és 2 egység befogójú derékszögű háromszög átfogója. Az $SP$ pedig $\sqrt[]{3}$ egység hosszú, mert egy egységkocka testátlója. 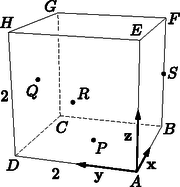  1. ábra  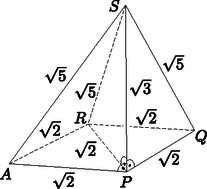 2. ábra Az $RPS$ háromszög derékszögű, mert ${\left(\sqrt[]{2}\right)}^2+{\left(\sqrt[]{3}\right)}^2={\left(\sqrt[]{5}\right)}^2$. Ugyanezért derékszögű az $APS$ és a $QPS$ háromszög is. (Idáig eljuthatunk másként is, lásd az I./$a)$ részmegoldást.) Az $SP$ merőleges az $APQR$ síkra, mert merőleges a sík két egymást metsző egyenesére (a síkra merőleges egyenes tétele), így ez lesz a gúla magassága. Egy $\sqrt[]{2}$ oldalú szabályos háromszög területe: $\begin{array}{c}{\displaystyle t=\frac{{\left(\sqrt[]{2}\right)}^2\sqrt[]{3}}{4}=\frac{\sqrt[]{3}}{2};}\end{array}$ a poliéder térfogata tehát: $\begin{array}{c}{\displaystyle V=\frac{2t\sqrt[]{3}}{3}=\frac{2\frac{\sqrt[]{3}}{2}\sqrt[]{3}}{3}=1\text{ (térfogategység).}}\end{array}$ I./$a)$ részmegoldás. Helyezzük el a kockát egy $\text{x}$, $\text{y}$, $\text{z}$ egységvektorok által meghatározott derékszögű koordinátarendszerben, itt $\overrightarrow{AP}=\text{x}+\text{y}$, $\overrightarrow{AR}=\text{y}+\text{z}$, $\overrightarrow{AQ}=\text{x}+2\text{y}+\text{z}$, $\begin{array}{c}{\displaystyle \overrightarrow{PQ}=\overrightarrow{AQ}-\overrightarrow{AP}=\text{x}+2\text{y}+\text{z}-\left(\text{x}+\text{y}\right)=\text{y}+\text{z}=\overrightarrow{AR}\Rightarrow }\end{array}$ az $APQR$ négyszög paralelogramma, mert két szemközti oldala párhuzamos és egyenlő hosszú. Egy vektor hossza koordinátái négyzetösszegének négyzetgyökével egyenlő, így ${\displaystyle \begin{array}{c}\hfill {\displaystyle |\overrightarrow{AP}|=|\overrightarrow{AR}|=|\overrightarrow{PR}|=|\overrightarrow{PQ}|=|\overrightarrow{RQ}|=\sqrt[]{1^2+1^2}=\sqrt[]{2};}\hfill \\ \hfill {\displaystyle \overrightarrow{PS}=\text{x}-\text{y}+\text{z};|\overrightarrow{PS}|=\sqrt[]{1^2+{\left(-1\right)}^2+1^2}=\sqrt[]{3};}\hfill \\ \hfill {\displaystyle |\overrightarrow{AS}|=|\overrightarrow{RS}|=|\overrightarrow{QS}|=\sqrt[]{1^2+2^2}=\sqrt[]{5}\mathrm{.}}\hfill \end{array}}$ $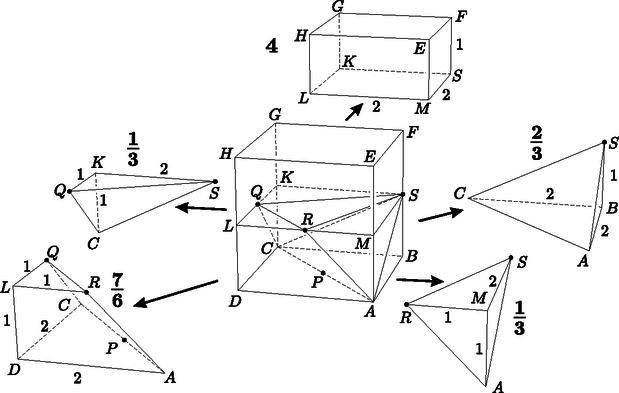a$) II. megoldás. Megkaphatjuk a poliéder térfogatát úgy is, hogy a kockából levágjuk a megfelelő darabokat az ábra szerint.     Az egyes darabok térfogatát a melléjük vastagon írt számok mutatják, ezek kiszámítása triviális. A maradék test térfogata a poliéder térfogatának $\frac{3}{2}$-szerese, mert alapjuk között is ez a viszony áll fenn.     Felírhatjuk, hogy $4+\frac{1}{3}+\frac{1}{3}+\frac{2}{3}+\frac{7}{6}+\frac{3}{2}V=8$. Ebből $V=1$ adódik.   $b)$ Be kell látni, hogy létezik beírt gömb. Az nyilvánvaló, hogy a poliéder szimmetrikus az $RPS$ síkra, ha van érintő gömb, akkor középpontjának ebben a síkban kell lennie. Vegyük az $A$ pontból induló $AP$, $AS$, $AR$ félegyenesek által meghatározott triédert. Síkjainak szögfelező síkjai egy $A$-ból induló, a triéder belsejében haladó félegyenest határoznak meg, mert síkok metszésvonala egyenes, másrészt az egyenlőség tranzitív, tehát, ha az $O$ pont egyenlő távol van az $ASP$ és $ASR$ síkoktól, akkor az $APR$ síktól is ugyanakkora távolságra van.   Ez a félegyenes döfi az $RPS$ síkot, ez az $O$ pont lesz tehát a beírt gömb középpontja. (Szemléletesen ,,indokolható'' a beírt gömb léte úgy is, hogy egy ,,szögletes tölcsérbe'' beleejthetünk egy pingpong labdát, amit aztán megfelelő méretűre ,,fújunk'' fel.) A beírt $r$ sugarú gömb középpontját ($O$) kössük össze a poliéder csúcsaival, így azt az oldallapok alapú, $O$ csúcsú gúlákra daraboltuk fel. Az $ARS$ háromszög olyan egyenlő szárú háromszög, amelynek $AR$ alapja $\sqrt[]{2}$ hosszú, szárai $\sqrt[]{5}$ hosszúak, így az alapjához tartozó $m$ magasságra felírhatjuk: $\begin{array}{c}{\displaystyle {\left(\frac{\sqrt[]{2}}{2}\right)}^2+m^2={\left(\sqrt[]{5}\right)}^2\mathrm{,}\text{ahonnan}m=\frac{3}{\sqrt[]{2}}\mathrm{.}}\end{array}$ Az $APQR$ alapú, $O$ csúcsú gúla térfogata $V_1=\frac{\sqrt[]{3}r}{3}$; az $APS$ alapú, $O$ csúcsú gúla térfogata $\begin{array}{c}{\displaystyle V_2=\frac{\frac{\sqrt[]{2}\sqrt[]{3}}{2}r}{3}=\frac{\sqrt[]{6}}{6}r}\end{array}$ (ekkora a $PQS$ alapú gúláé is); az $ARS$ alapú, $O$ csúcsú gúla térfogata $\begin{array}{c}{\displaystyle V_3=\frac{\frac{\sqrt[]{2}\frac{3}{\sqrt[]{2}}}{2}r}{3}=\frac{1}{2}r}\end{array}$ (egyenlő az $RQS$ alapú gúláéval). Mivel $V_1+2V_2+2V_3=V$; $\begin{array}{c}{\displaystyle \frac{\sqrt[]{3}}{3}r+2\frac{\sqrt[]{6}}{6}r+2\frac{1}{2}r=1;r\left(\frac{\sqrt[]{3}}{3}+\frac{\sqrt[]{6}}{3}+1\right)=1.}\end{array}$ Ebből ${\displaystyle \begin{array}{cc}\hfill {\displaystyle r}& {\displaystyle =\frac{3}{\sqrt[]{3}+\sqrt[]{6}+3}=\text{(két lépésben gyöktelenítve a nevezőt)}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{2\sqrt[]{3}-3\sqrt[]{2}+\sqrt[]{6}}{4}\approx 0\mathrm{,}42.}\hfill \end{array}}$   (Megjegyzés. Minden olyan poliéderre, amelynek van minden lapját érintő beírt gömbje igaz, hogy $\frac{Ar}{3}=V$.)