Kezdőlap


Cím:	Melyik nagyobb az óriások közül?
Szerző(k):	Retkes Zoltan
Füzet:	2019/április, 194 - 200. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Bevezető

2015 májusában, egy kellemesen napsütötte hétvégén meglátogattam a Cambridge-i Egyetem híres matematikai intézetét. Az épületkomplexum leginkább egy marsbéli űrbázist idézett fel bennem, aminek élesen ellentmondani látszott egy csillogó görbét rajzoló csiga és egy kerítésoszlopon érdeklődve szemlélődő mókus. Amint körülsétáltam az épületeket, az egyik süllyesztett szint üvegajtaján keresztül két színes plakát ragadta meg a figyelmem.
Óriások és negatív számozású kocka. A bal oldali plakát kérdéseit kigyűjtöttem alább:

$•$	Melyik nagyobb: $9^{10}$ , vagy $10^{9}$ ?

$•$	Számológéppel eldönthető-e, melyik nagyobb: $99^{100}$ , vagy $100^{99}$ ?

$•$	Döntsük el, hogy $999^{1000}$ , vagy $1000^{999}$ a nagyobb.

Amint hazaértem smallfieldi szobámba, a kíváncsiság nem hagyott, elkezdtem tesztelni a Win10 számológépét. A kalkulátor az 1. ábrán látható válaszokat adta. Az első kérdésben szereplő mennyiségeket ‐ egész aritmetikát használva ‐ gond nélkül kiértékelte. A második és harmadik kérdésben szereplő hatványok kiszámításához normálalakot használt és amikor a

10000^{9999}

hatványt kérdeztem, túlcsordulási hibával leállt. Végül is mindhárom kérdésre választ találtam ‐

9^{10} > 10^{9}

99^{100} > 100^{99}

és

999^{1000} > 1000^{999}

‐, úgyhogy hátradőlhettem volna elégedetten székemben.

1. ábra. Számológépem válaszai

Nem ez történt. Felrémlett egy klasszikus figyelmeztető példa a számelméletből. Az

x^{2} + x + 41

polinom

x = 0,1,2, ...,39

esetén prímszámot eredményez, azonban

40^{2} + 40 + 41 = 40 \cdot 41 + 41 = 41^{2}

, ami nem prím. Szóval attól, hogy tudok valamit az

N = 1,2,3

esetekre, nem lehetek biztos benne, hogy a felismert törvény megmarad nagyobb hatványkitevőkre is. Ahhoz, hogy ezzel a kérdéssel érdemben tudjunk foglalkozni, meg kell alkotnunk a probléma általános matematikai formalizmusát és az eddigi tapasztalatainknak megfelelő sejtést kell bebizonyítanunk. Az általános probléma formálisan a következő:
Legyen

N

pozitív egész és

A_{N} = {(10^{N} - 1)}^{10^{N}}

, valamint

B_{N} = {(10^{N})}^{10^{N} - 1}

. Melyik nagyobb az

A_{N}

és

B_{N}

számok közül? Volt eredetileg három kérdésünk, most pedig végtelen sok lett hirtelen. A matematikai bizonyítás ereje éppen ebben rejlik: egyetlen bizonyítás keretében képes megválaszolni ‐ ebben az esetben ‐ megszámlálhatóan végtelen sok kérdést. Mivel ismerjük a választ az

N = 1,2,3

speciális esetekben, indokoltnak tűnik azt sejteni, hogy

A_{N}

általában is nagyobb, mint

B_{N}

, továbbá vegyük észre, hogy

A_{1} > 3 B_{1}

A_{2} > 30 B_{2}

és

A_{3} > 300 B_{3}

. Most, hogy megalkottuk a pontos matematikai modellt a problémához, az maradt hátra, hogy bizonyítást találjunk sejtésünkre, ami a munka nagyobb, nehezebb és érdekesebb része. A fent megfogalmazott kérdés inspirált egy nagyobb lélegzetvételű munkát, mely teljes egészében a BCME9 2018 (British Congress of Mathematics Education, Warwick University, 3‐6 April 2018, https://www.bcme.org.uk/) konferencián hangzott el. Ezen előadásom anyagából választottam két fejezetet, amik ezen írás gerincét alkotják.

A számjegyek száma

Össze szeretnénk hasonlítani két természetes számot nagyságrendileg. Az egyik legegyszerűbb mód az, ha összehasonlítjuk a számjegyeik számát valamilyen előre lerögzített számrendszerben. Jelen esetben decimális rendszert fogunk használni és a tömörebb leírás érdekében bevezetjük a számjegyek számát megadó függvényt (jelölése

#

). A formális definíció az alábbi:

# : N \to N

# (n) = n

számjegyeinek száma. Például

# (0) = 1

# (9) = 1

és

# (2019) = 4

. Egyszerűen ellenőrizhető a következő alternatív formák érvényessége:

\begin{matrix} # (n) = {max}_{}^{} {k \geq 0 : 10^{k} \leq n} + 1 = {max}_{}^{} {k \geq 0 : k \leq lg (n)} + 1 = ⌊ lg (n) ⌋ + 1. \end{matrix}

Itt és a továbbiakban

lg (.)

a 10-es alapú logaritmust jelöli,

⌊ x ⌋

pedig az

x

valós szám alsó egészrésze, azaz az

x

-nél nem nagyobb egészek közül a legnagyobb. Például

\begin{matrix} # (9^{10}) = ⌊ lg (9^{10}) ⌋ + 1 = ⌊ 10 lg (9) ⌋ + 1 = ⌊ 10 \cdot 0, 954242 ... ⌋ + 1 = 9 + 1 = 10 \end{matrix}

és nyilvánvalóan

# (10^{9}) = 10

. Azt kaptuk, hogy a két szám ugyanolyan hosszú, mindkettő tíz számjeggyel írható fel a decimális rendszerben és mivel a legkisebb ilyen tulajdonságú szám a

10^{9}

, következésképp

9^{10} \geq 10^{9}

. Ugyanakkor

9^{10}

utolsó jegye nem 0, emiatt

9^{10} > 10^{9}

. Az

N = 1

eset fenti elemzése már mutat valamit ezen megközelítés stílusából. Az alábbi összefoglaló táblázatban rögzítettük az

N = 1,2,3

esetekre a számjegyek számát:

\begin{matrix} \begin{matrix} N & 1 & 2 & 3 \\ # (A_{N}) & 10 & 200 & 3000 \\ # (B_{N}) & 10 & 199 & 2998 \end{matrix} \end{matrix}

A táblázatbeli értékek alapján az alábbi tételt tudjuk megfogalmazni:

1. tétel. Legyen

N \geq 1

egész szám,

A_{N} = {(10^{N} - 1)}^{10^{N}}

és

B_{N} = {(10^{N})}^{10^{N} - 1}

. Ekkor minden

N \geq 1

-re a következő egyenlőség áll fenn:

\begin{matrix} # (A_{N}) - # (B_{N}) = N - 1. \end{matrix}

Bizonyítás.
Kezdjük az egyszerűbbel,

B_{N}

számjegyei számának a meghatározásával.

\begin{matrix} # (B_{N}) = # [{(10^{N})}^{10^{N} - 1}] = # [10^{N (10^{N} - 1)}] = N (10^{N} - 1) + 1 = N 10^{N} - (N - 1) \end{matrix}

Ezek alapján elég azt bizonyítani, hogy

# (A_{N}) = N 10^{N}

. Ezt két lépésben tesszük. Az

a)

részben megmutatjuk, hogy

# (A_{N}) \leq N 10^{N}

, ami az egyszerűbb, aztán a

b)

részben a

# (A_{N}) \geq N 10^{N}

egyenlőtlenséget, ami kissé technikásabb.

a)

Induljunk ki a nyilvánvaló

lg (10^{N} - 1) < N

egyenlőtlenségből, amit

10^{N}

-nel szorozva

10^{N} lg (10^{N} - 1) < N 10^{N}

, azonban

10^{N} lg (10^{N} - 1) = lg [{(10^{N} - 1)}^{10^{N}}] = lg (A_{N})

, így

⌊ lg (A_{N}) ⌋ \leq N 10^{N} - 1

, ahonnan

# (A_{N}) = ⌊ lg (A_{N}) ⌋ + 1 \leq N 10^{N}

b)

Elegendő megmutatni, hogy

\begin{matrix} 10^{N} lg (10^{N} - 1) > N 10^{N} - 1. \end{matrix}

(1)

Először belátjuk, hogy (1) ekvivalens a következővel:

\begin{matrix} lg [{(1 + \frac{1}{10^{N} - 1})}^{10^{N} - 1}] < 1 - \frac{1}{10^{N}} . \end{matrix}

(2)

Ehhez helyettesítsünk

\begin{matrix} lg (10^{N} - 1) = lg [10^{N} (1 - \frac{1}{10^{N}})] = N + lg (1 - \frac{1}{10^{N}}) -t \end{matrix}

(1)-be és egyszerűsítsünk a mindkét oldalon fellépő

N 10^{N}

taggal. Így:

\begin{matrix} 10^{N} lg (1 - \frac{1}{10^{N}}) > - 1 \Leftrightarrow - lg (1 - \frac{1}{10^{N}}) = lg (1 + \frac{1}{10^{N} - 1}) < \frac{1}{10^{N}}, \end{matrix}

amit

(10^{N} - 1)

-gyel szorozva kapjuk (2)-t. Az

e

szám tárgyalásakor mindenki találkozik a következő, ismertnek feltételezett egyenlőtlenséggel:

(1 + \frac{1}{k})^{k} < 3

minden

k \geq 1

esetén. Alkalmazzuk most ezt

k = 10^{N} - 1

-re, ahonnan

\begin{matrix} lg [{(1 + \frac{1}{10^{N} - 1})}^{10^{N} - 1}] < lg (3) \approx 0.4771 < \frac{1}{2} < 1 - \frac{1}{10^{N}} (\forall N \geq 1), \end{matrix}

így (1) fennáll és következésképp

\begin{matrix} # (A_{N}) = ⌊ 10^{N} lg (10^{N} - 1) ⌋ + 1 \geq N 10^{N}, \end{matrix}

amit bizonyítani szerettünk volna.

□

A fenti tétel birtokában és emlékezve az

N = 1

speciális esetre kapott eredményre, válaszunk a végtelen sok esetre röviden:

A_{N} > B_{N} \forall N \geq 1

A hiperkocka

Mielőtt rátérnénk a fejezetcímben szereplő geometriai modell elemzésére, vegyük észre, hogy az eredeti kérdés értelmes hatványok egy sokkal bővebb halmazára: nevezetesen minden természetes számra megkérdezhetjük, hogy vajon

n^{n + 1}

, vagy pedig

{(n + 1)}^{n}

a nagyobb. Az előző fejezetben

n = 10^{N} - 1

alakú számokra válaszoltuk meg a kérdést. Az alábbi táblázatból a következőt tudjuk kiolvasni:

n = 1,2

esetén

n^{n + 1} < {(n + 1)}^{n}

, az

n = 3,4,5,6

értékekre pedig

n^{n + 1} > {(n + 1)}^{n}

\begin{matrix} \begin{matrix} n & 1 & 2 & 3 & 4 & 5 & 6 \\ n^{n + 1} & 1 & 8 & 81 & 1024 & 15625 & 279936 \\ {(n + 1)}^{n} & 2 & 9 & 64 & 625 & 7776 & 117649 \end{matrix} \end{matrix}

A továbbiakban azt fogjuk bizonyítani, hogy

n^{n + 1} > {(n + 1)}^{n} \forall n \geq 3

, felépítve egy érdekes geometriai kapcsolatot az egyenlőtlenségben szereplő hatványok és az

(n + 1)

élhosszúságú

n

dimenziós hiperkocka egy speciális partíciója között. Először elvégezzük a bizonyítást

n = 3

dimenzióra, majd az itt szerzett tapasztalatokat átültetjük

R^{n}

-be. Azt szeretnénk belátni, hogy

3^{4} > 4^{3}

. Egy pillanatra tekintsünk el attól, hogy nyilvánvalóan mindenki tudja, hogy

3^{4} = 81 > 64 = 4^{3}

. Tekintsünk az egyenlőtlenségre a következő módon:

3 \cdot 3^{3} > 4^{3}

és interpretáljuk a

4^{3}

mennyiséget mint a

(0,0,0)

és

(4,4,4) \in R^{3}

átellenes csúcspontok által kifeszített

4

egység élhosszúságú kocka térfogatát.
Ebben az értelmezésben az egyenlőtlenség azt mondja, hogy ez a kocka összerakható

3

3 \times 3 \times 3

-as kockát alkotó, összesen

3 \times 27

egységkockából úgy, hogy legalább egy közülük felesleges (szigorú egyenlőtlenség). A továbbiakban minden előforduló kockát és téglatestet úgy tekintünk, hogy egységkockákból összeragasztással keletkezik. Szét tudjuk őket szedni és más formában újra összerakni.

2. ábra. Kocka reprezentáció 3D

A 2. ábrán (mely a borítón színesben látható) világosan lehet követni, ahogyan a kiindulási

4 \times 4 \times 4

-es kocka felépíthető egy

3 \times 3 \times 3

-as (kék) kockából; 3 db

3 \times 3 \times 1

-es (piros) téglatest ad egy másik

3 \times 3 \times 3

-as kockát; és végül maradt 3db

3 \times 1 \times 1

-es (zöld) tégla valamint egy

1 \times 1 \times 1

-es (lila) sarok kocka, amik együttesen (10) kevesebb egységkockát tartalmaznak, mint a harmadik

3 \times 3 \times 3

-as kocka (27). Ez a konstrukció valóban azt mutatja, hogy

3^{4} = 3 \cdot 3^{3} > 4^{3}

. Könnyen követhető, hogy mi történik, amint az alkotórészeket összerakjuk. Először felhasználunk

27

egységkockát (kék), majd

3 \cdot 9 = 27

egységkockát (piros) és még szükségünk van

3 \cdot 3 = 9

(zöld) plusz 1 (lila) egységkockára.

27 + 3 \cdot 9 + 3 \cdot 3 + 1 = 64

. Vegyük észre azt is, hogy a beépített alkotórészek száma

1,3,3,1

. Ez könnyen eszünkbe juttathatja a Pascal-háromszög harmadik sorát és a binomiális tételt. Ahhoz, hogy a fenti módszert általánosítani tudjuk, néhány előkészületre lesz szükségünk. Bevezetjük a következő jelöléseket:

$•$	$x^{i}$ az $i$ -edik koordinátatengely $R^{n}$ -ben.

$•$	$n^{i} = {[0, n)}^{i}$ és $1^{i} = {[n, n + 1]}^{i}$ , ahol az $i$ index arra utal, hogy a szóbanforgó intervallumok az $i$ -edik tengelyen, $x^{i}$ -n vannak.

$•$	$a (w) = a w$ szimbólum előfordulásainak száma egy kifejezésben; például ha $e = w \times n \times w$ , akkor $a (w) = 2$ és $a (n) = 1$ . Az $a (.)$ függvény használatakor részletezni fogjuk, hogy pontosan mit is számol az adott helyzetben.

$•$	Legyen $A \subseteq R^{n}$ egy mérhető részhalmaz, $Vol (A)$ az $A$ térfogata.

$•$	$\times_{j = 1}^{m} A_{j}$ az $A_{j}$ részhalmazok Descartes-szorzata.

•

3^{x} \oplus 1^{x} = 4^{x}

jelentése:

3^{x} = {[0,3)}^{x}

-hez ragasztjuk az

1^{x} = {[3,4]}^{x}

egységintervallumot, ami így a

{[0,4]}^{x}

-t eredményezi; 3D-ben a szokásos

x, y, z

tengelyreferenciát fogjuk használni. Nyilvánvalóan érvényesek az

A \oplus B = B \oplus A

és

A \times (B \oplus C) = (A \times B) \oplus (A \times C)

azonosságok (3. ábra)

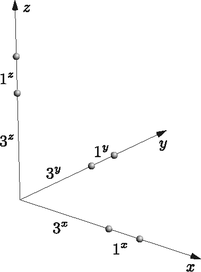3. ábra. Intervallumok 3D-ben

Az eddig leírtakat a fenti fogalmakkal és műveletekkel lehet elegáns matematikai formába önteni. A 3. ábrán szereplő intervallumok Descartes-szorzataival elő tudjuk állítani a 2. ábrán látható alkotórészeket. Kezdjünk megint a 3D esettel. Jelölje

C_{3}

[0,4] \times [0,4] \times [0,4]

kockát. Ekkor

\begin{matrix} C_{3} & = & \times_{i = 1}^{3} (3^{i} \oplus 1^{i}) = (3^{x} \oplus 1^{x}) \times (3^{y} \oplus 1^{y}) \times (3^{z} \oplus 1^{z}) = \\ = & {\overset{}{\overset{︷}{(3^{x} \times 3^{y} \times 3^{z})}}}_{}^{kék} \oplus \\ \oplus {\overset{}{\overset{︷}{(3^{x} \times 3^{y} \times 1^{z})}}}_{}^{piros} \oplus {\overset{}{\overset{︷}{(3^{x} \times 1^{y} \times 3^{z})}}}_{}^{piros} \oplus {\overset{}{\overset{︷}{(1^{x} \times 3^{y} \times 3^{z})}}}_{}^{piros} \oplus \\ \oplus {\overset{}{\overset{︷}{(3^{x} \times 1^{y} \times 1^{z})}}}_{}^{zöld} \oplus {\overset{}{\overset{︷}{(1^{x} \times 3^{y} \times 1^{z})}}}_{}^{zöld} \oplus {\overset{}{\overset{︷}{(1^{x} \times 1^{y} \times 3^{z})}}}_{}^{zöld} \oplus \\ \oplus {\overset{}{\overset{︷}{(1^{x} \times 1^{y} \times 1^{z})}}}_{}^{lila} . \end{matrix}

Legyen most

n \geq 3

tetszőleges és

C_{n}

jelölje az

n

dimenziós hiperkockát, melyet a

(0,0, ...,0)

és

(n + 1, n + 1, ..., n + 1)

pontok feszítenek ki. Ekkor ezen kocka térfogatára:

\begin{matrix} {(n + 1)}^{n} = Vol (C_{n}) = Vol [\times_{i = 1}^{n} (n^{i} \oplus 1^{i})] = Vol [\oplus_{u \in {n,1}} (u^{1} \times u^{2} \times \dots \times u^{n})] = \\ = Vol [\oplus_{k = 0}^{n} \oplus_{u \in {n,1} a (1) = k} (u^{1} \times u^{2} \times \dots \times u^{n})] = \sum_{k = 0}^{n} Vol [\oplus_{u \in {n,1} a (1) = k} (u^{1} \times u^{2} \times \dots \times u^{n})] . \end{matrix}

A fenti és a további formulákban az összeragasztási műveletre bevezetett

\oplus

alatti

a (1) = k

u

formális változó helyettesítésekor előforduló

1

-esek számát adja, ami itt éppen

k

. Ahhoz, hogy használható felső becslést tudjunk adni, vegyük észre a következőket:

a)

k = 0,1, ..., n - 2

, akkor

\begin{matrix} Vol [\oplus_{u \in {n,1} a (1) = k} (u^{1} \times u^{2} \times \dots \times u^{n})] & = \sum_{1 \leq i_{1} < ... < i_{k} \leq n} n^{n - k} \leq \sum_{1 \leq i_{1} \leq ... \leq i_{k} \leq n} n^{n - k} = \\ = n^{k} \times n^{n - k} = n^{n} . \end{matrix}

b)

k = n - 1

és

k = n

indexekre

\begin{matrix} (\binom{n}{n - 1}) \cdot n^{1} + (\binom{n}{n}) \cdot n^{0} = n^{2} + 1 < n^{n} ha n \geq 3, \end{matrix}

következésképpen az alábbi becslést kapjuk:

\begin{matrix} {(n + 1)}^{n} < (n - 1) \cdot n^{n} + n^{n} = n \cdot n^{n} = n^{n + 1} . \end{matrix}

Emlékeztetőül: az

n = 3

esetre vázolt bizonyítás végén megjegyeztük, hogy a

4 \times 4 \times 4

-es kocka partíciójában szereplő alkotórészek darabszámai 1, 3, 3, 1, a Pascal-háromszög

3

. sora. Hol szerepelnek a binomiális együtthatók az

n

-dimenziós esetben? Tudunk valamit mondani az

n^{n + 1} / {(n + 1)}^{n}

hányadosról? Ezekre a kérdésekre keresünk választ a hátralévő részben. Mivel

(\binom{n}{k})

-féleképpen tudunk

k

indexet kiválasztani az

{1,2, ..., n}

halmazból, így egyrészt

\begin{matrix} \sum_{1 \leq i_{1} < ... < i_{k} \leq n}^{} n^{n - k} = (\binom{n}{k}) n^{n - k}, \end{matrix}

ami azt mutatja, hogy a fenti bizonyítás ekvivalens az

{(n + 1)}^{n}

binomiális tétel szerinti kifejtésével. Másrészről a következő felső becslés adható:

\begin{matrix} (\binom{n}{k}) n^{n - k} = \frac{n (n - 1) \dots (n - k + 1)}{k!} n^{n - k} \leq \frac{1}{k!} n^{k} n^{n - k} = \frac{1}{k!} n^{n} . \end{matrix}

Innen azt kapjuk, hogy

\begin{matrix} {(n + 1)}^{n} = \sum_{k = 0}^{n} (\binom{n}{k}) n^{n - k} \leq (\sum_{k = 0}^{n} \frac{1}{k!}) n^{n} < e n^{n} < 3 n^{n}, \end{matrix}

ahonnan végül az alábbi becslés nyerhető:

\begin{matrix} \frac{n}{3} < \frac{n}{e} < \frac{n}{s_{n}} < \frac{n^{n + 1}}{{(n + 1)}^{n}}, \end{matrix}

ahol

s_{n}

\sum_{k = 0}^{\infty} \frac{1}{k!}

sor

n

-edik részletösszegét jelöli.
Visszatérve egy pillanatra az eredeti kérdéshez, a fenti becslés alapján az

n = 10 - 1 = 9

10^{2} - 1 = 99

10^{3} - 1 = 999

értékekre

9^{10}

99^{100}

999^{1000}

rendre legalább

3,33,333

-szor nagyobb, mint

10^{9}

100^{99}

1000^{999}

. A pontos hányadosok 4 tizedesjegyre kerekítve 3,4867, 36,6032, 367,6954. Az

e

számot használó becslésre a faktorok: 3,3109, 36,4201, 367,5116. Ez a becslés igen pontos abban az értelemben, hogy

⌊ \frac{n}{e} ⌋ = ⌊ \frac{n^{n + 1}}{{(n + 1)}^{n}} ⌋

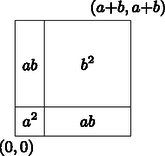4. ábra. Az

n = 2

dimenziós hiperkocka partíciója

A hiperkocka modell egy másik előnye, hogy a fenti gondolatmenet mentén a

(0,0, ...,0)

(a + b, a + b, ..., a + b)

szemközti csúcsokkal rendelkező hiperkockát partícionálva a binomiális tétel geometriai bizonyítása nyerhető és az azonos típusú alkotórészek száma éppen a Pascal-háromszög egy sorában található binomiális együtthatókkal egyezik meg.

Zoltan Retkes
26, Moore Road, Barwell, UK
e-mail: tigris35711@gmail.com