Cím:	A 2019. évi Kunfalvi Rezső olimpiai válogatóverseny elméleti feladatai
Füzet:	2019/április, 233 - 238. oldal	PDF  |  MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   A 2019. évi Kunfalvi Rezső olimpiai válogatóverseny elméleti feladatai${}^1$   1. Buborékok képződése és mozgása pezsgőben Szilveszteri koccintáskor megfigyelhetjük, hogy a pezsgőben buborékfonalak alakulnak ki, azaz a buborékok a pohár aljának vagy oldalfalának bizonyos pontjairól indulva libasorban emelkednek a felszín felé. A buborékok képződésének oka, hogy a pezsgő előállításakor az italt nagy (2-5 atmoszféra) nyomás alatt szén-dioxiddal telítik, ami légköri nyomáson túltelített oldatot eredményez, így a CO${}_2$ gáz formájában fokozatosan kiválik a folyadékból. Ez a kiválás a pohár belső falának mikroszkopikus egyenetlenségeinél, szennyeződéseinél történik meg legnagyobb valószínűséggel, ezek az ún. nukleációs magvak. Ha egy buborékkezdemény már kialakult, akkor a gáz-folyadék határfelületen tovább folytatódik a CO${}_2$ kiválása egészen addig, amíg a buborék olyan nagyra hízik, hogy nagy része leválik a magról. Ekkor csak egy apró buborékkezdeményt hagy maga után, amely szintén növekedésnek indul.1 Ebben a feladatban a buborékok leválásának és emelkedő mozgásának leírásával foglalkozunk egy olyan egyszerű modell segítségével, amely bizonyos feltételek mellett a részletes számolások és kísérletek szerint is jól közelíti a valóságot.   1.A. Buborékok képződése és leválása Tegyük fel, hogy a pohár alján lévő egyik nukleációs mag egy kicsiny, $b$ sugarú, kör alakú bemélyedés, amelyen lassan egy buborék fejlődik (1. ábra). Egy adott pillanatban a buborék térfogata $V$, magassága $h$, görbületi sugara a legfelső pontjában $r_{\text{g}}$, illeszkedési szöge a pohár aljához képest $\theta$. A folyadék nyomása közvetlenül a buborék tetejénél $p$. A buborékra a folyadék hidrosztatikai nyomásától származó $F_1$ erő, a bezárt CO${}_2$-gáz nyomásából származó $F_2$ erő, illetve a bemélyedésnél ható, felületi feszültségből származó $F_3$ erő h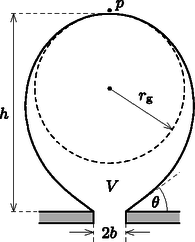at.   1. ábra   1.A.1. Fejezzük ki az $F_1$ erőt a folyadék (pezsgő) $\varrho$ sűrűsége, a $g$ nehézségi gyorsulás, valamint az 1. ábrán feltüntetett mennyiségek segítségével! 1.A.2. Fejezzük ki az $F_2$ erőt a folyadék $\sigma$ felületi feszültsége és az 1. ábrán látható mennyiségek segítségével! 1.A.3. Adjuk meg az $F_3$ erőt a $\sigma$ felületi feszültség és az 1. ábrán látható paraméterek segítségével! 1.A.4. Az előző alkérdésekre kapott eredmények felhasználásával írjuk fel a buborék egyensúlyát kifejező egyenletet! A buborék alakját a hidrosztatikai nyomásból és a felületi feszültségből származó erők együttesen határozzák meg. Ha a buborék mérete sokkal kisebb egy bizonyos $\kappa$ hosszúságnál, akkor a buborék nagy része (egy vékony ,,nyaktól'' eltekintve) jó közelítéssel gömb alakú marad még a nukleációs magról való leszakadáskor is, ahogy az a 2. ábra első négy rajzán látható. 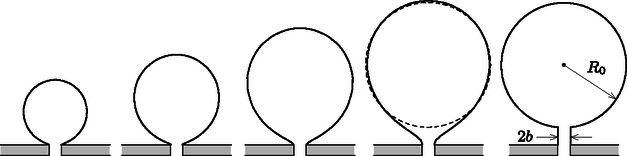    2. ábra   1.A.5. Adjunk becslést $\kappa$ értékére a pezsgő $\varrho$ sűrűsége, a $g$ nehézségi gyorsulás és a $\sigma$ feszültség segítségével! (Feltehetjük, hogy a ${\text{CO}}_2$ gáz sűrűsége jóval kisebb a folyadék sűrűségénél.) A továbbiakban tegyük fel, hogy a buborék mérete sokkal kisebb, mint $\kappa$! Ekkor a buborék alakja a leválás pillanatában egy $R_0$ sugarú gömbbel és a hozzá csatlakozó $b$ sugarú, henger alakú, vékony ($b\ll R_0$), rövid nyakkal modellezhető (lásd a 2. ábra utolsó rajzát). 1.A.6. Fejezzük ki a bemélyedés (és a buborék nyakának) $b$ sugarát az éppen leváló buborék $R_0$ sugara, valamint $\varrho$, $g$ és $\sigma$ segítségével! Használjuk fel, hogy ${\left(1+\epsilon \right)}^n\approx 1+n\epsilon$, ha $|\epsilon |\ll 1$. 1.A.7. Számítsuk ki az éppen leváló buborék $R_0$ sugarát, ha $\varrho ={10}^3\text{kg}/{\text{m}}^3$, $g=9\mathrm{,}8{\text{m/s}}^2$, $\sigma =50\text{mN/m}$ és $b=0\mathrm{,}5\mu \text{m}$.   1.B. Buborékok felszálló mozgásának leírása A buborék belsejében lévő szén-dioxid mennyisége a nukleációs magról történő leválás után tovább növekszik. Ennek üteme jó közelítéssel arányos a buborék falának $A$ felszínével: $\begin{array}{c}{\displaystyle \frac{\Delta N}{\Delta t}=\gamma A\mathrm{,}}\end{array}$ ahol $\gamma$ egy állandó, $\Delta N$ pedig a kicsiny $\Delta t$ idő alatt a folyadékból kiváló CO${}_2$-molekulák száma. A feladat következő részében tételezzük fel, hogy a pezsgő (és a benne lévő buborék) hőmérséklete mindvégig az ideális $T=15{}^{\circ }$C, a buborék jó közelítéssel gömb alakú marad, a légköri nyomás értéke pedig $p_0={10}^5$ Pa. 1.B.1. Adjuk meg a buborék $R\left(t\right)$ sugarát a leválás után $t$ idő elteltével $R_0$, $\gamma$, $T$, $p_0$ és univerzális állandó(k) felhasználásával! A felfelé mozgó buborékra a hidrosztatikai felhajtóerő és a $v$ sebességgel arányos nagyságú ún. Stokes-féle közegellenállási erő hat: $F_{\text{Stokes}}=6\pi R\eta v$, ahol $R$ a buborék pillanatnyi sugara, $\eta$ pedig a folyadék belső súrlódását jellemző ún. viszkozitás. 1.B.2. Adjuk meg a buborék $v\left(t\right)$ sebességét a leválás után $t$ idő elteltével $R_0$, $\gamma$, $T$, $p_0$, $\varrho$, $g$, $\eta$ és univerzális állandó(k) felhasználásával! A pohárban $H=10$ cm magasan áll a pezsgő. A pohár aljáról induló buborék $t_0=1\mathrm{,}2$ s alatt éri el a felszínt. A pezsgő viszkozitása $\eta =1\mathrm{,}6\cdot {10}^{-3}\text{Pa}\cdot \text{s}$. Ha az 1.A.7. alkérdésben nem sikerült meghatározni a leváló buborék $R_0$ sugarát, akkor azt vegyük $R_0=0\mathrm{,}16$ mm-nek! 1.B.3. Mekkora a buborék $R\left(t_0\right)$ sugara, amikor eléri a felszínt? Adjuk meg a sugár számszerű értékét is! Matematikai segítség: Szükségünk lehet a következő integrálra: $\begin{array}{c}{\displaystyle \int {\left(a+bx\right)}^n\text{d}x=\frac{{\left(a+bx\right)}^{n+1}}{b\left(n+1\right)}+\text{konstans}\mathrm{.}}\end{array}$   2. Ponttöltés mozgása oszcilláló elektromos térben Egy gömbkondenzátor két koncentrikus, $R$ és $2R$ sugarú, igen jól vezető fémgömbhéjből áll; a gömbök közötti térben vákuum van. A kondenzátor fegyverzetei közé egy váltóáramú feszültségforrást helyezünk, amit egy-egy sugárirányú, egyenes vezetékkel csatlakoztatunk a gömbökhöz (3. ábra). A gömbökre kapcsolt feszültség $U\left(t\right)=U_0\text{cos}\omega t$ módon változik az idő függvényében. 2.1. Határozzuk meg a gömbkondenzátor kapacitását! A választ $R$ és univerzális állandó(k) segítségével adjuk meg! 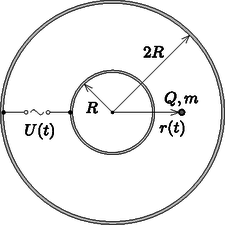  3. ábra   Ha a váltakozó feszültség körfrekvenciája nem túl magas, a kondenzátor feszültsége (az igen jól vezető gömbök miatt) ,,követi'' a feszültségforrást, a fáziskésés lényegében zérus (ez a kvázisztatikus eset). Ha azonban a váltakozó feszültség $\omega$ körfrekvenciája megközelít egy bizonyos ${\omega }_1$ értéket, akkor a rendszer induktív ellenállása számottevő lesz, így a kvázisztatikus közelítés nem alkalmazható. 2.2. Adjunk nagyságrendi becslést ${\omega }_1$ értékére, ha $R=10$ cm. Ismert továbbá, hogy a vákuum dielektromos állandója ${\epsilon }_0=8\mathrm{,}85\cdot {10}^{-12}{\text{C}}^2/\left({\text{Nm}}^2\right)$, permeabilitása ${\mu }_0=4\pi \cdot {10}^{-7}\text{Vs}/\left(\text{Am}\right)\mathrm{.}$ A továbbiakban tegyük fel, hogy $\omega \ll {\omega }_1$! A gömbök közötti térben, a feszültségforrással átellenes oldalon egy $+Q$ töltésű, $m$ tömegű kis porszem található. Feltételezhetjük, hogy a porszemre ható nehézségi erő hatása a feladat során végig elhanyagolható. Jelöljük a porszem gömbök középpontjától mért távolságát $r$-rel! Ha a váltakozó feszültség körfrekvenciája sokkal nagyobb egy bizonyos ${\omega }_2$ értéknél, akkor a gyöngy mozgása felbontható egy lassú, sodródó mozgásra és egy akörül gyorsan oszcilláló, kis $A\left(t\right)$ amplitúdójú rezgőmozgásra: $r\left(t\right)=r_0\left(t\right)+A\left(t\right)\text{cos}\omega t$, ahol $A\left(t\right)\ll r_0\left(t\right)$, valamint $A\left(t\right)$ és $r_0\left(t\right)$ lassan változó függvények. Ez azt jelenti, hogy teljesülnek az ${\mathrm{<mover\; accent="true">r<mo>¨</mo></mover>}}_0\left(t\right)$, $Ä\left(t\right)$, $\dot{A}\left(t\right)\omega \ll A\left(t\right){\omega }^2$ relációk (a mennyiség fölé tett pont és kettőspont az első és második idő szerinti deriváltat jelöli). 2.3. Adjunk nagyságrendi becslést ${\omega }_2$ értékére $m$, $Q$, $R$ és $U_0$ segítségével! Számítsuk ki ${\omega }_2$ becsült értékét $R=10$ cm, $m={10}^{-16}$ kg, $Q=1\mathrm{,}6\cdot {10}^{-12}$ C, $U_0=1\mathrm{,}0$ V esetén! A következő feladatokban tegyük fel, hogy ${\omega }_2\ll \omega \ll {\omega }_1$! A porszem gyorsulása az $\begin{array}{c}{\displaystyle \mathrm{<mover\; accent="true">r<mo>¨</mo></mover>}\left(t\right)=\frac{\alpha }{r{\left(t\right)}^2}\text{cos}\omega t}\end{array}$ (2.1) egyenlet szerint változik az idő függvényében, ahol $\alpha$ állandó paraméter. 2.4. Fejezzük ki az $\alpha$ paraméter értékét $m$, $Q$, $R$ és $U_0$ segítségével! 2.5. Az említett közelítések segítségével adjuk meg a gyors oszcilláció $A\left(t\right)$ amplitúdóját $\alpha$, $r_0\left(t\right)$ és $\omega$ felhasználásával! A $\left(2.1\right)$ egyenlet egy periódusidőre vett átlagolásával összefüggést állapíthatunk meg a porszem lassú, sodródó mozgását leíró $r_0\left(t\right)$ függvény és annak ${\mathrm{<mover\; accent="true">r<mo>¨</mo></mover>}}_0\left(t\right)$ gyorsulása között. A lassan változó mennyiségek ‐ $A\left(t\right)$ és $r_0\left(t\right)$ ‐ egy periódus alatt alig változnak, így az időátlagolás során állandónak vehetők. 2.6. Az eddig használt közelítéseket és a 2.5. alkérdés eredményét felhasználva fejezzük ki a lassan sodródó mozgás ${\mathrm{<mover\; accent="true">r<mo>¨</mo></mover>}}_0\left(t\right)$ gyorsulását $r_0\left(t\right)$, $\alpha$ és $\omega$ segítségével! 2.7. Feltételezve, hogy a $t=0$ időpillanatban a porszem a kisebb fémgömb felületének közeléből indult, határozzuk meg, mekkora sodródási sebességgel ér el a porszem a nagyobb gömbhöz! Az eredményt $m$, $Q$, $R$, $U_0$ és $\omega$ segítségével adjuk meg! Matematikai segítség: Szükségünk lehet a következő integrálra: $\begin{array}{c}{\displaystyle \int x^n\text{d}x=\frac{x^{n+1}}{n+1}+\text{konstans}\mathrm{.}}\end{array}$ 2.8. Adjuk meg a porszem sodródási sebességének számszerű értékét akkor, amikor eléri a nagy gömböt! Legyen $\omega =2\cdot {10}^5$ 1/s, $R=10$ cm, $m={10}^{-16}$ kg, $Q=1\mathrm{,}6\cdot {10}^{-12}$ C, $U_0=1\mathrm{,}0$ V!   3. Száloptikás giroszkóp A mechanikus giroszkóp a pörgettyű elvén működő eszköz, amelynek lelke egy olyan lendkerék, amelynek szimmetriatengelye a háromtengelyű felfüggesztésnek köszönhetően szabadon el tud fordulni. A felpörgetett kerék a perdületmegmaradás miatt a felfüggesztés mozgatásakor is megőrzi eredeti forgástengelyét, így alkalmas irányok megtartására és szögsebességmérésre is. A száloptikás giroszkóp csak a felhasználási módjában hasonlít a mechanikus giroszkópra, hiszen ez is alkalmas egy forgó koordináta-rendszer szögsebességének meghatározására. Az eszköz lényegében egy ún. Sagnac-féle interferométer száloptikás változata, amelyben az interferáló fényhullámok fáziskülönbsége függ a koordináta-rendszerrel együtt forgó eszköz szögsebességétől. Ez a feladat a száloptikás giroszkóp működési elvével foglalkozik.   3.A. A Sagnac-féle interferométer A Sagnac-féle interferométer egyik változatát a 4. ábra mutatja. Ez az eszköz két ideális síktükörből és egy nyalábosztóból áll, amelyek egy $L$ oldalú szabályos háromszög alakjában vannak elrendezve. A nyalábosztóra ${60}^{\circ }$-os beesési szögben $I_0$ intenzitású, $\lambda$ hullámhosszúságú monokromatikus síkhullám esik a fényforrásból. A nyalábosztó egy dielektromos (szigetelő) anyagból készült vékony plánparallel lemez, amelynek felső lapja féligáteresztő tükörként viselkedik, azaz a rá eső fény intenzitásának felét visszaveri, másik felét pedig átengedi. A nyalábosztó alsó lapja egy vékony bevonatnak köszönhetően nem tükröző. 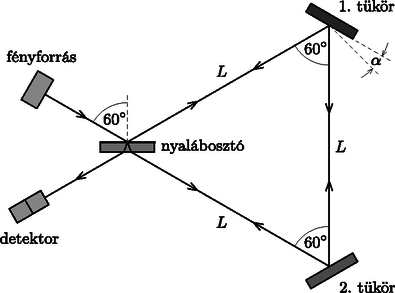    4. ábra   A nyalábosztón való áthaladás után a fény az óramutató járásával megegyező, és azzal ellentétes irányban is végigpattog a tükrökön, míg végül mindkét hullám újra a nyalábosztóhoz érkezik. Itt a hullámok ismét kettéválnak fele-fele intenzitásarányban, így a hullámok egy része a fényforrásba visszajutva egyesül, másik része pedig (egymással interferálva) a detektorba jut. 3.A.1. Az interferométer alaphelyzetében mekkora intenzitást mér a detektor, és mekkora intenzitású fény jut vissza a fényforrásba? 3.A.2. Az interferométer 1. tükrét kicsiny $\alpha$ szöggel elforgatjuk a 4. ábrán látható módon. Változik-e, és ha igen, hogyan változik a detektor által mért intenzitás $\alpha$ függvényében?   3.B. A száloptikás Sagnac-féle interferométer, mint giroszkóp A 4. ábrán bemutatott interferométert optikai szálak segítségével is meg lehet valósítani (5. ábra). Az optikai szálak fényvezető magjának törésmutatójáról tételezzük fel, hogy 1-hez közeli érték. A használt fény hullámhossza $\lambda$, a fényforrásból kiinduló intenzitás a szálban $I_0$. Az egyenlő intenzitású nyalábosztást két optikai szál közötti csatolással valósítják meg: ha a két szál fényvezető magja elég közel helyezkedik el egymáshoz, az elektromágneses hullám ,,átcsatolódhat'' az egyik szálból a másikba. Ha a csatoláshoz egy bejövő hullám érkezik, akkor a két továbbhaladó hullám egymáshoz viszonyított fáziskülönbsége $\pi /2$ lesz. A fényforrás felől érkező nyaláb két fele az óramutató járásával azonos ($-$), illetve azzal ellentétes ($+$) irányban halad végig $N$ darab, egyenként $A$ területű hurkon, míg a csatoláson újra áthaladva a detektorba, valamint a fényforrásba jut. 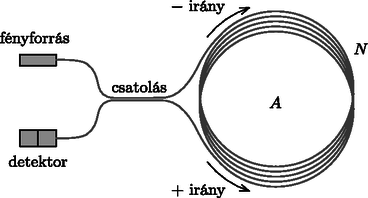    5. ábra   Ha az 5. ábrán látható interferométert a kör alakú hurkok középpontja körül $\Omega$ szögsebességgel megforgatjuk, akkor a $+$ és $-$ irányba haladó hullámok hullámhossza a Doppler-effektus miatt kicsit megváltozik. Így a detektor által mért intenzitás $\Omega$ függvénye lesz. 3.B.1. Határozzuk meg a $+$ és $-$ irányba terjedő hullámok $\varphi$ fáziskülönbségét, amikor a detektorba érnek! A választ $\lambda$, $A$, $N$ és $\Omega$ univerzális állandó(k) segítségével adjuk meg! 3.B.2. Adjuk meg a detektor által mért intenzitást a $+$ és $-$ irányba terjedő hullámok $\varphi$ fáziskülönbsége és $I_0$ segítségével! 3.B.3. Egy tipikus száloptikás giroszkópban $200$ m hosszú optikai szál van feltekerve egy $d=10$ cm átmérőjű, függőleges tengelyű csévetestre. Mekkora fáziskülönbséget mérhetünk a két nyaláb között Budapesten a Föld forgása miatt? (Budapest földrajzi szélessége kb. ${47}^{\circ }$.) 1A versenyt a nemzetközi diákolimpiához hasonló körülmények között Budapesten rendezték meg 2019 márciusában. A feladatokat Vigh Máté állította össze.