Beszámoló a 2018. évi Eötvös-versenyről

 

I. megoldás (energiaminimum). Ha nem forogna a henger, a buborék a felületi feszültség miatt gömb alakú lenne. Ha nem lenne felületi feszültség, akkor a forgó folyadékban a buborék egy nagyon hosszan elnyúló nagyon vékony szál lenne a henger szimmetriatengelyénél. Most a henger elég nagy szögsebességgel forog, de hat a felületi feszültség is, így egy hosszan elnyúlt ,,virsli'' alakú buborékot feltételezünk, melynek alakját egy $r$ sugarú, $\ell$ hosszúságú hengerrel közelíthetjük. A térfogat állandósága miatt $\ell r^2\pi =V$.
A rendszer teljes energiája a buborék felületi energiájából és a buborék helyéről kiszoruló folyadék helyzeti energiájából adódik össze. Akkor lesz egyensúly, ha ez az energia minimális.
A forgó rendszerben egy $\text{d}m$ tömegű folyadékdarabra a henger tengelyétől $x$ távolságra ${\omega }^{2}x\text{d}m$ centrifugális erő hat. Emiatt a henger tengelyétől $x$ távolságra lévő tömegdarab helyzeti energiája

$\begin{array}{c}{\displaystyle \text{d}E=-\underset{0}{\overset{x}{\int }}{\omega }^{2}x\text{'}\text{d}m\text{d}x\text{'}=-\frac{1}{2}{\omega }^2{x}^2\text{d}m\mathrm{.}}\end{array}$

A henger alakú buborékból kiszorul a víz, és a henger szimmetriatengelyéig ,,emelkedik''. A teljes helyzeti energia növekedése, felhasználva, hogy az $x$ sugarú, $\text{d}x$ vastagságú ,,hengergyűrű'' tömege $\text{d}m=\varrho 2x\pi \ell \text{d}x$,

$\begin{array}{c}{\displaystyle E_{\text{cf}}=\underset{0}{\overset{r}{\int }}\frac{1}{2}{\omega }^2{x}^2\varrho \cdot 2x\pi \ell \text{d}x=\frac{1}{4}{\omega }^2{r}^4\varrho \ell \pi =\frac{1}{4}{\omega }^2{r}^2\varrho V\mathrm{.}}\end{array}$

A felületi energia (a henger ismeretlen alakú végeinek járulékát elhanyagolva)

$\begin{array}{c}{\displaystyle E_{\text{fel}}=2r\pi \ell \alpha =\frac{2V\alpha }{r}\mathrm{,}}\end{array}$

a teljes energia pedig

$\begin{array}{c}{\displaystyle E=E_{\text{cf}}+E_{\text{fel}}=\frac{1}{4}{\omega }^2{r}^2\varrho V+\frac{2V\alpha }{r}\mathrm{.}}\end{array}$

A minimumot deriválással keressük meg: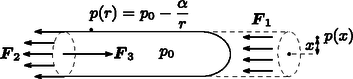

$\begin{array}{c}{\displaystyle \frac{\text{d}E}{\text{d}r}=\frac{1}{2}{\omega }^{2}r\varrho V-\frac{2V\alpha }{r^2}=\mathrm{0,}}\end{array}$

amiből

$\begin{array}{c}{\displaystyle r=\sqrt[3]{\frac{4\alpha }{{\omega }^2\varrho }}\approx 1\mathrm{,}5\text{mm}\text{<span style="font-weight: normal;font-style: normal;">és</span>}\ell =\frac{V}{r^2\pi }\approx 15\text{cm}\mathrm{.}}\end{array}$

Valóban jogos volt tehát az a feltételezés, hogy a buborék alakja közelítőleg egy nyújtott henger.

 

II. megoldás (erőegyensúly). Vágjuk félbe a ,,virslit'', és írjuk fel az erők egyensúlyát (1. ábra)!

 

 

1. ábra

 

A forgó folyadékban a tengelytől $x$ távolságra a nyomás:

$\begin{array}{c}{\displaystyle p\left(x\right)=\frac{1}{2}\varrho {\omega }^2{x}^2+C\mathrm{,}}\end{array}$

ahol $C$ később meghatározandó állandó. A buborékon belül mindenhol ugyanakkora $p_0$ nyomás uralkodik. A henger falánál ez a nyomás a folyadék ottani $p\left(r\right)$ nyomásának és a görbületi nyomásnak az összege:

$\begin{array}{c}{\displaystyle p_0=p\left(r\right)+\frac{\alpha }{r}\mathrm{,}}\end{array}$

amiből

$\begin{array}{c}{\displaystyle p\left(r\right)=p_0-\frac{\alpha }{r}\mathrm{.}}\end{array}$

Ezt összevetve a folyadék nyomáseloszlására felírt összefüggéssel az abban megjelenő $C$ állandó meghatározható:

$\begin{array}{c}{\displaystyle C=p_0-\frac{\alpha }{r}-\frac{1}{2}\varrho {\omega }^2{r}^2\mathrm{.}}\end{array}$

A folyadék által a ,,virsli'' egyik felére kifejtett tengelyirányú erő a folyadék nyomásának egy $r$ sugarú körlapra vett integráljaként számítható ki (2. ábra):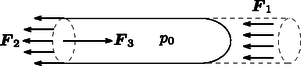

${\displaystyle \begin{array}{cc}\hfill {\displaystyle F_1}& {\displaystyle ={\int }_0^{r}p\left(x\right)\cdot 2\pi x\text{d}x=\frac{1}{2}\varrho {\omega }^2{\int }_0^r{x}^2\cdot 2\pi x\text{d}x+\left(p_0-\frac{\alpha }{r}-\frac{1}{2}\varrho {\omega }^2{r}^2\right)\cdot \pi r^2=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{1}{2}\varrho {\omega }^2\cdot \frac{\pi }{2}{r}^4+p_0\cdot \pi r^2-\alpha \cdot \pi r-\frac{\pi }{2}\varrho {\omega }^2{r}^4=p_0\cdot \pi r^2-\alpha \cdot \pi r-\frac{\pi }{4}\varrho {\omega }^2{r}^4\mathrm{.}}\hfill \end{array}}$

 

 

2. ábra

 

A virsli másik fele által kifejtett húzóerő (a felületi feszültség miatt): $F_2=\alpha \cdot 2\pi r$, míg a másik félben lévő levegő által kifejtett nyomóerő: $F_3=p_0\cdot \pi r^2$.
Az erőegyensúly tehát tengelyirányban így írható fel:

${\displaystyle \begin{array}{cc}\hfill {\displaystyle F_1+F_2}& {\displaystyle =F_3\mathrm{,}}\hfill \\ \hfill {\displaystyle p_0\cdot \pi r^2-\alpha \cdot \pi r-\frac{\pi }{4}\varrho {\omega }^2{r}^4+\alpha \cdot 2\pi r}& {\displaystyle =p_0\cdot \pi r^2\mathrm{,}}\hfill \end{array}}$

amiből az I. megoldással összhangban a következő megoldás adódik:

$\begin{array}{c}{\displaystyle r=\sqrt[3]{\frac{4\alpha }{\varrho {\omega }^2}}\mathrm{.}}\end{array}$

 

2. Egy tartályban $1$ mólnyi egyatomos gáz és $2$ mólnyi kétatomos gáz keveréke található. A tartály fala az egyatomos gáz atomjait átengedi, de a kétatomos gáz molekuláit nem. Kezdetben a tartály a $20{}^{\circ }\text{C}$-os környezettel egyensúlyban van. A tartályban lévő gázkeveréket egy fűtőtest lassan $100{}^{\circ }\text{C}$-kal felmelegíti.
$a)$ Mennyivel változik meg a tartályban lévő gáz belső energiája?
$b)$ Mennyi hőt ad le a fűtőtest a gáznak? (A tartály melegedéséhez szükséges hőt és a tartály hővezetését hagyjuk figyelmen kívül!)
 (Tichy Géza)

 

Megoldás. $a)$ Két gázkeverék akkor van egyensúlyban, ha azon komponensek parciális nyomása megegyezik, melyek a két tartály között áramolhatnak. Feladatunkban csak az egyatomos molekulák gázát engedi át a fal, ezért ha egyensúlyban a tartályban lévő egyatomos gáz parciális nyomása $p_1$, akkor a környezetben ennek a gáznak a parciális nyomása is ugyanakkora. Ez az egyensúly a kétatomos gáz parciális nyomására nem jelent megszorítást.
Először vizsgáljuk az egyatomos gáz folyamatát! Mivel ennek parciális nyomását a környezet állítja be állandóra, ez egy izobár folyamat, de a mólok száma, amely kezdetben $n_{\text{1k}}=1\text{mol}$ nem állandó, hanem a folyamat közben állandóan változik, melegítés hatására gáz áramlik a tartályból a környezetbe. Az egyesített gáztörvény alapján $p_{1}V=n_{1}RT$, ahol $V$ a tartály térfogata. Mivel sem a parciális nyomás, sem a térfogat nem változik, a folyamatra az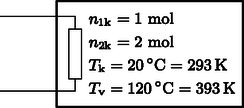

$\begin{array}{c}{\displaystyle n_{1}T=\text{állandó}}\end{array}$

összefüggés jellemző.

 

 

3. ábra

 

A kétatomos gázt a fal nem engedi át, ennélfogva térfogata állandó, a folyamat izochor. A fűtőtest a gázt 20${}^{\circ }$C-ról melegíti 120${}^{\circ }$C-ra, ezért mind az egyatomos gáz, mind a kétatomos gáz kezdeti és végső hőmérséklete kelvinben $T_{\text{k}}=293\text{K}$ és $T_{\text{v}}=393\text{K}$ (3. ábra).
Az egyatomos gáz szabadsági foka 3, ennek ismeretében a belső energia kezdeti értéke:

$\begin{array}{c}{\displaystyle E_{\text{1k}}=\frac{3}{2}{n}_{\text{1k}}R{T}_{\text{k}}\mathrm{,}}\end{array}$

míg belső energiája a folyamat végén:

$\begin{array}{c}{\displaystyle E_{\text{1v}}=\frac{3}{2}{n}_{\text{1v}}R{T}_{\text{v}}=\frac{3}{2}{n}_{\text{1k}}R{T}_{\text{k}}\mathrm{,}}\end{array}$

ami a folyamatra jellemző

$\begin{array}{c}{\displaystyle n_{\text{1v}}{T}_{\text{v}}=n_{\text{1k}}{T}_{\text{k}}}\end{array}$

összefüggés miatt megegyezik a kezdeti energiával. Látjuk, hogy az egyatomos gáz belső energiája nem változik.
A kétatomos gáz öt szabadsági fokkal rendelkezik. A belső energiájának megváltozása:

$\begin{array}{c}{\displaystyle \Delta E_1=\frac{5}{2}{n}_{2}R\left(T_{\text{v}}-T_{\text{k}}\right)\mathrm{.}}\end{array}$

A teljes rendszer belső energiájának megváltozása:

$\begin{array}{c}{\displaystyle \Delta E=\frac{5}{2}{n}_{2}R\left(T_{\text{v}}-T_{\text{k}}\right)=4\mathrm{,}16\text{kJ}\mathrm{.}}\end{array}$

 

$b)$ Most rátérünk annak a hőnek a kiszámítására, amit a fűtőtest ad le. Az egyatomos gáz izobár folyamatában a részecskeszám állandóan változik, tehát az általa felvett hőt részfolyamatonként kell összeadni. Ezt integrállal lehet kifejezni:

$\begin{array}{c}{\displaystyle Q_1=\underset{T_{\text{k}}}{\overset{T_{\text{v}}}{\int }}\frac{5}{2}{n}_{1}R\text{d}T\mathrm{,}}\end{array}$

ahol a folyamat során a mólszám az

$\begin{array}{c}{\displaystyle n_1=\frac{n_{\text{1k}}{T}_{\text{k}}}{T}}\end{array}$

alapján függ a hőmérséklettől. Felhasználtuk, hogy az egyatomos gáz állandó nyomáson vett mólhője $C_{p\text{1}}=\left(5/2\right)R$. Az integrált elvégezve

$\begin{array}{c}{\displaystyle Q_1=\underset{T_{\text{k}}}{\overset{T_{\text{v}}}{\int }}\frac{5}{2}\frac{n_{\text{1k}}R{T}_{\text{k}}}{T}\text{d}T=\frac{5}{2}{n}_{\text{1k}}R{T}_{\text{k}}\text{ln}\frac{T_{\text{v}}}{T_{\text{k}}}=1\mathrm{,}79\text{kJ}\mathrm{.}}\end{array}$

Az integrálás lépése több módon is elkerülhető, például úgy, hogy felhasználjuk a hasonlóságot az izoterm folyamat munkavégzésével, vagy egy közelítő összegzést alkalmazva számolunk numerikusan.
A kétatomos gáz izochor folyamatot végez, ezért az általa felvett hő megegyezik a belső energia megváltozásával:

$\begin{array}{c}{\displaystyle Q_2=\frac{5}{2}{n}_{2}R\left(T_{\text{v}}-T_{\text{k}}\right)=4\mathrm{,}16\text{kJ}\mathrm{.}}\end{array}$

A fűtőtest a kettő hő összegét adja le: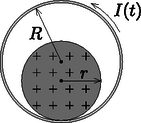

$\begin{array}{c}{\displaystyle Q=Q_1+Q_2=5\mathrm{,}95\text{kJ}\mathrm{.}}\end{array}$

 

3. Egy rögzített, vízszintes tengelyű, légmagos, hosszú szolenoid keresztmetszete $R$ sugarú kör. A tekercs belsejében egy (nem-mágneses) szigetelő anyagból készült, $r$ sugarú tömör henger helyezkedik el. A szigetelő henger pozitívan töltött, egyenletes térfogati eloszlásban. A szolenoidba időben egyenletesen, gyorsan növekvő erősségű áramot vezetünk az ábrán látható körüljárás szerint.

 

 

 

 

Milyen irányban indul el a szigetelő henger? Hogyan függ a válasz az $r/R$ aránytól? Mekkora $r/R$ arány esetén marad a töltött henger nyugalomban?
A tapadási súrlódás elegendően nagy ahhoz, hogy a henger ne csússzon meg. A gördülési ellenállástól tekintsünk el!
 (Vigh Máté)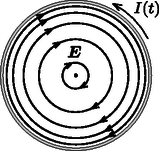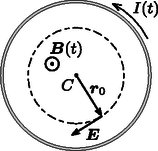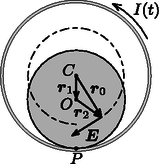

 

Megoldás. A változó (növekvő) erősségű áram hatására a tekercs belsejében időben változó, homogén mágneses mező alakul ki. A változó mágneses mező a Faraday-törvény értelmében időben állandó, forrásmentes és örvényes elektromos mezőt kelt (4. ábra), amely eredő erőt és forgatónyomatékot fejt ki a töltött hengerre: ez mozdíthatja el a hengert egyik vagy másik irányban.

 

 

4. ábra

 

 

 

5. ábra

 

 

 

6. ábra

 

Vizsgáljuk az egész elrendezésnek a szolenoid tengelyére merőleges síkmetszetét! Jelöljük ezen a síkmetszeten a szolenoid középpontját $C$-vel, a szigetelő henger középpontját $O$-val, a henger és a szolenoid érintkezési pontját pedig $P$-vel! A szolenoid belsejében kialakuló indukált elektromos mező térerősségét a Faraday-törvényből határozhatjuk meg, ha azt egy $C$ középpontú, $r_0$ sugarú körre alkalmazzuk (5. ábra):

$\begin{array}{c}{\displaystyle E\left(r_0\right)\cdot 2\pi r_0=\underset{\frac{\Delta \Phi }{\Delta t}}{\overset{}{\underbrace{\pi r_0^2\frac{\Delta B}{\Delta t}}}}\mathrm{,}\text{ahonnan}E\left(r_0\right)=\frac{1}{2}\frac{\Delta B}{\Delta t}{r}_0\mathrm{.}}\end{array}$

Ez az összefüggés a ,,balkéz-szabály'' alapján vektoriálisan is felírható a $C$ pontból a vizsgált pontba mutató ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}}_0$ vektor segítségével:

$\begin{array}{c}{\displaystyle \text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}\left({\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}}_0\right)=-\frac{1}{2}\frac{\Delta B}{\Delta t}{\text{<span style="font-weight: bold;"><span style="font-style: italic;">e</span></span>}}_B\times {\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}}_0\mathrm{,}}\end{array}$

ahol ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">e</span></span>}}_B=\text{<span style="font-weight: bold;"><span style="font-style: italic;">B</span></span>}/|\text{<span style="font-weight: bold;"><span style="font-style: italic;">B</span></span>}|$ a mágneses indukcióvektorral azonos irányú egységvektor.
Vezessük be a 6. ábrán látható ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}}_1$ és ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}}_2$ vektorokat, ahol ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}}_1+{\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}}_2={\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}}_0$. Ezek közül ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}}_1=\overrightarrow{CO}$ konstans vektor (melynek hossza $R-r$), míg ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}}_2$ az $O$ pontból abba a pontba mutat, ahol a térerősségre kíváncsiak vagyunk. Ennek felhasználásával a térerősség így írható: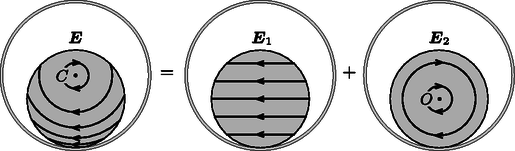

$\begin{array}{c}{\displaystyle \text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}\left({\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}}_0\right)=\underset{{\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_1}{\overset{}{\underbrace{-\frac{1}{2}\frac{\Delta B}{\Delta t}{\text{<span style="font-weight: bold;"><span style="font-style: italic;">e</span></span>}}_B\times {\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}}_1}}}\underset{{\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_2}{\overset{}{\underbrace{-\frac{1}{2}\frac{\Delta B}{\Delta t}{\text{<span style="font-weight: bold;"><span style="font-style: italic;">e</span></span>}}_B\times {\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}}_2}}}\mathrm{,}}\end{array}$

Ebben az összegben az ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_1$-gyel jelölt tag homogén, vízszintesen balra mutató elektromos mezőt, az ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_2$-vel jelölt tag pedig a töltött henger tengelye ($O$ pont) körül ,,örvénylő'' mezőt jelent. Az indukált elektromos teret tehát felbontottuk két mező szuperpozíciójára, ahogy az a 7. ábrán látható.

 

 

7. ábra

 

Azt, hogy a töltött henger jobbra vagy balra indul el az dönti el, hogy a henger legalsó $P$ pontjára vonatkoztatott eredő forgatónyomaték milyen irányba mutat (erre a pontra nézve ugyanis a súrlódási erőnek, a nyomóerőnek és a nehézségi erőnek a forgatónyomatéka is nulla). Az elektromos mező 7. ábrán látható felbontásának az az előnye, hogy segítségével könnyen kiszámítható ez az eredő forgatónyomaték.
A homogén ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_1$ mező $|{\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_1|Q$ nagyságú, a henger $O$ középpontjában ébredő erőt fejt ki a hengerre, melynek forgatónyomatéka a $P$ pontra nézve:

$\begin{array}{c}{\displaystyle M_1=|{\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_1|Qr=\frac{1}{2}\frac{\Delta B}{\Delta t}|{\text{<span style="font-weight: bold;"><span style="font-style: italic;">e</span></span>}}_B\times {\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}}_1|Qr=\frac{1}{2}\frac{\Delta B}{\Delta t}\left(R-r\right)Qr\mathrm{,}}\end{array}$

ahol $Q$ a henger össztöltése, $r$ pedig az erőkar.
Az $O$ pont körül örvénylő ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_2$ mező eredő erőt a szimmetria miatt nem eredményez. A forgatónyomatékhoz viszont ez a mező is ad járulékot, hiszen a henger $O$ pontra nézve átellenes darabkáira ható erők erőpárokat alkotnak. Az erőpárok eredő forgatónyomatéka bármely pontra, így a $P$ és $O$ pontokra számítva is ugyanakkora, de a számolás az $O$ pontra vonatkoztatva egyszerűbb. Az $O$ ponttól $|{\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}}_2|$ távolságra lévő, $\Delta Q$ töltésű kis darabkára $|{\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_2|\Delta Q$ erő hat, így az eredő forgatónyomaték:

$\begin{array}{c}{\displaystyle M_2=\sum |{\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_2|\Delta Q|{\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}}_2|=\frac{1}{2}\frac{\Delta B}{\Delta t}\underset{\frac{1}{2}Q{r}^2}{\overset{}{\underbrace{\sum \Delta Q{|{\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}}_2|}^2}}}\mathrm{.}}\end{array}$

Az összegzésben szereplő kifejezés éppen olyan alakú, mint a henger tehetetlenségi nyomatéka a szimmetriatengelyére vonatkoztatva (csak ott a darabkák $\Delta Q$ töltése helyett azok $\Delta m$ tömege szerepel). Ezt az analógiát felhasználva az összegzés eredménye $Q{r}^2/2$, így

$\begin{array}{c}{\displaystyle M_2=\frac{1}{4}\frac{\Delta B}{\Delta t}Q{r}^2\mathrm{.}}\end{array}$

 

 

8. ábra

 

A $P$ pontra vonatkoztatott $M_1$ forgatónyomaték balra szeretné kitéríteni a töltött hengert, míg az $M_2$ forgatónyomaték jobbra (8. ábra). A henger tehát balra indul el, ha:

$\begin{array}{c}{\displaystyle \underset{M_1}{\overset{}{\underbrace{\frac{1}{2}\frac{\Delta B}{\Delta t}Q\left(R-r\right)r}}}>\underset{M_2}{\overset{}{\underbrace{\frac{1}{4}\frac{\Delta B}{\Delta t}Q{r}^2}}}\mathrm{,}}\end{array}$

azaz ha $r/R<2/\mathrm{3,}$ ellenkező esetben pedig jobbra. Az $r=2R/3$ egyenlőség fennállása esetén a henger egyáltalán nem indul el.

 

Megjegyzés. A hengerre ható, $P$ pontra vonatkoztatott eredő forgatónyomaték irányát a forgómozgással kapcsolatos analógia segítségével is meghatározhatjuk. Vegyük az óramutató járásával ellentétes körüljárási irányokat pozitívnak! Tekintsük a hengert egy $m$ tömegű, homogén tömegeloszlású, a $C$ pont körül $\omega <0$ szögsebességgel forgó merev testnek! Ezen test egy-egy darabkájának sebessége (és emiatt az egységnyi térfogatú kis részének lendülete) éppen olyan irányú és (egy pozitív arányossági tényezőtől eltekintve) ugyanolyan nagyságú, mint az eredeti feladatban az elektromos erőtér által kifejtett erő. Hasonlóan, a forgó merev test kis darabkájának $P$-re vonatkoztatott perdülete (impulzusmomentuma) egy arányossági tényezőtől eltekintve az eredeti feladatban szereplő erők $P$-re vonatkoztatott forgatónyomatékának felel meg. A kérdés tehát az, hogy milyen előjelű a $C$ pont körül negatív irányban forgó henger perdülete a $P$ pontra vonatkoztatva.
Egy merev test teljes perdülete a tömegközéppont körüli forgás ,,sajátperdületéből'' és a tömegközéppontba képzelt, annak sebességével mozgó teljes anyagmennyiség ,,pályaperdületéből'' tehető össze. Esetünkben az $O$ tömegközéppont (balra mutató) sebessége $v_O=\left(R-r\right)\omega$ nagyságú, a pályaperdület tehát $+mr\left(R-r\right)\omega$, a sajátperdület pedig $-\left(1/2\right)m{r}^2\omega$. A $P$ pontra vonatkoztatott teljes perdület tehát:

$\begin{array}{c}{\displaystyle N_P=mr\left(R-r\right)\omega -\frac{1}{2}m{r}^2\omega =\frac{mr\omega }{2}\left(2R-3r\right)\mathrm{.}}\end{array}$

Látható, hogy $r<\frac{2}{3}R$ esetén $N>0$,

 

tehát a henger balra indul el, $r>\frac{2}{3}R$ esetén $N<0$, azaz a henger jobbra indul el, míg $r=\frac{2}{3}R$ esetén nem jön mozgásba.

 

${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{<span style="font-style: italic;">(G. P.) </span>}}\hfill \end{array}}$

 

$*$

 

Az ünnepélyes eredményhirdetésre és díjkiosztásra 2018. november 23-án délután került sor az ELTE TTK Konferenciatermében. Meghívást kaptak az 50 és 25 évvel ezelőtti Eötvös-verseny nyertesei is. Jelen volt az 50 évvel ezelőtti díjazottak közül Vetier András, aki az akkori feladatok ismertetése után röviden beszélt a versenyhez kapcsolódó emlékeiről, és a 25 évvel ezelőtti díjazottak közül Kovács Krisztián.
Ezután következett a 2018. évi verseny feladatainak és megoldásainak bemutatása. Az 1. feladat megoldását Vankó Péter, a 2. feladatét Tichy Géza, a 3. feladatét Vigh Máté ismertette.
Az esemény végén került sor az eredményhirdetésre. A díjakat Sólyom Jenő, az Eötvös Loránd Fizikai Társulat elnöke adta át.
Első díjat a versenybizottság nem adott ki.
Az első feladat hibátlan megoldásáért második díjat nyert Fajszi Bulcsú, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 11. osztályos tanulója, Csefkó Zoltán és Horváth Gábor tanítványa.
A második feladat lényegében helyes megoldásáért harmadik díjat nyert Hajdú Csanád, a BME fizikus hallgatója, a budapesti Eötvös József Gimnázium érettségizett tanulója, Gulyás Erzsébet tanítványa, valamint Vavrik Márton, a BME fizikus hallgatója, a budapesti Berzsenyi Dániel Gimnázium érettségizett tanulója, Lendvai Dorottya és Izsa Éva tanítványa.
Az első feladat helyes közelítő megoldásáért dicséretben részesült Berke Martin, a BME fizikus hallgatója, a Zalaegerszegi Zrínyi Miklós Gimnázium érettségizett tanulója, Bóbics Lilla tanítványa.
A második díjjal Zimányi Gergely adományából 50 ezer, a harmadik díjjal 30 ezer, a dicsérettel 20 ezer forint pénzjutalom járt, a díjazottak tanárai pedig a Typotex Kiadó könyveit kapták. A verseny megszervezését az Eötvös Loránd Fizikai Társulat a MOL támogatásából fedezte.

 

${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{<span style="font-weight: bold;">Tichy Géza, Vankó Péter, Vigh Máté</span>}}\hfill \end{array}}$