Cím:	Megoldásvázlatok a 2019/2. szám emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Ratkó Éva
Füzet:	2019/március, 139 - 147. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Lara $3$ piros, $4$ kék és $3$ sárga építőkockával játszik, melyek legfeljebb csak a színükben különböznek egymástól. Az összes építőkockát egymásra téve szeretne egy tornyot építeni. Hányféle színmintázatú tornyot építhet, ha $a)$ piros kockát sem alulra, sem felülre nem tesz; $b)$ legalább két piros elem közvetlenül egymás fölött van?  (12 pont)   Megoldás. $a)$ Összesen 10 kocka van, tehát 10 emeletes lesz a torony, ebből a 3 piros kockát csak 8 helyre teheti, ami $\left(\genfrac{}{}{0ex}{}{8}{3}\right)=56$ lehetőség. A 4 kék kockát a maradék 7 hely bármelyikére helyezheti, amit $\left(\genfrac{}{}{0ex}{}{7}{4}\right)=35$-féleképpen tehet meg, a sárga kockák helye pedig már egyértelmű. Mivel a piros, illetve kék kockák elhelyezése egymástól függetlenül történik, a színmintázatok száma $56\cdot 35=1960$. $b)$ A két egymás fölötti elemet ragasszuk képzeletben össze, és tekintsük őket egy elemnek (az elemek sorrendjének megszámolása így könnyebb; a színmintázatnál majd figyelembe kell venni, hogy ez 2 kockányi piros szín). A 9 kocka lehetséges sorrendjeinek száma így $2\cdot \frac{9!}{2!4!3!}=2520$, ahol a 2-es szorzó azért van, mert nem mindegy, hogy az 1 szintes és a 2 szintes piros elem hol helyezkedik el. Azonban azt az esetet, ahol mind a három piros kocka egymás fölött van, így kétszer számoltuk. Ragasszuk össze a három piros kockát, így megkapjuk, hogy ezen esetek száma $\frac{8!}{1!4!3!}=280$. Tehát $2520-280=2240$ megfelelő színmintázat van ebben az esetben.   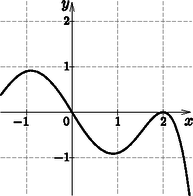2. Az ábra egy $f$ függvény deriváltfüggvényének $\left(f\text{'}\left(x\right)\right)$ egy részletét mutatja. Adjuk meg az alábbi állítások esetén, hogy melyik igaz, melyik hamis, illetve melyiknél nem lehet ezt eldönteni. Válaszunkat indokoljuk. $a)$ A $0$ pontban az $f$ függvénynek lokális maximuma van. $b)$ Ha $0\le x\le 2$, akkor $f\left(x\right)\le 0$. $c)$ Az $f$ függvény képe az origóra szimmetrikus a $\left(-\mathrm{1,1}\right)$ intervallumon.     $d)$ Az $f$ függvénynek az $x=2$ helyen inflexiós pontja van.  (12 pont)   Megoldás. $a)$ Igaz. Az $f\text{'}$ értéke a 0 helyen 0, és pozitívból negatívba vált. $b)$ Nem lehet eldönteni. Az $f\text{'}$ függvény menetéből nem lehet pontosan rekonstruálni az $f$ függvényt. (Egy konstans hozzáadásával $f$ értéke az adott intervallumon pozitívvá vagy negatívvá tehető, míg a deriváltfüggvény nem változik.) $c)$ Hamis. Mivel $f\text{'}$ az origóra középpontosan szimmetrikus (ráadásul egy, az adott intervallumnál valamivel szűkebb intervallumon), így az $f$ függvény az $y$ tengelyre szimmetrikus (ezen a szűkebb intervallumon). $d)$ Igaz. Mivel $f\text{'}\left(2\right)=0$ és nem vált előjelet a 2-ben, így inflexiós pontja van.   3. Krisztiánnak $80$ CD-ből álló gyűjteménye van. A CD-k között $48$ olyan van, amin több előadó szerepel (T), $24$ olyan van, amin egy előadó vagy együttes számai vannak (E), és $8$ hangszeres zenei CD-je (H) is van. Sajnos Krisztián nem túl rendes, és az összes CD egy fiókban hever egymás hegyén-hátán. Egyik barátja megkéri, hogy vigyen el a partijára $5$ CD-t. Mivel ‐ mint mindig ‐ Krisztián nagy rohanásban van, anélkül, hogy a fiókba nézne, kivesz onnan $5$ CD-t. $a)$ Mi a valószínűsége annak, hogy csak hangszerest visz? $b)$ Mi a valószínűsége, hogy az öt CD között lesz legalább egy (T), viszont nem lesz (H)? $c)$ Krisztián rápillantott a kezében lévő CD-kre, és látta, hogy a legfelső (H). Mi a valószínűsége, hogy a többi is az?  (13 pont)   Megoldás. $a)$ A jó esetek száma $\left(\genfrac{}{}{0ex}{}{8}{5}\right)=56$, az összes eset száma $\left(\genfrac{}{}{0ex}{}{80}{5}\right)=24040\mathrm{016,}$ így a valószínűség $p_a=\frac{56}{24040016}\left(\approx 2\mathrm{,}33\cdot {10}^{-6}\right)$. $b)$ 1, 2, 3, 4 vagy 5 (T), és ennek megfelelően 4, 3, 2, 1 vagy 0 (E) lesz a választott lemezek között (és nyilván mindig 0 (H), amit $\left(\genfrac{}{}{0ex}{}{8}{0}\right)=0=1$-féleképp választhatunk ki, de ezt nem szükséges leírni): $\begin{array}{c}{\displaystyle p_b=\frac{\left(\genfrac{}{}{0ex}{}{48}{1}\right)\left(\genfrac{}{}{0ex}{}{24}{4}\right)+\left(\genfrac{}{}{0ex}{}{48}{2}\right)\left(\genfrac{}{}{0ex}{}{24}{3}\right)+\left(\genfrac{}{}{0ex}{}{48}{3}\right)\left(\genfrac{}{}{0ex}{}{24}{2}\right)+\left(\genfrac{}{}{0ex}{}{48}{4}\right)\left(\genfrac{}{}{0ex}{}{24}{1}\right)+\left(\genfrac{}{}{0ex}{}{48}{5}\right)\left(\genfrac{}{}{0ex}{}{24}{0}\right)}{\left(\genfrac{}{}{0ex}{}{80}{5}\right)}\approx 0\mathrm{,}58.}\end{array}$ $c)$ Használjuk a feltételes valószínűségre vonatkozó képletet (itt most számít a sorrend): $\begin{array}{c}{\displaystyle p_c=\frac{P\left(\text{<span style="font-weight: normal;font-style: normal;">első az és a többi is az</span>}\right)}{P\left(\text{<span style="font-weight: normal;font-style: normal;">első az</span>}\right)}=\frac{\frac{8\cdot 7\cdot 6\cdot 5\cdot 4}{80\cdot 79\cdot 78\cdot 77\cdot 76}}{\frac{8\cdot 79\cdot 78\cdot 77\cdot 76}{80\cdot 79\cdot 78\cdot 77\cdot 76}}=\frac{7\cdot 6\cdot 5\cdot 4}{79\cdot 78\cdot 77\cdot 76}\left(\approx 2\mathrm{,}33\cdot {10}^{-5}\right)\mathrm{.}}\end{array}$   4. Oldjuk meg a következő egyenleteket a valós számok halmazán: $a)$ $2^{4x-1}\cdot 4^{2x+3}=8^x$; $b)$ $\sqrt[]{x-\sqrt[]{x+2}}\le 2$.  (14 pont)   Megoldás. $a)$ Alakítsuk át mindkét oldalt: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2^{4x-1}\cdot 2^{4x+6}}& {\displaystyle =2^{3x}\mathrm{,}}\hfill \\ \hfill {\displaystyle 2^{8x+5}}& {\displaystyle =2^{3x}\mathrm{.}}\hfill \end{array}}$ Az exponenciális függvény szigorú monotonitása miatt ebből $8x+5=3x$, és így $x=-1$ következik, ami az ekvivalens lépések miatt megoldása az egyenletnek. $b)$ A bal oldal nemnegatív, így az egyenlőtlenséget négyzetre emelhetjük: $x-\sqrt[]{x+2}\le 4$, de $0\le x-\sqrt[]{x+2}$-nek is teljesülnie kell. Ekkor $x\ge \sqrt[]{x+2}\ge 0$, amiből $x^2\ge x+2$, vagyis $x^2-x-2=\left(x+1\right)\left(x-2\right)\ge 0$. Ebből pedig $x\ge 2$ vagy $x\le -1$ következik, de ez utóbbi ellentmond az $x\ge 0$ feltételnek. A belső gyökjel alatt is nemnegatív szám kell, hogy álljon, vagyis $x\ge -2$. A kettőt összevetve $x\ge 2$ adódik. Ekkor megoldandó az $x-4\le \sqrt[]{x+2}$ egyenlőtlenség. Ha $2\le x<4$, akkor a bal oldal negatív, a jobb oldal pozitív, tehát ez megfelelő. Ha $x\ge 4$, akkor négyzetre emelve az $x^2-8x+16\le x+2$ egyenlőtlenséget kapjuk, amiből $x^2-9x+14=\left(x-2\right)\left(x-7\right)\le 0$, azaz $2\le x\le 7$. Ekkor tehát $4\le x\le 7$. Az egyenlőtlenség megoldása: $2\le x\le 7$.   II. rész     5. A Schiller Gimnázium diákjainak mindegyike első idegen nyelvként angolt tanul, és legalább egy, legfeljebb két nyelvet választhatnak a francia, spanyol és latin közül. A $10$. évfolyam $72$ diákjából $40$-en két nyelvet is választottak. $48$-an tanulnak franciául, $40$-en spanyolul és valahányan latinul. $24$-en tanulnak franciául és spanyolul is, és $12$-en franciául és latinul. $a)$ Hányan tanulnak összesen latinul; és ebből hányan spanyolul is? Az évfolyamról egy tanulót véletlenszerűen kiválasztva mi annak a valószínűsége, hogy $b)$ franciául és spanyolul, $c)$ franciául vagy spanyolul, $d)$ vagy franciául, vagy latinul (de nem mindkét nyelven) tanul?  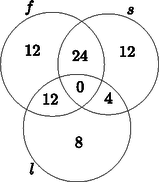(16 pont)   Megoldás. Kezdjük el kitölteni a Venn-diagramot. Jelöljük a nyelveket kezdőbetűjükkel. A 40 diák közül, akik 2 plusz nyelvet is választottak, 24-en franciául és spanyolul, 12-en francia és latin nyelven, tehát $40-24-12=4$ tanuló választotta a spanyolt és latint. A 40 spanyolul tanuló közül $24+4=28$ tanuló választott még egy nyelvet, így $40-28=12$ diák tanul csak spanyolul (az angol mellett, amire ezután nem térünk ki). A csak franciául tanuló diákok száma $48-24-12=12$. Végül, a csak latinul tanulók száma $72-\left(24+12+4+12+12\right)=8$.     $a)$ Tehát összesen $12+4+8=24$ diák tanul latint, és ebből 4 spanyolt is. $b)$ $p_{fs}=\frac{24}{72}=\frac{1}{3}$. $c)$ $p_{f\vee s}=\frac{48+16}{72}=\frac{64}{72}=\frac{8}{9}$. $d)$ $p_{f\overline{l}\vee \overline{f}l}=\frac{\left(12+24\right)+\left(8+4\right)}{72}=\frac{48}{72}=\frac{2}{3}$.   6. Egy parkban néhány, betonból készült, félgömb formájú virágtartót használnak. A félgömbök belső sugara 44 cm, falvastagsága 8 cm, a beton sűrűsége 2,2 g/${\text{cm}}^3$. $a)$ Hány ${\text{m}}^3$ virágföld fér egy ilyen tartóba? $b)$ Milyen nehéz egy tartó? 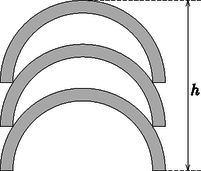$c)$ A tél beállta előtt mindegyik tartót kiürítik, majd hármat-hármat egymásra helyeznek. Milyen magas egy ilyen rakás?     $d)$ Tavasszal újra kihelyezik a tartókat. Előtte fehérre meszelik a tartók külső részét (a peremet is). Egy-egy virágtartónak mekkora területű része lesz így frissen meszelve (${\text{cm}}^2$-ben)?  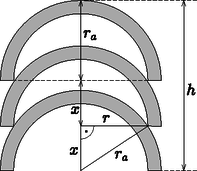(16 pont)   Megoldás. Használjuk az ábra jelöléseit. A virágtartók belső sugara $r=44$ cm, külső sugara $r_a=52$ cm, két egymásra rakott tartó aljának távolsága pedig $x$. $a)$ A tartóba tehető virágföld térfogata: $\begin{array}{c}{\displaystyle V_{\text{<span style="font-weight: normal;font-style: normal;">virágföld</span>}}=\frac{1}{2}\cdot \frac{4}{3}\pi r^3\approx 0\mathrm{,}178{\text{<span style="font-weight: normal;font-style: normal;">m</span>}}^3\mathrm{.}}\end{array}$     $b)$ A tartó térfogata: $\begin{array}{c}{\displaystyle V_{\text{<span style="font-weight: normal;font-style: normal;">tartó</span>}}=\frac{1}{2}\cdot \frac{4}{3}\pi \left(r_a^3-r^3\right)\approx 116080{\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^3\mathrm{.}}\end{array}$ A tartó tömege: $m=\varrho \cdot V\approx 255\text{<span style="font-weight: normal;font-style: normal;">kg</span>}$. $c)$ A Pitagorasz-tételt felírva: $r_a^2=x^2+r^2$, amiből $x\approx 27\mathrm{,}7\text{<span style="font-weight: normal;font-style: normal;">cm</span>}$, és így a kérdezett magasság: $h=2x+r_a\approx 107\mathrm{,}4\text{<span style="font-weight: normal;font-style: normal;">cm</span>}$. 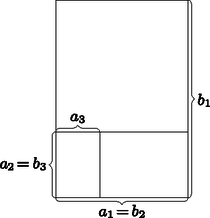$d)$ A lefestendő felület áll egy $r_a$ sugarú félgömbből, valamint egy $r_a$ és $r$ sugarú kör által meghatározott körgyűrűből: $\begin{array}{c}{\displaystyle F=\frac{1}{2}\cdot 4\pi r_a^2+\pi \left(r_a^2-r^2\right)=\pi \left(3r_a^2-r^2\right)\approx 19402\mathrm{,}48{\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^2\mathrm{.}}\end{array}$   7. Egy téglalap oldalai $a_1=2$ m és $b_1=3$ m. Felosztjuk két téglalapra az ábrán látható módon úgy, hogy az egyik hasonló az elsőhöz, oldalai $a_2$ és $b_2=a_1$. Ezt a második téglalapot is felosztjuk úgy, hogy a kapott két téglalap közül az egyik hasonló hozzá, és ennek a harmadik téglalapnak az oldalai $a_3$ és $b_3=a_2$. Ezt az eljárást folytatjuk. $a)$ Milyen hosszúak az $n$-edik téglalap oldalai? $b)$ Milyen $n$ esetén lesz az $n$-edik és az $\left(n+1\right)$-edik téglalap területének különbsége 1 ${\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^2$-nél kisebb?     $c)$ Mekkora az első $n$ téglalap kerületének összege?  (16 pont)   Megoldás. $a)$ $b_1=3$ m, $a_1=2$ m =$\frac{2}{3}{b}_1$; $b_2=a_1=\frac{2}{3}{b}_1$; $a_2=\frac{2}{3}{b}_2=(\frac{2}{3}{)}^2\cdot b_1$; $b_n=a_{n-1}=\frac{2}{3}{b}_{n-1}=(\frac{2}{3}{)}^{n-1}\cdot b_1$; $a_n=\frac{2}{3}{b}_n=(\frac{2}{3}{)}^n\cdot b_1$. $b)$ Írjuk fel az $n$. és az $\left(n+1\right)$. téglalap területét: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_n}& {\displaystyle =a_n\cdot b_n={\left(\frac{2}{3}\right)}^n\cdot b_1\cdot {\left(\frac{2}{3}\right)}^{n-1}\cdot b_1={\left(\frac{2}{3}\right)}^{2n-1}\cdot b_1^2\mathrm{,}}\hfill \\ \hfill {\displaystyle T_{n+1}}& {\displaystyle =a_{n+1}\cdot b_{n+1}={\left(\frac{2}{3}\right)}^{n+1}\cdot b_1\cdot {\left(\frac{2}{3}\right)}^n\cdot b_1={\left(\frac{2}{3}\right)}^{2n+1}\cdot b_1^2\mathrm{.}}\hfill \end{array}}$ A kettő különbsége: $\begin{array}{c}{\displaystyle T_n-T_{n+1}={\left(\frac{2}{3}\right)}^{2n-1}\cdot \left(1-{\left(\frac{2}{3}\right)}^2\right)\cdot b_1^2\mathrm{.}}\end{array}$ Mivel $b_1=300$ cm, azért ez pontosan akkor kisebb 1 cm${}^2$-nél, ha $\begin{array}{c}{\displaystyle {\left(\frac{2}{3}\right)}^{2n-1}\cdot \left(1-{\left(\frac{2}{3}\right)}^2\right)<\frac{1}{90000}\mathrm{.}}\end{array}$ Ekvivalens átalakításokat végezve ebből: ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left({\displaystyle \frac{2}{3}}\right)}^{2n-1}}& {\displaystyle <{\displaystyle \frac{1}{50000}}\mathrm{,}}\hfill \\ \hfill {\displaystyle \left(2n-1\right)\cdot \text{lg}{\displaystyle \frac{2}{3}}}& {\displaystyle <\text{lg}{\displaystyle \frac{1}{50000}}\mathrm{,}}\hfill \end{array}}}\hfill \\ \hfill {\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle 2n-1}& {\displaystyle >{\displaystyle \frac{\text{lg}\frac{1}{50000}}{\text{lg}\frac{2}{3}}}={\displaystyle \frac{-\text{lg}50000}{\text{lg}2-\text{lg}3}}\mathrm{,}}\hfill \\ \hfill {\displaystyle n}& {\displaystyle >{\displaystyle \frac{1}{2}}-{\displaystyle \frac{\text{lg}50000}{2\left(\text{lg}2-\text{lg}3\right)}}\approx 13\mathrm{,}8.}\hfill \end{array}}}\hfill \end{array}}$ Tehát $n\ge 14$ esetén lesz az $n$-edik és az ($n+1$)-edik téglalap területének különbsége 1 cm${}^2$-nél kisebb. $c)$ Az első $n$ téglalap kerületének összege: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle }& {\displaystyle }\hfill & {\displaystyle 2\cdot (\left({\left(\frac{2}{3}\right)}^1\cdot 3+{\left(\frac{2}{3}\right)}^2\cdot 3+{\left(\frac{2}{3}\right)}^3\cdot 3+\text{...}+{\left(\frac{2}{3}\right)}^n\cdot 3\right)+}\hfill \\ \hfill {\displaystyle }& {\displaystyle }\hfill & {\displaystyle +\left(3+\frac{2}{3}\cdot 3+{\left(\frac{2}{3}\right)}^2\cdot 3+{\left(\frac{2}{3}\right)}^3\cdot 3+\text{...}+{\left(\frac{2}{3}\right)}^{n-1}\cdot 3\right))=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =}\hfill & {\displaystyle 2\cdot \left(3\cdot 2\cdot \left(1+\frac{2}{3}+{\left(\frac{2}{3}\right)}^2+{\left(\frac{2}{3}\right)}^3+\text{...}+{\left(\frac{2}{3}\right)}^{n-1}\right)+3\cdot {\left(\frac{2}{3}\right)}^n-3\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =}\hfill & {\displaystyle 12\cdot \left(\frac{1-(\frac{2}{3}{)}^n}{1-\frac{2}{3}}\right)+6\cdot {\left(\frac{2}{3}\right)}^n-6=30-30\cdot {\left(\frac{2}{3}\right)}^n\mathrm{.}}\hfill \end{array}}$   8. Egy kalandpark pályáján két fa között egy függőhíd található. A felfüggeszett híd alakjának általános képlete $f\left(x\right)=a\cdot \frac{e^{kx}+e^{-kx}}{2k}$, ahol $a$ és $k$ valós paraméterek. Az 1. ábrán az $a=1$ és $k=0\mathrm{,}5$, $k=1$, illetve $k=2$ értékekhez tartozó láncgörbék láthatók.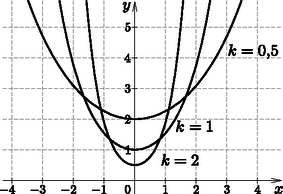1   1. ábra  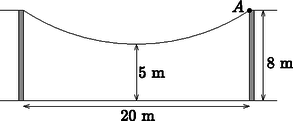 2. ábra $a)$ A 2. ábrán a híd vázlatos oldalnézetét látjuk. Határozzuk meg a híd görbéjéhez tartozó két paraméter értékét $3$ tizedesjegyre kerekítve (a talajszintet tekintsük az $x$-tengelynek.) $b)$ Határozzuk meg, hogy az $A$ pontban a híd milyen szöget zár be a vízszintessel. $c)$ Reklámfelülelet szeretnének felszerelni a híd egyik oldalára úgy, hogy a felülelet a talajszint, a híd és a két fa zárja közre. Mekkora felület keletkezik így?   (16 pont)   Megoldás. $a)$ $f\left(0\right)=5$, vagyis $5=a\cdot \frac{e^0+e^0}{2k}$, amiből $5k=a$. Tudjuk még, hogy $\begin{array}{c}{\displaystyle 8=f\left(10\right)=a\cdot \frac{e^{10k}+e^{-10k}}{2k}=5k\cdot \frac{e^{10k}+e^{-10k}}{2k}\mathrm{,}}\end{array}$ amiből $3\mathrm{,}2=e^{10k}+e^{-10k}$. Legyen $u=e^{10k}$, ekkor $u$-val beszorozva kapjuk, hogy $u^2-3\mathrm{,}2u+1=0$, amiből $u_{\mathrm{1,2}}=\frac{3\mathrm{,}2\pm \sqrt[]{10\mathrm{,}24-4}}{2}\approx \frac{3\mathrm{,}2\pm 2\mathrm{,}5}{2}$, azaz $u_1=2\mathrm{,}85$ és $u_2=0\mathrm{,}35$ (a két szám egymás reciproka). Ebből $k_1=0\mathrm{,}105$, $k_2=-0\mathrm{,}105$ és a megfelelő $a$ értékek $a_1=0\mathrm{,}525$ és $a_2=-0\mathrm{,}525$. (A láncgörbéknél a pozitív értékeket szokás használni.) $b)$ $f\left(x\right)=2\mathrm{,}5\left(e^{0\mathrm{,}105x}+e^{-0\mathrm{,}105x}\right)$, amiből $f\text{'}\left(x\right)=2\mathrm{,}5\cdot 0\mathrm{,}105\left(e^{0\mathrm{,}105x}-e^{-0\mathrm{,}105x}\right)$, és így $f\text{'}\left(10\right)\approx 0\mathrm{,}658$. A keresett szöget $\alpha$-val jelölve $\text{tg}\alpha =f\text{'}\left(10\right)=0\mathrm{,}658$, amiből $\alpha \approx 33\mathrm{,}{3}^{\circ }$. Tehát az $A$ pontban a híd körülbelül ${33}^{\circ }$-os szöget zár be a vízszintessel. $c)$ ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T}& {\displaystyle =2\cdot \underset{0}{\overset{10}{\int }}2\mathrm{,}5\left(e^{0\mathrm{,}105x}+e^{-0\mathrm{,}105x}\right)\text{d}x=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =2\cdot {\left[2\mathrm{,}5\left(\frac{1}{0\mathrm{,}105}{e}^{0\mathrm{,}105x}-\frac{1}{0\mathrm{,}105}{e}^{-0\mathrm{,}105x}\right)\right]}_0^{10}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =5\left(\frac{1}{0\mathrm{,}105}{e}^{\mathrm{1,05}}-\frac{1}{0\mathrm{,}105}{e}^{-\mathrm{1,05}}\right)-5\left(\frac{1}{0\mathrm{,}105}{e}^0-\frac{1}{0\mathrm{,}105}{e}^0\right)\approx 119\mathrm{,}41{\text{<span style="font-weight: normal;font-style: normal;">m</span>}}^2\mathrm{.}}\hfill \end{array}}$   9. $a)$ Hány osztója van a $2018\cdot 2019$, illetve a ${2018}^{2019}$ számnak? $b)$ Mennyi az egyik, illetve a másik szám osztóinak az összege? $c)$ Bizonyítsuk be, hogy ${2018}^{2019}$ legalább $3\cdot 2019$ számjegyből áll. $d)$ Melyik nagyobb: ${2018}^{2019}$ vagy ${2019}^{2018}?$  (16 pont)   Megoldás. $a)$ $2018=2\cdot 1009$, $2019=3\cdot 673$, így az osztók száma: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle d\left(2018\cdot 2019\right)}& {\displaystyle =d\left(2\cdot 3\cdot 673\cdot 1009\right)=2^4=\mathrm{16,}}\hfill \\ \hfill {\displaystyle d\left({2018}^{2019}\right)}& {\displaystyle =d\left(2^{2019}\cdot {1009}^{2019}\right)={2020}^2=4080400.}\hfill \end{array}}$ $b)$ $2018\cdot 2019$ osztói: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \mathrm{1,}\mathrm{2,}\mathrm{1009,}2018;3\cdot 1=3;3\cdot 2=6;3\cdot 1009=3027;3\cdot 2018=6054;}\hfill \\ \hfill {\displaystyle 673\cdot 1=673;673\cdot 2=1346;673\cdot 1009=679057;673\cdot 2018=1358114;}\hfill \\ \hfill {\displaystyle 2019\cdot 1=2019;2019\cdot 2=4038;2019\cdot 1009=2037171;2019\cdot 2018=4074342.}\hfill \end{array}}$ Összegük $8168880$. (Ezt az összeget így is kiszámolhatjuk: $\begin{array}{c}{\displaystyle \frac{2^2-1}{2-1}\cdot \frac{{1009}^2-1}{1009-1}\cdot \frac{3^2-1}{3-1}\cdot \frac{{673}^2-1}{673-1}=3\cdot 1010\cdot 4\cdot 674=8168880.)}\end{array}$ ${2018}^{2019}$ osztóit az első módszerrel nehéz lenne összeszámolni. Vegyük észre, hogy minden osztó $2^k\cdot {1009}^l$ alakú, ahol $k$ és $l$ 0 és 2019 közötti tetszőleges egész szám lehet. Tehát az osztók összegét felírhatjuk $\begin{array}{c}{\displaystyle \sum _{k=0}^{2019}{2}^k\cdot \sum _{l=0}^{2019}{1009}^l}\end{array}$ alakban, hiszen minden osztó két szám szorzata az alábbi táblázatban:     Az összes lehetséges szorzat összege így $\begin{array}{c}{\displaystyle \frac{{1009}^{2020}-1}{1009-1}\cdot \frac{2^{2020}-1}{2-1}=\frac{{1009}^{2020}-1}{1008}\cdot \left(2^{2020}-1\right)\mathrm{.}}\end{array}$ c) ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle {2018}^{2019}}& {\displaystyle >{\left(2\cdot {10}^3\right)}^{2019}=2^{2019}\cdot {10}^{3\cdot 2019}={\left(2^{10}\right)}^{201}\cdot 2^9\cdot {10}^{6057}>}\hfill & \text{(<mi>*</mi>)}\\ \hfill {\displaystyle }& {\displaystyle >{\left({10}^3\right)}^{201}\cdot 2^9\cdot {10}^{6057}={10}^{603}\cdot 2^9\cdot {10}^{6057}=512\cdot {10}^{6660}>}\hfill \\ \hfill {\displaystyle }& {\displaystyle >5\cdot {10}^2\cdot {10}^{6660}=5\cdot {10}^{6662}\mathrm{,}}\hfill \end{array}}$ ami legalább $6663>6057=3\cdot 2019$ számjegy. d) ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle {2018}^{2019}}& {\displaystyle ?{2019}^{2018}\mathrm{,}}\hfill & \text{(<mi>*</mi>)}\\ \hfill {\displaystyle 2018}& {\displaystyle ?{\left(\frac{2019}{2018}\right)}^{2018}=2\mathrm{,}7176\text{...}\mathrm{.}}\hfill \end{array}}$ Tehát ${2018}^{2019}$ a nagyobb. 1A 8. feladat szövegéből eredetileg kimaradt, hogy a görbék az $a=1$ értékhez tartoznak.