Bemutatjuk Euler arányösszeg-tételének történetét, adunk rá egy új bizonyítást, és egy érdekes egyenlőtlenséggé alakítjuk Euler arányösszeg-formuláját.¹

 

 

 

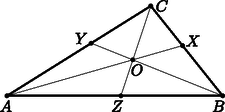Habár Euler már 1780. május 1-jén benyújtotta a kiadónak az arányösszeg-tételt tartalmazó tanulmányát [2], az csak 1783-ban bekövetkezett halála után 22 évvel jelent meg. Sok munkája jutott erre a sorsa, aminek legfőbb oka az volt, hogy valósággal ontotta magából a cikkeket (élete során több, mint 800-at írt a 28 nagyobb mű mellett), így az általa preferált Berlini, illetve Szentpétervári Akadémiák folyóiratainál kiadatlan művei igencsak feltorlódtak.
A kortársak azonban ismerték Euler arányösszeg-tételét, amit jól mutat, hogy Anders Johan Lexell (1740‐1783), aki az Euler-család jó barátja volt, és haláláig ugyanannak a Szentpétervári Akadémiának volt a tagja, már 1784-ben publikálta a tétel gömbháromszögekre érvényes változatát [3].
Jelen szerzőknek is egy általánosabb problémával, a projektív-metrikus terek karakterizációjával [8] összefüggésben került látóterébe az arányösszeg-tétel [7].
Még az arányösszeg-tételnél is kevésbé ismert, pedig már Euler [2] dolgozatában is szerepelt, hogy az $ABC$ háromszög megszerkeszthető az (1) formulában szereplő hosszak ismeretében.

 

2. tétel (Szerkeszthetőség). Ha adottak egy ismeretlen $ABC$ háromszög valamely $O$ pontjára illeszkedő $AX$, $BY$ és $CZ$ szakaszok hosszai, valamint azok $O$ pont általi felosztásának arányai, akkor az $ABC$ háromszög megszerkeszthető.

 

Ebben a dolgozatban nemcsak a fenti tételeket igazoljuk, hanem a 3. tételben pontosan megadjuk annak feltételeit is, hogy három olyan szakaszt, amelyek belsejében adott egy-egy pont, mikor lehet ezen belső pontjaikban úgy összeilleszteni, hogy a valamely három kiválasztott végpontjuk által meghatározott háromszögnek a kiválasztott végponttal szemben lévő oldalai tartalmazzák a szakaszok nem kiválasztott végpontjait².
Végül, bár bemutatjuk a közvetlen általánosítás lehetőségét is, inkább egy az (1) egyenlőségből született egyenlőtlenséget bizonyítunk, mely éppenséggel pontosan akkor válik egyenlőséggé, ha az $AX$, $BY$ és $CZ$ szakaszok egy ponton mennek át. A 4. tétel határozottan emlékeztet Routh tételére ([1, 13.55], [11]).

 

2. Az arányösszeg-tétel és megfordításának bizonyítása

 

Az 1. tétel bizonyítása. Áttekinthetőbbé válik Euler (1) formulája, ha bevezetjük az $a=\frac{AO}{OX}$, $b=\frac{BO}{OY}$ és $c=\frac{CO}{OZ}$ jelöléseket:

$\begin{array}{c}{\displaystyle a+b+c+2=abc\mathrm{.}}\end{array}$

(2)

Mindkét oldalhoz hozzáadva az $1+a+b+c+ab+bc+ca$ kifejezést, a jobb oldal újra szorzatalakba írható, és a bal oldal is szorzatok összegévé válik:

$\begin{array}{c}{\displaystyle \left(1+b\right)\left(1+c\right)+\left(1+a\right)\left(1+c\right)+\left(1+a\right)\left(1+b\right)=\left(1+a\right)\left(1+b\right)\left(1+c\right)\mathrm{.}}\end{array}$

Az $a$, $b$ és $c$ értéke nyilván nem $-1$, ezért a jobb oldallal osztva az ekvivalens

$\begin{array}{c}{\displaystyle \frac{1}{1+a}+\frac{1}{1+b}+\frac{1}{1+c}=1}\end{array}$

(3)

egyenlőséghez jutunk, vagyis (1) ekvivalens az

$\begin{array}{c}{\displaystyle \frac{OX}{AX}+\frac{OY}{BY}+\frac{OZ}{CZ}=1}\end{array}$

(4)

egyenlőséggel. Ez azonban közvetlenül adódik az

$\begin{array}{c}{\displaystyle \frac{OX}{AX}=\frac{t\left(OBC\right)}{t\left(ABC\right)}\mathrm{,}\frac{OY}{BY}=\frac{t\left(OCA\right)}{t\left(ABC\right)}\mathrm{,}\frac{OZ}{CZ}=\frac{t\left(OAB\right)}{t\left(ABC\right)}}\end{array}$

egyenlőségekből.  $\square$

 

A 2. tétel bizonyítása. Annak érdekében, hogy elkerüljük az áttekinthetetlenül összetett formulákat, most is alkalmazzuk az $a=\frac{AO}{OX}$, $b=\frac{BO}{OY}$ és $c=\frac{CO}{OZ}$ jelöléseket, melyekre a feltétel szerint (2), vagy ami ugyanaz, (3) teljesül. Bevezetjük még az $\alpha =ZOB\sphericalangle$, $\beta =XOC\sphericalangle$ és $\gamma =YOA\sphericalangle$ szögeket, amelyekre nyilván $\alpha +\beta +\gamma =\pi$ érvényes.

 

 

Feladatunk tehát az $\alpha$, $\beta$ és $\gamma =\pi -\alpha -\beta$ értékek megtalálása.
Az $X$ pont akkor és csak akkor esik a $BC$ szakaszra, ha

$\begin{array}{c}{\displaystyle BO\cdot OC\text{sin}\alpha =t\left(BOC\right)=BO\cdot OX\text{sin}\gamma +CO\cdot OX\text{sin}\beta \mathrm{,}}\end{array}$

vagyis

$\begin{array}{c}{\displaystyle \frac{AO}{OX}\cdot \frac{\text{sin}\alpha }{OA}=\frac{\text{sin}\alpha }{OX}=\frac{\text{sin}\gamma }{OC}+\frac{\text{sin}\beta }{BO}\mathrm{.}}\end{array}$

A csúcsok ciklikus permutációjával ugyanígy látjuk, hogy $Y\in CA$ és $Z\in AB$ akkor és csak akkor igaz, ha rendre

${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{BO}{OY}\cdot \frac{\text{sin}\beta }{OB}}& {\displaystyle =\frac{\text{sin}\alpha }{OA}+\frac{\text{sin}\gamma }{CO}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{CO}{OZ}\cdot \frac{\text{sin}\gamma }{OC}}& {\displaystyle =\frac{\text{sin}\beta }{OB}+\frac{\text{sin}\alpha }{AO}\mathrm{.}}\hfill \end{array}}$

Az $x=\frac{\text{sin}\alpha }{AO}$, $y=\frac{\text{sin}\beta }{OB}$ és $z=\frac{\text{sin}\gamma }{OC}$ bevezetésével azt kapjuk, hogy ezek teljesítik az

${\displaystyle \begin{array}{ccc}\hfill {\displaystyle ax-y-z}& {\displaystyle =\mathrm{0,}}\hfill & \text{(<mn>5</mn>)}\\ \hfill {\displaystyle -x+by-z}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle -x-y+cz}& {\displaystyle =0}\hfill \end{array}}$

homogén lineáris egyenletrendszert. Az (5) egyenleteinek különbségéből rögtön adódik, hogy a megoldásokra $\left(1+a\right)x=\left(1+b\right)y=\left(1+z\right)c$ teljesül, vagyis minden megoldás $(\frac{\lambda }{1+a}\mathrm{,}\frac{\lambda }{1+b}\mathrm{,}\frac{\lambda }{1+c})$ alakú, ahol $\lambda \in \text{R}$. Eszerint

$\begin{array}{c}{\displaystyle \lambda \frac{AO}{1+a}=\text{sin}\alpha \mathrm{,}\lambda \frac{BO}{1+b}=\text{sin}\beta \text{és}\lambda \frac{CO}{1+c}=\text{sin}\gamma \mathrm{.}}\end{array}$

(6)

Ebből

$\begin{array}{c}{\displaystyle \frac{OB}{1+b}\text{sin}\alpha =\frac{OA}{1+a}\text{sin}\beta \mathrm{,}}\end{array}$

és

${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{OC}{1+c}}& {\displaystyle =\frac{\text{sin}\gamma }{\lambda }=\frac{\text{sin}\alpha \text{cos}\beta +\text{sin}\beta \text{cos}\alpha }{\lambda }=\frac{\text{sin}\alpha }{\lambda }\text{cos}\beta +\text{cos}\alpha \frac{\text{sin}\beta }{\lambda }=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{OA}{1+a}\text{cos}\beta +\frac{OB}{1+b}\text{cos}\alpha }\hfill \end{array}}$

is következik. Utóbbi egyenlőség mindkét oldalából kivonva az $\frac{OB}{1+b}\text{cos}\alpha$ kifejezést, majd az eredményt négyzetre emelve és hozzáadva az első egyenlethez, azt kapjuk, hogy

$\begin{array}{c}{\displaystyle \frac{O{B}^2}{{\left(1+b\right)}^2}\text{sin}{}^2\alpha +{\left(\frac{OC}{1+c}-\frac{OB}{1+b}\text{cos}\alpha \right)}^2=\frac{O{A}^2}{{\left(1+a\right)}^2}\mathrm{.}}\end{array}$

Ebből a bal oldalon a különbség négyzetre emelését elvégezve

$\begin{array}{c}{\displaystyle \frac{O{B}^2}{{\left(1+b\right)}^2}-2\cdot \frac{OC}{1+c}\cdot \frac{OB}{1+b}\text{cos}\alpha +\frac{O{C}^2}{{\left(1+c\right)}^2}=\frac{O{A}^2}{{\left(1+a\right)}^2}}\end{array}$

(7)

adódik. Ez a koszinusz-tétel értelmében azt jelenti, hogy van egy olyan $PQR$ háromszög, amelynek a csúcsokkal szembeni oldalhosszaira rendre $p=\frac{OA}{1+a}$, $q=\frac{OB}{1+b}$ és $r=\frac{OC}{1+c}$ érvényes, és szögei a csúcsoknál rendre $\alpha$, $\beta$ és $\gamma =\pi -\alpha -\beta$.
Az eredeti háromszöget tehát úgy tudjuk megszerkeszteni, hogy a $p=\frac{AO\cdot OX}{AX}$, $q=\frac{BO\cdot OY}{BY}$ és $r=\frac{CO\cdot OZ}{CZ}$ hosszakat kiszámítjuk, ezekből megszerkesztjük a $PQR$ háromszöget, ennek szögei megadják az $\alpha$, $\beta$ és $\gamma =\pi -\alpha -\beta$ szögeket, amelyek alapján az $AX$, $BY$ és $CZ$ szakaszok egymáshoz képest beállíthatók.  $\square$
Az 1. tétel és a 2. tétel bizonyítása alapján világos, hogy az alábbi tétel feltételeit nem lehet könnyíteni.

 

3. tétel (Az arányösszeg-tétel megfordítása). Ha adott közös $O$ pontra illeszkedő $AX$, $BY$ és $CZ$ szakaszokra érvényes Euler $\left(1\right)$ formulája, valamint a $p=\frac{AO\cdot OX}{AX}$, $q=\frac{BO\cdot OY}{BY}$ és $r=\frac{CO\cdot OZ}{CZ}$ számok mindegyike kisebb a másik kettő összegénél, akkor az $AX$, $BY$ és $CZ$ szakaszokat el lehet forgatni $O$ körül úgy, hogy az $X$, $Y$, $Z$ pontok rendre az $ABC$ háromszög megfelelő oldalaira essenek.

 

Bizonyítás. Az egyszerűség kedvéért legyen $a=\frac{AO}{OX}$, $b=\frac{BO}{OY}$ és $c=\frac{CO}{OZ}$. A feltétel szerint

$\begin{array}{c}{\displaystyle \frac{1}{1+a}+\frac{1}{1+b}+\frac{1}{1+c}=1.}\end{array}$

(8)

Szerkesszünk egy olyan $PQR$ háromszöget, mely oldalainak hossza (a szokásos módon jelölve) $p$, $q$ és $r$. A csúcsoknál lévő szögek legyenek rendre $\alpha$, $\beta$ és $\gamma =\pi -\alpha -\beta$.
Forgassuk el az $AX$, $BY$ és $CZ$ szakaszokat úgy, hogy $ZOB\sphericalangle$ legyen $\alpha$, $XOC\sphericalangle$ legyen $\beta$ és $YOA\sphericalangle$ legyen $\gamma$. Eszerint

${\displaystyle \begin{array}{ccc}\hfill {\displaystyle q^2-2rq\text{cos}\alpha +r^2}& {\displaystyle =p^2\mathrm{,}}\hfill & \text{(<mn>9</mn>)}\\ \hfill {\displaystyle p^2-2rp\text{cos}\beta +r^2}& {\displaystyle =q^2\mathrm{,}}\hfill \\ \hfill {\displaystyle p^2-2qp\text{cos}\gamma +q^2}& {\displaystyle =r^2\mathrm{.}}\hfill \end{array}}$

Most igazoljuk, hogy a kialakult $ABC$ háromszög csúcsokkal szemközti oldalai rendre tartalmazzák az $X$, $Y$ és $Z$ pontokat.
Legyen $\widehat{X}=AX\cap BC$, $\widehat{Y}=BY\cap CA$ és $\widehat{Z}=CZ\cap AB$, továbbá $\widehat{a}=\frac{AO}{O\widehat{X}}$, $\widehat{b}=\frac{BO}{O\widehat{Y}}$ és $\widehat{c}=\frac{CO}{O\widehat{Z}}$. Az $ABC$ háromszögre is érvényes (1), így

$\begin{array}{c}{\displaystyle \frac{1}{1+\widehat{a}}+\frac{1}{1+\widehat{b}}+\frac{1}{1+\widehat{c}}=1}\end{array}$

(10)

adódik. Bevezetve a $\widehat{p}=\frac{AO\cdot O\widehat{X}}{A\widehat{X}}$, $\widehat{q}=\frac{BO\cdot O\widehat{Y}}{B\widehat{Y}}$ és $\widehat{r}=\frac{CO\cdot O\widehat{Z}}{C\widehat{Z}}$ jelöléseket, (7) és a szerkesztés menete alapján

${\displaystyle \begin{array}{ccc}\hfill {\displaystyle {\widehat{q}}^2-2\widehat{r}\widehat{q}\text{cos}\alpha +{\widehat{r}}^2}& {\displaystyle ={\widehat{p}}^2\mathrm{,}}\hfill & \text{(<mn>11</mn>)}\\ \hfill {\displaystyle {\widehat{p}}^2-2\widehat{r}\widehat{p}\text{cos}\beta +{\widehat{r}}^2}& {\displaystyle ={\widehat{q}}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle {\widehat{p}}^2-2\widehat{q}\widehat{p}\text{cos}\gamma +{\widehat{q}}^2}& {\displaystyle ={\widehat{r}}^2\mathrm{.}}\hfill \end{array}}$

Az (9) egyenleteket összevetve az (11) egyenletekkel, mivel mindkét egyenlethármas azonos szögű, tehát hasonló háromszögekre vonatkozik, adódik, hogy $\widehat{p}=\lambda p$, $\widehat{q}=\lambda q$ és $\widehat{r}=\lambda r$ valamely $\lambda >0$ számra. Tekintve a $p$, $q$, $r$ és $\widehat{p}$, $\widehat{q}$, $\widehat{r}$ definícióit, ebből $\frac{1}{1+\widehat{a}}=\frac{\lambda }{1+a}$, $\frac{1}{1+\widehat{b}}=\frac{\lambda }{1+b}$, és $\frac{1}{1+\widehat{c}}=\frac{\lambda }{1+c}$ adódik, amiből (8) és (10) összevetésével $\lambda =1$ következik. Eszerint $\widehat{a}=a$, $\widehat{b}=b$, és $\widehat{c}=c$, vagyis $\widehat{X}=X$, $\widehat{Y}=Y$, és $\widehat{Z}=Z$.
Ezzel a tételt bebizonyítottuk.  $\square$

 

3. Általánosítás helyett egy egyenlőtlenség

Belátható, hogy Euler arányösszeg-tétele igaz marad akkor is, ha a háromszög csúcsaiból kiinduló egyenesek metszéspontjáról csak annyit teszünk fel, hogy az nem esik a háromszög egyik oldalegyenesére se. Sőt, ezen általánosabb eset megfordítása is érvényben marad ha az $X$, $Y$, $Z$ pontoktól csak azt várjuk el, hogy a megfelelő oldalegyenesekre essenek. Ennek bizonyítását itt nem végezzük el, helyette egy Routh tételére ([1, 13.55], [11]) emlékeztető egyenlőtlenséget mutatunk.
Az arányösszeg-formulát tekintsük most az ekvivalens (4) alakjában. Ez a formula a három szakasz egy ponton áthaladása esetén érvényes. Ha a szakaszok páronként különböző $H$, $I$, $J$ pontokban metszik egymást, akkor is képezhetünk minden szakaszon arányt, ha a két metszéspont által meghatározott szakasz felezőpontját tekintjük új osztópontnak.

 

4. tétel. Legyenek $X$, $Y$, $Z$ az $ABC$ háromszög rendre $A$, $B$, $C$ csúccsal szemközti oldalainak pontjai, legyenek továbbá őket a szemközti csúcsokkal összekötő szakaszok metszéspontjai $H=AX\cap BY$, $I=BY\cap CZ$ és, $J=CZ\cap AX$. Végül legyenek ez utóbbiak által meghatározott $HIJ$ háromszög oldalfelező pontjai $K=\left(J+H\right)/2$, $L=\left(H+I\right)/2$ és $M=\left(I+J\right)/2$. Ekkor

$\begin{array}{c}{\displaystyle \frac{KX}{AX}+\frac{LY}{BY}+\frac{MZ}{CZ}\ge \mathrm{1,}}\end{array}$

(12)

ahol egyenlőség pontosan akkor áll fenn, ha $K=L=M$.

 

 

 

Bizonyítás. Rendre azonos alapú háromszögek területének arányait írhatjuk fel a következőképpen:

${\displaystyle \begin{array}{cccccc}\hfill {\displaystyle \frac{t\left(HBC\right)}{t\left(ABC\right)}}& {\displaystyle =\frac{HX}{AX}\mathrm{,}}\hfill & {\displaystyle \frac{t\left(JBC\right)}{t\left(ABC\right)}}\hfill & \hfill {\displaystyle =\frac{JX}{AX}\mathrm{,}}& {\displaystyle \frac{t\left(ICA\right)}{t\left(ABC\right)}}\hfill & {\displaystyle =\frac{IY}{BX}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{t\left(HCA\right)}{t\left(ABC\right)}}& {\displaystyle =\frac{HY}{BX}\mathrm{,}}\hfill & {\displaystyle \frac{t\left(JAB\right)}{t\left(ABC\right)}}\hfill & \hfill {\displaystyle =\frac{JZ}{CX}\mathrm{,}}& {\displaystyle \frac{t\left(IAB\right)}{t\left(ABC\right)}}\hfill & {\displaystyle =\frac{IZ}{CX}\mathrm{.}}\hfill \end{array}}$

Ezeket a 12 bal oldalának kétszeresébe helyettesítve kapjuk, hogy

${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle \frac{HX+JX}{AX}+\frac{IY+HY}{BY}+\frac{JZ+IZ}{CZ}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{t\left(HBC\right)}{t\left(ABC\right)}+\frac{t\left(JBC\right)}{t\left(ABC\right)}+\frac{t\left(ICA\right)}{t\left(ABC\right)}+\frac{t\left(HCA\right)}{t\left(ABC\right)}+\frac{t\left(JAB\right)}{t\left(ABC\right)}+\frac{t\left(IAB\right)}{t\left(ABC\right)}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{t\left(HBC\right)}{t\left(ABC\right)}+\frac{t\left(HCA\right)}{t\left(ABC\right)}+\frac{t\left(ICA\right)}{t\left(ABC\right)}+\frac{t\left(IAB\right)}{t\left(ABC\right)}+\frac{t\left(JBC\right)}{t\left(ABC\right)}+\frac{t\left(JAB\right)}{t\left(ABC\right)}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =1-\frac{t\left(HAB\right)}{t\left(ABC\right)}+1-\frac{t\left(IBC\right)}{t\left(ABC\right)}+1-\frac{t\left(JAC\right)}{t\left(ABC\right)}=3-\frac{t\left(ABC\right)-t\left(HIJ\right)}{t\left(ABC\right)}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =2+\frac{t\left(HIJ\right)}{t\left(ABC\right)}\mathrm{.}}\hfill \end{array}}$

Ezzel a tételünket bizonyítottuk.  $\square$

 

Hivatkozások

[1]	H. S. M. Coxeter, A geometriák alapjai, Műszaki Könyvkiadó, Budapest, 1973.

[2]	L. Euler, Geometrica et sphaerica quaedam, Memoires de lAcademie des Sciences de Saint-Petersbourg, 5 (1815), 96‐114; Opera Omnia Series 1, vol. XXVI, 344‐358; eredeti: http://eulerarchive.maa.org/docs/originals/E749.pdf; angol fordítás: http://eulerarchive.maa.org/Estudies/E749t.pdf.

[3]	A. J. Lexell, Solutio problematis geometrici ex doctrina sphaericorum, Acta academiae scientarum imperialis Petropolitinae, 5:1 (1784), 112‐126; http://www.17centurymaths.com/contents/euler/lexellone.pdf.

[4]	A. Papadopoulos and W. Su, On hyperbolic analogues of some classical theorems in spherical geometry, arXiv (2015), http://arxiv.org/abs/1409.4742.

[5]	B. Grünbaum and M. S. Klamkin, Euler's Ratio-Sum Theorem and Generalizations, Mathematics Magazine, 79:2 (Apr) (2006), 122‐130; http://www.jstor.org/stable/27642919.

[6]	B. Grünbaum, Cyclic ratio sums and products, Crux Mathematicorum, 24:1 (1998), 20‐25; https://cms.math.ca/crux/v24/n1/page20-25.pdf.

[7]	Á. Kurusa and J. Kozma, Euler's ratio-sum theorem revisited, Forum Geom., 19 (2019); http://forumgeom.fau.edu/FG2019volume19/FG2019index.html.

[8]	Á. Kurusa and J. Kozma, Euler's ratio-sum formula in projective-metric spaces, Beiträge zur Algebra und Geometrie, (2018); https://doi.org/10.1007/s13366-018-0422-6.

[9]	G. C. Shephard, Euler's Triangle Theorem, Crux Mathematicorum, 25:3  (1999), 148‐153; https://cms.math.ca/crux/v25/n3/page148-153.pdf.

[10]	C. E. Sandifer, 19th century Triangle Geometry (May 2006), How Euler did it, Math. Ass. Amer., 2007, 19‐27; http://eulerarchive.maa.org/hedi/HEDI-2006-05.pdf.

[11]	https://en.wikipedia.org/wiki/Routh's_theorem; Accessed 2019. március 8.

¹Ugyanez angol nyelven is elérhető, lásd [7].

²A [9] tanulmány igazolta, hogy amennyiben csak az (1) egyenletben szereplő arányok betartása fontos, akkor (1) elegendő: minden további feltétel nélkül van olyan háromszög, amelyben éppen az (1) egyenletben szereplő arányok lépnek fel. Sőt, a szerző megjegyzi, hogy egy ilyen háromszög minden affin képe is megteszi.