Cím:	A 2018. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldásai
Szerző(k):	Fleiner Tamás
Füzet:	2019/február, 67 - 70. oldal	PDF  |  MathML
Témakör(ök):	Matematika, Kürschák József (korábban Eötvös Loránd), Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   1. Az $ABC$ háromszög beírt köre a $BC$, a $CA$, illetve az $AB$ oldalt rendre az $A_1$, a $B_1$, illetve a $C_1$ pontban érinti, $A$-ból induló súlyvonala pedig az $M$ pontban metszi a $B_1{C}_1$ szakaszt. Mutassuk meg, hogy az $A_{1}M$ szakasz merőleges a $BC$ oldalra.   I. megoldás. Ha $|AB|=|AC|$, akkor az ábra szimmetrikus az $A$-ból induló magasságra, amely egyben súlyvonal is. Ezért az $A_1$ és az $M$ pont is ezen a szimmetriatengelyen fekszik, így az állítás triviális. A továbbiakban feltesszük, hogy $|AB|\ne |AC|$. Ekkor az $A$-ból induló szögfelező nem merőleges a $BC$ oldalra, tehát az $AB$-nek egy, a $BC$-re merőleges egyenesre vett tükörképe nem párhuzamos $AC$-vel. Legyen $K$ az $ABC$ háromszög beírt körének középpontja, és jelölje $A\text{'}$, $B\text{'}$ és $C_1\text{'}$ rendre az $A$, $B$, illetve $C_1$ pontoknak az $A_{1}K$ egyenesre vett tükörképét. Láttuk, hogy $AC$ és $A\text{'}B\text{'}$ nem párhuzamosak, ezért egyértelműen létezik az $AC$ és $A\text{'}B\text{'}$ egyeneseknek egy $P\text{'}$ metszéspontja. Legyen $P$ a $P\text{'}$-nek az $A_{1}K$-ra vett tükörképe, valamint jelölje $N$ a $PP\text{'}$ és $A_{1}K$ metszéspontját (1. ábra). 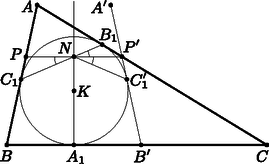    1. ábra   Ekkor $KNP\text{'}\sphericalangle ={90}^{\circ }$ a tükrözés miatt, illetve $K{B}_{1}P\text{'}\sphericalangle =K{C}_1\text{'}P\text{'}\sphericalangle ={90}^{\circ }$, hiszen $P\text{'}{B}_1$ és $P\text{'}{C}_1\text{'}$ a beírt kör érintői. Ezek szerint $K$, $N$, $B_1$, $P\text{'}$ és $C_1\text{'}$ egy $k$ körön vannak, konkrétan a $KP\text{'}$ Thálesz-körén. Ezen $k$ körnek $P\text{'}{B}_1$ és $P\text{'}{C}_1\text{'}$ egyenlő hosszúságú húrjai (mivel mindkét szakasz a beírt körnek ugyanabból a $P\text{'}$ külső pontból húzott érintője), tehát $k$-ban ugyanakkora kerületi szögek tartoznak hozzájuk: $B_{1}NP\text{'}\sphericalangle =C_1\text{'}NP\text{'}\sphericalangle =C_{1}NP\sphericalangle$; az utóbbi egyenlőség a tükrözés miatt igaz. Ezek szerint $N$ illeszkedik a $C_1{B}_1$ szakaszra. $BC\perp A_{1}K\perp PP\text{'}$ miatt $BC\parallel PP\text{'}$ és $|PN|=|P\text{'}N|$ a tükrözésből adódóan. Alkalmas, $A$-ból végzett középpontos hasonlóság tehát $PP\text{'}$-t $BC$-be és $N$-et a $BC$ szakasz felezőpontjába viszi. Ez pedig azt jelenti, hogy $N$ rajta van az $ABC$ háromszög $A$-ból induló súlyvonalán. Az $N$ pont tehát megegyezik a $B_1{C}_1$ szakasznak és az $ABC$ háromszög $A$-ból induló súlyvonalának metszéspontjával, $M$-mel, ahonnan $A_{1}M=A_{1}N\perp BC$ adódik. Nekünk pedig pontosan ezt kellett igazolunk.  $\square$   Az alábbiakban közöljük Egri Máté rendkívül szellemes megoldásának vázlatát is.   II. megoldás. Jelölje $Q$ az $ABC$ háromszög beírt körének $A_1$-gyel átellenes pontját, és legyenek rendre $E$ és $F$ a beírt körhöz $Q$-ban húzott (és $BC$-vel párhuzamos) érintőnek az $AB$ és $AC$ oldalakkal vett metszéspontjai (2. ábra). 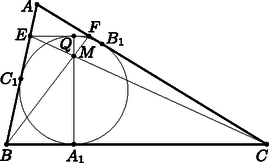    2. ábra   Azt fogjuk megmutatni, hogy az $M$ pont egyrészt megegyezik $EC$ és $BF$ metszéspontjával, másrészt, hogy illeszkedik az $A_{1}Q$ szakaszra. A konstrukció folytán $EBCF$ trapéz, így átlóinak metszéspontját a szárak metszéspontjával (azaz $A$-val) összekötő egyenes felezi az alapokat. Ez azt jelenti, hogy $EC$ és $BF$ metszéspontja illeszkedik az $A$-ból induló súlyvonalra. A továbbiakban a jól ismert Brianchon-tételre támaszkodunk, amely szerint egy érintőhatszög szemközti csúcsait összekötő három átló egy ponton halad át. A tételt abban az elfajuló esetben alkalmazzuk, amikor az érintőhatszög bizonyos csúcsai a hatszög beírt körén vannak. Ilyenformán az $E{C}_{1}BC{B}_{1}F$ elfajuló érintőhatszög fenti tulajdonsága alapján $C_1{B}_1$ tartalmazza $EC$ és $BF$ metszéspontját, amely ‐ mint láttuk ‐ az $A$-ból induló súlyvonalon van. Tehát $EC$ és $BF$ valóban az $M$ pontban metszik egymást. Az $EB{A}_{1}CFQ$ érintőhatszögre pedig az adódik, hogy $A_{1}Q$ is tartalmazza $M$-et. A feladat állítása innen közvetlenül adódik. $\square$   2. Legyenek ${\text{v}}_1\mathrm{,}{\text{v}}_2\mathrm{,}\text{...}\mathrm{,}{\text{v}}_n$ a térbeli derékszögű koordinátarendszer egész koordinátájú, páronként különböző, $p$ hosszúságú vektorai, ahol $p$ prímszám. Tegyük fel, hogy tetszőleges $1\le j<k\le n$ esetén van olyan $0<\ell <p$ egész szám, melyre a ${\text{v}}_j-\ell \cdot {\text{v}}_k$ vektor mindhárom koordinátája $p$-vel osztható. Igazoljuk, hogy $n\le 6$.   Megoldás. Ha $p=2$, akkor a $p$ hosszúságú, egész koordinátájú vektorok kizárólag a $\left(\pm p\mathrm{,0,0}\right)$, $\left(\mathrm{0,}\pm p\mathrm{,0}\right)$, $\left(\mathrm{0,0,}\pm p\right)$ vektorok lehetnek, amiből pontosan hat db van. A továbbiakban feltesszük tehát, hogy $p\ge 3$. Figyeljük meg, hogy ha valamelyik ${\text{v}}_j$ vektor mindhárom koordinátája $p$-vel osztható, akkor a feladatbeli feltétel szerint valamely $0<\ell <p$ esetén a ${\text{v}}_j-\ell \cdot {\text{v}}_k$ vektor mindhárom koordinátája osztható $p$-vel. Ekkor azonban az $\ell \cdot {\text{v}}_k$ vektornak, következésképp a ${\text{v}}_k$ vektornak is mindhárom koordinátája osztható $p$-vel, tehát a ${\text{v}}_1\mathrm{,}\text{...}\mathrm{,}{\text{v}}_n$ vektorok mindegyikére ugyanez igaz. Tekintettel arra, hogy a $p$ hosszúságú, $p$-vel osztható egész koordinátájú vektorok csupán hatfélék lehetnek (konkrétan $\left(\pm p\mathrm{,0,0}\right)$, $\left(\mathrm{0,}\pm p\mathrm{,0}\right)$, $\left(\mathrm{0,0,}\pm p\right)$), ezért feltehetjük, hogy a ${\text{v}}_j$ vektorok egyikének sem osztható mindhárom koordinátája $p$-vel. A feladatbeli feltétel miatt tetszőleges $1\le j<k\le n$ esetén létezik olyan $p\nmid \ell$ egész, amelyre az $\text{u}=\left({\text{v}}_j-\ell \cdot {\text{v}}_k\right)/p$ vektor mindhárom koordinátája egész. Ekkor (az $\text{x}$ és $\text{y}$ vektorok skaláris szorzatát $\left(\text{x}\mathrm{,}\text{y}\right)$-nal jelölve) ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {|{\text{v}}_j|}^2}& {\displaystyle =\left({\text{v}}_j\mathrm{,}{\text{v}}_j\right)=\left(p\cdot \text{u}+\ell \cdot {\text{v}}_k\mathrm{,}p\cdot \text{u}+\ell \cdot {\text{v}}_k\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =p^2\cdot \left(\text{u}\mathrm{,}\text{u}\right)+2p\ell \cdot \left(\text{u}\mathrm{,}{\text{v}}_k\right)+{\ell }^2\cdot \left({\text{v}}_k\mathrm{,}{\text{v}}_k\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =p^2\cdot {|\text{u}|}^2+2p\ell \cdot \left(\text{u}\mathrm{,}{\text{v}}_k\right)+{\ell }^2\cdot {|{\text{v}}_k|}^2\mathrm{,}}\hfill \end{array}}$ azaz $\begin{array}{c}{\displaystyle -2p\ell \cdot \left(\text{u}\mathrm{,}{\text{v}}_k\right)=p^2\cdot {|\text{u}|}^2+{\ell }^2\cdot {|{\text{v}}_k|}^2-{|{\text{v}}_j|}^2=p^2\cdot {|\text{u}|}^2+{\ell }^2\cdot p^2-p^2=p^2\left({|\text{u}|}^2+{\ell }^2-1\right)\mathrm{.}}\end{array}$ Mivel $p>2$ és ${|\text{u}|}^2=\left(\text{u}\mathrm{,}\text{u}\right)$ egész, ezért a fenti egyenlőség bal oldala is $p^2$ többszöröse, tehát $p\mid \left(\text{u}\mathrm{,}{\text{v}}_k\right)$. Ekkor ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \left({\text{v}}_j\mathrm{,}{\text{v}}_k\right)}& {\displaystyle =\left(p\cdot \text{u}+\ell \cdot {\text{v}}_k\mathrm{,}{\text{v}}_k\right)=p\left(\text{u}\mathrm{,}{\text{v}}_k\right)+\ell \left({\text{v}}_k\mathrm{,}{\text{v}}_k\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =p\left(\text{u}\mathrm{,}{\text{v}}_k\right)+\ell \cdot {|{\text{v}}_k|}^2=p\left(\text{u}\mathrm{,}{\text{v}}_k\right)+\ell \cdot p^2\mathrm{,}}\hfill \end{array}}$ így $p\mid \left(\text{u}\mathrm{,}{\text{v}}_k\right)$ okán $p^2\mid \left({\text{v}}_j\mathrm{,}{\text{v}}_k\right)$. Azonban $|\left({\text{v}}_j\mathrm{,}{\text{v}}_k\right)|\le |{\text{v}}_j|\cdot |{\text{v}}_k|=p^2$ miatt $\left({\text{v}}_j\mathrm{,}{\text{v}}_k\right)$ csak $\pm p^2$ vagy $0$ lehet. Ezért ha ${\text{v}}_j$ és ${\text{v}}_k$ nem párhuzamosak, akkor bizonyosan merőlegesek egymásra. Azt kaptuk tehát, hogy a ${\text{v}}_1\mathrm{,}{\text{v}}_2\mathrm{,}\text{...}\mathrm{,}{\text{v}}_n$ vektorok meghatározta irányok páronként merőlegesek, ezért legfeljebb három ilyen irány lehetséges. Minthogy az azonos irányt meghatározó vektorok egymás ellentettjei, ezért minden irányt legfeljebb két vektor határoz meg, innen pedig közvetlenül adódik a bizonyítandó $n\le 6$ állítás.    $\square$   Megjegyzés. Ha $p=k^2+k+1$ valamely $k$ pozitív egészre, akkor megadható hat olyan vektor, amelyek teljesítik a feladatbeli követelményeket, és egyikük sem párhuzamos a koordinátatengelyekkel. Könnyű ellenőrizni, hogy például a $\left(k\mathrm{,}k+\mathrm{1,}k\left(k+1\right)\right)$, $\left(k+\mathrm{1,}-k\left(k+1\right)\mathrm{,}k\right)$, illetve $\left(-k\left(k+1\right)\mathrm{,}-k\mathrm{,}k+1\right)$ ilyen vektorhármast alkot. Általánosságban az igaz, hogy a $2$ és az $5$ kivételével minden $p$ prímre létezik hat vektor a fenti tulajdonsággal. A részletekért ld. az A. 744., ehavi számunkban kitűzött feladatot.   3. A $k$ utcából álló Aprajafalván $k\left(n-1\right)+1$ klub működik, mindegyik tagsága $n$ törpöt számlál. Egy törp több klubnak is tagja lehet, és két törp bizonyosan ismeri egymást, ha klubtársak vagy ha ugyanabban az utcában laknak. Igazoljuk, hogy kiválasztható $n$ különböző klub és ezeknek egy-egy tagja úgy, hogy ez az $n$ tag páronként különböző legyen és közülük bármely kettő ismerje egymást.   Megoldás. Legyenek a klubok $K_1\mathrm{,}{K}_2\mathrm{,}\text{...}$ és válasszunk sorra minden klubból egy-egy képviselőt azzal a megszorítással, hogy minden törp legfeljebb egy klubot képviselhet. Ha e választások során a $K_i$ klubból nem tudunk képviselőt választani, akkor az azért van, mert $K_i$ minden egyes tagja (akik persze páronként ismerik egymást) már képvisel egy-egy különböző klubot, ezért kész vagyunk. Ha azonban mind a $k\left(n-1\right)+1$ klubból sikerül különböző képviselőt választani, akkor a skatulya-elv miatt közülük $n$ törp ugyanabban az utcában lakik, és ezért ismerik egymást.  $\square$