Cím:	Megoldásvázlatok a 2018/9. sz. emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Szoldatics József
Füzet:	2019/január, 9 - 19. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Oldjuk meg a valós számok halmazán a következő egyenletet: $\begin{array}{c}{\displaystyle \text{log}{}_{2^x+1}\left(2^{x+1}+5\right)=2.}\end{array}$ (6 pont) $b)$ A LOTTÓ $(90$ számból $5$ húzása$)$ megváltoztatására készülnek. Két javaslat van. Az egyik $90$-ből $4$ szám húzását javasolva a régi módon, a másik meg $45$ számból $4$ húzását javasolja a sorrend figyelembe vételével, de ez lehetővé tenné, hogy ugyanazt a számot többször is ki lehessen húzni, azaz a már húzott számot ismét visszatennék. Azt akarnák elfogadni, amelyik játék esetében kevesebb az esély a telitalálatra. Zsebszámológép nélkül (!) határozzuk meg, hogy melyiket válasszák.   (6 pont)   Megoldás. $a)$ Mivel az exponenciális függvény mindig pozitív, ezért $2^x+1>1$, tehát a logaritmus alapszáma pozitív és nem egyenlő 1-gyel, valamint $2^{x+1}+5>5$, tehát a logaritmizálandó kifejezés is pozitív. Az egyenletünk minden valós számra értelmezett. Rendezzük az egyenletünket, közben használjuk a logaritmus definícióját, valamint az exponenciális függvény monoton tulajdonságát: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{log}{}_{2^x+1}\left(2^{x+1}+5\right)}& {\displaystyle =\mathrm{2,}}\hfill \\ \hfill {\displaystyle 2^{x+1}+5}& {\displaystyle ={\left(2^x+1\right)}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle 2\cdot 2^x+5}& {\displaystyle =2^{2x}+2\cdot 2^x+\mathrm{1,}}\hfill \\ \hfill {\displaystyle 4}& {\displaystyle =2^{2x}\mathrm{,}}\hfill \\ \hfill {\displaystyle 2^2}& {\displaystyle =2^{2x}\mathrm{,}}\hfill \\ \hfill {\displaystyle 2}& {\displaystyle =2x\mathrm{,}}\hfill \\ \hfill {\displaystyle 1}& {\displaystyle =x\mathrm{.}}\hfill \end{array}}$ Az ellenőrzés a kapott gyököt jónak találja: $\begin{array}{c}{\displaystyle \text{log}{}_{2^1+1}\left(2^{1+1}+5\right)=\text{log}{}_{3}9=2.}\end{array}$ $b)$ Az első verzió szerint 90 számból 4 számot húznak a sorrend figyelembe vétele nélkül, ez megtehető $\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{90}{4}\right)=\frac{90!}{4!\cdot 86!}=\frac{90\cdot 89\cdot 88\cdot 87}{1\cdot 2\cdot 3\cdot 4}}\end{array}$ módon. A másik esetben 45 számból 4 szám húzása a javaslat, a húzott számok sorrendjének a figyelembe vételével és a már húzott számok visszatételével. Ez megtehető ${45}^4$ módon. Induljunk ki az első módon húzott esetre kapott végeredményből és végezzünk becslést: $\begin{array}{c}{\displaystyle \frac{90\cdot 89\cdot 88\cdot 87}{1\cdot 2\cdot 3\cdot 4}=\frac{90}{2}\cdot \frac{89}{2}\cdot \frac{88}{2}\cdot \frac{87}{3}=45\cdot \mathrm{44,5}\cdot 44\cdot 29<45\cdot 45\cdot 45\cdot 45={45}^4\mathrm{.}}\end{array}$ A második módon többféle húzás lehetséges, a telitalálat valószínűsége kisebb. Tehát ezt célszerű választani.   2. $a)$ Oldjuk meg a valós számok halmazán a következő egyenletet, ahol $p$ valós paraméter: $\begin{array}{c}{\displaystyle 3x+2p=5\sqrt[]{px}\mathrm{.}}\end{array}$ (7 pont) $b)$ Egy négyszögnek, mely egyidejűleg érintő és húrnégyszög is, az egyik oldala 5 cm és valamelyik oldaltól kezdve pozitív körbejárás szerint véve az oldalakat mértani sorozat elemeit kapjuk. Mekkora a másik három oldal és milyen négyszögről van szó?  (6 pont)   Megoldás. $a)$ A gyökjel alatt nem állhat negatív kifejezés, ezért a megoldhatóság feltétele: $px\ge 0$. I. eset: $p<0$. Ekkor a feltételből adódik, hogy $x\le 0$ lehet, de így az egyenlet bal oldala ($3x+2p$) negatív, míg a jobb oldala nem negatív, tehát ekkor nincs megoldás. II. eset: $p=0$. Ekkor egyenletünk $3x=0$ alakot vesz fel, aminek az $x=0$ a megoldása. III. eset: $p>0$, ekkor a feltételből adódik, hogy $x\ge 0$, így az egyenlet mindkét oldala pozitív, ezért négyzetre emeljük és rendezzük: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 3x+2p}& {\displaystyle =5\sqrt[]{px}\mathrm{,}}\hfill \\ \hfill {\displaystyle {\left(3x+2p\right)}^2}& {\displaystyle =25px\mathrm{,}}\hfill \\ \hfill {\displaystyle 9x^2-13px+4p^2}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle x_{\mathrm{1,2}}=\frac{13p\pm \sqrt[]{{\left(13p\right)}^2-4\cdot 9\cdot 4p^2}}{18}}& {\displaystyle =\frac{13p\pm 5p}{18}\mathrm{,}}\hfill \\ \hfill {\displaystyle x_1=p;x_2}& {\displaystyle =\frac{4}{9}p\mathrm{.}}\hfill \end{array}}$ $b)$ Az oldalak mértani sorozatot alkotnak, ezért jelöljük ezen sorozat első tagját $a$-val ($a>0$), és a hányadosát $q$-val ($q>0$). Ekkor az oldalak rendre $a$, $aq$, $a{q}^2$, $a{q}^3$ lesznek. Mivel érintőnégyszögről van szó, ezért a szemben levő oldalak összege megegyezik, azaz ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a+a{q}^2}& {\displaystyle =aq+a{q}^3\mathrm{,}}\hfill \\ \hfill {\displaystyle a+a{q}^2-aq-a{q}^3}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle a\left(1+q^2-q-q^3\right)}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle a\left(1+q^2-q\left(1+q^2\right)\right)}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle a\left(1-q\right)\left(1+q^2\right)}& {\displaystyle =0.}\hfill \end{array}}$ Itt $a>0$ és $1+q^2>0$, ezért $1-q=0$, azaz $q=1$, ekkor a négyszög minden oldala megegyezik. Mivel az egyik oldal 5 cm, ezért minden oldala ugyanekkora, tehát rombuszról van szó. A másik feltétel szerint húrnégyszög is, azaz a rombuszok között keresünk ilyen négyszöget, ami csak négyzet lehet.   3. $a)$ Oldjuk meg a valós számok halmazán a következő egyenletrendszert: $\begin{array}{c}{\displaystyle \{{\displaystyle \begin{array}{cc}\hfill {\displaystyle {\displaystyle \frac{x}{y}}-1}& {\displaystyle =1-{\displaystyle \frac{y}{x}}\mathrm{,}}\hfill \\ \hfill {\displaystyle x^8+2y^6}& {\displaystyle =x^6+2y^8\mathrm{.}}\hfill \end{array}}}\end{array}$ (6 pont) $b)$ Adjuk meg az összes $p$ pozitív prímszámot, melyre a $\begin{array}{c}{\displaystyle 4x^2-4\left(2p+1\right)x+\left(4p^2-p\right)=0}\end{array}$ egyenlet gyökeinek különbsége egész szám.  (7 pont)   Megoldás. $a)$ Mivel tört szerepel az egyenletekben, ezért $x\ne 0$ és $y\ne 0$ kell a megoldhatósághoz. Rendezzük az első egyenletet: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{x}{y}-1}& {\displaystyle =1-\frac{y}{x}\mathrm{,}}\hfill \\ \hfill {\displaystyle x^2-xy}& {\displaystyle =xy-y^2\mathrm{,}}\hfill \\ \hfill {\displaystyle x^2-2xy+y^2}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle {\left(x-y\right)}^2}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle x}& {\displaystyle =y\mathrm{.}}\hfill \end{array}}$ Ezt a második egyenletbe helyettesítve: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x^8+2y^6}& {\displaystyle =x^6+2y^8\mathrm{,}}\hfill \\ \hfill {\displaystyle x^8+2x^6}& {\displaystyle =x^6+2x^8\mathrm{,}}\hfill \\ \hfill {\displaystyle 0}& {\displaystyle =x^8-x^6\mathrm{,}}\hfill \\ \hfill {\displaystyle 0}& {\displaystyle =x^6\left(x^2-1\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle 0}& {\displaystyle =x^6\left(x-1\right)\left(x+1\right);}\hfill \\ \hfill {\displaystyle x_1}& {\displaystyle =\mathrm{0,}{x}_2=\mathrm{1,}{x}_3=-1.}\hfill \end{array}}$ $x_1$ nem jó megoldás a kikötés miatt, a másik kettő pedig az $M_1\left(1;1\right)$ és $M_2\left(-1;-1\right)$ megoldásokat szolgáltatja, amit az ellenőrzés jónak is talál. $b)$ Vizsgáljuk meg, hogy egyáltalán mikor van az egyenletnek valós megoldása. A diszkriminánst felírva: $\begin{array}{c}{\displaystyle D={\left[4\left(2p+1\right)\right]}^2-4\cdot 4\cdot \left(4p^2-p\right)=80p+16>\mathrm{16,}}\end{array}$ ami mindig pozitív a feltételek miatt, tehát az egyenletnek minden esetben van két különböző valós gyöke. A Viéte-formulákat felírva: $\begin{array}{c}{\displaystyle x_1+x_2=2p+\mathrm{1,}{x}_1{x}_2=\frac{4p^2-p}{4}\mathrm{.}}\end{array}$ Keressük a gyökök különbségének a négyzetét a következő azonosság alapján: $\begin{array}{c}{\displaystyle {\left(x_1-x_2\right)}^2={\left(x_1+x_2\right)}^2-4x_1{x}_2={\left(2p+1\right)}^2-4\cdot \frac{4p^2-p}{4}=5p+1.}\end{array}$ Innen a gyökök különbsége $\begin{array}{c}{\displaystyle |x_1-x_2|=\sqrt[]{5p+1}\mathrm{.}}\end{array}$ Ha ez egész, akkor az $5p+1$ kifejezés egy egész szám négyzete. A továbbiakban meg kell oldanunk az $5p+1=a^2$ egyenletet, ahol $a\in \text{N}$. Ezt átrendezve: $\begin{array}{c}{\displaystyle 5p=a^2-1=\left(a-1\right)\left(a+1\right)\mathrm{.}}\end{array}$ Mivel $5$ is és $p$ is prím, ezért a következő esetek vannak: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccccc}\hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo stretchy="false">-</mo><mn>1</mn></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo stretchy="false">+</mo><mn>1</mn></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>p</mi></math> }}\hfill & {\displaystyle }\hfill \\ \hfill {\displaystyle \text{1 }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>5</mn><mi>p</mi></math> }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ ─ }}\hfill & {\displaystyle }\hfill \\ \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>p</mi></math> }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill & {\displaystyle \text{ megoldás, <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>p</mi><mo stretchy="false">=</mo><mn>7</mn></math> }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>p</mi></math> }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & {\displaystyle \text{ megoldás, <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>p</mi><mo stretchy="false">=</mo><mn>3</mn></math> }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>5</mn><mi>p</mi></math> }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ ─ }}\hfill \end{array}}}\end{array}$ Ha $p=3$, akkor az egyenlet $4x^2-28x+33=0$; aminek a gyökei $x_1=\frac{11}{2}$ és $x_2=\frac{3}{2}$; amelyek különbsége $x_1-x_2=4$ egész. Ha $p=7$, akkor az egyenlet $4x^2-60x+189=0$; aminek a gyökei $x_1=\frac{21}{2}$ és $x_2=\frac{9}{2}$; amelyek különbsége $x_1-x_2=6$ egész.   4. $a)$ Oldjuk meg a valós számok halmazán a következő egyenletet: $\begin{array}{c}{\displaystyle \text{sin}x+\sqrt[]{3}\cdot \text{cos}x=4\cdot \text{sin}x\cdot \text{cos}x\mathrm{.}}\end{array}$ (7 pont) $b)$ Mekkora területet zárnak be az $y=x$ egyenes és az $y=x^3-9x^2+9x$ görbe?   (6 pont)   Megoldás. $a)$ Rendezzük a megadott egyenletet: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{sin}x+\sqrt[]{3}\cdot \text{cos}x}& {\displaystyle =4\cdot \text{sin}x\cdot \text{cos}x\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{1}{2}\cdot \text{sin}x+\frac{\sqrt[]{3}}{2}\cdot \text{cos}x}& {\displaystyle =2\cdot \text{sin}x\cdot \text{cos}x\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{1}{2}\cdot \text{sin}x+\frac{\sqrt[]{3}}{2}\cdot \text{cos}x}& {\displaystyle =\text{sin}2x;}\hfill \\ \hfill {\displaystyle \text{cos}\frac{\pi }{3}=\frac{1}{2}\mathrm{,}\text{sin}\frac{\pi }{3}}& {\displaystyle =\frac{\sqrt[]{3}}{2}\mathrm{,}\text{így}}\hfill \\ \hfill {\displaystyle \text{cos}\frac{\pi }{3}\cdot \text{sin}x+\text{sin}\frac{\pi }{3}\cdot \text{cos}x}& {\displaystyle =\text{sin}2x\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{sin}\left(x+\frac{\pi }{3}\right)}& {\displaystyle =\text{sin}2x\mathrm{.}}\hfill \end{array}}$ Mind a két oldalon sinus függvény áll, ezért ezek egyenlőségére 2 eset van. I. eset: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2x}& {\displaystyle =x+\frac{\pi }{3}+2k\pi \mathrm{,}k\in \text{Z}\mathrm{,}}\hfill \\ \hfill {\displaystyle x}& {\displaystyle =\frac{\pi }{3}+2k\pi \mathrm{.}}\hfill \end{array}}$ II. eset: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2x}& {\displaystyle =\pi -\left(x+\frac{\pi }{3}\right)+2k\pi \mathrm{,}k\in \text{Z}\mathrm{,}}\hfill \\ \hfill {\displaystyle 3x}& {\displaystyle =\frac{2\pi }{3}+2k\pi \mathrm{,}}\hfill \\ \hfill {\displaystyle x}& {\displaystyle =\frac{2\pi }{9}+\frac{2}{3}k\pi \mathrm{.}}\hfill \end{array}}$ Az ellenőrzés jónak találja a megadott gyököket. $b)$ A bezárt területhez szükségünk van a metszéspontokra: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x^3-9x^2+9x}& {\displaystyle =x\mathrm{,}}\hfill \\ \hfill {\displaystyle x^3-9x^2+8x}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle x\left(x^2-9x+8\right)}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle x\left(x-1\right)\left(x-8\right)}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle x_1=\mathrm{0,}{x}_2}& {\displaystyle =\mathrm{1,}{x}_3=8.}\hfill \end{array}}$     A keresett terület: $\begin{array}{c}{\displaystyle t=|\underset{0}{\overset{1}{\int }}\left(\left(x^3-9x^2+9x\right)-x\right)\text{d}x|+|\underset{1}{\overset{8}{\int }}\left(\left(x^3-9x^2+9x\right)-x\right)\text{d}x|\mathrm{.}}\end{array}$ Kiszámítva a két integrált: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle t_1}& {\displaystyle =\underset{0}{\overset{1}{\int }}\left(\left(x^3-9x^2+9x\right)-x\right)\text{d}x=\underset{0}{\overset{1}{\int }}\left(x^3-9x^2+8x\right)\text{d}x={\left[\frac{x^4}{4}-3x^3+4x^2\right]}_0^1=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\left(\frac{1^4}{4}-3\cdot 1^3+4\cdot 1^2\right)-\left(\frac{0^4}{4}-3\cdot 0^3+4\cdot 0^2\right)=\frac{5}{4}-0=\frac{5}{4}}\hfill \end{array}}$ és ${\displaystyle \begin{array}{cc}\hfill {\displaystyle t_2}& {\displaystyle =\underset{1}{\overset{8}{\int }}\left(\left(x^3-9x^2+9x\right)-x\right)\text{d}x=\underset{1}{\overset{8}{\int }}\left(x^3-9x^2+8x\right)\text{d}x={\left[\frac{x^4}{4}-3x^3+4x^2\right]}_1^8=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\left(\frac{8^4}{4}-3\cdot 8^3+4\cdot 8^2\right)-\left(\frac{1^4}{4}-3\cdot 1^3+4\cdot 1^2\right)=-256-\frac{5}{4}=-\frac{1029}{4}\mathrm{.}}\hfill \end{array}}$ A kapott negatív érték azt jelzi, hogy a két függvény közül az $y=x$ a ,,nagyobb'' ezen az intervallumon. A keresett terület tehát $\begin{array}{c}{\displaystyle t=\left|\frac{5}{4}\right|+\left|-\frac{1029}{4}\right|=\frac{1034}{4}\mathrm{.}}\end{array}$   II. 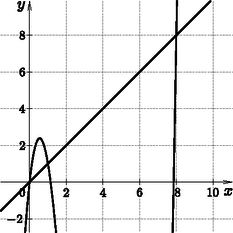rész     5. Az $y=x^3-6x^2+15x+c$ függvény egyik érintőjének egyenlete $y=6x-5$. Mekkora a $c$ értéke?  (16 pont)   Megoldás. Az érintő egyenletéből leolvasható, hogy meredeksége $m=6$. Egy görbéhez húzott érintő meredekségét a görbe első deriváltja szolgáltatja. $y\text{'}=3x^2-12x+15$ a függvényünk első deriváltja. Olyan pontot kell keresnünk, amely pontban a derivált felvett értéke 6, vagyis az $\begin{array}{c}{\displaystyle y\text{'}=3x^2-12x+15=6}\end{array}$ egyenletet kell megoldanunk. Ennek gyökei $x_1=1$ és $x_2=3$, azaz két lehetséges érintési pontot kaptunk, amely esetén a függvény és az adott érintő érinteni tudják egymást. I. eset: Érintési pont $x=1$. Ekkor az érintő átmegy az $M\left(1;1\right)$ ponton (az $y=6x-5$ egyenletből számolva), tehát a függvénynek is itt kell átmennie, azaz $\begin{array}{c}{\displaystyle 1^3-6\cdot 1^2+15\cdot 1+c=\mathrm{1,}}\end{array}$ innen $c=-9$. II. eset: Érintési pont $x=3$. Ekkor az érintő átmegy a $M\left(3;13\right)$ ponton (az $y=6x-5$ egyenletből számolva), tehát a függvénynek is itt kell átmennie, azaz $\begin{array}{c}{\displaystyle 3^3-6\cdot 3^2+15\cdot 3+c=\mathrm{13,}}\end{array}$ innen $c=-5$.   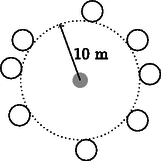6. A rajz szerint egy 10 m sugarú kör közepén állunk puskával a kézben, amit $8$ darab, 1 m sugarú tölgyfa vesz körbe nem egyenletesen elhelyezkedve (a rajz nem a valós elhelyezkedést mutatja). Véletlenszerűen $5$ lövést leadva mekkora annak a valószínűsége, hogy legalább $3$ lövés kijut a ,,fa ketrecből''?  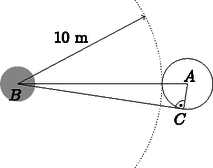(16 pont)       Megoldás. Tekintsünk csak 1 fát az ábrán látható módon. Legyen a fa középpontja $A$, a mi helyünk $B$. Húzzunk érintőt a fához, az érintési pont legyen $C$, ahol derékszög van. Ekkor ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{sin}ABC\sphericalangle }& {\displaystyle =\frac{1}{11}\mathrm{,}}\hfill \\ \hfill {\displaystyle ABC\sphericalangle }& {\displaystyle \approx 5\mathrm{,}{216}^{\circ }\mathrm{.}}\hfill \end{array}}$     Ebből következik, hogy a $B$ pontból a fa $2\cdot ABC\sphericalangle =10\mathrm{,}{432}^{\circ }$ szögben látszik. Tehát 1 fa eltalálási valószínűsége: $\begin{array}{c}{\displaystyle P\left(\text{1 fa talál}\right)=\frac{10\mathrm{,}432}{360}\mathrm{.}}\end{array}$ Nem ismerjük a fák elhelyezkedését, de 2 fa egyidejű találata lehetetlen esemény, egymást kizárják, a valószínűsége 0. Így annak a valószínűsége, hogy valamelyik fát eltaláljuk: $\begin{array}{c}{\displaystyle P\left(\text{fa találat}\right)=10\cdot P\left(\text{1 fa talál}\right)=\frac{104\mathrm{,}32}{360}\mathrm{.}}\end{array}$ Az egyszerűség kedvéért jelöljük ezt az értéket $p$-vel. A feladatunk a $P\left(\text{legalább 3 kijut az 5-ből}\right)$ valószínűség kiszámítása: $\begin{array}{c}{\displaystyle P\left(\text{legalább 3 kijut}\right)=P\left(\text{2 fa találat}\right)+P\left(\text{1 fa találat}\right)+P\left(\text{0 fa találat}\right)\mathrm{.}}\end{array}$ A pontosan 2 fa találat valószínűsége: $\left(\genfrac{}{}{0ex}{}{5}{2}\right)p^2{\left(1-p\right)}^3$. A pontosan 1 fa találat valószínűsége: $\left(\genfrac{}{}{0ex}{}{5}{1}\right)p^1{\left(1-p\right)}^4$. A pontosan 0 fa találat valószínűsége: $\left(\genfrac{}{}{0ex}{}{5}{0}\right)p^0{\left(1-p\right)}^5$. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle P\left(\text{legalább 3 kijut}\right)}& {\displaystyle =\left(\genfrac{}{}{0ex}{}{5}{2}\right)p^2{\left(1-p\right)}^3+\left(\genfrac{}{}{0ex}{}{5}{1}\right)p^1{\left(1-p\right)}^4+\left(\genfrac{}{}{0ex}{}{5}{0}\right)p^0{\left(1-p\right)}^5\mathrm{,}}\hfill \\ \hfill {\displaystyle P\left(\text{legalább 3 kijut}\right)}& {\displaystyle =85\mathrm{,}01\%\text{<span style="font-weight: normal;font-style: normal;">(2 tizedesre kerekítve).</span>}}\hfill \end{array}}$   7. Kugli játékhoz könnyen boruló bábut terveztünk. A rajz a keresztmetszeti képét ábrázolja. Veszünk egy $R=30$ cm sugarú gömböt, amiből kivágunk egy a gömb középpontjából induló kúpot úgy, hogy a gömb felületén egy $225\pi {\text{cm}}^2$ felületdarabot vágunk ki. Ezután egy $r=5$ cm sugarú gömböt teszünk a csúcsra úgy, hogy a kis gümb középpontja pont a csúcsra illeszkedjék (persze, előtte a szükséges lyukat kivágjuk). Mekkora az így kapott test térfogata?  (16 pont)       Megoldás. A nagy gömb felszíne $\begin{array}{c}{\displaystyle A=4\cdot {30}^2\cdot \pi =3600\pi \left({\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^2\right)\mathrm{.}}\end{array}$ A kivágott kúp ebből $225\pi {\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^2$ területet metsz ki, ami a teljes felszín $\begin{array}{c}{\displaystyle \frac{225\pi }{3600\pi }=\frac{1}{16}}\end{array}$ része. Tehát a kúp térfogatának is az $1/16$ részét vágjuk ki: $\begin{array}{c}{\displaystyle V_1=\frac{1}{16}\cdot \frac{4}{3}\cdot {30}^3\pi =2250\pi \left({\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^3\right)\mathrm{.}}\end{array}$ A kúpra rárakott kicsi gömb hasonló az eredetihez (két gömb mindig hasonló), így a vágási hányad is, de itt a $15/16$-od rész marad meg, azaz $\begin{array}{c}{\displaystyle V_2=\frac{15}{16}\cdot \frac{4}{3}\cdot 5^3\pi =\frac{625}{4}\pi \left({\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^3\right)\mathrm{.}}\end{array}$ Így a kugli térfogata: $\begin{array}{c}{\displaystyle V=V_1+V_2=2250\pi +\frac{625}{4}\pi =\frac{9625}{4}\pi \approx 7559\mathrm{,}46{\text{cm}}^3\mathrm{.}}\end{array}$   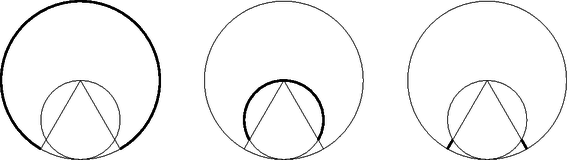8. Egy nyakláncra medált terveztünk, melyet a rajz mutat, ahol a medált a vastag vonalak határolják. A nagy kör sugara $R=4$ cm, a kicsi kör belülről érinti a nagy kört és sugara $r=2$ cm, amit kivágunk. Hogy ne legyen hegyes a medál, ezért a nagy kör középpontjából szimmetrikusan ${60}^{\circ }$ szög szögtartományában levő részeket is levágjuk. Mekkora a keletkezett medál kerülete, területe?   (16 pont)       Megoldás. A keresett kerület 3 részből áll össze:     Az első rész a nagy kör kerületének az öthatoda, hiszen ${60}^{\circ }$-os középponti szögnyi kerületet vágunk ki: $\begin{array}{c}{\displaystyle k_1=\frac{5}{6}\cdot 2\cdot 4\cdot \pi =\frac{20}{3}\pi \left(\text{<span style="font-weight: normal;font-style: normal;">cm</span>}\right)\mathrm{.}}\end{array}$ A második rész a kis kör kerületének a kétharmada, hiszen a ${60}^{\circ }$ kerületi szög ebben a körben, és így a középponti szög ${120}^{\circ }$, tehát ${120}^{\circ }$-os középponti szögnyi kerületet vágunk ki: $\begin{array}{c}{\displaystyle k_2=\frac{2}{3}\cdot 2\cdot 2\cdot \pi =\frac{8}{3}\pi \left(\text{<span style="font-weight: normal;font-style: normal;">cm</span>}\right)\mathrm{.}}\end{array}$ A harmadik rész pedig két kis szakasz, melyek hosszának meghatározásához a nagy kör sugarából ki kell vonni a kis kör ${120}^{\circ }$-os középponti szögéhez tartozó húrját: $\begin{array}{c}{\displaystyle k_3=2\left(4-2\cdot 2\text{sin}{60}^{\circ }\right)=2\left(4-2\cdot 2\cdot \frac{\sqrt[]{3}}{2}\right)=2\left(4-2\sqrt[]{3}\right)=8-4\sqrt[]{3}\left(\text{<span style="font-weight: normal;font-style: normal;">cm</span>}\right)\mathrm{.}}\end{array}$ A medál kerülete: $\begin{array}{c}{\displaystyle k=k_1+k_2+k_3=\frac{20}{3}\pi +\frac{8}{3}\pi +8-4\sqrt[]{3}=\frac{28}{3}\pi +8-4\sqrt[]{3}\left(\text{<span style="font-weight: normal;font-style: normal;">cm</span>}\right)\mathrm{,}}\end{array}$ ami két tizedesjegyre kerekítve: $\begin{array}{c}{\displaystyle k=\frac{28}{3}\pi +8-4\sqrt[]{3}\approx 30\mathrm{,}39\text{cm}\mathrm{.}}\end{array}$ A keresett területet két rész különbségeként állítjuk elő:     Az első rész a nagy kör öthatod része: $\begin{array}{c}{\displaystyle t_1=\frac{5}{6}\cdot 4^2\cdot \pi =\frac{40}{3}\pi \left({\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^2\right)\mathrm{.}}\end{array}$ A második rész pedig a kis kör területéből kivont szabályos háromszög különbségének a kétharmada: $\begin{array}{c}{\displaystyle t_2=\frac{2}{3}\left(2^2\cdot \pi -\frac{{\left(2\sqrt[]{3}\right)}^2\cdot \text{sin}{60}^{\circ }}{2}\right)=\frac{8}{3}\pi -2\sqrt[]{3}\left({\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^2\right)\mathrm{.}}\end{array}$ A medál területe: $\begin{array}{c}{\displaystyle t=t_1-t_2=\frac{40}{3}\pi -\left(\frac{8}{3}\pi -2\sqrt[]{3}\right)=\frac{32}{3}\pi +2\sqrt[]{3}\left({\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^2\right)\mathrm{,}}\end{array}$ ami két tizedesjegyre kerekítve: $\begin{array}{c}{\displaystyle t=\frac{32}{3}\pi +2\sqrt[]{3}\approx 36\mathrm{,}97{\text{cm}}^2\mathrm{.}}\end{array}$   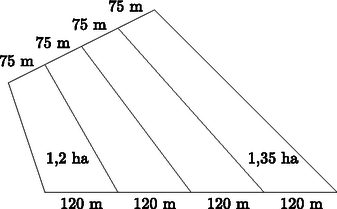9. Az ábra egy földterület rajzát adja, amelyen $4$ tulajdonos osztozik. A nyilvántartásban a középső két terület nagysága olvashatatlan. Mekkora a hiányzó két terület nagysága?        (16 pont)   Megoldás. Használjuk az 1. ábrán levő jelöléseket. 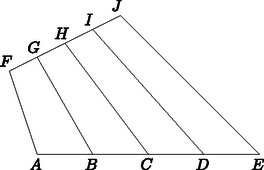  1. ábra   2. ábra Húzzunk $AE$-vel párhuzamost az $F$ ponton keresztül és bocsássunk merőlegest erre az egyenesre a másik egyenes pontjaiból (2. ábra). A párhuzamos szelőszakaszok tételét felírva: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{m_1}{FG}=\frac{m_2}{FH}=\frac{m_3}{FI}=\frac{m_4}{FJ}=\frac{m_1}{FG}=\frac{m_2}{2\cdot FG}=\frac{m_3}{3\cdot FG}=\frac{m_4}{4\cdot FG}\mathrm{,}}\hfill \\ \hfill {\displaystyle m_2=2\cdot m_1\mathrm{,}{m}_3=3\cdot m_1\mathrm{,}{m}_4=4\cdot m_1\mathrm{.}}\hfill \end{array}}$ Bocsássunk merőlegest $AE$ egyenesére a másik egyenes pontjaiból, valamint a négyszögeknek húzzuk meg az átlóit a 3. ábra szerint. Az $F$ pontból állított merőleges szakasz hosszát $x$-szel jelölve a $G$, $H$, $I$ és $J$ pontokból állított merőleges szakaszok hossza rendre $x+m_1$, $x+2m_1$, $x+3m_1$, $x+4m_1$, tehát ezek is számtani sorozatot alkotnak. Ugyanez igaz ‐ az ábrán meg nem húzott ‐ $A$, $B$, $C$, $D$, $E$ csúcsokból a másik egyenesre bocsátott merőlegesekkel. 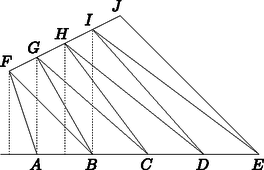    3. ábra   Az $ABGF$, $BCHG$, $CDIH$ és $DEJI$ négyszögek területét a behúzott átlók által meghatározott háromszögek területének összegeként számolva azt kapjuk, hogy a négyszögek területei is számtani sorozatot alkotnak. Tehát a területekre: $a_1=1\mathrm{,}2$ ha; $a_4=1\mathrm{,}35$ ha, ahol $\left\{a_i\right\}$ számtani sorozat. Ebből ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a_4}& {\displaystyle =a_1+3d\mathrm{,}}\hfill \\ \hfill {\displaystyle 1\mathrm{,}35}& {\displaystyle =1\mathrm{,}2+3d\mathrm{.}}\hfill \end{array}}$ Innen a differencia 0,05 ha és a hiányzó területek: 1,25 ha és 1,3 ha.   ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{<span style="font-weight: bold;">Szoldatics József</span><br> Budapest}}\hfill \end{array}}$   $*$   Helyesbítés a 2018/8. szám emelt szintű feladatsorának megoldásvázlatához. 1. Az 1.$b)$ feladat megoldásában az egyenlet jobb oldalán $-1$ áll, így a $\text{cos}x$-re kapott másodfokú egyenlet $\begin{array}{c}{\displaystyle 0=\text{cos}{}^{2}x-\text{cos}x-2=\left(\text{cos}x+1\right)\left(\text{cos}x-2\right)\mathrm{.}}\end{array}$ Mivel $\text{cos}x$ értéke nem lehet 2, így csak a $\text{cos}x=-1$ lehetséges. Ennek megoldása $x=\left(2k+1\right)\pi$ ($k\in \text{Z}$), de a megadott intervallumon ilyen nincs. Tehát az egyenletnek nincs megoldása az adott intervallumon. 2. A 8. feladat részpontszámai helyesen 5, 5, és 6. Köszönjük Németh Lászlónak, hogy a fentiekre felhívta figyelmünket.