Cím:	Megoldásvázlatok a 2018/8. sz. emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Varga Péter
Füzet:	2018/december, 526 - 536. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Oldjuk meg a valós számok halmazán az alábbi egyenletet: $\begin{array}{c}{\displaystyle \sqrt[]{x}=6-x\mathrm{.}}\end{array}$ (5 pont) $b)$ Oldjuk meg a $[-\frac{\pi }{2};0]$ intervallumon az alábbi egyenletet: $\begin{array}{c}{\displaystyle \text{sin}{}^{2}x+\text{cos}x=-1.}\end{array}$ (6 pont)   Megoldás. $a)$ I. megoldás. A négyzetgyök függvény értelmezési tartománya miatt $x\ge 0$, értékkészlete miatt $x\le 6$, ezért az egyenlet gyökei csak a $\left[0;6\right]$ halmaz elemei lehetnek. Az egyenlet mindkét oldalát négyzetre emelve és rendezve: $x^2-13x+36=0$, melynek gyökei $x_1=4$ és $x_2=9$. Utóbbi nem eleme a $\left[0;6\right]$ intervallumnak, ezért nem lehet az eredeti egyenlet gyöke. A $\left[0;6\right]$ intervallumon ekvivalens átalakításokat végeztünk, így csak $x_1=4$ gyöke az eredeti egyenletnek. 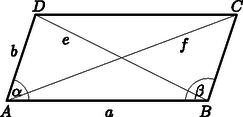II. megoldás. Tekintsük az egyenlet két oldalát, mint függvények hozzárendelési szabályát. A bal és jobb oldal függvényei: $f\left(x\right)=\sqrt[]{x}$ és $g\left(x\right)=6-x$. Ábrázoljuk a függvényeket ugyanabban a derékszögű koordináta-rendszerben. A grafikonoknak egy közös pontja van, annak első koordinátáját leolvasva: $x_1=4$. Mivel $f\left(4\right)=g\left(4\right)=2$, ezért $x_1=4$ valóban megoldás. 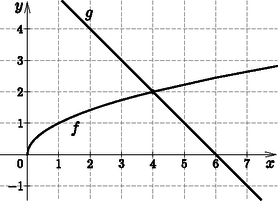    $b)$ A $\text{sin}{}^{2}x+\text{cos}{}^{2}x=1$ azonosság alapján $1-\text{cos}{}^{2}x+\text{cos}x=1$, melyet rendezve és szorzattá alakítva $\text{cos}x\left(\text{cos}x-1\right)=0$. Egy szorzat pontosan akkor 0, ha valamelyik tényezője 0, ezért az előbbi egyenlet a megadott intervallumon akkor teljesül, ha $x_1=0$ vagy $x_2=-\frac{\pi }{2}$, melyet behelyettesítéssel történő ellenőrzés, vagy ekvivalens átalakításokra történő hivatkozás igazol.   2. A májusban megírt emelt szintű matematika érettségi dolgozatok $1$. feladatának eredményessége látható az alábbi táblázatban:   ${\displaystyle \begin{array}{|cccccc|}\hline {\displaystyle \text{A vizsgált év}}\hfill & \hfill {\displaystyle \text{ 2013}}\hfill & \hfill {\displaystyle \text{ 2014}}\hfill & \hfill {\displaystyle \text{ 2015}}\hfill & \hfill {\displaystyle \text{ 2016}}\hfill & \hfill {\displaystyle \text{ 2017 }}\hfill \\ {\displaystyle \text{Eredményesség (\%)}}\hfill & \hfill {\displaystyle \text{ 84}}\hfill & \hfill {\displaystyle \text{ 88}}\hfill & \hfill {\displaystyle \text{ 79}}\hfill & \hfill {\displaystyle \text{ 86}}\hfill & \hfill {\displaystyle \text{ 83 }}\hfill \\ \hline\end{array}}$   $a)$ Határozzuk meg az eredményességek terjedelmét, átlagát és szórását.   (4 pont)   Csaba érettségi bizonyítványában az alábbi osztályzatok szerepelnek: 3; 4; 5; 4; 3; 4. $b)$ Legkevesebb hány osztályzatot kellene törölni a bizonyítványából, hogy az osztályzatok mediánja megváltozzon?  (4 pont)   Csaba $12$. osztályos év végi bizonyítványában 7 db 4-es és 5 db 5-ös osztályzat szerepel, melyek közül véletlenszerűen kiválasztunk $3$ osztályzatot.   $c)$ Igazoljuk, hogy ha az osztályzatokat visszatevés nélkül választjuk ki, akkor annak a valószínűsége, hogy 2 db 4-est és 1 db 5-öst választottunk $\frac{21}{44}$.  (4 pont)   Megoldás. $a)$ A keresett terjedelem $\left(88-79=\right)9$, az átlag $(\frac{420}{5}=)84$, a szórás pedig $\begin{array}{c}{\displaystyle \sqrt[]{\frac{0^2+4^2+5^2+2^2+1^2}{5}}=\sqrt[]{9\mathrm{,}2}\approx 3\mathrm{,}03.}\end{array}$   $b)$ Az osztályzatok mediánja 4. Ha a jegyek közül egyet törlünk ki (1 db 3-ast vagy 1 db 4-est vagy 1 db 5-öst), akkor a medián ugyanúgy 4 marad. Ha a jegyek közül kettőt törlünk ki, akkor a medián csak úgy változhat meg, ha a két középső osztályzat átlaga nem 4 lesz, ami 2 esetben is teljesül (3; 3; 4; 5 vagy 3; 3; 4; 4). Ezért legkevesebb 2 osztályzatot kell kitörölni, hogy a medián megváltozzon.   $c)$ A 12 osztályzat közül hármat $\left(\genfrac{}{}{0ex}{}{12}{3}\right)\left(=220\right)$-féleképpen választhatunk ki. Ez az összes eset száma. A 7 db 4-esből 2-őt és az 5 db 5-ösből 1-et $\left(\genfrac{}{}{0ex}{}{7}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{5}{1}\right)\left(=105\right)$-féleképpen választhatunk ki. Ez a kedvező esetek száma. A keresett valószínűség: $\begin{array}{c}{\displaystyle \frac{\left(\genfrac{}{}{0ex}{}{7}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{5}{1}\right)}{\left(\genfrac{}{}{0ex}{}{12}{3}\right)}=\frac{21}{44}\mathrm{.}}\end{array}$   3. Egy paralelogrammában az átlóhosszak négyzetének összege 74,45, az átlóhosszak négyzetének különbsége 32,13. $a)$ Számítsuk ki a paralelogramma átlóinak hosszát.  (4 pont) $b)$ Igaz-e, hogy a paralelogramma átlóinak felezőpontján átmenő, annak hosszabbik oldalával párhuzamos egyenes két egyenlő területű részre osztja a paralelogrammát?  (4 pont) $c)$ Határozzuk meg a paralelogramma szomszédos oldalhosszainak négyzetösszegét.  (6 pont)   Megoldás. $a)$ I. megoldás. Jelölje a paralelogramma átlóit $e$ és $f$, ekkor a feladat szövege alapján megoldandó az alábbi egyenletrendszer: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle e^2+f^2}& {\displaystyle =74\mathrm{,}\mathrm{45,}}\hfill \\ \hfill {\displaystyle e^2-f^2}& {\displaystyle =32\mathrm{,}13.}\hfill \end{array}}\}}\end{array}$ A két egyenletet összeadva: $2e^2=106\mathrm{,}58$. Ebből $e=7\mathrm{,}3$, majd $f=4\mathrm{,}6$. II. megoldás. Jelölje a paralelogramma átlóit $e$ és $f$, ekkor a feladat szövege alapján megoldandó az alábbi egyenletrendszer: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle e^2+f^2}& {\displaystyle =74\mathrm{,}\mathrm{45,}}\hfill \\ \hfill {\displaystyle e^2-f^2}& {\displaystyle =32\mathrm{,}13.}\hfill \end{array}}\}}\end{array}$ Az első egyenletből $f^2=74\mathrm{,}45-e^2$, ezt a második egyenletbe helyettesítve: $2e^2=106\mathrm{,}58$. Ebből $e=7\mathrm{,}3$, majd $f=4\mathrm{,}6$. $b)$ A paralelogramma átlói felezik egymást, ezért a $BDT$ háromszög a $BMQ$ háromszögnek $B$ középpontú, 2-szeres nagyítású képe. Ezért az $ABFE$ paralelogramma magassága ugyanakkora, mint az $EFCD$ paralelogramma magassága. Mivel $AB=EF$, így igaz, hogy $T_{ABEF}=T_{EFCD}$.   b)   c) $c)$ Az ábra jelöléseit használva írjuk fel az $ABD$ és $ABC$ háromszögekre a koszinusztételt: az $ABD$ háromszögben: $e^2=a^2+b^2-2ab\text{cos}\alpha$, az $ABC$ háromszögben: $f^2=a^2+b^2-2ab\text{cos}\beta$. Mivel $ABCD$ paralelogramma, ezért $\text{cos}\beta =\text{cos}\left({180}^{\circ }-\alpha \right)=-\text{cos}\alpha$. Ezért $f^2=a^2+b^2+2ab\text{cos}\alpha$. Így $e^2+f^2=2a^2+2b^2$, ahonnan $a^2+b^2=\frac{e^2+f^2}{2}=37\mathrm{,}225$.   4. Egy konyhai papírtörlő tekercs $80$ darab 0,5 mm vastag téglalap alakú lapból áll. Egy papírlap 240 mm hosszú és 230 mm széles téglalap, melyek a szélességüknél perforációs (tépést megkönnyítő) résszel kapcsolódnak egymáshoz. A tekercs közepén lévő üres henger átmérője 40 mm. $a)$ Hány teljes fordulatot tesz meg az üres henger, ha az egész papírtekercset körbe letekerjük? (A perforációs részek méretétől tekintsünk el.)  (9 pont)     Az egyik ismert márkájú papírtörlő tekercs lapjaira mintákat is nyomtatnak. A gyártósoron $8$ különböző mintából csak $3$-féle mintát használnak fel egy lapra. A gyártósoron az összes lehetséges mintahármast beállítják a gépeken, amelyeket egymás után folyamatosan nyomtatnak a papírtörlő lapjaira. $b)$ Mekkora annak a valószínűsége, hogy egy adott tekercs egy lapját kiválasztva a tekercsen van még egy ugyanilyen mintázatú másik lap?  (5 pont)   Megoldás. $a)$ A 80 téglalap alakú papírlap összesen $80\cdot 240=19200\text{ mm}=19\mathrm{,}2$ m hosszú. Az első réteg hossza az üres hengeren $2\cdot 20\cdot \pi \left(\approx 125\mathrm{,}66\right)$ mm. A második réteg hossza az üres hengeren: $2\cdot 20\mathrm{,}5\cdot \pi \left(\approx 128\mathrm{,}81\right)$ mm. Észrevehető, hogy az egyes rétegek hosszának összege az üres hengeren: $\begin{array}{c}{\displaystyle 2\pi [20+20\mathrm{,}5+21+\text{...}+\left(20+\left(n-1\right)\cdot 0\mathrm{,}5\right)]\mathrm{,}}\end{array}$ ahol $n$ a teljes fordulatok száma. A szögletes zárójelben egy számtani sorozat első $n$ tagjának összege van ($a_1=20$, $d=0\mathrm{,}5$). $\begin{array}{c}{\displaystyle S_n=\frac{40+\left(n-1\right)\cdot 0\mathrm{,}5}{2}\cdot n=0\mathrm{,}25n^2+19\mathrm{,}75n\mathrm{,}}\end{array}$ így megoldandó a $0\mathrm{,}5\pi \cdot n^2+39\mathrm{,}5\pi \cdot n-19200=0$ egyenlet. Az egyenlet gyökei $n_1\approx 77\mathrm{,}9$ és $n_2\approx -156\mathrm{,}9$, melyek közül utóbbi nyilván nem lehet a feladat megoldása. Tehát az üres henger 77 teljes fordulatot tesz meg, ha az egész papírtekercset körbe letekerjük. $b)$ A gyártósoron $\left(\genfrac{}{}{0ex}{}{8}{3}\right)\left(=56\right)$-féle különböző mintát használnak fel, ez az összes eset száma. A 80 lapból álló papírtörlő tekercsen $\left(80-56=\right)24$ minta két papírlapon is szerepel, így a kedvező esetek száma 48. Az ismétlődés független attól, hogy egy adott tekercsen melyik mintával kezd a gép. Tehát a keresett valószínűség $\frac{48}{80}=0\mathrm{,}6$.   II. rész     5. A térképrészleten egy háromszög alakú telek látható, melynek Toldi úti oldala 50 m, Petőfi úti oldala 65 m és Mikszáth úti oldala 75 m hosszú. A telket Csaba, László és Levente örökli, akik megállapodnak, hogy a Toldi úttal párhuzamos kerítésekkel három egyenlő területű részre osztják fel a telket úgy, hogy mindenkinek legyen kijárata a Mikszáth útra, a főútra. $a)$ Milyen hosszú drótkerítést kell venniük a telkek szétválasztásához?  (6 pont) 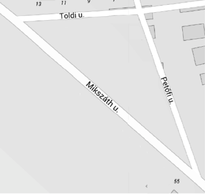    A helyi építési szabályzat nem engedélyezi olyan épület építését, amelynek két szomszédos fala által bezárt szög ${60}^{\circ }$-nál kisebb. $b)$ Kiadható-e építési engedély arra az épületre, amelyet úgy terveznek, hogy a Toldi és a Mikszáth utca sarkán fog állni, és külső falai ezzel a két utcával párhuzamosak lesznek?  (4 pont) Csaba, László és Levente megállapodtak abban, hogy a telek felosztása után kockadobással döntik el, hogy milyen sorrendben választanak a telkek közül. Mindenki dob egyet egy szabályos dobókockával, és ha nincs azonos dobás, akkor a legnagyobbat dobó választ először, majd a második legnagyobbat dobó másodszor, végül a legkisebb számot dobó kapja a maradék telekrészt. Ha van egyenlő a dobott számok között, akkor a dobás érvénytelen és addig dobnak újra, amíg nem lesz három különböző eredmény. $c)$ Mekkora valószínűséggel választ először Levente telket?  (6 pont)   Megoldás. $a)$ Tekintsük a feladat szövege alapján az ábrát. Mivel a fiúk egyenlő területű részekre osztják a telket, ezért 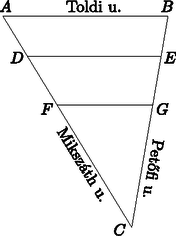$T_{ABED}=T_{DEGF}=T_{FGC}=\frac{1}{3}{T}_{ABC}$. Az $AB$ oldallal párhuzamos felosztás és a megfelelő szögek páronkénti egyenlősége miatt az $ABC▵\sim FGC▵$, így a hasonló síkidomok területének arányára vonatkozó tétel miatt $\begin{array}{c}{\displaystyle FG=\sqrt[]{\frac{1}{3}}\cdot AB\left(\approx 28\mathrm{,}9\text{ m}\right)\mathrm{.}}\end{array}$     Hasonlóan az $AB$ oldallal párhuzamos felosztás és a megfelelő szögek páronkénti egyenlősége miatt az $ABC▵\sim DEC▵$, így a hasonló síkidomok területének arányára vonatkozó tétel miatt $\begin{array}{c}{\displaystyle DE=\sqrt[]{\frac{2}{3}}\cdot AB\left(\approx 40\mathrm{,}8\text{ m}\right)\mathrm{.}}\end{array}$ A telkek szétválasztásához a fiúknak kb. 69,7 m hosszú drótkerítést kell venniük. $b)$ Akkor nem adható ki építési engedély az építendő épületre, ha az $ABC$ háromszög $A$ csúcsánál lévő $\alpha$ szöge ${60}^{\circ }$-nál kisebb. Az $\alpha$ szög meghatározásához az $ABC$ háromszögben a koszinusztételt alkalmazva: $\begin{array}{c}{\displaystyle {65}^2={50}^2+{75}^2-2\cdot 50\cdot 75\cdot \text{cos}\alpha \mathrm{,}\text{ahonnan}\text{cos}\alpha =\frac{13}{25}\mathrm{.}}\end{array}$ Mivel $\begin{array}{c}{\displaystyle \text{cos}{60}^{\circ }=\frac{1}{2}<\text{cos}\alpha =\frac{13}{25}\mathrm{,}}\end{array}$ ezért $\alpha <{60}^{\circ }$, tehát az építési engedély nem adható ki. $c)$ A keresett valószínűség a kedvező esetek számának és az összes eset számának hányadosaként számítható ki. Az összes esetet azok a dobások alkotják, amikor mindhárom dobás különböző. Ezek száma $6\cdot 5\cdot 4=120$. Vizsgáljuk a kedvező esetek számát Levente dobása szerint: Ha Levente 1-est vagy 2-est dob, akkor a kedvező esetek száma 0. Ha Levente 3-ast dob, akkor a kedvező esetek száma $2\cdot 1=2$. Ha Levente 4-est dob, akkor a kedvező esetek száma $3\cdot 2=6$. Ha Levente 5-öst dob, akkor a kedvező esetek száma $4\cdot 3=12$. Ha Levente 6-ost dob, akkor a kedvező esetek száma $5\cdot 4=20$. Így a kedvező esetek száma 40. Ezért a keresett valószínűség: $\frac{40}{120}=\frac{1}{3}$.   6. Adott a valós számok halmazán értelmezett $f$ és $g$ függvény: $\begin{array}{c}{\displaystyle f\left(x\right)=\frac{x^3}{8}-\frac{x^2}{2}+\frac{x}{2}\text{és}g\left(x\right)=-x^2+2x\mathrm{.}}\end{array}$ $a)$ Adjuk meg az $f$ függvény lokális szélsőértékhelyeit.  (5 pont) $b)$ Igazoljuk, hogy az $f$ és $g$ függvények grafikonjának három közös pontja van.   (5 pont) $c)$ Számítsuk ki az $f$ és $g$ függvények grafikonja által közbezárt terület nagyságát az $x_1=0$ és $x_2=2$ határok között.  (6 pont)   Megoldás. $a)$ Az $f$ függvénynek csak ott lehet lokális szélsőértéke, ahol $f\text{'}$-nek zérushelye van. $\begin{array}{c}{\displaystyle f\text{'}\left(x\right)=\frac{3}{8}{x}^2-x+\frac{1}{2}\mathrm{,}}\end{array}$ így megoldandó a $\begin{array}{c}{\displaystyle \frac{3}{8}{x}^2-x+\frac{1}{2}=0}\end{array}$ egyenlet. A deriváltfüggvény zérushelyei: $x_1=\frac{2}{3}$ és $x_2=2$. Mivel a deriváltfüggvény $x<\frac{2}{3}$ és $x>2$ esetén pozitív, $\frac{2}{3}<x<2$ esetén pedig negatív, ezért az $f$ függvénynek $x_1=\frac{2}{3}$-ban lokális maximumhelye, $x_2=2$-ben pedig lokális minimumhelye van. $b)$ A metszéspontok meghatározásához megoldandó az $\begin{array}{c}{\displaystyle \frac{x^3}{8}-\frac{x^2}{2}+\frac{x}{2}=-x^2+2x}\end{array}$ egyenlet. Az előbbi egyenletrendezés és szorzattá alakítás után: $x\left(x^2+4x-12\right)=0$. Egy szorzat pontosan akkor 0, ha valamelyik tényezője 0, ezért az egyenlet gyökei: $x_1=0$; $x_2=-6$ és $x_3=2$. Tehát az $f$ és $g$ függvények grafikonjának valóban három közös pontja van. $c)$ Mivel a felvett függvényértékek a megadott határok között pozitívak és a $g$ függvény grafikonja az $f$ függvény grafikonja fölött helyezkedik el, ezért a keresett $T$ területre fennáll: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T}& {\displaystyle =\underset{0}{\overset{2}{\int }}\left[\left(-x^2+2x\right)-\left(\frac{x^3}{8}-\frac{x^2}{2}+\frac{x}{2}\right)\right]\text{d}x=\underset{0}{\overset{2}{\int }}\left(-\frac{x^3}{8}-\frac{x^2}{2}+\frac{3x}{2}\right)\text{d}x=}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={\left[-\frac{x^4}{32}-\frac{x^3}{6}+\frac{3x^2}{4}\right]}_0^2=\left(-\frac{2^4}{32}-\frac{2^3}{6}+\frac{3\cdot 2^2}{4}\right)=\frac{7}{6}\mathrm{.}}\hfill \end{array}}$   7. $a)$ Hány különböző $124$ jegyű tízes számrendszerbeli természetes szám képezhető 62 db nulla és 62 db egyes számjegyből? (Elegendő csak a kiszámítás módját megadni.)  (3 pont) $b)$ Mutassuk meg, hogy a 62 db nullából és 62 db egyesből álló $124$-jegyű tízes számrendszerbeli természetes számok egyike sem lehet négyzetszám.  (5 pont) $c)$ Határozzuk meg annak a számrendszernek az alapszámát, amelyben a $124$ felírható olyan $3$ jegyű számként, melynek minden számjegye azonos.  (8 pont)   Megoldás. $a)$ Mivel a képzett szám 124 jegyű, ezért első jegye csak 1-es lehet. Annyi ilyen szám képezhető, ahányféleképpen a maradék 62 db nullát és 61 db 1-est sorba lehet rendezni. A keresett sorrendek (és egyben képezhető számok) száma: $\frac{123!}{62!\cdot 61!}$. $b)$ Egy természetes szám 3-mal osztva 0, 1 vagy 2 maradékot adhat. 3-mal osztható szám négyzete biztosan osztható 3-mal, mert ${\left(3k\right)}^2=9k^2$. 3-mal osztva 1 maradékot adó szám négyzete 3-mal osztva biztosan 1 maradékot ad, mert ${\left(3k+1\right)}^2=9k^2+6k+1$. 3-mal osztva 2 maradékot adó szám négyzete 3-mal osztva biztosan 1 maradékot ad, mert $\begin{array}{c}{\displaystyle {\left(3k+2\right)}^2=9k^2+12k+4=3\cdot \left(3k^2+4k+1\right)+1.}\end{array}$ Mivel bármely képzett számban a számjegyek összege 62, mely 3-mal osztva 2 maradékot ad, ezért biztos, hogy a képzett szám nem lehet négyzetszám. $c)$ Jelölje a keresett számrendszer alapszámát $x$, a szám alakját ebben a számrendszerben $\overline{AAA}$. Az $\overline{AAA}$ alaki értékű szám valódi értéke az $x$ alapú számrendszerben: $A{x}^2+Ax+A=A\left(x^2+x+1\right)$, tehát a szám osztható $A$-val. A 124 prímtényezős felbontása $2^2\cdot 31$, így az $A$ szám lehetséges értékei 124 pozitív osztói: 1; 2; 4; 31; 62; 124. Mivel egy számrendszer alapszáma legalább 2, $x^2+x+1\ge 7$, ezért $A$ legfeljebb $[\frac{124}{7}]=17$ lehet. Ha $A=1$, akkor az $x^2+x+1=124$ másodfokú egyenletnek nincs egész megoldása. Ha $A=2$, akkor az $x^2+x+1=62$ másodfokú egyenletnek nincs egész megoldása. Ha $A=4$, akkor az $x^2+x+1=31$ másodfokú egyenlet megoldásai: $x_1=-6$ és $x_2=5$. Negatív szám nem lehet a számrendszer alapszáma, ezért a keresett alapszám 5. Ebben a számrendszerben valóban létezik a ${444}_5$ szám.   8. Az egyetemi felvételi eljárásban július közepéig lehet módosítani azoknak a szakoknak a sorrendjét, amelyekre felvételizni szeretnénk. Márta $5$ különböző államilag támogatott képzésre jelentkezett, és közülük három szak esetén beadta a jelentkezést az önköltséges képzésre is. $a)$ Hány különböző sorrendben adhatja be a módosításnál ezeket a szakokat, ha az nem fordulhat elő, hogy egy bizonyos szakból előkelőbb helyen áll az önköltséges képzés, mint az államilag finanszírozott?  (5 pont) Márta a módosítás után sajnos csak az önköltséges képzésre jutott be, amelynek díja félévenként 250 000 Ft. Szülei az elmúlt $5$ évben havi 20 000 Ft-ot tettek félre erre a célra. A megtakarítás $5$ évig egy olyan számlán volt, amely havonta $1\%$-ot kamatozott, és az összeget havonta tőkésítették. $b)$ Legfeljebb hány félévnyi tandíjra elegendő a teljes lekötött összeg?  (5 pont) Márta úgy döntött, hogy a lekötött összegből 500 000 Ft-ot rögtön berak a bankba, majd a következő év elején még újabb 500 000 Ft-ot hozzátesz. Ebben a konstrukcióban a kamatot évente tőkésítették, azaz minden év végén adták hozzá a bent lévő összeghez a kamatot. $c)$ Hány százalék volt az éves kamat, ha Márta a második év végén csak a kamatokból 76 250 Ft-ot tudott felvenni?  (7 pont)   Megoldás. $a)$ Jelölje a különböző államilag támogatott képzéseket $A$, $B$, $C$, $D$, $E$, és a megfelelő önköltséges képzéseket $a$, $b$, $c$. A beadott 8Íkülönböző szaknak összesen $8!\left(=40320\right)$-féle sorrendje lehet. Minden olyan lehetséges sorrendhez, amelyben $A$ megelőzi $a$-t (a szimmetria miatt) pontosan egy olyan sorrend tartozik, amely csak annyiban különbözik, hogy $A$-t és $a$-t felcseréljük, ezért a lehetséges sorrendek számát osztanunk kell 2-vel. Hasonlóan osztanunk kell 2-vel $B$ és $b$, valamint $C$ és $c$ sorrendjei miatt is, ezért a keresett sorrendek száma $\frac{8!}{2^3}-1\left(=7!-1\right)=5039$. $b)$ A bankba havonta betett összegek egy 1,01 hányadosú mértani sorozat egymást követő tagjai, ahol a sorozat első tagja $\left(20000\cdot 1\mathrm{,}01=\right)20200$. Az 5 év alatt összegyűjtött összeg a mértani sorozat első 60 tagjának összege, ezért ezt az összeget kell kiszámolni. A mértani sorozat összegképletébe behelyettesítve: $\begin{array}{c}{\displaystyle S_{60}=20200\cdot \frac{1\mathrm{,}{01}^{60}-1}{1\mathrm{,}01-1}\approx 1649727\text{(Ft).}}\end{array}$ Ez az összeg 6 félévre elegendő. $c)$ Jelölje a befizetett összeg éves növekedését $p$. Ekkor az első év elején befizetett összeg $p^2$-szeresére, a második év végén befizetett összeg $p$-szeresére nő. Ezért megoldandó az $500000\cdot x^2+500000\cdot x=1076250$ egyenlet. Az egyenletet rendezve és egyszerűsítve: $\begin{array}{c}{\displaystyle 400\cdot x^2+400\cdot x-861=0.}\end{array}$ Az előbbi másodfokú egyenlet megoldásai: $x_1=1\mathrm{,}05$ és $x_2=-2\mathrm{,}05$, melyek közül utóbbi nyilván nem lehet a feladat megoldása. Tehát az éves kamat 5% volt.   9. Az Oroszországban rendezett labdarúgó világbajnokságra nagy létszámú horvát baráti társaság utazott ki. Az első három horvát mérkőzést a társaság 90-90-90%-a tekintette meg. $a)$ Legalább, illetve legfeljebb a szurkolók hány százaléka láthatta mindhárom mérkőzést?  (4 pont) Horvátország az első mérkőzését Nigéria ellen vívta a kalinyingrádi (régi porosz Königsberg) stadionban. Egy sorban $12$ horvát szurkoló ült, akik közül néhányan kézfogással köszöntötték egymást. $b)$ Lehetséges-e, hogy az egyes szurkolók 11, 10, 11, 6, 9, 11, 7, 4, 8, 11, 5, 11 másik szurkolóval fogtak kezet?  (3 pont) Egy szabadrúgás alkalmával az $L$ pontban lévő labda éppen 16,5 m-re van az alapvonaltól. Az alapvonalnak a labdához legközelebb levő $V$ pontja ugyancsak 16,5 m-re van az alapvonalon elhelyezkedő 7,32 m széles és 2,44 m magas kapu labdához közelebbi függőleges kapufájának $B$ talppontjától. 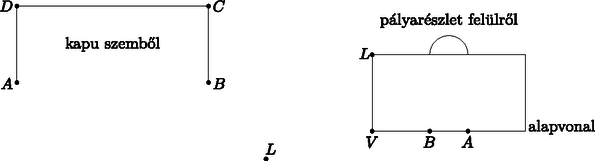    $c)$ Mekkora szögben látja a $L$ pontban álló focista a $BD$ szakaszt, ha szemmagassága 174 cm-en van?  (9 pont)   Megoldás. $a)$ Ha a ,,legalább mennyien láthatták mindhárom mérkőzést'' kérdésre szeretnénk választ kapni, akkor a lehető legtöbb szurkolót kell kijuttatni a mérkőzésekre. A három mérkőzésre $3\cdot 0\mathrm{,}9=2\mathrm{,}7$, azaz a társaság létszámának 270%-ának megfelelő mennyiségű jegy kelt el. Látható, hogy a 270%-nyi jegymennyiség 2 mérkőzés megtekintését mindenki számára lehetővé teszi, a maradék pedig biztosítja, hogy a csoport legalább 70%-a látja mindhárom mérkőzést. A társaság legfeljebb 90%-a látja mindhárom mérkőzést, ha 10%-uk egyáltalán nem megy ki arra. $b)$ A kézfogások számából látható, hogy 5 szurkoló 11 másikkal fogott kezet, azaz öten mindenkivel kezet fogtak. Az előbbi megállapítás miatt biztosan nem lehet olyan szurkoló, akinek 5-nél kevesebb kézfogása volt. Mivel az adatok szerint van olyan szurkoló, aki 4 társával fogott kezet, ezért a kézfogások száma így nem lehetséges. $c)$ Jelölje az $L$ pontban álló   focista szemmagasságát $S$. Így a $DSB\sphericalangle =\alpha$ szöget kell meghatározni. A kapu $BD$ átlójának hossza a Pitagorasz-tétellel: 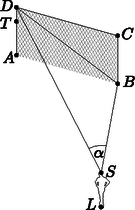$\begin{array}{c}{\displaystyle BD=\sqrt[]{7\mathrm{,}{32}^2+2\mathrm{,}{44}^2}\approx 7\mathrm{,}72\text{m}\mathrm{.}}\end{array}$ $SB$ meghatározásához szükségünk van $LB$ távolságára. A Pitagorasz-tételt az $LVB$ majd az $LSB$ háromszögekre alkalmazva: $\begin{array}{c}{\displaystyle SB=\sqrt[]{16\mathrm{,}{5}^2+16\mathrm{,}{5}^2+1\mathrm{,}{74}^2}\approx 23\mathrm{,}4\text{m}\mathrm{.}}\end{array}$     $SD$ meghatározásához az $AD$ szakasz ,,szemmagasságú'' pontja legyen $T$. Ekkor $TD=2\mathrm{,}44-1\mathrm{,}74=0\mathrm{,}7$ m lesz. Felhasználva, hogy az $AVL$ és $STD$ háromszögek is derékszögűek, valamint $ST=LA=\sqrt[]{16\mathrm{,}{5}^2+{\left(16\mathrm{,}5+7\mathrm{,}32\right)}^2}$, az $SD$ szakasz hosszára $SD=\sqrt[]{16\mathrm{,}{5}^2+{\left(16\mathrm{,}5+7\mathrm{,}32\right)}^2+0\mathrm{,}{7}^2}\approx 28\mathrm{,}99$ m adódik. Az oldalhosszak ismeretében a $BDS$ háromszögre a koszinusz-tételt alkalmazva: $\begin{array}{c}{\displaystyle B{D}^2=B{S}^2+S{D}^2-2\cdot BS\cdot SD\cdot \text{cos}\alpha \mathrm{.}}\end{array}$ $\text{cos}\alpha \approx 0\mathrm{,}9791$, ahonnan $\alpha \approx 11\mathrm{,}{7}^{\circ }$. Tehát a keresett látószög kb. $11\mathrm{,}{7}^{\circ }$.