Cím:	Politópok és a gömb d-dimenzióban
Szerző(k):	Naszódi Márton
Füzet:	2018/december, 516 - 524. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Politópok és a gömb $d$-dimenzióban   Gauss tizenkilenc éves korában igazolta, hogy a szabályos 17-szög (magyarul heptadekagon) megszerkeszthető körző és vonalzó használatával [1]. Eredményére annyira büszke volt, hogy úgy rendelkezett, hogy a sírkövére véssenek egy szabályos 17-szöget. A sírkőfaragók erre nem voltak hajlandók, mert a szabályos 17-szög lényegében egy kör. Ebben a cikkben nem Gauss munkájával foglalkozunk, hanem a sírkőfaragók fenti igazságával.   1. ábra. Szabályos 17-szög   A modern sírkőfaragók már nemcsak síkbeli ábrákkal dolgoznak, hanem térbeliekkel is, ők a szobrászok és a hologram-készítők. És az igazán modern sírkőfaragók magasabb dimenziós ábrákkal is dolgoznak, ők a matematikusok, sőt, mára már a fizikusok, közgazdászok, és a biológusok is. Azt fogjuk körüljárni, mennyire lehet egy $d$-dimenziós konvex testet egy politóppal (a sokszög magasdimenziós megfelelője) közelíteni. Ehhez persze tisztázni kell, hogy mi az a $d$-dimenziós konvex test, mi az, hogy politóp, és mit jelent az, hogy egy politóp közel van egy konvex testhez.   1. Ha a négy dimenzió a téridő, akkor a hat dimenzió az a ,,téridőhőmérsékletpáratartalom''? Lényegében igen. Kicsit pontosabban: megtanultuk, hogy a síkban, miután felvettünk egy koordinátarendszert, a pontok helyett beszélhetünk valós számpárokról, $\left(x;y\right)$. A koordináták nyelvén nem csak pontokról, hanem ponthalmazokról is tudunk beszélni. Felírhatjuk például a $\left(2;7\right)$ középpontú, 3 sugarú kör egyenletét: ${\left(x-2\right)}^2+{\left(y-7\right)}^2=9$, vagy egy egyenes egyenletét: $15x-3y+8=0$. Innen kis lépés a tér pontjait valós számokból álló hármasokkal, $\left(x;y;z\right)$ azonosítani. Aztán felírhatjuk bizonyos térbeli alakzatok egyenleteit is. Például a $\left(2;7;-8\right)$ középpontú, 3 sugarú gömbhéj egyenlete ${\left(x-2\right)}^2+{\left(y-7\right)}^2+{\left(z+8\right)}^2=9$, vagy egy sík egyenlete $15x-3y+15z+8=0$. Most egy nagyon bátor lépés következik: írjunk egy zárójelen belülre 6 számot egymástól pontosvesszővel gondosan elválasztva: $\left(x_1;x_2;x_3;x_4;x_5;x_6\right)$. Így például $\left(-2;-3;\mathrm{22,5};9;11;8\right)$ egy pont a hatdimenziós térben, amelyet ‐ mivel valós számhatosok alkotják ‐ ${\text{R}}^6$-tal jelölünk (és mondjuk ,,err ad hat''-nak olvashatunk).   De mi ennek az értelme? Amit hat valós számmal lehet leírni, arról beszélhetek úgy, mint ${\text{R}}^6$ egy pontjáról. Ha mondjuk megmérjük egy hangya 6 lábának a hosszát, akkor kapunk egy pontot $\left(x_1;x_2;\text{...};x_6\right)\in {\text{R}}^6$. Egy másik hangya ad egy másik pontot $\left(x_1\text{'};x_2\text{'};\text{...};x_6\text{'}\right)\in {\text{R}}^6$. Hogyan fejezzük ki azt, hogy a két hangya mennyire hasonló? Vegyük a két ${\text{R}}^6$-beli pont távolságát, amelyet, a két- és háromdimenziós eset kiterjesztéseként definiálhatunk így: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle d\left(\left(x_1;x_2;\text{...};x_6\right)\mathrm{,}\left(x_1\text{'};x_2\text{'};\text{...};x_6\text{'}\right)\right):=}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle :=\sqrt[]{{\left(x_1-x_1\text{'}\right)}^2+{\left(x_2-x_2\text{'}\right)}^2+\text{...}+{\left(x_6-x_6\text{'}\right)}^2}\mathrm{.}}\hfill \end{array}}$ Hogyan lehet elképzelni a hatdimenziós teret? Erre nincs kanonikus válasz, én úgy képzelem el, mint a háromdimenziósat, persze tudva, hogy ez a kép valamennyire pontatlan. Például az $5x_1-3x_2+8x_3-12x_4+2x_5+3x_6+8=0$ egyenlet egy hipersíkot ír le, amelyet ugyanúgy lehet elképzelni, mint egy síkot a térben. És ez a kép jó is, például éppen úgy két féltérre osztja ${\text{R}}^6$-ot, ahogyan egy sík is ${\text{R}}^3$-at: vannak olyan pontok ${\text{R}}^6$-ban, melyekre $5x_1-3x_2+8x_3-12x_4+2x_5+3x_6+8\ge 0$, és vannak olyanok, melyekre $5x_1-3x_2+8x_3-12x_4+2x_5+3x_6+8\le 0$. De vigyázni kell ezzel a képpel, mert míg két általános helyzetű sík metszete egy egyenes, háromé pedig egy pont ${\text{R}}^3$-ban, addig ${\text{R}}^6$-ban két általános helyzetű hipersík metszete egy $4$-dimenziós ponthalmaz, három általános helyzetű hipersík metszete pedig egy $3$-dimenziós ponthalmaz ${\text{R}}^6$-ban (most a dimenziót és az általános helyzetet nem definiálom).   2. ${\text{R}}^d$ geometriája Legyen mostantól $d$ egy pozitív egész szám. Az eddigiek alapján a $d$ koordinátából álló pontok terét ${\text{R}}^d$-vel jelöljük, és elemeit hol vektoroknak, hol pontoknak hívjuk. Megvan tehát a terünk ponthalmaza, kell még néhány mennyiség, struktúra, amelyektől ennek a térnek geometriája is lesz. Erről szól ez a fejezet.   2.1. Távolság, szög. A távolság és a szög definíciójához is a skaláris szorzáson keresztül jutunk majd el, ez a központi fogalom. Két $d$-dimenziós vektornak, $\text{u}=\left(u_1;u_2;\text{...};u_d\right)$-nak, illetve $\text{v}=\left(v_1;v_2;\text{...};v_d\right)$-nek a skaláris szorzatát az $\begin{array}{c}{\displaystyle \langle \text{u}\mathrm{,}\text{v}\rangle :=u_1{v}_1+u_2{v}_2+\text{...}+u_d{v}_d}\end{array}$ (2) képlettel definiáljuk. Ennek segítségével definiálhatjuk egy vektor hosszát, $|\text{v}|:=\sqrt[]{\langle \text{v}\mathrm{,}\text{v}\rangle }$. Vegyük észre, hogy ez éppen a két- és háromdimenziós definíció általánosítása: a koordináták négyzetösszegének gyöke. Ebből kapjuk két pont távolságát, $d\left(\text{u}\mathrm{,}\text{v}\right):=|\text{u}-\text{v}|$, ami persze éppen az (1) egyenlet átírva $d$ koordinátára. Így már tudjuk, mi az origó középpontú $\rho >0$ sugarú (tömör) gömb: azon $\left(x_1;x_2;\text{...};x_d\right)\in {\text{R}}^d$ pontok halmaza, melyekre teljesül az $x_1^2+x_2^2+\text{...}+x_d^2\le {\rho }^2$ egyenlőtlenség. Ezt $\text{B}\left(\rho \right)$-val fogjuk jelölni, és ha $\rho =1$, akkor elhagyjuk, és egyszerűen $\text{B}$-t írunk. Azt is meg tudjuk fogalmazni, hogy egy alakzat ,,nem nyúlik a végtelenbe'': a $H\subseteq {\text{R}}^d$ halmazt korlátosnak hívjuk, ha van olyan $\rho >0$ valós szám, amelyre $H$ benne van $\text{B}\left(\rho \right)$-ban.   A skaláris szorzatot középiskolában a sík, illetve a tér két, $\alpha$ szöget bezáró vektorára az $\langle \text{u}\mathrm{,}\text{v}\rangle :=|\text{u}||\text{v}|\text{cos}\alpha$ képlettel szoktuk definiálni, aztán belátjuk a (2) képletet. Most (2) a definíció, és belátható (ezt nem tesszük meg), hogy a síkon, illetve a térben igaz a koszinuszos képlet. A szöget $d$-dimenzióban egyszerűen a skaláris szorzásból definiáljuk, amit egy kicsit elő kell készíteni.   A Cauchy‐Bunyakovszkij‐Schwarz-egyenlőtlenség szerint bármely $u_1\mathrm{,}\text{...}\mathrm{,}{u}_d$ és $v_1\mathrm{,}\text{...}\mathrm{,}{v}_d$ valós számokra teljesül, hogy $\begin{array}{c}{\displaystyle |\sum _{i=1}^d{u}_i{v}_i|\le |\sum _{i=1}^d{u}_i^2{|}^{1/2}|\sum _{i=1}^d{v}_i^2{|}^{1/2}\mathrm{,}}\end{array}$ (ezt most nem bizonyítjuk), ami másképp így írható: $|\langle \text{u}\mathrm{,}\text{v}\rangle |\le |\text{u}||\text{v}|$. Definiáljuk ezért az $\text{u}$ és $\text{v}$ vektorok szögét úgy, mint az az $\alpha \in \left[\mathrm{0,}\pi \right]$ valós szám, melyre $\begin{array}{c}{\displaystyle \text{cos}\alpha =\frac{\langle \text{u}\mathrm{,}\text{v}\rangle }{|\text{u}||\text{u}|}\mathrm{.}}\end{array}$ Feladat: Lássuk be, hogy a távolságra teljesül a háromszög-egyenlőtlenség, azaz tetszőleges három $\text{u}\mathrm{,}\text{v}\mathrm{,}\text{z}\in {\text{R}}^d$ pontra igaz, hogy $d\left(\text{u}\mathrm{,}\text{v}\right)+d\left(\text{v}\mathrm{,}\text{z}\right)\ge d\left(\text{u}\mathrm{,}\text{z}\right)$. Ez az állítás és sok hasonló több-kevesebb számolást igényel, azonban mind hihetőbbé válnak, ha magunkévá tesszük azt a geometriai képet, hogy bármely 3 pont egy (kétdimenziós) síkban van, és az ${\text{R}}^d$-beli távolság ebben a síkban pontosan a sík szokásos geometriáját adja meg.   2.2. Konvex halmazok. Ahhoz, hogy konvex halmazokról beszélhessünk, tudnunk kell, mi az a szakasz. Adott két vektor, $\text{u}\mathrm{,}\text{v}\in {\text{R}}^d$. Hogy kapjuk meg a szakaszuk felezőpontját? Az $\frac{1}{2}\text{u}+\frac{1}{2}\text{v}$ képlettel. És az $\text{u}$-hoz közelebbi harmadolópontját? A $\frac{2}{3}\text{u}+\frac{1}{3}\text{v}$ képlettel (ezt gondoljuk végig a síkon vagy a térben). Így nem meglepő, hogy általában a szakasz tetszőleges pontját ${\lambda }_1\text{u}+{\lambda }_2\text{v}$ alakban kapjuk meg, ahol ${\lambda }_1\mathrm{,}{\lambda }_2$ nemnegatív valós számok, melyek összege 1. A szakaszra egy jelölést is bevezetünk: $\left[\text{u}\mathrm{,}\text{v}\right]:=\{{\lambda }_1\text{u}+{\lambda }_2\text{v}:{\lambda }_1\mathrm{,}{\lambda }_2\ge 0$, ${\lambda }_1+{\lambda }_2=1\}$. Egy $K\subseteq {\text{R}}^d$ halmazt akkor hívunk konvexnek, ha tetszőleges $\text{u}\mathrm{,}\text{v}\in K$ pontokra $\left[\text{u}\mathrm{,}\text{v}\right]\subseteq K$ fennáll. Hogyan ,,egészítünk ki'' egy halmazt konvex halmazzá? Azt mondjuk, hogy az ${\text{R}}^d$-beli $H$ halmaznak a $K$ halmaz a konvex burka, ha $K$ konvex, tartalmazza $H$-t, és a legkisebb ilyen halmaz, azaz bármely $L$ konvex halmazra, amely tartalmazza $H$-t igaz, hogy $K\subseteq L$. Belátható, hogy minden halmaznak pontosan egy konvex burka van. Többször használjuk majd a fenti definíció egy következményét: ha az $A\subset {\text{R}}^d$ véges halmaz benne van az $L$ konvex halmazban, akkor $A$ konvex burka is benne van $L$-ben. Egy kétpontú halmaz konvex burka a szakaszuk. Három pontra mi a helyzet? A konvex burkuk nyilván a háromszöglemez, melynek ők a csúcsai. Hogyan kapjuk meg a síkon egy $\text{u}$, $\text{v}$, $\text{w}$ csúcsú háromszöglemez pontjait? A súlypontját például az $\left(\text{u}+\text{v}+\text{w}\right)/3$ képlettel (lássuk be). Kicsit általánosabban: ha veszünk ${\lambda }_1\mathrm{,}{\lambda }_2\mathrm{,}{\lambda }_3\ge 0$ súlyokat, melyek összege 1, akkor a ${\lambda }_1\text{u}+{\lambda }_2\text{v}+{\lambda }_3\text{w}$ helyvektorú pont a háromszöglemez egy pontja (ezt próbáljuk ki, és lássuk is be). Mindezt ennél kicsit általánosabban is elmondhatjuk: adott véges sok ${\text{R}}^d$-beli vektor, ${\text{u}}_1\mathrm{,}{\text{u}}_2\mathrm{,}\text{...}\mathrm{,}{\text{u}}_k$. Ekkor egy $\begin{array}{c}{\displaystyle {\lambda }_1{\text{u}}_1+{\lambda }_2{\text{u}}_2+\text{...}+{\lambda }_k{\text{u}}_k}\end{array}$ alakú kifejezést, ahol ${\lambda }_1\mathrm{,}{\lambda }_2\mathrm{,}\text{...}\mathrm{,}{\lambda }_k\ge 0$ és ${\lambda }_1+{\lambda }_2+\text{...}+{\lambda }_k=1$, konvex kombinációnak hívunk. Az eddigiek szerint, ha rögzítünk két pontot a térben, és vesszük az összes konvex kombinációjukat, akkor pontosan a szakaszuk pontjait kapjuk. Ha pedig rögzítünk három nem egy egyenesre eső pontot, és vesszük az összes konvex kombinációjukat, akkor pontosan annak a háromszöglemeznek a pontjait kapjuk, melynek ők a csúcsai. Igazolható, hogy ha egy $H\subseteq {\text{R}}^d$ halmaz összes véges részhalmazának vesszük az összes konvex kombinációját, akkor éppen $H$ konvex burkát kapjuk.   Feladat: Mutassuk meg, hogy $H$ pontosan akkor konvex, ha tetszőlegesen választva véges sok pontot $H$-ból, az ő konvex burkuk $H$ részhalmaza.   2.3. Konvex politópok. Emlékezzünk vissza arra, hogy mi is egy hipersík ${\text{R}}^d$-ben: Adottak az $a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_d$ számok, melyek közül legalább egy nem nulla, és még egy $a_{d+1}$ szám. Ekkor az $a_1{x}_1+a_2{x}_2+\text{...}+a_d{x}_d+a_{d+1}=0$ egyenletet kielégítő $\left(x_1;\text{...};x_d\right)$ pontok halmaza egy hipersík. Konvex testnek nevezünk egy olyan korlátos konvex halmazt, amely nem része semmilyen hipersíknak (azaz nem ,,lapos''). Definiáljuk a síkbeli konvex sokszög és a térbeli konvex poliéder általánosítását, a $d$-dimenziós konvex politópot úgy, mint véges sok ${\text{R}}^d$-beli pont konvex burka. Ez a definíció nem tökéletes: a térben, ${\text{R}}^3$-ban, például megengedi, hogy vegyük három nem egy egyenesre eső pont konvex burkát, azaz egy háromszöget. Ezt nem szeretnénk 3-dimenziós politópnak hívni, ezért a definíciót kiegészítjük: véges sok, nem egy hipersíkba eső ${\text{R}}^d$-beli pont konvex burkát $d$-dimenziós konvex politópnak hívjuk. Így minden konvex politóp egy konvex test (ehhez lássuk be, hogy valóban korlátos halmaz). A csúcs fogalmát nem definiálom, mert hosszadalmas lenne, szemléletesen meg úgyis érthető. De használni fogom azt a tényt, hogy, ha egy konvex politóp előáll $n$ pont konvex burkaként, akkor csúcsainak halmaza ezen $n$ pont részhalmaza, és így persze legfeljebb $n$ csúcsa van. Miért nem mondom, hogy mind az $n$ pont csúcs? Vegyük például egy kocka 8 csúcsát és a középpontját. A kocka ezen 9 pontnak a konvex burka, mégse szeretném a középpontot is egy csúcsnak hívni. A síkban két pont mindig egy egyenesre esik. Ha veszünk három, nem egy egyenesre eső pontot, a konvex burkuk egy háromszög. A térben három pont mindig egy síkba esik. Ha veszünk négy, nem egy síkba eső pontot, a konvex burkuk egy tetraéder. Belátható, hogy $d$ dimenzióban tetszőleges $d$ pont egy hipersíkba esik (ez a hipersík nem feltétlenül egyértelmű). Aki meg tud oldani sokismeretlenes lineáris egyenletrendszereket, akkor ezt lássa is be. Ha nem, akkor elhihetjük a térbeli eset alapján.   Gondolkodnivaló: ${\text{R}}^d$-ben $d+1$ nem egy hipersíkra eső pont konvex burkának a neve szimplex, ez talán a legegyszerűbb $d$-dimenziós konvex politóp. A szimplexnek persze $d+1$ csúcsa, tehát 0-dimenziós lapja van, és $d+1$ hiperlapja, tehát $\left(d-1\right)$-dimenziós lapja. Ha $0\le k\le d$, akkor hány $k$-dimenziós lapja van? Ehhez a kérdéshez az lenne tisztességes, ha definiálnám egy konvex politóp $k$-dimenziós lapjait, de nem leszek tisztességes, és a lap értelmezését az Olvasó képzeletére bízom.   2.4. Térfogat. Szinte minden készen áll arra, hogy ${\text{R}}^d$-ben geometriával foglalkozzunk, kivéve egy mennyiséget, amelyet a geométerek nagyon kedvelnek, a térfogatot. A területet középiskolában valahogy így vezetik be: egy $a$ oldalhosszú négyzet területe $a^2$. Ha adott egy korlátos konvex síkidom, $K$, akkor vehetünk véges sok átfedés nélküli, a koordinátatengelyekkel párhuzamos oldalú négyzetet $K$-ban, és kiszámolhatjuk az összterületüket. Az így megkapható összterületek szuprémuma $K$ területe. A szuprémum majdnem ugyanazt jelenti, mint a maximum. Pontosabban: $K$ területe 5, ha nem tudok $K$-ba úgy véges sok átfedés nélküli, a koordinátatengelyekkel párhuzamos oldalú négyzetet rajzolni, hogy az összterületük nagyobb legyen, mint 5, de bármilyen 5-nél kisebb $t$ számhoz tudok olyan négyzeteket rajzolni, amelyek összterülete legalább $t$. A háromdimenziós térben hasonlóan definiáljuk egy konvex test térfogatát, így a következő definíció nem meglepő. Legyenek adottak az $a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_d$ és a $b_1\mathrm{,}{b}_2\mathrm{,}\text{...}\mathrm{,}{b}_d$ valós számok, melyekre teljesül, hogy $a_i<b_i$ minden $i$-re. Ekkor az $\begin{array}{c}{\displaystyle }\end{array}$ [a1,b1]×[a2,b2]×...×[ad,bd]:={(x1;x2;...;xd)∈Rd:xi∈[ai,bi]} ${\text{R}}^d$-beli halmazt tengely-párhuzamos téglának hívjuk, melynek térfogata $\begin{array}{c}{\displaystyle \left(b_1-a_1\right)\left(b_2-a_2\right)\cdots \left(b_d-a_d\right)\mathrm{,}}\end{array}$ ami éppen a két- és háromdimenziós eset általánosítása. Legyen adott ${\text{R}}^d$-ben egy korlátos konvex halmaz, $K$. Vegyünk véges sok átfedés nélküli, tengely-párhuzamos téglát $K$-ban, és számoljuk ki az össztérfogatukat. Az így megkapható össztérfogatok szuprémuma $K$ térfogata, amelyet $\text{vol}\left(K\right)$-val jelölünk.   Feladat: Az ${\text{R}}^d$-beli $K$ konvex testet nagyítsuk, vagy kicsinyítsük az origóból $\lambda >0$ aránnyal: $\lambda K:=\left\{\lambda \text{v}:\text{v}\in K\right\}$. Igazoljuk, hogy térfogata így változik: $\begin{array}{c}{\displaystyle \text{vol}\left(\lambda K\right)={\lambda }^d\text{vol}\left(K\right)\mathrm{.}}\end{array}$ (3) Ez éppen a síkban, illetve a térben ismert képlet általánosítása. A térfogatnak még sok szép tulajdonsága van, de azokat nem használom, így most nem sorolom fel.   Tanács: Mindenhez, amiről eddig szó volt, illetve ezután szó esik, bátran készítsünk síkbeli ábrát, esetleg próbáljuk meg elképzelni három dimenzióban, ez hasznos lesz, és az így kapott kép alig csal.   3. Elekes tétele: gömböt a legnehezebb közelíteni Tegyük fel, hogy a $K$ konvex test tartalmazza a $P$ konvex politópot. Hogyan mérjük, hogy $P$ mennyire van közel $K$-hoz? Egy természetes válasz az, hogy nézzük meg a különbségük térfogatát. Bizonyítás nélkül kimondom Macbeath 1951-ben belátott tételét: Legyen $K$ egy ${\text{R}}^d$-beli konvex test, amelynek a térfogata egyenlő az $1$ sugarú gömb, $\text{B}$ térfogatával. Ekkor tetszőleges $n\ge d+1$ természetes számra $K$ tartalmaz olyan $n$-csúcsú konvex politópot, melynek a térfogata legalább akkora, mint a $\text{B}$-ben tartalmazott legnagyobb térfogatú $n$-csúcsú konvex politóp térfogata. Gondoljuk meg, hogy ez éppen azt jelenti, hogy nincs a gömbnél nehezebben közelíthető konvex $K$ test. Mennyire rosszul közelíthető a gömb? Elekes következő tétele szerint igen rosszul.   3.1. tétel (Elekes, 1986). Legyen $P$ egy $n$ csúcsú konvex politóp a $\text{B}$ gömbben. Ekkor $\text{vol}\left(P\right)\le \frac{n}{2^d}\text{vol}\left(\text{B}\right)$.   A tétel $d$ nagy értékére érdekes. Azt mondja, hogy, ha olyan politópot keresek a gömbben, amelynek térfogata a gömb térfogatának mondjuk fele, akkor sok, legalább $2^{d-1}$ csúcsra van szükségem. Például egy hatdimenziós gömb fél térfogatának a ,,körbekerítéséhez'' legalább 32 csúcs kell. Azt nem állítja a tétel, hogy ennyi elég is. Mielőtt $d$ dimenzióban tárgyalnánk Elekes csodálatosan egyszerű, elemi bizonyítását, bizonyítsuk be a következő sík-, illetve térbeli állítást, aminek $d$-dimenziós általánosítása bizonyításának lényege:   Feladat: Adott egy ${\text{v}}_1\mathrm{,}\text{...}\mathrm{,}{\text{v}}_n$ konvex poligon a síkon, ahol jelölje $\text{o}$ az origót. Mutassuk meg, hogy az $\left[\text{o}\mathrm{,}{\text{v}}_i\right]$ szakaszok mint átmérők fölé rajzolt körök teljesen lefedik a poligont. Ugyanez térben: adott egy $P$ konvex poliéder a háromdimenziós térben, melynek csúcsai ${\text{v}}_1\mathrm{,}\text{...}\mathrm{,}{\text{v}}_n$. Igazoljuk, hogy az $\left[\text{o}\mathrm{,}{\text{v}}_i\right]$ szakaszok mint átmérők fölé rajzolt gömbök teljesen lefedik a poliédert.   Ha ezt a két feladatot megoldottuk, akkor nyilván meg tudjuk fogalmazni, és talán be is tudjuk bizonyítani a $d$ dimenziós megfelelőjét. Abból pedig Elekes tétele már könnyen kijön. Most ezt vesszük végig. Elekes gyönyörű igazolása a következő. Jelölje $P$ csúcsait ${\text{v}}_1\mathrm{,}\text{...}\mathrm{,}{\text{v}}_n$. Tekintsük minden egyes ${\text{v}}_i$ csúcsra azt a ${\text{B}}_i$ gömböt, melynek az $\left[\text{o}\mathrm{,}{\text{v}}_i\right]$ szakasz egy átmérője, ahol $\text{o}$ jelöli az origót. A kulcsállítás az, hogy ezen gömbök fedik $P$-t, azaz $\begin{array}{c}{\displaystyle P\subseteq {\bigcup }_{i=1}^n{\text{B}}_i\mathrm{.}}\end{array}$ (4) Tegyük fel, hogy egy $\text{w}$ pont nincs benne a gömbök uniójában. Ekkor, a Thalesz-tétel megfordítását használva az $\sphericalangle \text{o}\text{w}{\text{v}}_i$ szögre kapjuk, hogy $\begin{array}{c}{\displaystyle \sphericalangle \text{o}\text{w}{\text{v}}_i<\pi /2}\end{array}$ (5) minden $i$-re. (Itt csöndben felhasználtuk, hogy két vektor síkjában az általunk skaláris szorzás segítségével definiált szög megegyezik az iskolában tanult szögfogalommal.) Tekintsük azt a $H$ hipersíkot, mely illeszkedik $\text{w}$-re és merőleges a $\text{w}$ vektorra, azaz $H:=\left\{\text{x}\in {\text{R}}^d:\langle \text{x}\mathrm{,}\text{w}\rangle ={|\text{w}|}^2\right\}$ (érdemes meggondolni, hogy valóban ez $H$ egyenlete). A $H$ hipersík két félteret határol, jelölje $H^{-}$ azt a nyílt (tehát $H$-t nem tartalmazó) félteret, amely az origót tartalmazza, azaz $H^{-}:=\left\{\text{x}\in {\text{R}}^d:\langle \text{x}\mathrm{,}\text{w}\rangle <{|\text{w}|}^2\right\}$. Nyilvánvalóan $H^{-}$ egy konvex halmaz (ez is belátandó). Noha $H^{-}$ támaszkodik a $\text{w}$ pontra, $\text{w}\notin H^{-}$.   Feladat: Mutassuk meg, hogy (5) következményeként megkapjuk, hogy ${\text{v}}_i\in H^{-}$ minden $i$-re. Így viszont $P$ benne van a $H^{-}$ konvex halmazban, mert $H^{-}$-beli pontok konvex burka. Ebből következően $\text{w}\notin P$. Ezzel a (4) képletet beláttuk. Azt, hogy ${\text{v}}_i\in H^{-}$, számolással is igazolhatjuk, amit le is írok; ebből látszik majd, hogy a Thálesz-tétel megfordítására sem kell hivatkozni a gondolatmenetben. Mivel $\text{w}$ nincs benne a gömbök uniójában, azért minden $i$-re $|{\text{v}}_i/2-\text{w}|>|{\text{v}}_i|/2$, amiből négyzetreemeléssel kapjuk, hogy $\begin{array}{c}{\displaystyle \langle {\text{v}}_i/2-\text{w}\mathrm{,}{\text{v}}_i/2-\text{w}\rangle ={|{\text{v}}_i|}^2/4+{|\text{w}|}^2-\langle {\text{v}}_i\mathrm{,}\text{w}\rangle >{|{\text{v}}_i|}^2/4.}\end{array}$ Így $\langle {\text{v}}_i\mathrm{,}\text{w}\rangle <{|\text{w}|}^2$, azaz ${\text{v}}_i\in H^{-}$. Végül mivel ${\text{B}}_i$ sugara legfeljebb 1/2, így (3) szerint $\text{vol}\left({\text{B}}_i\right)\le \text{vol}\left(\text{B}\right)/2^d$. Ugyanakkor (4) szerint $\text{vol}\left(P\right)\le {\sum }_{i=1}^n\text{vol}\left({\text{B}}_i\right)$, amivel Elekes tételét beláttuk.   Feladat: Bizonyítsuk be Thalész tételét $d$ dimenzióban, a következő formában: adottak az $\text{u}\ne \text{v}$ pontok ${\text{R}}^d$-ben. Ekkor pontosan azon $\text{w}$ pontokra lesz az $\sphericalangle \text{u}\text{w}\text{v}$ szög derékszög, amelyeknek az $\left(\text{u}+\text{v}\right)/2$ ponttól vett távolsága $|\text{u}-\text{v}|/2$. Amelyek távolsága kisebb, azokra az $\sphericalangle \text{u}\text{w}\text{v}$ szög nagyobb, mint derékszög, amelyek távolsága nagyobb, azokra a szög kisebb, mint derékszög.   4. Gömb közelítése maximális pakolással Végül térjünk vissza a sírkőfaragók bevezetőben említett igazságához: belátjuk, hogy egy elegendően sok csúccsal rendelkező politóp tudja a gömböt jól közelíteni. Ezúttal gömb és politóp közelségét nem a különbség térfogatával mérjük, hanem egy másik, szintén természetes módon. Ha a $P$ konvex politópra teljesül, hogy $\begin{array}{c}{\displaystyle \text{B}\left(\rho \right)\subseteq P\subseteq \text{B}\mathrm{,}}\end{array}$ (6) ahol $0<\rho <1$ egy 1-hez közeli szám, akkor jogosan mondhatjuk, hogy $P$ közel van a gömbhöz.   4.1. tétel. Tetszőleges $d$ dimenzióra és $0<\rho <1$ számra van olyan $n$ csúcsú $P$ politóp, melyre $\left(6\right)$ teljesül, ahol $\begin{array}{c}{\displaystyle n\le {\left(\frac{3-\rho }{1-\rho }\right)}^d\mathrm{.}}\end{array}$ (7)   Tételünk belátásához szükségünk lesz egy alapvető állításra a konvexitás területéről, amely szemléletesen egyáltalán nem meglepő, de pontos bizonyítása mégis meglepően hosszadalmas, ezért mellőzzük. Rögzítsünk egy $0<\rho <1$ számot. Tetszőleges $\text{w}$ pontra a $\text{B}\left(\rho \right)$ gömb határán, azaz olyan pontra, melyre $|\text{w}|=\rho$, jelölje $H_{\text{w}}$ azt a hipersíkot, mely $\text{w}$-ben érinti $\text{B}\left(\rho \right)$-t, azaz amelynek pontosan egy közös pontja van $\text{B}\left(\rho \right)$-val. Belátható, hogy ennek egyenlete $H=\left\{\text{u}\in {\text{R}}^d:\langle \text{w}\mathrm{,}\text{u}\rangle ={\rho }^2\right\}$. Jelölje továbbá $F_{\text{w}}$ azt a $H_{\text{w}}$ által határolt félteret ($H$-t is beleértve), amely nem tartalmazza az origót.   4.2. állítás. Legyen $P$ a ${\text{v}}_1\mathrm{,}\text{...}\mathrm{,}{\text{v}}_n$ pontok konvex burka. Ekkor $P$ akkor és csak akkor fedi az origó középpontú $\rho$ sugarú gömböt, ha a gömb határának bármely $\text{w}$ pontjában húzott érintő hipersíknak az origóval átellenes oldalán is van legalább egy ${\text{v}}_i$. Formálisan: $\text{B}\left(\rho \right)\subset P$ akkor, és csak akkor, ha minden $\text{w}$ pontra, amelyre $|\text{w}|=\rho$, van olyan $i\in \left\{\mathrm{1,}\text{...}\mathrm{,}n\right\}$, amelyre ${\text{v}}_i\in F_{\text{w}}$.   Illusztrációként érdemes belátni az állítást a síkon. Ezután bebizonyítjuk a 4.1. tételt. Egy olyan politópot akarunk találni, amely $n$ pont konvex burkaként áll elő, ahol ezek a pontok egymáshoz nincsenek túl közel, így ,,egyenletesen oszlanak el'' a gömbben. Rögzítünk ezért egy $\delta >0$ számot, amelyet majd később választunk meg, és keresünk a $\text{B}$ gömbben egy olyan ponthalmazt, amelyben bármely két pont távolsága legalább $\delta$, vagy másképpen, a pontok körüli $\delta /2$ sugarú gömbök átfedés nélküliek. Így persze a $\delta /2$ sugarú gömbök uniója benne van a $\text{B}\left(1+\delta /2\right)$ gömbben. Ezt úgy hívják, hogy $\delta /2$ sugarú gömbök pakolása $\text{B}\left(1+\delta /2\right)$-ben. Akárhány gömböt nem vehetünk, mivel egy $\delta /2$ sugarú gömb térfogata ${\left(\delta /2\right)}^d\text{vol}\left(\text{B}\right)$, míg az őket tartalmazó $\text{B}\left(1+\delta /2\right)$-é ${\left(1+\delta /2\right)}^d\text{vol}\left(\text{B}\right)$, lásd (3). Ezért $\begin{array}{c}{\displaystyle n\le {\left(1+\delta /2\right)}^d/{\left(\delta /2\right)}^d\mathrm{.}}\end{array}$ (8) Szeretnénk, ha ezek a kis gömbök, amennyire lehet, ,,kitöltenék'' $\text{B}$-t, ezért egy maximális pakolást veszünk, azaz olyan ${\text{v}}_1\mathrm{,}\text{...}\mathrm{,}{\text{v}}_n$ ponthalmazt $\text{B}$-ben, amelyhez már nem vehető hozzá újabb pont úgy, hogy az mindegyik ${\text{v}}_i$-től legalább $\delta$ távol legyen. Azaz a ${\text{v}}_i$-k körüli $\delta$ sugarú gömbök fedik $\text{B}$-t. Most belátjuk, hogy $\delta =1-\rho$ választással minden $\text{w}$ pontra, amelyre $|\text{w}|=\rho$, van olyan $i\in \left\{\mathrm{1,}\text{...}\mathrm{,}n\right\}$, amelyre ${\text{v}}_i\in F_{\text{w}}$. Ez, a 4.2. állítás szerint elegendő ahhoz, hogy a ${\text{v}}_1\mathrm{,}\text{...}\mathrm{,}{\text{v}}_n$ pontok konvex burka tartalmazza $\text{B}\left(\rho \right)$-t. Tekintsünk egy $\text{w}$ vektort, melynek hossza $\rho$, és tegyük fel, hogy az $F_{\text{w}}$ féltérben nincs ${\text{v}}_i$. Ez esetben a $\delta$ sugarú gömbök mindegyikének a középpontja az $F_{\text{w}}$ féltér komplementer félterében van. Toljuk el az $F_{\text{w}}$ félteret úgy, hogy a határoló hipersík $\delta$ távolsággal ,,beljebb'' kerül a féltérbe, és jelöljük az így kapott félteret $F_{\text{w}}\text{'}$-vel (2. ábra). Ekkor a $\delta$ sugarú gömbök uniója az $F_{\text{w}}\text{'}$ féltér komplementerében van, és így nem tartalmazza a $\text{w}/|\text{w}|\in \text{B}$ pontot. Tehát $\text{w}/|\text{w}|$ minden ${\text{v}}_i$-től legalább $\delta$ távol van, ami ellentmond annak, hogy a pakolásunk maximális. Megkaptuk tehát, hogy a ${\text{v}}_1\mathrm{,}\text{...}\mathrm{,}{\text{v}}_n$ pontok konvex burka tartalmazza a $\text{B}\l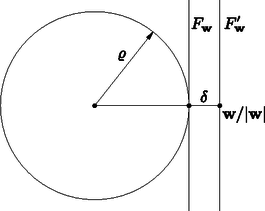eft(\rho \right)$ gömböt.   2. ábra. $\text{B}\left(\rho \right)$ külső érintőféltere $F_{\text{w}}$   Végül (8) garantálja a (7) képlet helyességét, mert $\delta =1-\rho$, amivel a 4.1. tételt beláttuk. Zárásul egy kis számolás, amely összehasonlítja a két tételt. Tíz dimenzióban milyen nagy $n$-nel garantálja a 4.1. tétel olyan $\text{B}$-beli legfeljebb $n$-csúcsú konvex politóp, $P$ létezését, amelynek térfogata legalább $\text{vol}\left(\text{B}\right)/2$? Abból, hogy $\text{B}\left(\rho \right)\subseteq P$, csak annyi következik, hogy ${\rho }^d\text{vol}\left(\text{B}\right)\le \text{vol}\left(P\right)$. Tehát a $\rho =\sqrt[10]{1/2}\approx 0\mathrm{,}933$ sugarú gömböt kell tartalmaznia $P$-nek, amit kb. $n=7\mathrm{,}8\cdot {10}^{14}$ csúccsal tud elérni a tétel. Mindeközben a 3.1. tétel szerint $n$ legalább $512$. A két korlát között van némi hézag. Szerencsére a bemutatottaknál erősebb tételek is ismertek, de az ízüket ez a kettő is remekül visszaadja. Az érdeklődő Olvasónak a magasdimenziós geometriáról a [2] remek könyveket javaslom. A cikk megírásában, a gondolatmenetek tisztázásában sokat segített Surányi László és Lakos Gyula. Köszönöm nekik! A cikk az Emberi Erőforrások Minisztériuma ÚNKP-17-4 kódszámú Új Nemzeti Kiválóság Programjának támogatásával készült.   Hivatkozások [1] Borsányi Ákos: Miért lehet a Fermat-prím oldalú szabályos sokszögeket megszerkeszteni? KöMaL 1994/január: 1. rész; KöMaL 1994/március: 2. rész. [2] J. Pach ‐ P. Agarwal: Combinatorial Geometry (Wiley); J. Matoušek: Lectures on Discrete Geometry (Springer); G. Horváth Á. ‐ Lángi Zs.: Kombinatorikus Geometria (Polygon).