Cím:	Megoldásvázlatok a 2018/6. sz. emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Fridrik Richárd
Füzet:	2018/október, 400 - 409. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Egy szabályos $n$-szög alapú egyenes hasáb lapátlóinak száma, testátlóinak száma és a $24$ valamilyen sorrendben egy számtani sorozat egymást követő tagjait alkotják. Határozzuk meg $n$ lehetséges értékeit.  (11 pont)   Megoldás. A lapátlókból kétfajta van, az oldallapokon és az alaplapokon. Minden oldallapon 2 lapátló van, így ezekből összesen $2n$ van. Az alaplapokon $\frac{n\left(n-3\right)}{2}$ lapátló van, így ezekből összesen $n\left(n-3\right)$ van. Tehát összesen $\begin{array}{c}{\displaystyle 2n+n\left(n-3\right)=n^2-n}\end{array}$ lapátló van. Szemeljük ki az egyik alaplap egy tetszőleges csúcsát. Ebből $n-3$ testátló húzható. Így összesen $n\left(n-3\right)=n^2-3n$ testátló van. Tehát valamilyen sorrendben az $n^2-n$, $n^2-3n$ és a 24 egy számtani sorozat egymást követő tagjait alkotják. Nem a konkrét sorrendjük a lényeges, hanem az, hogy melyik van középen. Ezek alapján 3 esetet vizsgálunk meg és felhasználjuk, hogy számtani sorozatnál egy elem megegyezik a tőle szimmetrikusan elhelyezkedő tagok számtani közepével. 1. eset: Ha $n^2-n$ van középen, akkor $\begin{array}{c}{\displaystyle n^2-n=\frac{n^2-3n+24}{2}\mathrm{,}{n}^2+n-24=\mathrm{0,}}\end{array}$ ennek nincs pozitív egész megoldása. 2. eset: Ha $n^2-3n$ van középen, akkor $\begin{array}{c}{\displaystyle n^2-3n=\frac{n^2-n+24}{2}\mathrm{,}{n}^2-5n-24=\mathrm{0,}}\end{array}$ ennek gyökei $-3$ és 8. Tehát ekkor $n=8$. 3. eset: Ha a 24 van középen, akkor $\begin{array}{c}{\displaystyle 24=\frac{n^2-3n+n^2-n}{2}\mathrm{,}{n}^2-2n-24=\mathrm{0,}}\end{array}$ ennek gyökei $-4$ és 6. Tehát ekkor $n=6$. Tehát $n$ lehetséges értékei 6 és 8. Ellenőrzés. $n=6$ esetén 30 lapátlója és 18 testátlója van a hasábnak és a 18; 24; 30 valóban számtani sorozatot alkotnak. $n=8$ esetén 56 lapátlója és 40 testátlója van a hasábnak és a 24; 40; 56 valóban számtani sorozatot alkotnak.   2. Tekintsük a következő állításokat. $A$: Két irracionális szám összege mindig irracionális. $B$: Van olyan számsorozat, amely korlátos, nem monoton és nem konvergens. $C$: Ha egy ötpontú egyszerű gráf minden csúcsa legalább harmadfokú, akkor biztosan tartalmaz kört. $a)$ Döntsük el, hogy igazak vagy hamisak az állítások. Válaszainkat indokoljuk.   (8 pont) $b)$ Fogalmazzuk meg a $C$ állítás megfordítását. Döntsük el, hogy igaz vagy hamis az állítás megfordítása. Válaszunkat indokoljuk.  (4 pont)   Megoldás. $a)$ Az $A$ állítás hamis, ugyanis $\sqrt[]{2}+\left(-\sqrt[]{2}\right)=0$. Ismert, hogy $\sqrt[]{2}$ irracionális, így nyilván $-\sqrt[]{2}$ is irracionális. A $B$ állítás igaz, pl. $a_n={\left(-1\right)}^n$. Nyilván korlátos, a korlátok $-1$ és 1. Nem monoton és jól ismert, hogy nem konvergens. A $C$ állítás igaz. Mivel az ötpontú gráfunk egyszerű és minden csúcsa legalább harmadfokú, ezért minden csúcsának foka 3 vagy 4. Az nem lehet, hogy minden csúcs foka 3, mert ekkor a fokszámösszeg nem lenne páros. Tehát biztosan van negyedfokú csúcs. Ekkor bármely másik élt berajzolva a gráfba már kör képződik. Megjegyzés. Az ún. Dirac-tétel miatt a $C$-ben lévő gráfban Hamilton-kör is biztosan van. $b)$ A $C$ állítás megfordítása: Ha egy ötpontú egyszerű gráf tartalmaz kört, akkor minden csúcsa legalább harmadfokú. Ez hamis állítás, rengeteg ellenpélda adható. Egy a sok közül, ha berajzolunk egy három hosszú kört és a másik két csúcs izolált pont lesz.   3. Egy négyszög két szomszédos oldalának hossza $3$, illetve 4 cm, közbezárt szögük ${60}^{\circ }$. A négyszög húr- és érintőnégyszög is egyben. $a)$ Mekkora a négyszög másik két oldala?  (7 pont) $b)$ Számítsuk ki a négyszög beírt és köré írt körének sugarát.  (7 pont) (Válaszainkat cm-ben, két tizedesjegyre kerekítve adjuk meg.) 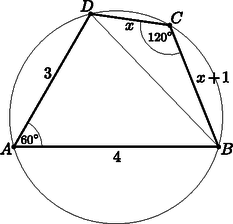  Megoldás. $a)$ Használjuk az ábra jelöléseit. A négyszög $C$ csúcsánál lévő szöge ${120}^{\circ }$, mivel $ABCD$ húrnégyszög. Ha a $CD$ oldal hossza $x$, akkor a $BC$ oldal hossza $x+1$, mivel a négyszög érintőnégyszög. Írjuk fel az $ABD$ háromszögben a koszinusztételt: $\begin{array}{c}{\displaystyle B{D}^2=3^2+4^2-2\cdot 3\cdot 4\cdot \text{cos}{60}^{\circ }\mathrm{,}}\end{array}$ innen $\begin{array}{c}{\displaystyle BD=\sqrt[]{13}\mathrm{.}}\end{array}$     Írjuk fel a koszinusztételt a $BCD$ háromszögben: $\begin{array}{c}{\displaystyle x^2+{\left(x+1\right)}^2-2\cdot x\cdot \left(x+1\right)\cdot \text{cos}{120}^{\circ }=13.}\end{array}$ Innen $x^2+x-4=0$, a számunkra megfelelő gyök $\begin{array}{c}{\displaystyle x=\frac{\sqrt[]{17}-1}{2}\approx 1\mathrm{,}56\text{ cm, így}x+1=\frac{\sqrt[]{17}+1}{2}\approx 2\mathrm{,}56\text{cm}\mathrm{.}}\end{array}$ Tehát a hiányzó oldalak két tizedesjegyre kerekítve 1,56 cm és 2,56 cm hosszúak. $b)$ A beírt kör sugarát a $T=rs$ összefüggésből határozzuk meg.(Ez a képlet minden érintősokszögre igaz.) Mivel $\begin{array}{c}{\displaystyle s=\frac{3+4+1\mathrm{,}56+2\mathrm{,}56}{2}=5\mathrm{,}56\text{cm}}\end{array}$ és $\begin{array}{c}{\displaystyle T_{ABCD}=T_{ABD}+T_{BCD}=\frac{3\cdot 4\cdot \text{sin}{60}^{\circ }}{2}+\frac{1\mathrm{,}56\cdot 2\mathrm{,}56\cdot \text{sin}{120}^{\circ }}{2}\approx 6\mathrm{,}93{\text{cm}}^2\mathrm{,}}\end{array}$ ezért $r=\frac{T}{s}\approx 1\mathrm{,}25$ cm. A négyszög köré írható körének sugara megegyezik az $ABD$ háromszög köré írható körének sugarával, így az $R=\frac{abc}{4T}$ képlet segítségével kapjuk, hogy $\begin{array}{c}{\displaystyle R=\frac{3\cdot 4\cdot \sqrt[]{13}}{4\cdot \frac{3\cdot 4\cdot \text{sin}{60}^{\circ }}{2}}\approx 2\mathrm{,}08\text{cm}\mathrm{.}}\end{array}$ Tehát a beírt kör sugara 1,25 cm, míg a köré írható kör sugara 2,08 cm. Megjegyzés. A köré írható kör sugarát az $R=\frac{a}{2\text{sin}\alpha }$ összefüggésből is meghatározhattuk volna.   4. $a)$ Mutassuk meg, hogy az $f\left(x\right)=\frac{2^x-1}{2^x+1}$ függvény páratlan és korlátos függvény.  (7 pont) $b)$ Egy gömb alakú higanycsepp $n$ egyforma, kisebb cseppre esett szét. Ezáltal a kis cseppek összfelszíne éppen négyszerese lett az eredeti higanycsepp felszínének. Határozzuk meg $n$ értékét.  (7 pont)   Megoldás. $a)$ A függvény értelmezési tartománya a valós számok halmaza. Azt kell megmutatni, hogy tetszőleges valós $x$-re $f\left(-x\right)=-f\left(x\right)$. Mivel $f\left(x\right)=\frac{2^x-1}{2^x+1}$, ezért $\begin{array}{c}{\displaystyle f\left(-x\right)=\frac{2^{-x}-1}{2^{-x}+1}=\frac{1-2^x}{1+2^x}=-f\left(x\right)\mathrm{.}}\end{array}$ Tehát a függvény páratlan. Mivel a függvény páratlan, ezért elég megmutatni, hogy $x\ge 0$ esetén korlátos. Azt állítjuk, hogy tetszőleges nemnegatív $x$-re $f\left(x\right)<1$. Valóban: $\begin{array}{c}{\displaystyle \frac{2^x-1}{2^x+1}=1-\frac{2}{2^x+1}<1.}\end{array}$ Tehát a függvény korlátos, korlátok: $-1$ és 1. $b)$ Jelöljük a nagy gömb sugarát $R$-rel, a kicsi gömbök sugarát $r$-rel. A szétesés során a higany térfogata nem változik, tehát $\begin{array}{c}{\displaystyle n\cdot \frac{4r^3\pi }{3}=\frac{4R^3\pi }{3}\mathrm{.}}\end{array}$ Innen $R=\sqrt[3]{n}\cdot r$, azaz $\frac{r}{R}=\frac{1}{\sqrt[3]{n}}$. Az összfelszín a négyszeresére növekedett, tehát $\frac{n\cdot 4r^2\pi }{4R^2\pi }=4$, azaz $n\cdot {\left(\frac{r}{R}\right)}^2=4$. Innen $n\cdot \frac{1}{\sqrt[3]{n^2}}=4$, $\sqrt[3]{n}=4$, $n=64$ adódik. Tehát a higanycsepp 64 részre esett szét. Ellenőrzés a feladat szövege alapján.   II. rész     5. $a)$ Cinkelt érmét szeretnénk készíteni. A ,,Trükkös hatos'' nevű játékban akkor nyerünk, ha az érme hatszori feldobásakor pontosan négyszer lesz fej és kétszer írás. Milyen módon cinkeljük az érmét (vagyis mekkora legyen a fej dobásának a valószínűsége), ha a lehető legnagyobb valószínűséggel szeretnénk nyerni?  (8 pont) $b)$ Legfeljebb hány különböző pozitív prímszám adható meg úgy, hogy közülük bármely három összege is prímszám legyen? Adjunk példát a maximális elemszámra és mutassuk meg, hogy több prímszámot nem tudunk megadni a kívánt módon.  (8 pont)   Megoldás. $a)$ Legyen a fej dobásának valószínűsége $p$, az írásé $1-p$, ahol $p\in \left[0;1\right]$. A binomiális eloszlás ismert képlete szerint $\begin{array}{c}{\displaystyle p\left(\text{6 dobásból négyszer fej, kétszer írás}\right)=\left(\genfrac{}{}{0ex}{}{6}{4}\right)\cdot p^4\cdot {\left(1-p\right)}^2\mathrm{.}}\end{array}$ Ez akkor veszi fel maximumát, amikor $p^4\cdot {\left(1-p\right)}^2=p^6-2p^5+p^4$ maximális. I. megoldás. Tehát az alábbi függvény maximumhelyét kell megkeresnünk: $f:\left[0;1\right]\to R$, $f\left(p\right)=p^6-2p^5+p^4$. A szélsőértéket derivált segítségével határozzuk meg: $\begin{array}{c}{\displaystyle f\text{'}\left(p\right)=6p^5-10p^4+4p^3\mathrm{.}}\end{array}$ Megoldjuk az $f\text{'}\left(p\right)=0$ egyenletet: $\begin{array}{c}{\displaystyle 2p^3\cdot \left(3p^2-5p+2\right)=\mathrm{0,}}\end{array}$ innen a gyökök $p_1=0$; $p_2=\frac{2}{3}$; $p_3=1$. $f\text{'}\text{'}\left(p\right)=30p^4-40p^3+12p^2$ és $f\text{'}\text{'}(\frac{2}{3})<0$ adódik, tehát $p=\frac{2}{3}$-ban helyi maximuma van a függvénynek. Mivel $f\left(0\right)=f\left(1\right)=0$, ezért $p=\frac{2}{3}$ globális maximumhelye is a függvénynek. Megjegyzés. A függvény menetének vizsgálata történhet táblázatos módszerrel is. II. megoldás. A maximum helyét deriválás nélkül, közepekkel is meg tudjuk határozni: $\begin{array}{c}{\displaystyle \sqrt[6]{\frac{p}{2}\cdot \frac{p}{2}\cdot \frac{p}{2}\cdot \frac{p}{2}\mathrm{.}\left(1-p\right)\cdot \left(1-p\right)}\le \frac{4\cdot \frac{p}{2}+2\cdot \left(1-p\right)}{6}=\frac{1}{3}\mathrm{,}}\end{array}$ azaz $p^4\cdot {\left(1-p\right)}^2\le \frac{16}{729}$ és egyenlőség fennállása $\frac{p}{2}=1-p$, $p=\frac{2}{3}$ esetén. $b)$ A 2 nem szerepelhet a kiválasztott prímszámok között, mivel másik két páratlan prímet hozzáadva 2-nél nagyobb páros eredményt kapunk, így nem lehet prím. Tehát csak páratlan prímekkel dolgozunk. A prímeket 3-mal való osztási maradék alapján három csoportba soroljuk: az első csoportban lesznek a 3-mal osztva 1, a másodikban a 3-mal osztva 2 maradékot adó prímek és a harmadik csoportba egyedül a 3 kerül, mivel az egyedüli prím, ami osztható 3-mal, maga a 3. Világos, hogy az első és a második csoportból is legfeljebb két elemet választhatunk, mivel ha legalább hármat vennénk belőlük, összegük 3-nál nagyobb, 3-mal osztható lenne, így nem lenne prím. Az is könnyen látszik, hogy ha mindhárom csoportból választunk, akkor összegük ismét 3-mal osztható lenne. Tehát legfeljebb négy prímet tudunk a feltételeknek megfelelően megadni és azt is csak úgy, ha két-két elemet választunk az első és a második csoportból. Némi próbálkozás után megtalálhatjuk pl. az alábbi prímeket: 7; 11; 13; 23. Könnyű ellenőrizni, hogy ezek valóban jók.   6. $a)$ Egy családban három gyerek van: Anna, Béla és Csaba. Minden nap kisorsolják, hogy ki vigye le sétáltatni kutyájukat, Buksit (egy kalapba teszik egy-egy cédulára írva a nevüket, majd húznak egy cédulát). Hány olyan sorsolás van, amelynél egy hetes időszakot véve, minden gyerek sorra kerül a kutyasétáltatás során?  (9 pont) $b)$ Igazoljuk (teljes indukcióval vagy más módszerrel), hogy ha $n\ge 9$ pozitív egész szám, akkor $2^n>32n$.  (7 pont)   Megoldás. $a)$ I. megoldás. Azon sorsolások számát, amikor mindenki sorra kerül, komplementer segítségével adjuk meg. Az összes sorsolások száma $3^7=2187$. A komplementer azokat az eseteket tartalmazza, amikor 1 vagy pontosan 2 gyerek kerül sorra. Azoknak az eseteknek a száma, amikor 1 gyerek kerül sorra, nyilván 3. Azoknak az eseteknek a száma, amikor pontosan 2 gyerek kerül sorra, $\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{3}{2}\right)\cdot \left(2^7-2\right)=\mathrm{378,}}\end{array}$ ugyanis először kiválasztjuk, hogy melyik 2 gyerek fog sorra kerülni a hét folyamán, ez $\left(\genfrac{}{}{0ex}{}{3}{2}\right)$. Ezután a kiválasztott 2 gyereket $2^7$-féleképpen lehetne beosztani a héten, de ezekből az esetekből 2 nem lesz jó, amikor csak az egyikük van kisorsolva. Tehát $2187-378-3=1806$ olyan sorsolás van, amikor mindhárom gyerek sorra kerül. II. megoldás. A feladatot úgy is megoldhatjuk, hogy megnézzük, a 7-et hányféleképpen lehet felbontani pozitív egész számok összegére. Négy eset adódik: 1. eset: $5+1+1$, ebből $\left(\genfrac{}{}{0ex}{}{3}{1}\right)\cdot 7\cdot 6=126$ sorsolás van; 2. eset: $4+2+1$, ebből $3!\cdot \left(\genfrac{}{}{0ex}{}{7}{4}\right)\cdot \left(\genfrac{}{}{0ex}{}{3}{2}\right)=630$ sorsolás van; 3. eset: $3+3+1$, ebből $\left(\genfrac{}{}{0ex}{}{3}{1}\right)\cdot \left(\genfrac{}{}{0ex}{}{7}{3}\right)\cdot \left(\genfrac{}{}{0ex}{}{4}{3}\right)=420$ sorsolás van; 4. eset: $3+2+2$, ebből $\left(\genfrac{}{}{0ex}{}{3}{1}\right)\cdot \left(\genfrac{}{}{0ex}{}{7}{3}\right)\cdot \left(\genfrac{}{}{0ex}{}{4}{2}\right)=630$ sorsolás van. Összesen $126+630+420+630=1806$ sorsolás lehetséges. $b)$ Teljes indukcióval bizonyítunk. $n=9-$re: $2^9>32\cdot 9$ igaz, hiszen $512>288$. Tegyük fel, hogy $n$-re igaz az állítás, azaz ha $n\ge 9$ rögzített, akkor $2^n>32n$. Belátjuk, hogy ekkor $\left(n+1\right)$-re is igaz az állítás, azaz $2^{n+1}>32\cdot \left(n+1\right)$. Valóban: $2^{n+1}=2\cdot 2^n>2\cdot 32n=32\cdot 2n=32\cdot \left(n+n\right)\ge 32\cdot \left(n+1\right)$, tehát $2^{n+1}>32\cdot \left(n+1\right)$. Az első becslésnél az indukciós feltevést használtuk fel, míg a másodiknál azt, hogy $n\ge 1$. Ezzel az állítást beláttuk.   7. $a)$ Oldjuk meg a valós számok halmazán az alábbi egyenletet:  (8 pont) $\begin{array}{c}{\displaystyle \text{tg}x\cdot \text{sin}4x=\frac{1}{2}\mathrm{.}}\end{array}$ $b)$ Adjuk meg azokat a $t$ pozitív egész számokat, amelyekre a fenti egyenletnek a $\left[2018;t\right]$ intervallumon pontosan $2018$ darab valós megoldása van. Számításaink során a $\pi$ minél pontosabb értékével számoljunk.  (8 pont)   Megoldás. $a)$ Először is tegyünk kikötést az egyenletben szereplő kifejezésekre. $\text{cos}x\ne 0$, azaz $x\ne \frac{\pi }{2}+k\pi$, ahol $k\in \text{Z}$. Az egyenlet megoldása során felhasználjuk a $\text{sin}2x=2\text{sin}x\text{cos}x$ és a $\text{cos}2x=1-2\text{sin}{}^{2}x$ addíciós képleteket. ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{tg}x\cdot \text{sin}4x=\frac{1}{2}\mathrm{,}\frac{\text{sin}x}{\text{cos}x}\cdot 2\text{sin}2x\cdot \text{cos}2x=\frac{1}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{\text{sin}x}{\text{cos}x}\cdot 2\cdot 2\text{sin}x\text{cos}x\cdot \left(1-2\text{sin}{}^{2}x\right)=\frac{1}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{sin}{}^{2}x\cdot \left(1-2\text{sin}{}^{2}x\right)=\frac{1}{8}\mathrm{,}16\text{sin}{}^{4}x-8\text{sin}{}^{2}x+1=\mathrm{0,}}\hfill \\ \hfill {\displaystyle {\left(4\text{sin}{}^{2}x-1\right)}^2=\mathrm{0,}\text{sin}{}^{2}x=\frac{1}{4}\mathrm{,}}\hfill \end{array}}$ $\text{sin}x=\frac{1}{2}$ vagy $\text{sin}x=-\frac{1}{2}$. Ezen egyenletek megoldásait összevonva adódnak a megoldások: $x_1=\frac{\pi }{6}+k\pi$ és $x_2=-\frac{\pi }{6}+k\pi$, ahol $k;l\in \text{Z}$. Ezek a megoldások nem ellentmondóak a kikötéssel. Ellenőrzés vagy végig ekvivalens átalakításokra való hivatkozás. $b)$ Írjuk le egymás után az egyenlet pár megoldását: $\begin{array}{c}{\displaystyle \text{...};-\frac{7\pi }{6};-\frac{5\pi }{6};-\frac{\pi }{6};\frac{\pi }{6};\frac{5\pi }{6};\frac{7\pi }{6};\frac{11\pi }{6};\frac{13\pi }{6};\text{...}}\end{array}$ Észre lehet venni, hogy a megoldások a $\pi$ egész számú többszöröseitől éppen $\frac{\pi }{6}$ távolságra szimmetrikusan helyezkednek el. Mivel $642\frac{1}{6}\pi <2018$ és $642\frac{5}{6}\pi >2018$, így az első megoldáspár, ami beleesik a kívánt intervallumba: $642\frac{5}{6}\pi$ és $643\frac{1}{6}\pi$. Mivel 2018 darab megoldásnak kell benne lennie az intervallumban és a megoldásokat párosával érdemes felírni, ezért ‐ mivel az első megoldáspár a $643\pi$-re szimmetrikus ‐ az 1009. pár az $1651\pi$-re lesz szimmetrikus: $1650\frac{5}{6}\pi$ és $1651\frac{1}{6}\pi$. Tehát olyan $t$ pozitív egész számot kell megadni, amelyre $1651\frac{1}{6}\pi \in \left[2018;t\right]$ és $1651\frac{5}{6}\pi \notin \left[2018;t\right]$. Innen adódnak $t$ lehetséges értékei: $t_1=5188$ és $t_2=5189$.   8. Húzzunk érintőket az $y=x^2$ parabola $A\left(-1;1\right)$ és $B\left(2;4\right)$ pontjaiba. $a)$ Írjuk fel az érintők egyenletét.  (3 pont) $b)$ Mutassuk meg, hogy az érintők a $C(\frac{1}{2};-2)$ pontban metszik egymást.   (2 pont) A parabola két részre osztja az $ABC$ háromszöget, egy konvexre és egy konkávra. $c)$ Számítsuk ki az $ABC$ háromszög területét.  (5 pont) $d)$ Határozzuk meg a konvex és a konkáv alakzat területét.  (6 pont)   Megoldás. $a)$ I. megoldás. Az érintő meredekségét derivált segítségével határozzuk meg: $y\text{'}=2x$. Az $e$ egyenes egyenlete $y-1=-2\left(x+1\right)$, azaz $y=-2x-1$, az $f$ egyenes egyenlete $y-4=4\left(x-2\right)\mathrm{,}$ azaz $y=4x-4$. II. megoldás. Az érintők egyenletét $y=mx+b$ alakban is kereshettük volna. Felhasználjuk, hogy a pont illeszkedik az egyenesre és felírjuk az érintési feltételt, mely szerint a kapott másodfokú egyenlet diszkriminánsa 0. Az $e$ egyenletét így meghatározva: $y=mx+b$, $A\in e$, így $1=-m+b$, $b=1+m$, innen $y=mx+1+m$. Ez az $e$ egyenes és az $y=x^2$ parabola érintik egymást, így az  $x^2=mx+1+m\mathrm{,}$ azaz $x^2-mx-\left(1+m\right)=0$ egyenlet diszkriminánsa 0, azaz $m^2+4\left(1+m\right)=0$, innen $m=-2$ és $y=-2x-1$ adódik. Az $f$ egyenlete ugyanígy adódik. $b)$ Meg kell oldanunk az $y=-2x-1$ és az $y=4x-4$ egyenletekből álló egyenletrendszert. Innen $-2x-1=4x-4$, $x=\frac{1}{2}$ és $y=-2$. $c)$ Az $ABC$ háromszög köré egy téglalapot rajzolunk. 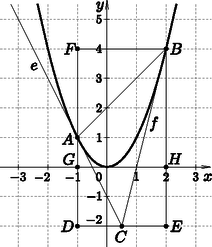${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_{ABC}}& {\displaystyle =T_{DEBF}-T_{ACD}-T_{BCE}-T_{ABF}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =18-\frac{9}{4}-\frac{9}{2}-\frac{9}{2}=\frac{27}{4}\mathrm{.}}\hfill \end{array}}$ Megjegyzés. Az $ABC$ háromszög területét pl. úgy is kiszámolhattuk volna, hogy (skaláris szorzattal vagy koszinusztétellel) kiszámoljuk a $C$-nél lévő szögét és az $AC$, $BC$ oldalakat, majd használjuk a trigonometrikus területképletet.       $d)$ A konvex alakzat területét úgy kapjuk meg, hogy kiszámoljuk az $ABHG$ derékszögű trapéz területét és abból kivonjuk a parabola alatti területet (melyet integrálással kapunk meg). $\begin{array}{c}{\displaystyle T_{ABHG}=\frac{1+4}{2}\cdot 3=\frac{15}{2}\mathrm{,}\underset{-1}{\overset{2}{\int }}{x}^2\text{d}x={\left[\frac{x^3}{3}\right]}_{-1}^2=3\mathrm{,}{T}_{\text{konvex}}=\frac{15}{2}-3=\frac{9}{2}\mathrm{.}}\end{array}$ Innen a konkáv alakzat területét már könnyen megkapjuk: $T_{\text{konkáv}}=\frac{27}{4}-\frac{9}{2}=\frac{9}{4}$. Megjegyzés. Be lehet látni, hogy ha az eredeti $A$ és $B$ pontok tetszőlegesek, akkor is fennáll, hogy $T_{\text{konvex}}=2\cdot T_{\text{konkáv}}$.   9. A Bástya SE sakkcsapata nemrég indult először a nemzeti csapatbajnokságban. Egy találkozón $2$ csapat küzd meg egymással, mindkét csapat $12$ játékossal játszik. Ennek a $12$ játékosnak van egy előre rögzített erősségi sorrendje és az egyik csapat legerősebbje játszik a másik csapat legerősebbjével, a második legerősebbek is egymással, stb. Így egy találkozón $12$ partira kerül sor. Egy partinak $3$ kimenetele lehet: győzelem esetén $1$, vereség esetén $0$, míg döntetlen esetén fél pontot kap a játékos. Tegyük fel, hogy egy-egy parti kimenetele nem függ a játékosok sakktudásától, mindegyik kimenetel egyformán valószínű. A csapat által elért pontszámot úgy kapjuk meg, hogy összeadjuk az egyes csapaton belüli játékosok által elért pontokat. $a)$ Mutassuk meg, hogy csak úgy lehet döntetlen (azaz amikor $6$ pontot ér el mindkét csapat) egy találkozó, ha egy csapaton belül ugyanannyiszor nyernek és veszítenek.  (2 pont) $b)$ Mennyi annak a valószínűsége, hogy ‐ a fenti feltételek mellett ‐ a Bástya SE döntetlent ér el első mérkőzésén?  (7 pont) $c)$ Mennyi annak a valószínűsége, hogy az első három találkozójuk döntetlen lesz és a negyedik meccset megnyerik? Az egyes találkozókon elért eredményeket egymástól függetleneknek tekinthetjük. Válaszainkat négy tizedesjegyre kerekítve adjuk meg.  (2 pont) A csapat legjobb pontszerzője 9 partit játszott az idény folyamán. Az általa szerzett pontok átlaga $\frac{2}{3}$, míg a szórásnégyzete $\frac{1}{6}$. $d)$ Határozzuk meg, hogy a játékos hány partiban nyert, vesztett illetve ért el döntetlent.  (5 pont)   Megoldás. $a)$ I. megoldás. A csapat egy találkozón összesen 12 partit játszik, ebből legyen $x$ nyerése, $y$ vesztése és $12-x-y$ döntetlene. Az összpontszámnak 6-nak kell lennie: $\begin{array}{c}{\displaystyle x\cdot 1+y\cdot 0+\left(12-x-y\right)\cdot \frac{1}{2}=\mathrm{6,}\text{azaz}6+\frac{x}{2}-\frac{y}{2}=\mathrm{6,}}\end{array}$ tehát $x=y$. Pont ezt kellett megmutatni. II. megoldás. Vegyük azt az esetet, amikor mind a 12 partiban döntetlent érnek el. Ekkor teljesül, hogy ugyanannyi vereség és győzelem van. Ha egy döntetlen helyett pl. egy nyerés lenne, akkor kell egy vesztés is, hogy az átlagos pontszám ne változzon. Tehát a nyerések és vesztések száma az eredeti 0-hoz képest mindig ugyanannyival növekszik. Pont ezt kellett megmutatni. $b)$ Az előző feladatrészből kiderül, hogy mely esetekben lehet döntetlen a találkozó kimenetele. Ezeknek az eseményeknek a valószínűségeit meghatározzuk, majd a végén összeadjuk ezeket. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle P\left(12\text{ döntetlen}\right)}& {\displaystyle =\frac{1}{3^{12}};}\hfill \\ \hfill {\displaystyle P\left(10\text{ döntetlen}\mathrm{,}1\text{ nyerés}\mathrm{,}1\text{ vesztés}\right)}& {\displaystyle =\frac{12\cdot 11}{3^{12}}=\frac{132}{3^{12}};}\hfill \\ \hfill {\displaystyle P\left(8\text{ döntetlen}\mathrm{,}2\text{ nyerés}\mathrm{,}2\text{ vesztés}\right)}& {\displaystyle =\frac{\left(\genfrac{}{}{0ex}{}{12}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{10}{2}\right)}{3^{12}}=\frac{2970}{3^{12}};}\hfill \\ \hfill {\displaystyle P\left(6\text{ döntetlen}\mathrm{,}3\text{ nyerés}\mathrm{,}3\text{ vesztés}\right)}& {\displaystyle =\frac{\left(\genfrac{}{}{0ex}{}{12}{3}\right)\cdot \left(\genfrac{}{}{0ex}{}{9}{3}\right)}{3^{12}}=\frac{18480}{3^{12}};}\hfill \\ \hfill {\displaystyle P\left(4\text{ döntetlen}\mathrm{,}4\text{ nyerés}\mathrm{,}4\text{ vesztés}\right)}& {\displaystyle =\frac{\left(\genfrac{}{}{0ex}{}{12}{4}\right)\cdot \left(\genfrac{}{}{0ex}{}{8}{4}\right)}{3^{12}}=\frac{34650}{3^{12}};}\hfill \\ \hfill {\displaystyle P\left(2\text{ döntetlen}\mathrm{,}5\text{ nyerés}\mathrm{,}5\text{ vesztés}\right)}& {\displaystyle =\frac{\left(\genfrac{}{}{0ex}{}{12}{5}\right)\cdot \left(\genfrac{}{}{0ex}{}{7}{5}\right)}{3^{12}}=\frac{16632}{3^{12}};}\hfill \\ \hfill {\displaystyle P\left(0\text{ döntetlen}\mathrm{,}6\text{ nyerés}\mathrm{,}6\text{ vesztés}\right)}& {\displaystyle =\frac{\left(\genfrac{}{}{0ex}{}{12}{6}\right)}{3^{12}}=\frac{924}{3^{12}}\mathrm{.}}\hfill \end{array}}$ Ezért $P\left(\text{döntetlen}\right)=\frac{73789}{3^{12}}\approx 0\mathrm{,}1388$. $c)$ Szimmetria okok miatt egyenlő annak a valószínűsége, hogy az adott csapat megnyeri vagy éppen elveszíti a találkozót. A döntetlen valószínűségét már kiszámoltuk, így a nyerés valószínűsége: $\begin{array}{c}{\displaystyle P\left(\text{megnyeri a találkozót a csapat}\right)=\frac{1-P\left(\text{döntetlen}\right)}{2}=0\mathrm{,}4306.}\end{array}$ Mivel a találkozók kimenetelei egymástól függetleneknek tekinthetők, ezért a valószínűség: $\begin{array}{c}{\displaystyle P\left(\text{első három döntetlen, 4.-et megnyerik}\right)=0\mathrm{,}{1388}^3\cdot 0\mathrm{,}4306\approx 0\mathrm{,}00115.}\end{array}$ Tehát a keresett valószínűség kb. 0,0012. $d)$ A legjobb pontszerző a 9 meccsből nyerjen $x$-et, döntetlent érjen el $y$ partiban és $9-x-y$ partit veszítsen el. Ekkor az átlag: $\begin{array}{c}{\displaystyle \frac{x\cdot 1+y\cdot \frac{1}{2}+\left(9-x-y\right)\cdot 0}{9}=\frac{2}{3}\mathrm{,}}\end{array}$ innen $x+\frac{y}{2}=6$ adódik. A szórásnégyzet: $\begin{array}{c}{\displaystyle \frac{x\cdot 1^2+y\cdot (\frac{1}{2}{)}^2+\left(9-x-y\right)\cdot 0^2}{9}-{\left(\frac{2}{3}\right)}^2=\frac{1}{6}}\end{array}$ innen $x+\frac{y}{4}=\frac{11}{2}$ adódik. A két kapott egyenletből álló egyenletrendszert megoldva $x=5$, $y=2$, $9-x-y=2$ adódik. Tehát a legjobb pontszerző 5 partit nyert, 2-t elvesztett és 2-ben döntetlent ért el. Ellenőrzés a feladat szövege alapján.