Kezdőlap


Cím:	Síkbeli elektromos vezetési problémák I. rész
Szerző(k):	Elek Péter , Szász Krisztián
Füzet:	2019/január, 41 - 46. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek, Áramkörök

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Síkbeli elektromos vezetési problémák
I. rész (matematikai előkészítés)

Bevezetés

Síkbeli vezetési jelenség során egy vékony síklapban létrejövő áramlást vizsgálunk. Ebben az esetben azt mondhatjuk, hogy a síkra merőlegesen nincs áramlás, vagy az áramlást leíró fizikai mennyiségek nem függenek ettől az iránytól. Ilyen jelenség lehet például az elektromos vezetés, a hővezetés vagy folyadék áramlása. Egy ilyen áramlási problémában az a feladat, hogy meghatározzuk a kialakuló kétdimenziós (síkbeli) áramlási teret, tehát az elektromos vezetés esetén az elektromos erővonalakat, hővezetésnél a hőáram áramvonalait, folyadék áramlásakor a sebességteret, vagyis az áramvonalak alakját.
A feladat megoldása általában nehéz. Sok esetben különböző határfeltételeknek kell teljesülni: a síklap (lemez) nem végtelen kiterjedésű, adott szögű hajlat van benne, esetleg a vizsgálandó tartomány lyukas. Azonban, ha az összenyomhatatlannak tekinthető folyadék áramlása stacionárius, azaz a lemezen kialakult áramlási tér időben nem változik, egy ügyesen választott leképezéses módszerrel sokkal könnyebben megadhatjuk az áramlás leírását. Ez azt jelenti, hogy egy megfelelő transzformációval a vizsgálandó áramlás egy másik, már ismert (vagy könnyebben leírható) áramlásba vihető át, így arra visszavezetve az eredeti probléma is megoldhatóvá válik. Megmutatható, hogy stacionárius esetben a megoldandó egyenletek mindhárom témakörben alakilag megegyeznek, így ez a módszer mindhárom esetben alkalmazható. A továbbiakban csak elektromos vezetéssel foglalkozunk, hővezetési és folyadékáramlási problémákat ‐ terjedelmi okokból ‐ nem tárgyalunk.
A leképezéses módszer a témakör szokásos tárgyalásában a komplex számok algebrai tulajdonságait és a komplex változós függvények differenciálszámítását használja fel, ami meghaladja a középiskolai matematika tananyagot. Ezért a cikkünkben ‐ rendhagyó módon ‐ egy egyszerűbb utat választunk: a leképezés geometriai tulajdonságait fogjuk vizsgálni, és csak elemi matematikai ismereteket várunk el az Olvasótól. Nem fogjuk az elektromos áram eloszlásának minden részletét meghatározni, hanem csak azt vizsgáljuk meg, hogy a lemezbe egy vagy több ponton be-, illetve kivezetett áram hatására (különböző geometriai elrendezések esetén) a lemez két kiválasztott pontja között mekkora feszültség alakul ki. Az ilyen feladatokra is alkalmazható az említett leképezéses eljárás, amihez egyszerűbb esetekben nincs szükség komplex változós függvények ismeretére.
A továbbiakban (teljesen általánosan vetve fel a kérdést) megvizsgáljuk, hogy milyen tulajdonságú transzformációk alkalmasak egymástól látszólag teljesen független síkbeli árameloszlások közötti kapcsolat leírására. Miután erre a kérdésre választ kaptunk, pontos matematikai képletekkel konkrétan megadunk a legfontosabb transzformációtípusok közül néhányat, majd cikkünk II. részében bemutatjuk, hogyan alkalmazhatók ezek a transzformációk bizonyos fizikai problémák megoldásánál.

Arány- és szögtartó transzformációk

Egy elektromosan vezető síklemezbe, amely lehet véges kiterjedésű, vagy akár ,,végtelen'' nagy, bizonyos helyeken áramokat vezetünk be, illetve áramokat vezetünk el róla. A lemez homogén, vastagsága

δ

, fajlagos ellenállása

ϱ

.
Tételezzük fel, hogy ismerjük a kialakuló árameloszlást, vagyis a

j (r)

áramsűrűséget, valamint az elektromos potenciál

Φ (r)

függvényét. Mindezeket a mennyiségeket egy alkalmasan választott derékszögű

(x, y)

koordináta-rendszerben adhatjuk meg (lásd az 1. ábra bal oldali részét), de használhatjuk az

(r, φ)

síkbeli polárkoordinátákat is. Válasszuk ki az árameloszlásnak egy kicsiny, téglalap alakúnak tekinthető részét, amit két egymástól csak kicsit eltérő ekvipotenciális görbe és két közeli áramvonal határol. Legyenek a téglalap oldalai

a

és

b

, és jelöljük a

P

és

S

pontok közötti szakaszon átfolyó áram erősségét

I

-vel. (Ugyancsak

I

erősségű áram folyik a

Q

és az

R

pontok között is, hiszen az áramlási kép stacionárius, a töltések sehol nem halmozódhatnak fel egyre növekvő mértékben.)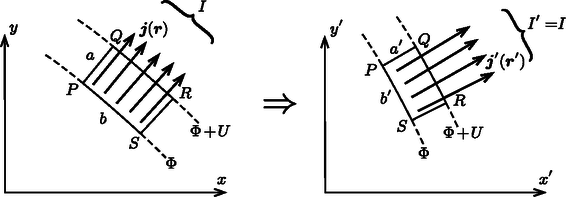

1. ábra

Az áramerősség az áramsűrűséggel (vagyis az egységnyi felületen átfolyó árammal), az áramsűrűség az elektromos térerősséggel, a térerősség pedig a potenciálkülönbséggel fejezhető ki:

\begin{matrix} I = | j | \cdot b δ, j (r) = \frac{1}{ϱ} E, | E | = \frac{U}{a}, \end{matrix}

így tehát a

P

és

S

pontok közötti

b \cdot δ

nagyságú felületen átfolyó áram erőssége:

\begin{matrix} I = \frac{U δ}{ϱ} \cdot \frac{b}{a} . \end{matrix}

Ha valamilyen transzformáció (leképezés) az áram- és potenciáleloszlást átviszi az

(x', y')

koordinátarendszerben megadható

j' (r')

árameloszlásba (lásd az 1. ábra jobb oldali részét), akkor a vizsgált kicsiny tartományon átfolyó áram erőssége:

\begin{matrix} I' = \frac{U δ}{ϱ} \cdot \frac{b'}{a'} . \end{matrix}

Felhasználtuk, hogy a transzformált áramsűrűség-vektorok merőlegesek a transzformált ekvipotenciális görbékre, tehát a

P Q R S

téglalap ,,képe'' ugyancsak téglalap, melynek oldalai (

a'

és

b'

) általában különböznek az eredeti méretektől.
A két elrendezés (ugyanakkora be- és kivezetett áramok esetén) akkor egyenértékű, ha minden részletében ugyanakkora áramerősséget tartalmaz, vagyis

I' = I

. Ez láthatóan akkor teljesül, ha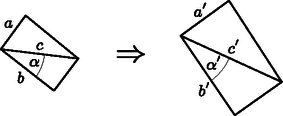

\begin{matrix} \frac{b'}{a'} = \frac{b}{a}, \end{matrix}

vagyis a transzformáció (kis méretek esetén) aránytartó. Ez a tulajdonság nemcsak az egymást derékszögben metsző rövid szakaszokra érvényes, hanem egy adott ponton átmenő, tetszőleges irányú, kicsiny szakaszpárokra is fennáll, ahogy azt a 2. ábra mutatja:

2. ábra

\begin{matrix} \frac{c'}{a'} = \frac{c}{a} . \end{matrix}

Az ábráról az is leolvasható, hogy a transzformáció szögtartó:

α' = α

.¹
Az arány- és szögtartó síkbeli transzformációkat konform leképezéseknek nevezik, és komplex változójú, komplex értékű, kellőképpen ,,sima'' (differenciálható) függvényekkel írhatók le. Ezek a leképezések a sík egy-egy (kicsiny) darabkáját csak odébbtolják, elforgatják és valamilyen arányban nagyítják (vagy kicsinyítik). Az eltolás, forgatás és nagyítás mértéke természetesen helyről helyre változhat, így az alakzat egésze lényegesen eltorzulhat, átalakulhat.
A továbbiakban bemutatunk néhány ‐ a fizikai alkalmazások szempontjából lényeges ‐ konform leképezést. Mivel az ilyen leképezések egymás után történő alkalmazása ugyancsak szög- és aránytartó transzformációt eredményez, néhány alapesetből kiindulva a fizikai problémák meglepően széles körének megoldására nyílik lehetőségünk.

1. Eltolás

Ha a sík egészét valamilyen adott (síkbeli) vektorral odébbtoljuk, ez a transzformáció nyilván arány- és szögtartó lesz, tehát konform leképezést valósít meg. A kapcsolat egy-egy pont régi és új koordinátái között:

\begin{matrix} x' = x + x_{0}, y' = y + y_{0}, \end{matrix}

ahol

x_{0}

és

y_{0}

állandók.

2. Nagyítás (kicsinyítés)

Egy másik szög- és aránytartó transzformáció képletei:

\begin{matrix} x' = λ x, y' = λ y, \end{matrix}

ahol

λ \neq 0

egy adott állandó. Ha

λ > 1

, a leképezés a síkbeli alakzatokat nagyítja,

λ < 1

esetben pedig kicsinyíti.

3. Forgatás

Kicsit bonyolultabb, de ugyancsak konform leképezés a sík pontjainak valamekkora

φ

szöggel történő elforgatása:

\begin{matrix} x' = x cos φ - y sin φ, y' = x sin φ + y cos φ . \end{matrix}

Az eddig felsorolt transzformációk lényegében nem változtatják meg az áramlási képet (az áramvonalakat), csupán annak felelnek meg, hogy a koordináta-rendszer kezdőpontját máshová helyezzük, a távolságok mértékegységét megváltoztatjuk (például centiméter helyett inch egységeket használunk), illetve az

x

tengelyt másfelé irányítjuk. A következő két leképezésnél azonban nem ez a helyzet, azok lényeges változást eredményeznek az árameloszlásban, tehát fizikailag különböző problémákat kapcsolnak össze.

4. ,,Legyező-leképezés''

Tekintsük azt a leképezést, ami az

y > 0

végtelen félsík egyes pontjaihoz tartozó helyvektor

x

tengellyel alkotott

φ

szögét megkétszerezi:

φ' = 2 φ

. Szemléletesen ez olyan, mintha egy legyezőt kétszeres méretre nyitnánk ki. A 3. ábrán egy

r

helyvektorú,

r

és

φ

polárkoordinátákkal megadott pont körüli, kicsiny

P Q R S

tartomány szögtartó transzformációját láthatjuk.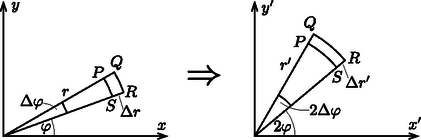

3. ábra

Ahhoz, hogy a leképezés (kicsi méretek esetén) aránytartó is legyen, az szükséges, hogy a

\begin{matrix} \frac{Δ r}{r \cdot Δ φ} = \frac{Δ r'}{r' \cdot 2 Δ φ} \end{matrix}

egyenlőség teljesüljön. Innen következik, hogy

\begin{matrix} r Δ r' - 2 r' Δ r = 0, \end{matrix}

vagyis (

Δ r ≪ r

és

Δ r' ≪ r'

esetén) fennáll, hogy

\begin{matrix} Δ (\frac{r^{2}}{r'}) = \frac{{(r + Δ r)}^{2}}{r' + Δ r'} - \frac{r^{2}}{r'} \approx \frac{r^{2} + 2 r Δ r}{r' + Δ r'} - \frac{r^{2}}{r'} \approx \frac{r}{r'^{2}} (2 r' Δ r - r Δ') = 0, \end{matrix}

amiből

\begin{matrix} \frac{r^{2}}{r'} = állandó \end{matrix}

következik. Látható, hogy a kétszeresére kinyitott ,,legyező'' esetében akkor kapunk szög- és aránytartó transzformációt, ha a kétszeres szög mellett a helyvektorok nagyságát négyzetre is emeljük és konstanssal megszorozzuk². Az állandó értéke tetszőleges lehet, de célszerű a nagyságát 1-nek választani.
A leképezés általánosítható a legyező tetszőleges arányú kinyitására. A fentebb leírtakhoz hasonlóan látható be, hogy

φ' = n φ

esetén a transzformáció akkor lesz aránytartó, ha

r' = r^{n}

, ahol

n

tetszőleges pozitív vagy negatív szám (

n \neq 0

).³

5. ,,Szalag-leképezés''

Véges szélességű, nagyon hosszú, elektromosan vezető lemezben folyó síkbeli árameloszlások leírásánál hasznos lehet egy olyan konform (szög- és aránytartó) leképezés, amely a szalagot egy végtelen síkba transzformálja. Legyen a szalag az

x

tengellyel párhuzamos és

y

irányban

2 π

széles. (Ha más lenne a szalag szélessége, alkalmas léptékű nagyítással mindig elérhető ez a kívánt méret.)
Válasszunk egy olyan transzformációt, ami az

x

tengellyel párhuzamos vonalakat (amelyekre

y = y_{0}

állandó,

0 < y_{0} < 2 π

) az origóból kiinduló ,,sugarasan'' szétfutó vonalakba viszi át. Ezeket a

φ' = állandó

összefüggés jellemzi, ahol

φ'

a leképezés során kapott vektoroknak az

x'

tengellyel bezárt szöge. Legyen például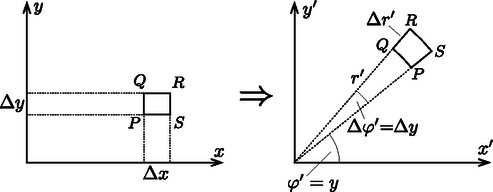

\begin{matrix} φ' = y . \end{matrix}

Ez a legegyszerűbb választás, ami teljesíti a fentebb leírt követelményeket. Az

x

tengellyel párhuzamos vonalseregre merőleges vonalak (egyenesek) egyenlete:

x = x_{0} = állandó

. Ezek az egyenesek a leképezés után az origón áthaladó ,,sugaras egyenesekre'' merőleges görbékbe, azaz valamekkora sugarú körökbe mennek át. Azt, hogy mi a kapcsolat az

x

koordináta és az

r'

sugár között, a leképezés aránytartóságának követelménye határozza meg.

4. ábra

A 4. ábráról leolvasható, hogy

\begin{matrix} \frac{Δ r'}{Δ x} = \frac{r' Δ φ'}{Δ y}, \end{matrix}

ahonnan

Δ φ' = Δ y

miatt

\begin{matrix} \frac{Δ r' (x)}{Δ x} = r' (x) . \end{matrix}

Ez az egyenlet (határesetben differenciálegyenlet) a kamatos kamat vagy a radioaktív bomlások exponenciális törvényével azonos alakú, emiatt a megoldása:

\begin{matrix} r' (x) = állandó \cdot e^{x} . \end{matrix}

Az állandó 1-nek választható, avagy egy egyszerű nyújtással 1-gyé tehető.⁴
A bemutatott arány- és szögtartó leképezések mindegyikének ,,inverze'' (visszafelé történő alkalmazása) is arány- és szögtartó, tehát azok is alkalmasak síkbeli vezetési (vagy áramlási) problémák leírására. Ugyancsak megengedett a konform leképezések egymást követő sorozatának alkalmazása. Bizonyos esetekben kihasználhatjuk még a probléma forgási és/vagy tükrözési szimmetriáját, amennyiben a vékony áramvezető lemez határvonalai is rendelkeznek ezekkel a szimmetriákkal. Mindezekre cikkünk II. (a KöMaL jövő havi számában megjelenő) részében mutatunk fizikai példákat, konkrét alkalmazásokat.

\begin{matrix} \begin{matrix} Elek Péter & Szász Krisztián \\ Debreceni Ref. Koll. & BME Fizikai Intézet, \\ Dóczy Gimn. 12. évf. & Budapest \end{matrix} \end{matrix}

¹A transzfomáció során az egyenes vonalak általában görbe vonalakba mennek át. Ilyen esetben a szögtartást úgy értjük, hogy egy ponton átmenő két görbe érintőjének egymással bezárt szöge a leképezés során nem változik.

²Megjegyzések: $(i)$ Az $x = y = 0$ pontban (vagyis a koordináta-rendszer origójában (a legyező ,,tengelyénél'') a transzformáció nyilván nem szögtartó. Ez a kivételes pont a transzformáció ,,szinguláris pontja''. $(i i)$ A leírt transzformáció a komplex számok nyelvén (az $x + i y = z$ és $x' + i y' = z'$ jelölés bevezetésével) így írható: $z' = állandó \cdot z^{2}$ .

³A komplex számok algebrájában jártasak felismerhetik, hogy az első három példában szereplő leképezés a $z' = z_{1} z + z_{0}$ lineáris függvénnyel ( $z_{0}$ és $z_{1}$ állandók), az általánosított ,,legyező-leképezés'' pedig a $z' = z^{n}$ komplex függvénnyel írható le.

⁴A komplex számok exponenciális alakját ismerők számára megjegyezzük, hogy a ,,szalag-leképezést'' a $z' = e^{z}$ komplex exponenciális függvény írja le.