| Cím: | Barangolás kockás papíron | ||
| Szerző(k): | Koncz Levente , Számadó László | ||
| Füzet: | 2018/szeptember, 326 - 334. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Cikkek, Másodfokú diofantikus egyenletek, Rácsgeometria | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Szeretjük, ha egy számsorozat általános tagja megadható képlettel. Például a páratlan számok, a páros számok, a háromszögszámok, a négyzetszámok előállítására gyorsan tudunk képletet adni. A számok megjelenítése egy-egy megfelelő figurával sokat segíthet a képlet előállításában. A figurális számokat régen egyforma kavicsokkal ábrázolták, ma kirakhatjuk őket például színes kupakokból. A ,,kockás papír'' négyzetrácsán is szemléltethetők ezek a számok. 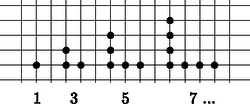 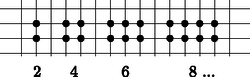 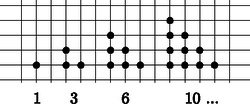 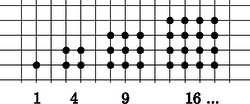 Milyen képlettel tudnánk megadni a következő számsorozat -edik tagját?
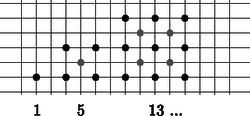 Az (1) sorozat számait látva érthetetlen lett volna, ha négyzetszámoknak nevezzük ezeket. Az ábrákat szemlélve viszont jogosnak érezhetnénk, de ez az elnevezés már foglalt. Mivel a négyzetszámok megszokott ábráján minden kis négyzetnek a közepét is bejelöltük, ezért ezeket a számokat középpontos négyzetszámoknak nevezi a szakirodalom. A középpontos négyzetszámok szemléltetésénél észrevehető az is, hogy egy pont van középen, és azt négyzet alakú pontrétegek veszik körül. Adott réteg minden oldala eggyel több pontot tartalmaz, mint a korábbi réteg. Ezt felhasználva bevezethetjük a középpontos sokszögszámok fogalmát is. Az ábrán példaként a középpontos hatszögszámok sorozatát szemléltetjük kockás papíron. 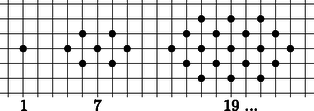 A (2) képlet eszünkbe juttathatja a Pitagorasz-tételt. Tekintsük azokat a derékszögű háromszögeket, amelyekben a két befogó hossza két egymást követő egész számmal adható meg: 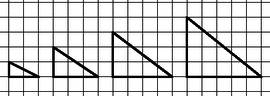 Az így kapott -edik derékszögű háromszög átfogójának hosszát az . középpontos négyzetszám négyzetgyöke adja: . Az ábrasorozat harmadik tagja a jól ismert 3, 4, 5 oldalhosszúságokkal megadott Pitagorasz-féle háromszög. Van-e még a sorozatban Pitagorasz-féle háromszög? A kérdésre az másodfokú diofantoszi egyenlet megoldása adja a választ. Ezekkel a kérdésekkel tanórán is foglalkoztunk, de az ilyen típusú egyenletek megoldása nem szerepel a középiskolai tananyagban, ezért függvénytáblázat, számológép, illetve számítógép segítségével próbáltak a diákjaink ilyen háromszögeket keresni. A függvénytáblázatban a -hoz megtaláljuk a Pitagorasz-féle számhármasokat. Ezek között csak egy további megfelelő van: 20, 21, 29. Grafikus számológéppel további számhármasokat is kaptunk. A számológép táblázatának első oszlopában az , a második oszlopában a értékeit írattuk ki. Így a -hez találtunk még két megfelelő háromszöget: 119, 120, 169, illetve 696, 697, 985. Óvatosan kell kezelnünk a számológép táblázatának számait. A számológép például a 288, 289, 408 számhármast is megadta, de ez nyilvánvalóan rossz, hiszen a utolsó számjegye 5, míg utolsó számjegye 4. A táblázat számait két tizedesre kerekítve a gép 408-nak vette a -et. Szondy Dániel számítógéppel a feltétel mellett összesen 11 számhármast talált: Ezeket egyszerű ''favágó'' módszerrel kereste, ezért kijelenthetjük, hogy eddig teljes a lista. Az ennél nagyobb számok keresése előtt egy érdekességet vett észre. Megfigyelte, hogy az első oszlopban a két egymás után következő szám hányadosa 5,83 körüli értéket vesz fel. Ezen érdekesség alapján elkészített egy új keresési algoritmust:
Vagyis az új derékszögű háromszög legkisebb oldalának hosszát Mi lehet az a titokzatos 5,83 körüli szám? A megtalált húsz derékszögű háromszög két befogója majdnem egyenlő hosszúságú. Minél nagyobb sorszámú háromszögeket nézünk a sorozatból, annál jobban az egyenlőszárú derékszögű háromszögeket juttatják az eszünkbe, amelyekben a befogó hosszának Az eddigi oldalhosszakat nézve rekurzív képletet is találtunk: Próbáltunk a Fibonacci-sorozathoz hasonló explicit képletet adni az
Ezek után utánanéztünk az interneten, hogy vajon mások is foglalkoztak-e már a MED háromszögekkel, s ha igen, akkor ők mire jutottak. Nem meglepő módon igen sok találatot kaptunk, a kérdésnek gazdag irodalma van. Sok érdekességre is bukkantunk, ezek közül ‐ a teljesség igénye nélkül ‐ itt csak néhányat említünk. Az [1]-ben például találunk egy bizonyítást arra, hogy végtelen sok ilyen háromszög van, és egy konstrukciót is kapunk ilyenek előállítására. Az azonban nem derül ki ebből a bizonyításból, hogy az így konstruálható háromszögeken kívül is vannak-e MED háromszögek. A [2]-ben találunk egy rövid bizonyítást arra nézve, hogy végtelen sok olyan háromszögszám van, amely egyben négyzetszám is. Könnyű ellenőrizni, hogy ha A [2] egyik állítása háromszögszám-négyzetszámok és a MED háromszögek közti szoros kapcsolatot is igazolja. Behelyettesítéssel ellenőrizhető, hogy az Végül [5] nem csak a majdnem egyenlőszárú derékszögű háromszögekkel, hanem a majdnem derékszögű, ezen belül a majdnem derékszögű egyenlőszárú háromszögekkel is foglalkozik, sőt a háromszögek e két osztálya között kapcsolatot is teremt. Egy háromszöget majdnem derékszögűnek nevezünk, ha oldalaira A kockás papíron a további barangoláshoz válasszuk a KöMaL 1989/10. számában megjelent Gyakorló feladatok egyetemi felvételire című összeállításból a következő feladatot: Nézzük röviden ennek a megoldását, de természetesen ezzel az elsőt is megoldjuk. Legyen
Az (5) és a (6) egyenletekből álló kétismeretlenes egyenletrendszer megoldásai adják a
A 12 osztói: 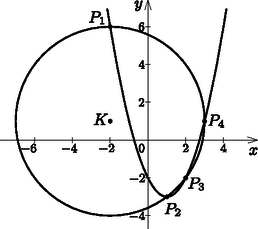 Szeretjük, ha a gyakorló feladatokat olyan szépre tervezik, hogy a megoldások egészek. Ebben az esetben is ez történt. Adott volt a rácson egy kör, amelynek a középpontja rácspont, sugarának hossza pedig egész. Adott volt továbbá az Van-e más elrendezés a fenti feltételek mellett? Ha van, keressünk ilyeneket. Ha elkezdünk rajzolgatni a kockás papíron, akkor hamar észrevehetjük, hogy speciális elrendezést érdemes keresnünk, mert ekkor gyorsan lehet sikerélményünk. Az origóban álló normálparabola rácspontjait bejelölve egymásra rakott húrtrapézokból álló torony jelenik meg előttünk. Az építmény egy egyenlő szárú derékszögű háromszöggel indul, ahogyan ezt az ábrán is láthatjuk. Bármely ilyen húrtrapéz köré írt köre és a normálparabola ezek szerint négy rácspontban metszi egymást. Vagyis végtelen sok olyan kört találtunk, amely a normálparabolát négy rácspontban metszi. Vajon ezeknek a köröknek hol van a középpontja? Van-e közöttük olyan, amelyiknek a sugara egész? 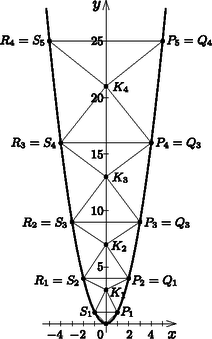 Az ábra alapján a Az Vizsgálataink alapján kiderült, hogy végtelen sok szimmetrikus ábra létezik, ahol a normálparabolát négy rácspontban metsz egy rácsközepű, egész sugárhosszúságú kör. A kockás papíron rajzolgatva szerettünk volna a 2. feladatban látott további, nem szimmetrikus elrendezést is találni. A véletlen keresgélés nem kecsegtetett nagy reményekkel. Elsőként Rátki Barnabás számítógép segítségével talált egy megfelelő új ábrát. Számolással ellenőrizhető, hogy az általa megadott Ebben az írásban ízelítőt szerettünk volna mutatni abból, hogy a füzetlapunk rácsa milyen sok érdekességet tartogat számunkra, milyen sok felfedezés várhat ránk, ha egy kicsit barangolunk a kockás papíron. Végezetül egy rövid feladatsorral szeretnék minden érdeklődőt biztatni erre a kalandozásra, újabb és újabb érdekes kérdések megfogalmazására. A figurális számokra vonatkozó bizonyításokat féltétlenül szemléltessük rácson is. A következő feladatok különböző nehézségűek, de reméljük, hogy mindenki talál kedvére valót. 1. Adjunk meg néhány háromszögszámot, amely négyzetszám is. 2. Milyen figurális számot és hányadikat kapjuk, ha az 3. Adjunk meg két egymást követő háromszögszámot, melyek különbsége kétjegyű négyzetszám. 4. Adjunk az 5. Igazoljuk, hogy a 2 6. Egy háromszögszámhoz adjuk hozzá valamelyik szomszédjának háromszorosát. Igazoljuk, hogy háromszögszámot kapunk. 7. Az első középpontos négyzetszám az 1. Adjuk meg a 77. középpontos négyzetszámot. 8. Igazoljuk, hogy minden középpontos négyzetszám páratlan. 9. Mutassuk meg, hogy ha a 10. Igazoljuk, hogy a középpontos négyzetszámok néggyel osztva egyet adnak maradékul. 11. Igazoljuk, hogy egy háromszögszám négyszereséhez 1-et adva középpontos négyzetszámot kapunk. 12. Adjuk meg az 13. Igazoljuk, hogy ha a 14. Igazoljuk, hogy ha az 15. Igazoljuk, hogy egy háromszögszám hatszorosához 1-et adva középpontos hatszögszámot kapunk. 16. Adjunk meg egy-egy olyan pitagoraszi számhármast, amelyben a legnagyobb szám (vagyis a derékszögű háromszög átfogójának hossza): 5, 13, 25, 41, 61, 85. 17. Bizonyítsuk be, hogy a másodiktól kezdve minden középpontos négyzetszám egy pitagoraszi számhármasban a legnagyobb tag. 18. Használjuk a cikk 3. feladatának jelöléseit. 19. Megadtunk a cikkben két nem szimmetrikus kör és parabola elrendezést a kívánt feltételek mellett. Van-e további ilyen elrendezés? 20. A cikkben szereplő 21. Illeszkedik-e végtelen sok rácspont az 22. Használjuk a cikk 3. feladatának jelöléseit. Adjuk meg
|