Kezdőlap


Cím:	Variációs elvek a klasszikus és a kvantumfizikában
Szerző(k):	Solt György
Füzet:	2018/december, 558 - 562. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Variációs elvek a klasszikus és a kvantumfizikában

A klasszikus fizika variációs elvei

Az írás I. része a klasszikus mechanika legkisebb hatás (Hamilton-) elvét és egyszerű alkalmazását mutatta be.¹ Az elv idővel a klasszikus fizika más területein (az elektrodinamikában, a relativisztikus mechanikában, a térelméletekben) is alkalmazásra talált, az

S

hatásfüggvényben szereplő Lagrange-függvény természetesen az adott témakörnek megfelelő dinamikai változókból (például elektromos és mágneses térerősségekből) épül fel. A hatáselvek erőssége, hogy a fizikai probléma megoldásának útját ,,egyetlen sorban'', az

S

hatásfüggvény felírásával kijelölik. Az elmélet (variációszámítást alkalmazó) részletes kifejtése ezután megadja azokat az összefüggéseket az

x_{i}

koordináták és a

v_{i}

sebességek között, melyek biztosítják az

\begin{matrix} S = \int L (x_{1}, v_{1} ...) d t \end{matrix}

függvény stacionárius értékét. Ezek az egyenletek (melyek a mechanikában a newtoni fizika egyenletei) már meghatározzák a keresett

x_{i} (t)

függvényeket.
De legkisebb hatást, legrövidebb utat vagy időt követelő intuitív variációs elvek már Euler (1744) és Lagrange (1760) variációszámítása előtt is voltak. A síktükrön való visszaverődés törvényét például Alexandriai Héron (i.sz. 10‐75) például a ,,legrövidebb út'' elvével indokolta [1].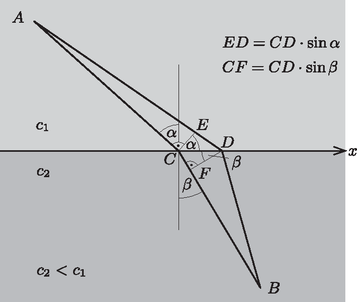

1. ábra. A Fermat-féle legrövidebb idő elvéből következik
a fénytörés Snellius‐Descartes-törvénye
(a részleteket lásd a cikk szövegében)

A legrövidebb idő elve

A modern kor első variációs elve, melyről a továbbiakban részletesebben lesz szó, P. Fermat (1601‐1665) francia matematikustól származik, akinek meggyőződése volt, hogy ,,a természet mindig a legrövidebb és legegyszerűbb utakat választja''. Utakon itt általánosan ,,utak-módok'' értendők, de a fényterjedés esetén Fermat valódi útra gondolt, amikor 1662-ben kimondta: ,,A fénysugár azt az utat választja, melynek befutásához a legrövidebb időre van szüksége.''
Az 1. ábrán látható elrendezésben a fény egy ,,optikailag ritka'' közeg

A

pontjából

c_{1}

sebességgel terjedve egy ,,optikailag sűrűbb'' közegbe hatol, ahol a sebessége

c_{2} < c_{1}

, így jut el a

B

pontba. A Fermat-elv szerint a határfelület

C

pontjának helyzetét (és ezzel az

α

beesési szöget, valamint a

β

törési szöget) az határozza meg, hogy az

A B

úton eltöltött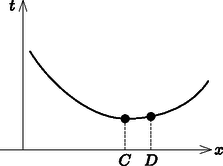

\begin{matrix} t = \frac{A C}{c_{1}} + \frac{C B}{c_{2}} \end{matrix}

idő minden más úthoz tartozó időhöz képest a legrövidebb (2. ábra). Fermat megmutatta, hogy

C

ilyen választásakor fennáll a

\begin{matrix} \frac{sin α}{sin β} = \frac{c_{1}}{c_{2}} \end{matrix}

összefüggés, ami éppen a Snellius‐Descartes-törvény, és ezzel megadta ennek a törvénynek első ‐ fizikailag helyes ‐ magyarázatát [1].

2. ábra. A fény terjedési ideje a határfelületen lévő fénytörési pont helyzetének függvényében

Megfordítva, a Snellius‐Descartes-törvényből következik, hogy a

t

idő a

C

pont helyzetének függvényében stacionárius (ahogy minimum esetén lennie kell). Ez azt jelenti, hogy egy

A C B

-hez nagyon közeli

A D B

úton a nagyon kicsi

C D

távolság első rendjében (első hatványával arányos mértékben) a

t

idő nem változik. Az

E D

szakasz ugyan

E D / c_{1}

többletidőt igényel, de a

C F

út kihagyásával nyert

C F / c_{2}

idő ezt éppen kompenzálja. Valóban, az 1. ábrán láthatóan

\begin{matrix} \frac{E D}{C F} = \frac{sin α}{sin β}, \end{matrix}

ezt

c_{2} / c_{1}

-gyel szorozva a Snellius‐Descartes-törvényből

E D / c_{1} = C F / c_{2}

következik. (Megfontolásunk során kihasználtuk, hogy kicsiny

C D

esetén

A C \approx A E

és

B F \approx B D

. A közelítés

C D

magasabb hatványainak elhanyagolása mellett jogos.)
Ha a fény

c

sebessége útszakaszonként változik, a teljes út befutásához szükséges

\begin{matrix} t = \sum \frac{Δ s_{i}}{c_{i}} \end{matrix}

idő, folytonosan változó

c

esetén pedig az

\begin{matrix} \int \frac{d s}{c} \end{matrix}

idő lesz minimális.

Miért működik a Fermat-elv?

A fény hullámtermészete fizikai magyarázatot ad a Fermat által megválaszolatlanul hagyott ,,hogyan'' kérdésre is, arra, hogyan találja meg a fénysugár

A

és

B

között a legrövidebb időre vezető

C

határpontot. Fermat még nem ismerhette a fényterjedés hullámelméletét, aminek első megfogalmazását C. Huygens (1629‐1695) holland fizikus, matematikus és csillagász írta le 1678-ban, és amelyet A-J. Fresnel (1788‐1827) francia fizikus fejlesztett tovább 1816-ban.
Az

A

-ból kiinduló fényhullámok (elektromágneses rezgések) valójában az egész határfelületre érkeznek és terjednek tovább

B

felé, de az úton eltöltött időtől függően különböző rezgési fázisban (ezáltal különböző amplitúdóval) jutnak el

B

-be. Mivel a

C

ponton átmenő sugár esetén a repülés idő stacionárius, a

C

közvetlen környezetéből

B

-be érkező hullámok fázisa (és amplitúdója) alig különbözik, ezek egymást erősítő konstruktív interferenciája nagy amplitúdót (ezáltal nagy intenzitást) eredményez. Ugyanakkor a

C

-től (több hullámhossznyival) távolabbi határpontokból jövő hullámok nagyon különböző fázisban érkeznek

B

-be, kioltják egymást, és

B

-ben csak a

C

-felől jövő fénysugár lesz látható.

Hatáselvek a mechanikában

A mechanikában az első minimumelvnek felfedezője, P. L. M. Maupertuis (1698‐1759) francia fizikus, matematikus, filozófus a ,,legkisebb hatás'' nevet adta (1744). Maupertuis szerint ,,ha a Természetben valami változás történik, a felhasznált hatás a lehető legkisebb marad''. Pontosabban: az anyagi pont, ha teljes energiája megmarad, olyan pályán mozog, hogy (a pálya egyes szakaszait

Δ s_{i}

-vel jelölve) az

m v

impulzus ,,hatása'', a

\begin{matrix} W = \sum m v_{i} Δ s_{i} \end{matrix}

összeg (

\int m v d s

integrál) értéke a lehető legkisebb marad. A pontos bizonyítás L. Eulerre maradt, aki megmutatta, hogy ez a feltétel valóban kijelöli a pálya (például a Nap gravitációs terében keringó bolygóknál az ellipszis) alakját. (A koordináták időfüggése azonban további számításokat igényel.)
Fermat és Maupertuis a minimumelveket intuitív módon a természet egyszerűségre törekvésével, tehát inkább ,,morális'', mint fizikai érveléssel indokolták. Fermat ezt elegendőnek érezte, de Maupertuis a ,,szép, egyszerű'' variációs elvekben metafizikai cél megvalósulását látta: ,,Ezek talán az egyedüli törvények, melyeket a dolgok teremtője alkotott, azért, hogy létrehozza látható világunk valamennyi jelenségét.'' Ugyanakkor a kortárs Lagrange a saját ,,modern'' legkisebb hatás elve és a newtoni mechanika ekvivalenciájának tudatában a tényeknél maradt: ,,Az elvet, melynek kissé pontatlanul a Legkisebb Hatás nevet adtam, nem tekintem metafizikai principiumnak, hanem a mechanika törvényeiből következő egyszerű és általános eredménynek.'' (A ,,pontatlanul'' arra utal, hogy a hatásfüggvény stacionárius, de nem feltétlenül minimális értékéről van szó.)

Pálya helyett kvantummechanikai valószínűség

Áttérve a kvantumfizikára, a mikrorészecskék a kvantummechanika jól ismert ,,határozatlansági relációja'' miatt nem jól meghatározott pályán mozognak, hiszen egy adott pillanatban a részecske

x (t)

helye csak bizonyos valószínűséggel ismerhető meg. A helykoordinátát és annak változását a hullámfüggvény, a

ψ (x, t)

(komplex) valószínűségi amplitúdó jellemzi, és

| ψ (x, t) |^{2}

adja meg annak valószínűségét (pontosabban valószínűségi sűrűségfüggvényét), hogy a

t

időpontban a mérés a részecskét az

x

helyen találja. A részecske mozgásakor a

ψ (x,0)

kezdeti (

t = 0

pillanatbeli) hullámfüggvény

t

idő alatt

ψ (x, t)

-re változik. A változás leírásához, tehát a

ψ

hullámfüggvény időfüggésének számításához az

A (0, x';