Kezdőlap


Cím:	Hány liter vizet kell a sivatagba vinni?
Szerző(k):	Csirmaz László
Füzet:	1982/november, 97 - 106. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az alábbi feladatot az 1980. évi Országos Középiskolai Tanulmányi Verseny II. fordulóján a matematika II. tagozatú osztályok számára tűzték ki:
Egy sivatagi expedíciónak a sivatag szélén levő táborból egy liter vizet kell eljuttatnia a sivatagnak olyan pontjára, amely $n$ napi járásra van az expedíció táborától. A szállítást úgy kell megszervezni, hogy
a) az expedíció tagjai sohasem vihetnek magukkal fejenként 3 liternél több ivóvizet;
b) a sivatagban töltött minden nap folyamán az expedíció valamennyi tagjának meg kell innia egy‐egy liter vizet;
c) feladatuk teljesítése után az expedíció valamennyi tagjának vissza kell térnie a táborba.
Legalább hány liter ivóvíznek kell lennie a táborban, hogy teljesíthet legyen a kitűzött feladat?
Ebben a cikkben a feladat megoldásairól lesz szó. Azért beszélünk megoldásokról és nem a megoldásról, mert a szövegből nem derül ki pontosan, hogy mik is azok a feltételek, amelyek mellett a sivatagba az egy liter vizet el kell juttatni. A különböző lehetséges értelmezések különböző végeredményekhez vezetnek, a megoldandó feladat nehézsége is más‐más. A verseny résztvevői között nem akadt olyan, aki a feladat szövegéhez talán legszorosabban kapcsolódó ‐ általunk harmadikként tárgyalandó ‐változatot oldotta volna meg. A második változat egy dolgozatban szerepelt, míg a döntő többség véleménye szerint a feladatot úgy kell értelmezni, ahogyan az az első változatban szerepel.
Mielőtt a feladat megoldásához érdemben hozzálátnánk, néhány megjegyzést teszünk. Először is feltesszük, hogy azok, akik egész nap a táborban maradnak, nem isznak vizet, vagy legalábbis az általuk elfogyasztott vízmennyiség nem tartozik a meghatározandó készlethez. Másodszor, feltehetjük, hogy az expedíció tagjai a sivatagban csak a célt a táborral összekötő szakasz mentén mozognak, továbbá ‐ mivel ezt egyik feltétel sem tiltja ‐ útjuk mentén tetszőleges helyen tetszőleges mennyiségű vizet felhalmozhatnak
A b) feltétel szerint az expedíció tagjai minden a sivatagban töltött nap folyamán egy liter vizet isznak meg. Az azonban nem derül ki, hogy azoknak is jár-e az 1 liter víz, akik nem egész napot töltenek a sivatagban. Feltesszük, hogy igen, vagyis a b) feltételt a következő feltétellel helyettesítjük:
b') a sivatagban töltött minden megkezdett napra az expedíció tagjainak jár egy-egy liter víz.
Végül feltesszük azt is, hogy az expedíciónak elég sok tagja van, vagyis ha új embert kell bevetnünk, akkor mindig akad pihent tartalék.

Első változat

Bemelegítésként vizsgáljuk meg, hogyan tudják az expedíció tagjai a kitűzött feladatot megoldani

n

kis értékei mellett.

n = 1

esetén 1 nap járóföldre kell 1 liter vizet eljuttatnunk. Ehhez elég 1 ember és 3 liter víz: az ember reggel elindul a 3 liter vízzel a kulacsában; délben megiszik 1 litert, este megérkezik a célhoz. Ott leteszi a nála levő 2 liter víz felét. Másnap visszaindul, útközben megissza a kulacsban maradt 1 litert, estére visszaérkezik a táborba. Ezzel a feladatot megoldotta, s nyilván ehhez 3 liternél kevesebb víz nem elég.
Legyen most

n = 2

. Világos, hogy a célhoz csak egy ember megy el ‐ a szükséges 1 liter vizet egyedül is el tudja vinni. Ez pedig azt jelenti, hogy a tábortól

(P_{0})

egy napi járóföldre levő pontból

(P_{1})

teli kulaccsal ‐ 3 liter vízzel ‐ kell elindulnia a cél

(P_{2})

felé (1. ábra). Azonban még ha a táborból teli kulaccsal indult is, útközben 1 litert megivott! A hiányt

P_{1}

-ben pótolnia kell. Másrészt mikor

P_{2}

-ből jövet visszaérkezik

P_{1}

-be, kulacsa egészen üres, s hogy szomjan ne haljon

P_{1}

és a tábor között,

P_{1}

-ben újabb liter víznek kell várnia. Így

P_{1}

-be még két liter vizet kell eljuttatnunk. Ehhez

P_{0}

-ból két embert kell indítanunk (nem feltétlenül egyszerre) tele kulaccsal.

P_{1}

-ig megisznak 1‐1 litert, ott letesznek 1‐1 litert, s visszamennek a táborba a megmaradt 1‐1 liter vizükkel.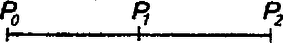

1. ábra

Összesen három kulacsot kellett tele töltenünk, vagyis a felhasznált vízmennyiség

3 \cdot 3 = 9

liter.
Ha

n = 3

, akkor az előzőhöz hasonlóan 2 l vizet kell eljuttatnunk az 1 napi járóföldre levő

P_{1}

pontba, s 2 litert

P_{2}

-be is. Ha ez már megtörtént, akkor az expedíció egy tagja induljon el a táborból tele kulaccsal. Mire

P_{1}

-be ér, kulacsából 1 liter hiányozni fog, de ezt a

P_{1}

-ben található 2 liter vízből pótolja. Most továbbindul

P_{2}

-be, ott ismét pótolja a

P_{1}

és

P_{2}

között elfogyasztott vizet.

P_{2}

-ből teli kulaccsal indul a cél,

P_{3}

felé. Ott letesz 1 litert, mire visszaérkezik

P_{2}

-be minden vize elfogyott. A

P_{2}

-ben maradt 1 liter vízzel visszamegy

P_{1}

-be, az ottani vízzel pedig szerencsésen visszaérkezik a táborba.
Nézzük ehhez mennyi vízre van szükség !

P_{2}

-be 1 liter vizet ‐ az előzőek szerint ‐ 9 literből,

P_{1}

-be pedig 3 literből tudunk eljuttatni, így kell

3 + 2 \cdot 3 + 2 \cdot 9 = 27

liter.
Azt sejthetjük, hogy ha a táborban

3^{n}

liter víz van, akkor a feltételeknek megfelelően 1 litert el tudunk juttatni

n

napi járóföldre. Láttuk, hogy ez

n = 1,2,3

esetében valóban így is van, s tegyük fel, hogy

n = 1,2, ..., k - 1

mellett ezt már beláttuk.

k

napi járóföldre 1 liter vizet ‐ az előbbiekkel analóg módon ‐ úgy juttathatunk el, hogy először egy napi, 2 napi,

...

(k - 1)

napi járóföldre 2‐2 litert vitetünk (ehhez a táborban

2 \cdot 3 + 2 \cdot 3^{2} + ... + 2 \cdot 3^{k - 1}

literre van szükség). Ezután egyetlen ember teli kulaccsal nekivág a sivatagnak. Minden nap végén pótolni tudja az aznap elfogyasztott vízmennyiséget egészen a

(k - 1)

-edik nap végéig, onnan elvisz 1 litert a

k

napi járóföldre levő pontba, majd visszafelé is minden nap este megtalálja a következő napra szükséges 1 literét. A felhasznált vízmennyiség

\begin{matrix} 3 + 2 \cdot 3 + 2 \cdot 3^{2} + ... + 2 \cdot 3^{k - 1} = 1 + (3 - 1) (1 + 3 + 3^{2} + ... + 3^{k - 1}) = 3^{k} \end{matrix}

liter, tehát az állítás

n = k

mellett is igaz. A teljes indukció elve alapján a sejtésünket ‐ vagyis, hogy

3^{n}

liter víz elegendő ahhoz, hogy

n

napi járóföldre 1 liter vizet eljuttassunk ‐ bizonyítottuk.
Az eljárást követve a

3^{n}

literből a

P_{1}

pontba összesen

3^{n - 1}

liter jut el, a

P_{2}

-be

3^{n - 2}

liter, általában az

i

napi járóföldre levő

P_{i}

pontba

3^{n - i}

liter. Az is könnyen látható, hogy

P_{i - 1}

és

P_{i}

között az expedíciónak összesen

2 \cdot 3^{n - i}

tagja fordult meg (mindenkit annyiszor számítva, ahányszor belépett ebbe az intervallumba), mégpedig ezek fele

P_{i - 1}

-ből

P_{i}

-be, a másik fele

P_{i}

-ből

P_{i - 1}

felé tartott.
Az expedíció tagjainak indulását úgy is megszervezhetjük, hogy egyáltalán ne kelljen vizet tárolni a sivatagban. A 2. ábrán egy ilyen ütemezést mutatunk be

n = 3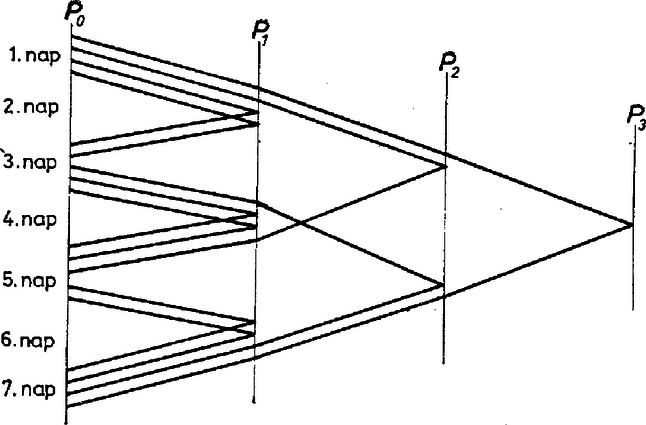

-ra.

2. ábra

Azt is sejthetjük, hogy ez a

3^{n}

liter víz nemcsak elegendő a feladat végrehajtásához, hanem szükséges is: hogyan is tudnánk megtakarítani akár egy cseppet is? Vannak sejtések, melyek igazak, s vannak melyek nem. Sajnos ez a sejtésünk az utóbbi csoportba tartozik: már

n = 2

esetén sincs szükség 9 literre. A feladat 6 liter vízből is megoldható például a következő módon (3. ábra).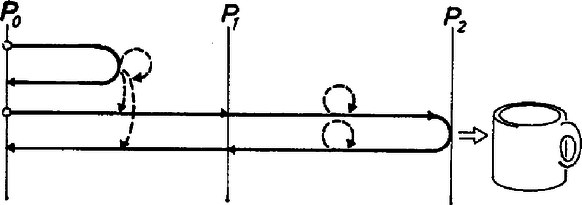

3. ábra

Az expedíció egyik tagja induljon el egy teli kulaccsal. Fél napi járóföldre a tábortól igyon meg egy liter vizet. A kulacsot a megmaradt két literrel tegye le, és menjen vissza a táborba. Összesen egy napot töltött a sivatagban, s az erre az időre járó 1 liter vizet el is fogyasztotta. Fél napi menetelés után abból a kulacsból, amit kollégája az előző nap ott hagyott, megiszik 1 liter vizet, s továbbmegy. Estére az egy napi járóföldre levő

P_{1}

pontba jut. Innen másnap reggel 3 liter vízzel indul tovább

P_{2}

-be, ott letesz 1 litert, s üres kulaccsal érkezik vissza

P_{1}

-be. A tábor és

P_{1}

között félúton még egy liter víz vár rá, így emberünk baj nélkül jut vissza a táborba.
A 3 liter víz megtakarítását az tette lehetővé, hogy az expedíció első tagja fél napi járóföld után fordult vissza. Bár első pillanatban úgy érezzük, ezt nem teheti meg, a feltételeket újra végigolvasva láthatjuk, hogy azok ezt nem tiltják. Ennek ellenére a legtöbb megoldó úgy érezte, hogy a következő megszorítás lappangva ott bújkál a feladat szövegében:
d) az expedíció tagjai napközben nem állhatnak meg és nem fordulhatnak vissza,

és természetesen mindenki ugyanakkora utat tesz meg egy nap alatt. Megmutatjuk, két különböző módon is, hogy e feltétel mellett a

3^{n}

liter vízre szükség is van.
Tegyük fel tehát, hogy az a)‐d) feltételek mellett sikerült az expedíció tagjainak a feladatukat végrehajtani. Jelöljük a tábortól

i

napi járóföldre levő pontot

P_{i}

-vel

(0 ≦ i ≦ n)

, a

P_{i}

pontba vagy azon túl eljutó vízmennyiségét

v_{i}

-vel, és

x_{i}

-vel az expedíció azon tagjainak számát, akik

P_{i - 1}

-ből

P_{i}

felé elindultak, mindenkit annyiszor számolva, ahányszor

P_{i - 1}

-et elhagyta. A d) feltétel szerint ezek mindegyike eljutott

P_{i}

-be, s mivel mindenkinek végül vissza kell jutnia a táborba, azért

P_{i}

-ből vissza

P_{i - 1}

-be is pontosan

x_{i}

tagja ment az expedíciónak.
Az

x_{i}

mennyiség definíciójában azért kellett ilyen óvatosan fogalmaznunk, mert az expedíció bármely tagja ,,ingázhat" a

P_{i}

pontok között, s ugyanazt a

P_{i - 1} P_{i}

utat sokszor megteheti.
Ha a szállítást az expedíció tagjai úgy szervezik, ahogyan azt korábban leírtuk, akkor

v_{i} = 3^{n - i}

(hiszen

P_{i}

-be összesen ennyi víz jut el) és

x_{i} = 3^{n - i}

.
Tudjuk, hogy mindegyik

x_{i}

nem-negatív,

v_{n} ≧ 1

(ez a feladat), és azt szeretnénk megmutatni, hogy

v_{0} ≧ 3^{n}

. Nézzük, mit tudunk!

P_{i - 1}

-ből

P_{i}

felé összesen

x_{i}

alkalommal indultak el, visszafelé is ugyanennyien jöttek, tehát a két pont között

2 x_{i}

liter víz fogyott el (4. ábra).

4. ábra

Ezt a

2 x_{i}

litert, továbbá azt a

v_{i}

litert, amelynek

P_{i}

-be kell jutnia, az

x_{i}

darab,

P_{i - 1}

-ből

P_{i}

-be tartó út alkalmával el kell tudni szállítani

P_{i - 1}

-ből. Tehát egyrészt

\begin{matrix} 3 x_{i} ≧ 2 x_{i} + v_{i}, (1 ≦ i ≦ n) \end{matrix}

(1)

másrészt

\begin{matrix} v_{i - 1} ≧ 2 x_{i} + v_{i} (1 ≦ i ≦ n) \end{matrix}

(2)

hiszen legalább

2 x_{i} + v_{i}

liter víznek el kell hagynia a

P_{i - 1}

pontot.
A

v_{n} ≧ 1

feltétel alapján (

n

napi járóföldre legalább 1 liter vizet kell eljuttatni), (1)-ből

x_{n} ≧ v_{n} ≧ 1

adódik majd (2)-ből

v_{n - 1} ≧ 2 + 1 = 3

. Ismét (1)-ből

x_{n - 1} ≧ v_{n - 1} ≧ 3

, (2)-ből pedig

v_{n - 2} ≧ 2 \cdot 3 + 3 = 9

. Hasonlóan továbbmenve végül is azt kapjuk, hogy

v_{0} ≧ 3^{n}

, ahogyan kívántuk.
A másik bizonyítás alapötlete a következő. A vizet a sivatag egy távolabbi pontjára nehezebb bevinni, mint egy közelebbire, ezért ott a víz étékesebb. Mondjuk 1 liter víznek az értéke a táborban

h_{0} = 1

, a tábortól

i

napi járóföldre peg

h_{i}

. Ha a

h_{i}

számokat ügyesen választjuk, akkor elérhetjük, hogy az expedíció tevékenysége folyamán a még meglevő, a sivatagban és a táborban valahogyan szétosztott víz összértéke ne nőjön. S ha még ezt úgy is meg tudjuk csinálni, hogy

h_{n} = 3^{n}

legyen, akkor készen vagyunk : az expedíció tevékenységének befejezésekor a víz értéke legalább

3^{n}

(hiszen van 1 liter,

3^{n}

értékű víz

n

napi járóföldre), ezért kezdetben is legalább ilyen értékű víznek kellett a táborban lennie. Ám a táborban 1 liter víz értéke csak 1, azért ez éppen

3^{n}

liter vizet jelent.
Az ötlet kivitelezéséhez még egy észrevételre van szükségünk. Ha az expedíció egy tagja a sivatagban tartózkodik, akkor ezzel csökkenti az ott található víz értékét, hiszen ebből a vízből kell fedezni a táborba való visszajutáshoz szükséges mennyiséget.
Ezek után lássuk az értékelést. Tegyük fel, hogy vége van egy napnak, vagyis az expedíció minden tagja valamelyik

P_{i}

pontban (

i

egész,

0 ≦ i ≦ n)

tartózkodik. Jelölje

e_{i}

P_{i}

-ben tartózkodó emberek számát,

v_{i}

pedig azt, hogy

P_{i}

-ben, valamint

P_{i - 1}

és

P_{i}

között együttvéve hány liter víz van. Ehhez az állapothoz a következő értéket rendeljük:

\begin{matrix} É = (v_{o} - \frac{3}{2} e_{0}) + 3 (v_{1} - \frac{3}{2} e_{1}) + ... + 3^{i} (v_{i} - \frac{3}{2} e_{i}) + ... + 3^{n} (v_{n} - \frac{3}{2} e_{n}) . \end{matrix}

(3)

Állítjuk, hogy ez az érték nem nő. Ebből már következik, hogy az expedíció feladatának végrehajtásához legalább

3^{n}

liter vízre szükség van. Kezdetben ugyanis

v_{0}^{k e z d}

és

e_{0}^{k e z d}

kivételével az összes többi

v_{i}^{k e z d}

és

e_{i}^{k e z d}

érték 0. A feladat végrehajtása után

e_{0}^{v é g}

kivételével az összes

e_{i}^{v é g}

értéke 0 ‐ ez jelenti azt, hogy mindenki visszatért a táborba ‐, és ezért

e_{0}^{v é g} = e_{0}^{k e z d}

, továbbá

v_{n}^{v é g} ≧ 1

és

v_{i}^{v é g} \geq 0

minden

0 ≦ i ≦ n

-re. A (3) által definiált érték nem nőtt, ezért

\begin{matrix} 3^{n} - \frac{3}{2} e_{0}^{v é g} ≦ É^{v é g} ≦ É^{k e z d} ≦ v_{0}^{k e z d} - \frac{3}{2} e_{0}^{k e z d}, \end{matrix}

amiből valóban következik, hogy

3^{n} ≦ v_{0}^{k e z d}

. Így csak azt kell megmutatnunk, hogy (3) értéke nem nő. Ehhez pedig elegendő ellenőrizni, hogy az a változás, amit egyetlen ember okoz, nem lehet pozitív, hiszen az összes változás az emberek által okozott változások összege.
Legyen az expedíciónak az általunk vizsgált tagja a

P_{i}

pontnál. Három dolgot csinálhat:

P_{i}

-ben marad, előremegy

P_{i + 1}

-be, vagy pedig visszafelé

P_{i - 1}

-be. Az első esetben

P_{i}

-ben 1 liter vizet megiszik, azaz

v_{i}

-t eggyel csökkenti, a változás

(- 3^{i})

, negatív. A második esetben

x

liter vizzel a kulacsában

(1 \leq x \leq 3)

P_{i + 1}

-be indul, akkor

v_{i}

-t

x

-szel,

e_{i}

-t eggyel csökkentette,

v_{i + 1}

-et

(x - 1)

-gyel,

e_{i + 1}

-et pedig eggyel növelte. A változás:

\begin{matrix} - 3^{i} (x - \frac{3}{2}) + 3^{i + 1} (x - 1 - \frac{3}{2}) = 3^{i} (2 x - 6) ≦ 0. \end{matrix}

Végül a harmadik esetben, ha

P_{i - 1}

-be

x

liter vízzel indul (és

x - 1

literrel érkezik), akkor a változás

\begin{matrix} 3^{i - 1} (x - 1 - \frac{3}{2}) - 3^{i} (x - \frac{3}{2}) = 3^{i - 1} (2 - 2 x) ≦ 0. \end{matrix}

Ezzel az állítást beláttuk.
Második változat
Láttuk, hogy 2 napi járóföldre 1 liter vizet 6 literből lehet eljuttatni. Ezt ennél kevesebbel már nem lehet megtenni. Ugyanis az, aki a vizet a célba juttatja, megiszik 4 litert (kettőt oda, kettőt vissza), és 1 litert letesz a sivatagban. Ezt az 5 litert egyetlen ember használja fel, de egyetlen alkalommal legfeljebb 3 litert tud magával vinni. Ezért vagy visszafordul a többi vízért ‐ de akkor 4 napnál tovább tartózkodik a sivatagban, és legalább 5 liter víz jár neki ‐ vagy valaki beviszi a sivatagba a további 2 litert ‐, de ekkor ennek az embernek jár még további 1 liter víz.
Nézzük meg mi történik, ha a d) feltétel helyett olyan feltételt teszünk, amely megengedi, hoyg az expedíció tagjai fél nap elteltével is visszaforduljanak :

d^{*})

az expedíció tagjai napközben nem állhatnak meg, és visszafordulni is csak fél nap elteltével lehet.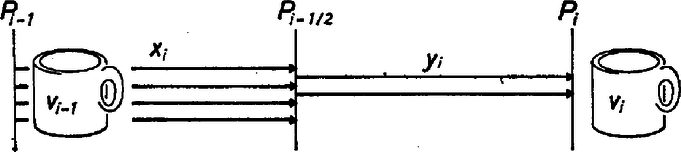

5. ábra

d^{*})

feltétel biztosítja azt is, hogy a nap végére mindenki egész napi járásra legyen a tábortól. Az ebben az esetben is szükséges vízmennyiséget az első megoldásban használtakhoz hasonlóan határozzuk meg. Ennek érdekében tegyük fel, hogy az expedíció sikeresen végrehajtotta a feladatát úgy, hogy a

d^{*})

feltétel is teljesült. Jelölje most is

P_{i}

a tábortól

i

napi járóföldre levő pontot, és

v_{i}

azt a vízmennyiséget, ami

P_{i}

-be vagy azon túl eljutott. Legyen

x_{i}

azoknak a száma, akik

P_{i - 1}

-től

P_{i - \frac{1}{2}}

-ig mentek (mindenkit annyiszor számítva, ahányszor ezt az utat megtette),

y_{i}

pedig azoké, akik től

P_{i - \frac{1}{2}}

-ből

P_{i}

-be mentek (5. ábra). Az első utat persze csak délelőtt, a másodikat csak délután tehették meg. Természetesen

P_{i - \frac{1}{2}}

-től vissza

P_{i - 1}

-be is

x_{i}

ember ment,

P_{i}

-től

P_{i - \frac{1}{2}}

-ig pedig

y_{i}

. Ez összesen

2 x_{i} + 2 y_{i}

félnapos utat jelent, tehát az expedíció tagjai

P_{i - 1}

és

P_{i}

között legalább

x_{i} + y_{i}

teljes napot töltöttek. Így ezen az útszakaszon legalább

x_{i} + y_{i}

liter víz fogyott el. Ezt és a

P_{i}

-be eljutott

v_{i}

liter vizet

P_{i - 1}

-ből el kellett hozni, tehát az alábbi egyenlőtlenségeknek fenn kell állniuk:

\begin{matrix} 3 x_{i} ≧ x_{i} + y_{i} + v_{i}, \end{matrix}

(4)

\begin{matrix} v_{i - 1} ≧ x_{i} + y_{i} + v_{i} . \end{matrix}

(5)

Másrészt

P_{i}

-be összesen

y_{i}

ember jutott el, és ezek vitték a

v_{i}

liter vizet

P_{i}

-be:

\begin{matrix} 3 y_{i} ≧ v_{i} . \end{matrix}

(6)

A (4)‐6) összefüggések és

v_{n} ≧ 1

segítségével könnyen tudunk alsó korlátot mondani

x_{i}, y_{i}, v_{i}

-re. (6) alapján

y_{n} ≧ 1

, (4)-ből

x_{n} ≧ 1

, (5)-ből pedig

v_{n - 1} ≧ 3

. Ismét (6) szerint

y_{n - 1} ≧ 1

, majd (4)-ből és (5)-ből

x_{n - 1} ≧ 2

és

v_{n - 2} ≧ 6

. Általában

v_{n - i} ≧ 3 \cdot 2^{i - 1}, y_{n - i} ≧ 2^{i - 1}, x_{n - i} ≧ 2^{i}

(ezt például

i

-re vonatkozó indukcióval igazolhatjuk), ezért

v_{0} ≧ 3 \cdot 2^{n - 1}

. Összefoglalva, a táborban eredetileg legalább

3 \cdot 2^{n - 1}

liter víz volt.
Annak meggondolását, hogy ennyi vízzel a feladat a

d^{*})

feltétel betartása mellett végre is hajtható, az olvasóra bízzuk. A 6. ábrán azt mutatjuk be, hogyan lehet

12 = 3 \cdot 2^{2}

liter vízzel három napi járóföldre 1 liter vizet eljuttatni. A körökből induló nyilak az expedíció tagjainak útját jelzik, a szaggatott nyilak pedig azt, hogy ki és hol itta meg a szállított vizet.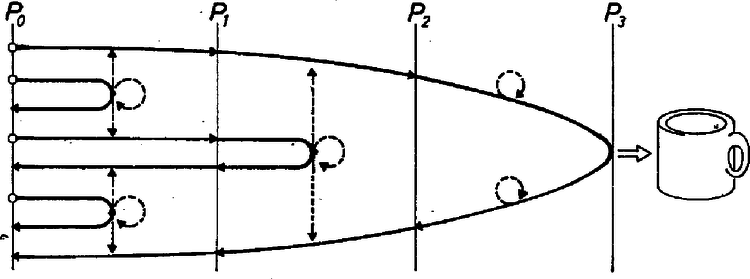

6. ábra

Harmadik változat
Ahhoz, hogy három napi járóföldre egy liter vizet az első változat szerint eljuttassunk, a táborban

3^{3} = 27

literre van szükség. Ha a második szerint akarjuk ezt megtenni,

3 \cdot 2^{2} = 12

liter is elég. Lehet-e ezt a vízmennyiséget még lejjebb szorítani? Bizony lehet: A feladat elvégzéséhez 10 liter is elég: Az expedíció munkáját például a következőképpen szervezhetjük (7. ábra). Az egyik (és feltehető, hogy egyetlen) tag az első nap háromszor fordul, és összesen 9 liter vizet

1 / 5

napi járóföldre bevisz a sivatagba, a tizedik litert valamikor napközben a táborban megissza. Az első nap végén 9 liter vízzel a sivatagban éjszakázik,

1 / 5

napi járóföldre a tábortól. A második nap ismét háromszor fordul, s második éjszakáját 8 liter víz társaságában a tábortól

2 / 5

napi járóföldre tölti. Ebből a nyolc literből egyet itthagy, egyet a harmadik nap folyamán megiszik, s 6 litert ‐ kétszer fordulva ‐ további

1 / 3

napi járófölddel beljebb visz.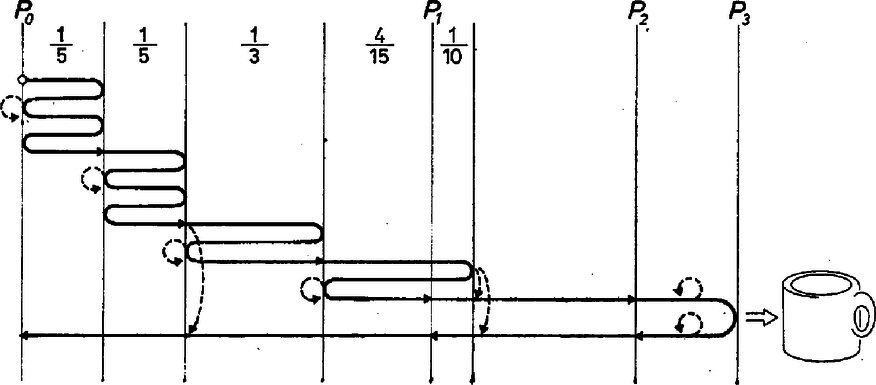

7. ábra

Ezzel a

P_{1}

pontot

1 - 1 / 5 - 1 / 5 - 1 / 3 = 4 / 15

napi járóföld távolságra megközelítette. Negyedik nap a 6 literből kettőt innen további

4 / 15 + 1 / 10

távolságra visz és azt ott leteszi, majd visszamegy a sivatagban hagyott 4 liter vízhez, abból egyet megiszik, a megmaradt 3 literrel éppen

P_{1}

-be jut, hiszen

3 \cdot 4 / 15 + 2 \cdot 1 / 10 = 1

.
Nézzük, hogy az ötödik nap reggelén mi a helyzet. Emberünk tele kulaccsal egy napi járóföldre van.

P_{0}

és

P_{1}

között a sivatagban (

P_{0}

-tól

2 / 5

napi járóföldre) egy liter,

P_{1}

és

P_{2}

között (

P_{1}

-től

1 / 10

napi járóföldre) két liter víz van. Minden el van rendezve tehát, bátran nekivághat a célhoz vezető útnak.

P_{1}

és

P_{2}

között odaúton az egyik, visszaúton a másik liter vizet issza meg,

P_{2}

és

P_{3}

között kulacsának tartalmára támaszkodhat, végül

P_{1}

-ből visszafelé a táborba szintén megtalálja az aznapra szükséges 1 liter vizet.
Azt, hogy ennél kevesebb víz nem elegendő, nem bizonyítjuk. Viszont megmutatjuk, hogy legalább

{(5 / 3)}^{n}

liter víznek lennie kell a táborban ahhoz, hogy az expedíció tagjai

n

napi járóföldre be tudjanak vinni 1 liter vizet az a), b'), c) feltételek mellett.
A bizonyítás módszeréűl a már bemutatott ,,értékelési eljárást" választjuk. Ha egy nap végén a tábortól

x

napi járóföldre

v_{x}

liter víz van, legyen annak értéke

v_{x} \cdot {(5 / 3)}^{x}

; ha ott az expedíció egy tagja tartózkodna, annak értéke

- (3 / 2) \cdot {(5 / 3)}^{x}

. A fenti állítás azonnal következik abból, hogy estéről estére az összes vízmennyiségnek és az embereknek az értékét összeadva, ez az összeg nem nőhet ‐ ezt pontosan úgy láthatjuk be, mint az első változatban tettük. Azt pedig, hogy az összérték nem nőhet, úgy bizonyítjuk, hogy megmutatjuk: az expedíció bármely tagja által egy nap alatt okozott változás nem pozitív. A teljes változás ugyanis az egyes tagok által okozott változások összege.
Nézzük tehát az expedíció egy tagjának egy napi útját.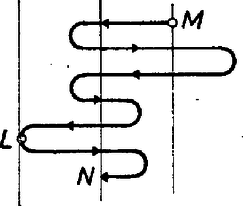

8. ábra

Valamilyen

M

pontból indul, ide-oda ingázik, s végül egy

N

pontba jut el. A megtett út legfeljebb egy napi járóföld. A nap folyamán megiszik összesen 1 liter vizet, s ennek értéke legalább annyi, mintha ezt útjának a táborhoz legközelebbi pontjában (

L

) fogyasztaná el. Útja során szállíthatott vizet ‐ természetesen minden pillanatban legfeljebb 3 litert ‐, s ezzel a tevékenységével akkor növeli legjobban a víz összértékét, ha a tábor felé üres kulaccsal megy, a tábortól távolodva pedig maximális mennyiséget visz magával.
Feltehetjük még azt is, hogy a pálya nem tartalmaz két, a sivatag felé záródó ,,hurkot" (9. ábra).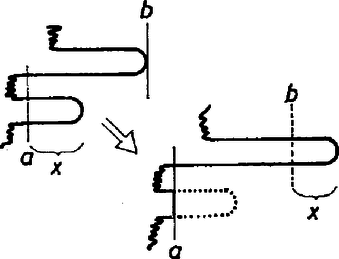

9. ábra

Vágjuk le ugyanis azt, amelyik a táborhoz közelebb kezdődik, és illesszük a másik végére. Ezzel a megteendő út nem változik, ugyanakkor a hurok eredeti helyén ‐ mondjuk

a

-tól

(a + x)

-ig ‐ szállított víz értéke

3 \cdot {(5 / 3)}^{a}

-ról

3 \cdot {(5 / 3)}^{a + x}

-re nőtt, vagyis a változás

3 \cdot {(5 / 3)}^{a} \cdot ({(5 / 3)}^{x} - 1)

, míg a hurok új helyén

b

-től

(b + x)

-ig lehet 3 liter vizet szállítani, s a változás

3 \cdot {(5 / 3)}^{b} \cdot ({(5 / 3)}^{x} - 1)

, ami

b > a

miatt több, mint korábban.
A 10. ábrán azt mutatjuk be, hogy a hurkok ismételt ,,levágásával" végül is milyen útvonalhoz jutunk: az

M

pontból előremegyünk a

K

pontig, onnan vissza az

L

-ig és

L

-ből előre az

N

végpontig.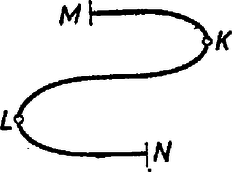

10. ábra

Jelöljük ezeknek a pontoknak a tábortól mért távolságát (napi járóföldben kifejezve) a megfelelő kisbetűkkel. Az összes megtett út legfeljebb 1, tehát

\begin{matrix} (k - m) + (k - l) + (n - l) ≦ 1, k ≧ m, k ≧ l, n ≧ l . \end{matrix}

(7)

Az útvonalnak a táborhoz legközelebbi pontja

M

vagy

L

, így az emberünk által napközben elfogyasztott víz értéke legalább

{(5 / 3)}^{m i n (l, m)}

. Így a megváltozás legfeljebb

\begin{matrix} [\frac{3}{2} {(\frac{5}{3})}^{m} - \frac{3}{2} {(\frac{5}{3})}^{n}] + [3 {(\frac{5}{3})}^{k} - 3 {(\frac{5}{3})}^{m}] + [3 {(\frac{5}{3})}^{n} - 3 {(\frac{5}{3})}^{l}] - {(\frac{5}{3})}^{m i n (l, m)} . \end{matrix}

Az első tag azt fejezi ki, hogy emberünk az

M

pontból az

N

-be került; a második azt, hogy

M

-ből 3 liter vizet

K

-ba szállított; a harmadik, hogy szintén 3 litert vitt

L

-ből

N

-be; végül az utolsó tag a nap folyamán elfogyasztott víz értékét becsüli meg. Elegendő tehát megmutatnunk, hogy ez az érték nem lehet pozitív, ha

k, l, m, n

olyan nem-negatív mennyiségek, melyekre a (7) feltételek teljesülnek. Kissé átalakítva, a bizonyítandó egyenlőtlenség:

\begin{matrix} {(\frac{5}{3})}^{n} + 2 \cdot {(\frac{5}{3})}^{k} ≦ {(\frac{5}{3})}^{m} + 2 \cdot {(\frac{5}{3})}^{l} + \frac{2}{3} \cdot {(\frac{5}{3})}^{{min}_{}^{} (l, m)} . \end{matrix}

(8)

Ha most

k, l, m, n

megengedett értékein belül

m

-et és

l

-et rögzítve

k

-t és

n

-et egymástól távolítjuk, akkor (8) bal oldala nő. Ezt a távolítást csak akkor nem tudjuk megtenni, ha vagy

k

vagy

n

értéke ,,megakad", azaz

k = m, k = l

, vagy

n = l

valamelyike fennáll.
Legyen

k = m

, akkor (7)-ből

(m + n) ≦ 1 + 2 l

m, n ≧ l

és (8) a következőképpen alakul:

\begin{matrix} {(\frac{5}{3})}^{n} + {(\frac{5}{3})}^{m} ≦ (2 + \frac{2}{3}) {(\frac{5}{3})}^{l} . \end{matrix}

A bal oldal ismét akkor veszi fel legnagyobb értékét, ha

n

és

m

,,távolsága" a legnagyobb, vagyis ha

n

és

m

egyike

l

, a másika

l + 1

. Ezekben az esetekben ez az egyenlőtlenség fennáll.
Ha

k = l

, akkor (7) első egyenlőtlenségéből

n ≦ 1 + m

, a másodikból

k = l ≧ m

, tehát

{min}_{}^{} (l, m) = m

. A bizonyítandó egyenlőtlenség

\begin{matrix} {(\frac{5}{3})}^{n} ≦ {(\frac{5}{3})}^{m} + \frac{2}{3} \cdot {(\frac{5}{3})}^{m} = {(\frac{5}{3})}^{m + 1} \end{matrix}

nyilvánvalóan teljesül. Hasonlóan igazolható (8) abban az esetben is, ha

n = l

. Ez pedig azt jelenti, hogy állításunkat igazoltuk: a feladat végrehajtásához legalább

{(5 / 3)}^{n}

liter vízre szükség van.

Negyedik változat
Láttuk, hogy

{(5 / 3)}^{n}

liter víz mindenképpen szükséges, de az már nem igaz, hogy ennyi elegendő is. Például

n = 1

-re 3 liternél kevesebb nem elég, és

3 > 5 / 3

. Megmutatjuk viszont, hogy

4 \cdot {(5 / 3)}^{n}

liter már elég, még akkor is, ha azt a többletfeltételt szabjuk, hogy

d^{* *}

) az expedíció egyetlen tagja sem ,,ingázhat", azaz mindenki a sivatag egy pontjáig előremegy, ott megfordul, s visszatér a táborba.
Definiáljuk az

a_{1}, a_{2}, ...,

valamint a

b_{1}, b_{2}, ...,

sorozatokat a következőképpen:

a_{1} = b_{1} = 1

; továbbá

i ≧ 1

-re

a_{i + 1}

az a legkisebb egész, amelyre

3 a_{i + 1} ≧ 2 b_{i}

, valamint

b_{i + 1} = a_{i + 1} + b_{i}

. Az alábbi táblázatban a két sorozat kezdő tagjait tüntettük fel:

\begin{matrix} i & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ a_{i} & 1 & 1 & 2 & 3 & 5 & 8 & 14 & 23 & 38 \\ b_{i} & 1 & 2 & 4 & 7 & 12 & 20 & 34 & 57 & 95 \end{matrix}

Lássuk, hogyan tudunk a

d^{* *}

feltétel mellett 1 liter vizet

n

napi járóföldre eljuttatni. Először is indítsunk el

a_{n}

embert tele kulaccsal a sivatagba. Mindannyian nem egészen fél napi járóföldre leteszik a náluk levő 3‐3 liter vizet, s sietve visszafordulnak a táborba, hogy azt még napnyugta előtt elérjék. A táborba visszaérve isszák meg az erre a napra járó 1‐1 liter vizüket. Ezzel majdnem fel napi járóföldre

3 a_{n} ≧ 2 b_{n - 1}

liter vizet juttattunk el. Másnap

a_{n - 1}

embert indítunk teli kulaccsal. Dél felé (nem sokkal előtte) elérik az előző nap otthagyott

2 b_{n - 1}

liter vizet, megisznak belőle összesen

a_{n - 1}

liternyit, majd továbbmennek. Másnap az 1 napi járóföldre levő

P_{1}

ponttól valamivel kevesebb, mint

1 / 4

napi járóföldre mindegyikük leteszi az összes vizét ‐ összesen

3 a_{n - 1} ≧ 2 b_{n - 2}

litert ‐, majd visszafordulnak, s még napnyugta előtt elérik az elsőként telepített ,,tartályt". Ott megisszák a második napi fejadagjukat. Mivel egy napi járásnál kevesebbre vannak a tábortól, a harmadik napra járó vizet már otthon isszák meg.
Ezek után

a_{n - 2}

ember indul útnak. Első nap az első tartályból isznak, második nap a másodikból, s a nap végére elérkeznek

P_{2}

-be. Harmadnap nem egészen

1 / 8

napi járófölddel továbbmennek, ott leteszik a náluk levő

3 a_{n - 2} ≧ 2 b_{n - 2}

liter vizet, s visszafordulnak. Még napnyugta előtt elérik a második tartályt, s a következő nap érkeznek az első tartályhoz, az utolsó napi feladagjukat ők is a táborban kapják meg stb.
Miután az az

a_{2} = 1

darab ember is visszatért a táborba, aki a

P_{n - 2}

ponton túl

1 / 2^{n - 1}

napi járóföldre tette le a nála levő 3 liter vizet, a

P_{0}

és

P_{1}

közti tartályból

2 (a_{n - 1} + a_{n - 2} + ... + a_{2})

liter hiányzik, a

P_{1}

és

P_{2}

közöttiből

2 (a_{n - 2} + a_{n - 3} + ... + a_{2}

liter, a

P_{2}

és

P_{3}

közöttiből

2 (a_{n - 3} + a_{n - 4} + ... + a_{2}

stb. de ezekben a tartályokban eredetileg legalább

2 b_{n - 1}

2 b_{n - 2}

stb. liternyi volt, és

b_{i} = a_{i} + b_{i - 1} + ... + a_{2} + 1

minden

i ≧ 2

-re. Ezért mindegyik tartályban még legalább 2 liter víznek kellett maradnia. Az expedícó utolsó tagja tehát most már eljuttathatja az 1 liter vizet

P_{n}

-be.
Nézzük összesen hány liter vizet használtunk fel. A táborból

a_{n} + a_{n - 1} + ... + a_{2} + 1 = b_{n}

ember indult útnak. Mindegyikük 3 liter vizet vitt magával, s az utolsót kivéve a táborba való visszatéréskor mindegyikük még egy liter vizet ivott. Ez összesen

M_{n} = 4 b_{n} - 1

liter, ezt az értéket kell megbecsülnünk.
Az

a_{i}

számok választása miatt

3 a_{i + 1} ≦ 2 b_{i} + 2

, tehát

\begin{matrix} b_{i + 1} = a_{i + 1} + b_{i} ≦ \frac{5}{3} b_{i} + \frac{2}{3} . \end{matrix}

Ezt az összefüggést ismételten alkalmazva kapjuk, hogy

\begin{matrix} b_{n} ≦ {(\frac{5}{3})}^{n - i} \cdot b_{i} + \frac{2}{3} (1 + \frac{5}{3} + ... + {(\frac{5}{3})}^{n - i - 1}) = {(\frac{5}{3})}^{n - i} (b_{i} + 1) - 1. \end{matrix}

Innen

i = 6

választással kapjuk, hogy

n ≧ 6

esetén

\begin{matrix} M_{n} ≦ {(\frac{5}{3})}^{n} \cdot 4 \cdot {(\frac{3}{5})}^{6} (b_{6} + 1) - 5 ≦ 3,92 \cdot {(\frac{5}{3})}^{n} . \end{matrix}

Ha pedig

n < 6

, akkor közvetlenül is ellenőrizhető, hogy

M_{n} ≦ 4 \cdot {(5 / 3)}^{n}